基于聚合跟踪误差的多USV自适应连续协调控制

张爱华,宋季强,张 洁,杨凌耀

(1.上海工程技术大学 机械与汽车工程学院,上海 201620; 2.江苏省大丰中等专业学校,江苏 盐城 224100)

多无人水面船(Unmanned Surface Vessel,USV)协调跟踪在海洋资源勘探、海上搜救和海底地图绘测方面发挥着巨大的作用[1]。良好的协调编队策略是保证多USV顺利完成任务的关键。目前常见的编队方法有领航者跟随法[2]、基于行为法[3]和虚拟结构法[4]等。其中,领航者跟随法控制结构简单、易于理解和实现,取得了广泛的应用。文献[5]针对USV编队协调控制问题,基于领航者跟随法提出了一种主从编队策略,通过拉格朗日约束函数设计了虚拟约束控制器,完成了路径机动和同步任务。文献[6]为了引导智能体以期望队形机动,基于领航者跟随法提出2层主从结构下高阶多智能体系统的分布式仿射编队机动控制,采用了自适应和反步策略以及分布式估计。文献[7]针对一类离散时变多智能体系统,通过引入虚拟领航者产生期望轨迹,提出一种离散时间迭代学习控制算法。并基于范数理论严格证明了所提出算法的收敛性,仿真验证了该算法的有效性。由于虚拟领航者并非真实存在,可消除实际机器人故障和系统失控的隐患,从而提高了系统稳定性。文献[8]针对多无人机之间的自主协同控制问题,提出一种具有虚拟领航者的优化算法,改进Olfati-Saber模型在实践中的应用,提高了群速收敛速度和系统稳定性,并展示了变速虚拟领航者对复杂无人机分散集群的有效性。

另外,在协调跟踪控制问题中,控制算法的选择十分关键,为了保证控制系统的鲁棒性,滑模控制是很好的选择,但是滑模控制本质是系统滑模面上的切换,会不可避免地产生抖振。为减小抖振对系统的不利影响,文献[9]提出结合滑模控制和主动干扰抑制控制的USV航向角控制器,使用分段函数削弱了传统滑模的抖振现象。文献[10]针对多USV协调跟踪控制,提出了分布式自适应滑模跟踪控制算法以完成对预定轨迹的跟踪。上述方法都致力于改善滑模抖振,但本质上仍是不连续的算法。文献[11]提出一种事件触发滑模控制策略,加入边界层技术,形成了连续控制方法,从而有效降低系统的抖振。文献[12]引入带修正函数的滑模面,提出改进型滑模控制算法,加快系统的收敛速度,减少抖振现象,并利用边界层理论和修正函数构建连续的切换结构,大幅减少系统进入稳定状态的切换频率,可较好地改进USV协调控制系统鲁棒性。此外,文献[13]针对航天器的协调控制,提出了聚合跟踪误差概念,可有效简化协调系统误差模型的复杂度。

基于上述研究,为了解决环境不确定的多USV协调跟踪控制问题,本文针对仅邻近多USV可以通信的无向连通通信拓扑结构,基于领航者跟随编队策略,通过引入虚拟领航者消除实际机器人故障和系统失控的隐患,进而设计所构建的聚合跟踪误差协调控制系统,利用自适应项补偿环境的不确定性,并结合边界层理论提出分布式自适应连续控制算法以提高系统的鲁棒性。基于Lyapunov稳定性理论证明了系统的稳定性,通过仿真验证了算法的有效性。

1 问题描述

定义η=[x,y,ψ]T为USV在大地坐标NOEE中的位置向量,x为北向位置,y为东向位置,ψ∈[0,2π]为艏向角。并定义v=[u,w,r]T为船体坐标系XOY中USV的速度向量,u为纵向速度,w为横向速度,r为转艏角速度。坐标系示意图如图1所示。

图1 坐标系

在本文所研究的协调跟踪控制问题中,假定所有的USV具有相同结构和参数,并用i(i=1,2,…,N)对其进行编号。第i艘USV的数学模型为[5,10]

(1)

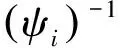
(2)

Mi为惯性参数矩阵,满足Mi>0,Mi定义为

(3)

Ci(vi)为科里奥利力和向心力矩阵,满足Ci(vi)=-Ci(vi),且

(4)

Di(vi)为阻尼参数矩阵,满足Di(vi)vi=Dlvi+Dnvi,其中Di为线性阻尼项,Dn为非线性阻尼项。定义Di(vi)为

(5)

本文针对仅邻近USV可以通信的无向连通通信拓扑结构,定义无向图Ξ来描述USV群体的通信拓扑图,并做出如下假设。

假设1:USV间的通信拓扑图Ξ是无向且连通的。

假设3:第i艘无人水面船的外部干扰di,即‖di‖≤d,式中d>0。

(6)

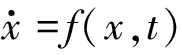
2 基于聚合跟踪误差的分布式自适应连续控制

2.1 聚合跟踪误差的构建

多USV协调轨迹跟踪控制要求无人水面船按照指定的队形协调运动,鉴于领航者跟随编队策略算法设计简单且易于实现的特点,本文采用领航者跟随法实现协调控制中的队形保持。在领航者跟随法应用过程中,若领航者发生故障会导致整个系统瘫痪无法运行,故引入虚拟领航者来提高系统的安全性,并假设仅虚拟领航者已知期望轨迹。

定义群体中各USV相对于虚拟领航者的队形位置和方向向量为li=[xi,yi,ψi]T,其中i=1,2,…,N,并以“0”号作为虚拟领航者的编号,以3艘为例,其位置关系图如图2所示。

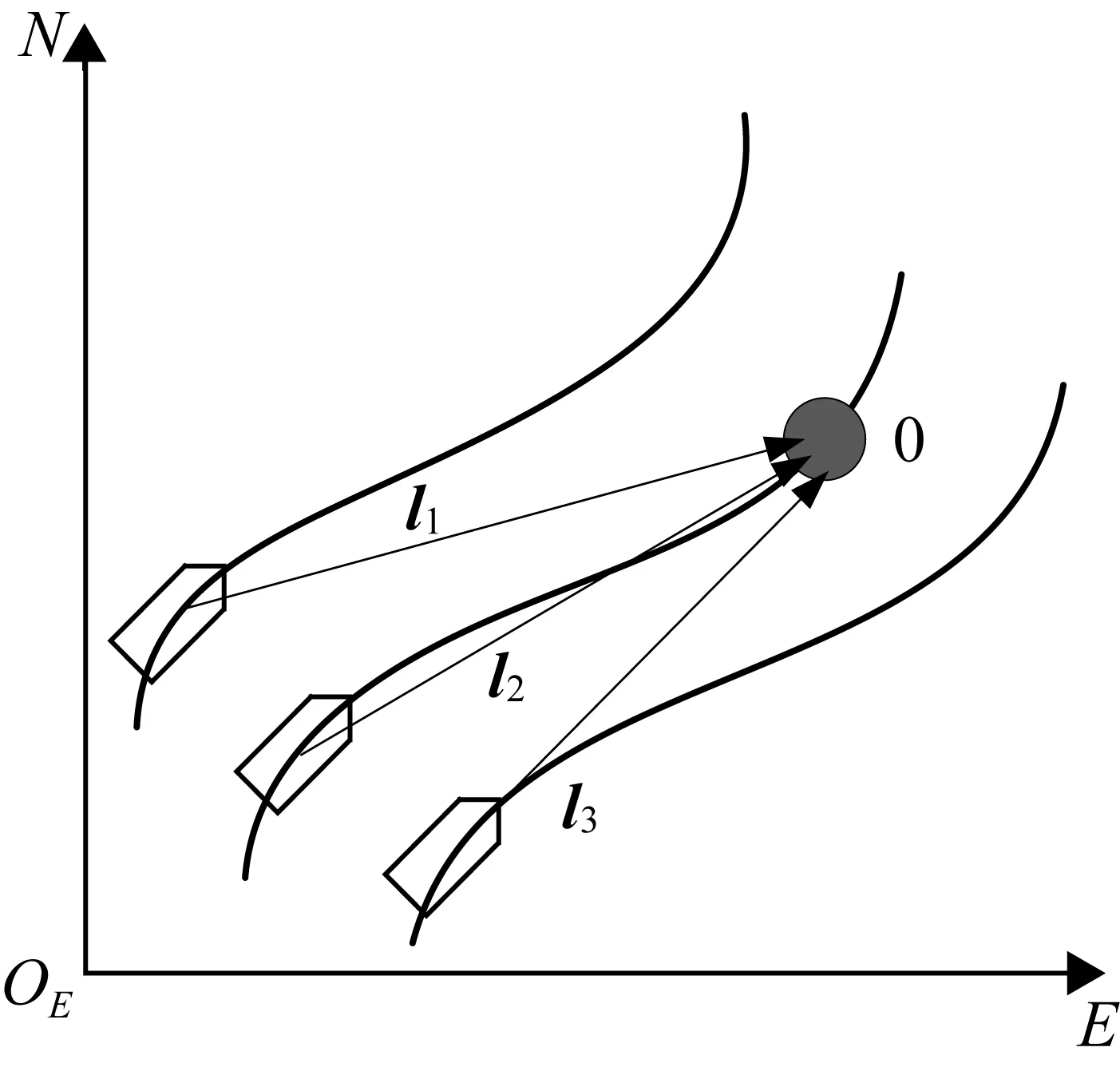
图2 协调跟踪队形示意图

(7)

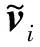
(8)

构造协调聚合跟踪误差,表达式为

(9)

(10)

将式(8)和式(9)带入式(1)可得:

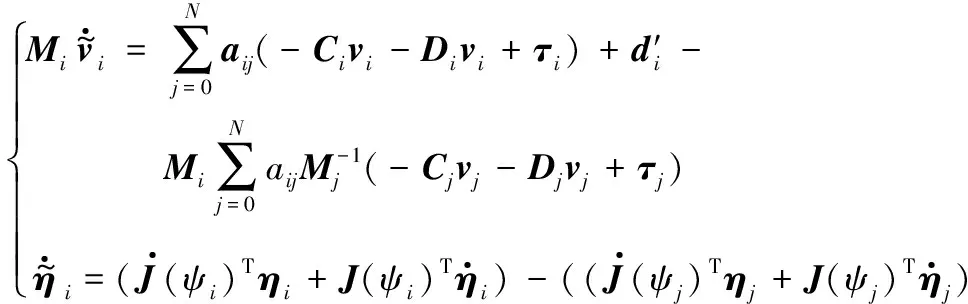
(11)

从而可得到聚合跟踪误差系统的方程为

(12)

其中:

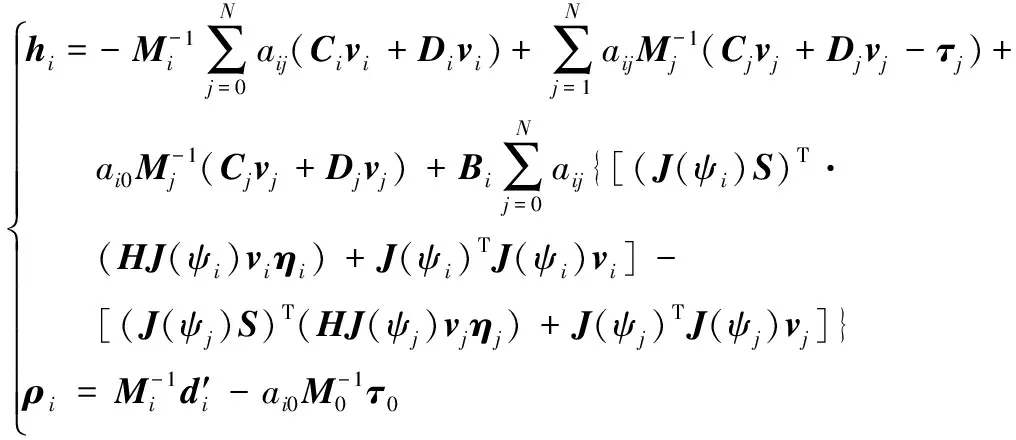
(13)

由假设1和式(13)可知,存在一个正常数,使得‖ρi‖≤φ,i=1,2,…,N。

2.2 分布式连续自适应协调跟踪控制算法及其稳定性

对于多USV协调跟踪控制系统,分布式控制是一个有力的工具,尤其当系统中USV数目较大时,相比于传统的集中控制方式,分布式控制更高效且可节约通信资源。同时考虑到非连续的控制会不可避免地出现抖振现象,本文将结合边界层理论设计连续的分布式自适应控制器。

为协调任务中的每艘USV,设计分布式连续自适应协调跟踪控制器为

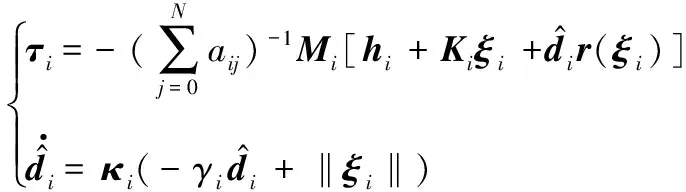
(14)

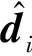
式(14)中,r(•)∈Rn为一非线性连续边界层函数,定义为

(15)

其中,T>0是一个小的正常数,为边界层的厚度。

下面对算法的稳定性进行论证。选取Lyapunov函数为

(16)

沿聚合跟踪误差系统状态对V求导可得:

(17)

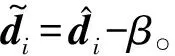
这里分以下3种情况进行讨论。

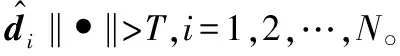
此时有:

(18)

将式(18)代入式(17)可得:

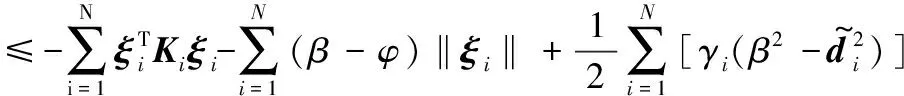
(19)

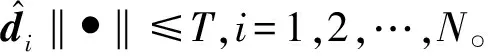
易知此时:

(20)

从而有:

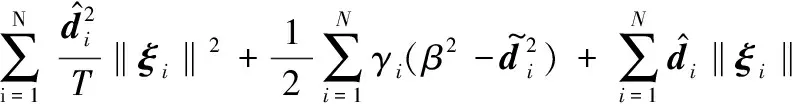
(21)

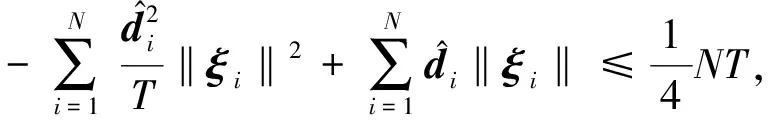
(22)

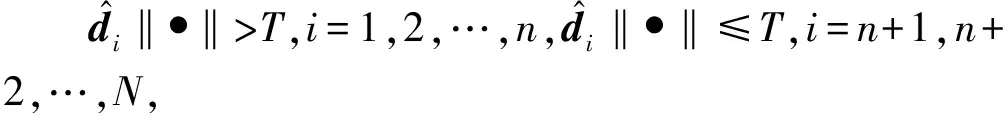
由此可得:

(23)

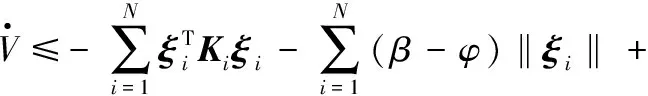
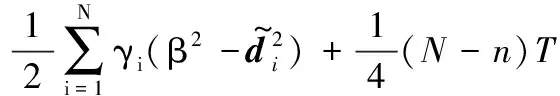
(24)

(25)

3 仿真验证与分析

为验证所提出的分布式连续自适应协调跟踪控制算法的效果,仿真中以3艘USV的协调跟踪控制为例,无人水面船之间的无向通信拓扑图如图3所示,0号为虚拟领航者,1、2、3号为3艘实际USV。

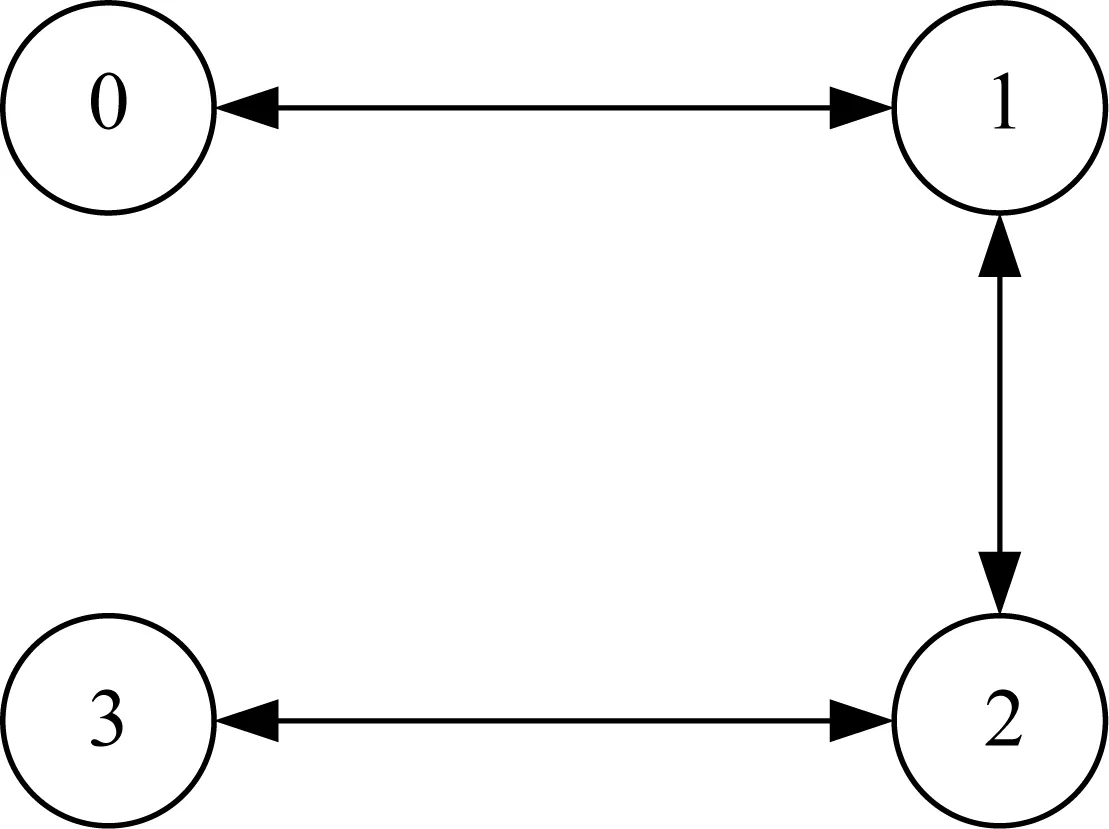
图3 跟随者与虚拟领航者之间的通信拓扑关系

为保证系统稳定性,根据2.2节参数设置要求,仿真参数设置为

T=0.1,κ1=0.01,γ1=0.01,

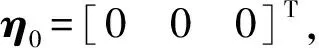
设置参考点与虚拟领航者位置的相对位置向量分别为

基于上述参数,通过MATLAB进行仿真。仿真中各无人水面船跟踪过程中的位置和各状态量的变化如图4～图7所示。

图4 协调轨迹跟踪过程中各USV位置变化曲线

协调跟踪过程中,包括虚拟领航者在内的各USV大地坐标中位置变换曲线如图4所示。由图4可以看出,在所提出的协调跟踪控制算法作用下,USV群组完成了设定的协调跟踪控制任务,在跟踪之初,各USV迅速调整位置,以设定队形完成了对期望轨迹的跟踪。

协调跟踪过程中各USV的速度变化曲线如图5所示,图5(a)～图5(c)分别为各USV纵向速度、横向速度和艏向角速度的变化曲线,可以看到在所提出的连续控制器的作用下,各USV的速度波动较小,响应速度快,运动平稳,最终速度一致。各USV协调跟踪过程中聚合跟踪误差变化曲线如图6所示,图6(a)～图6(c)分别为各USV纵向、横向和艏向角的聚合跟踪误差变化曲线,显然聚合跟踪误差保持在零点附近的小范围内且有界。各USV对应的协调跟踪控制量的变化曲线如图7所示,图7(a)～图7(c)分别为各USV纵向控制力、横向控制力和艏向控制力矩变化曲线,可以看出所提出的分布式连续控制算法得到的控制输出平滑,系统具有良好的鲁棒性,这不仅有利于提高控制系统的精确度,而且能够延长控制器的寿命、减少控制器能量的损耗。

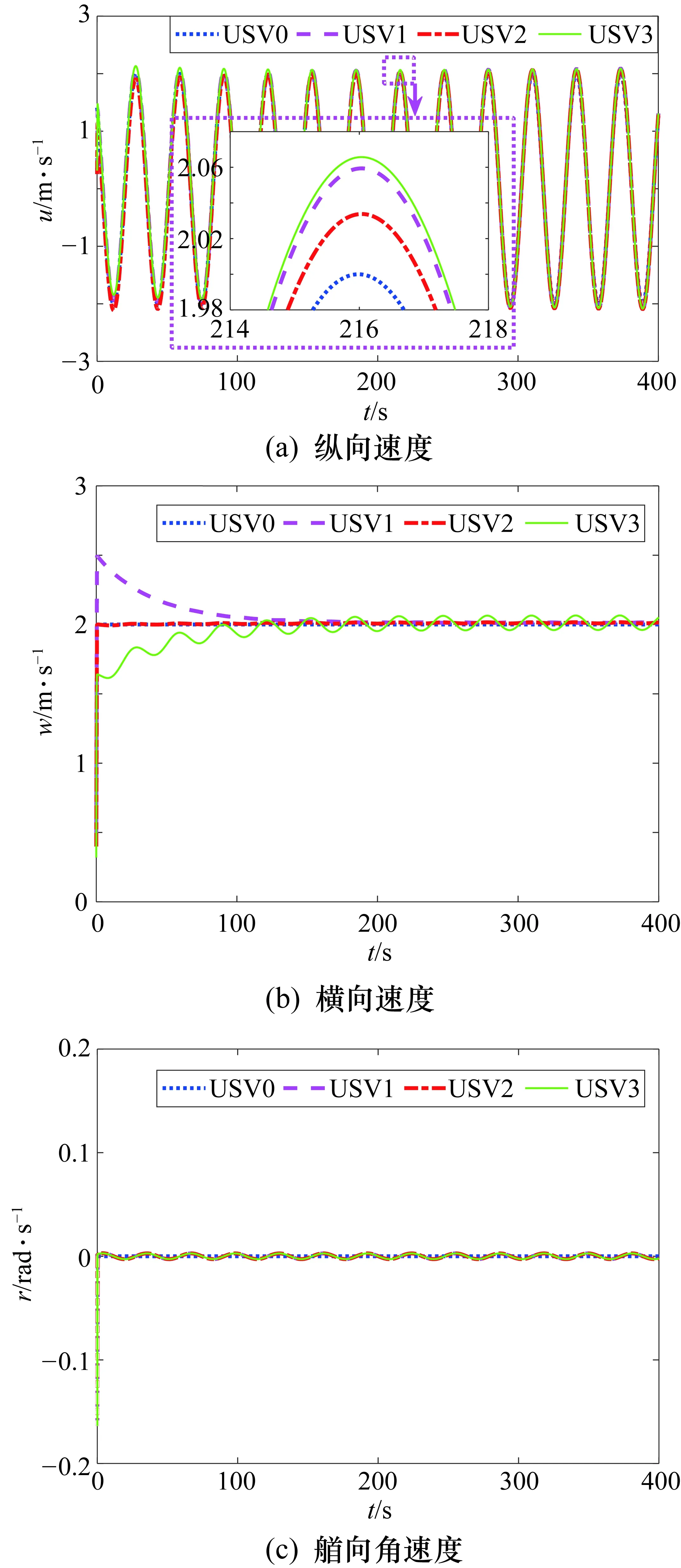
图5 协调跟踪过程中的USV速度曲线

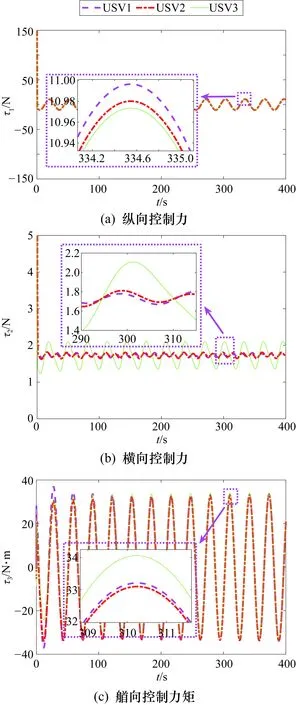
图7 各USV协调跟踪控制量的变化曲线

此外,需要指出的是,本文提出的算法是连续的,与笔者团队在文献[10]中提出的非连续控制器相比,有效避免了抖振问题,而且从理论证明和仿真结果中都可以看出,本文提出的算法使聚合跟踪误差是毕竟有界的。

4 结束语

针对多USV协调跟踪控制问题提出了一种分布式连续自适应协调控制算法,该算法引入了虚拟领航者,基于聚合跟踪误差为协调控制的各USV设计分布式连续自适应协调跟踪器,并通过自适应项实时调节控制器参数抵御外界干扰,理论证明了协调控制系统的稳定性,并通过仿真验证了所提出的算法具有良好的控制效果,有效保证了系统的鲁棒性,避免了控制输出抖振,可延长控制器的寿命、减少控制器能量的损耗。

本文所提出的分布式自适应连续协调跟踪控制算法虽然有效避免了控制量的抖振,但牺牲了部分控制效果,也就是只能保证聚合跟踪误差和自适应误差收敛到零点附近的小邻域内,因此,如何通过对比分析进一步提高系统的稳定性和鲁棒性是下一阶段的研究目标。