非常规油气田开发作业废液处理站选址模型研究
2023-11-07王江力张树德王占生
王江力 张树德 王占生 兰 军 邵 斌 贺 美
(1.中国石油集团安全环保技术研究院有限公司;2.长江大学资源与环境学院;3.长庆实业集团有限公司)
0 引 言
目前国内关于选址研究集中于运筹学和地理信息系统分析两个领域,其中运筹学领域是利用已经封装好的数学模型程序,如小规模求解使用CPLEX[1-2]、Gurobi[3-4]、Lingo[2]求解器,较大规模可使用Matbal等软件,并利用已有的选址模型[5],通过调整部分参数来解决选址问题,而地理信息系统分析领域主要是利用Arcgis软件对影响选址的地理因素、政策因素及环境影响因素进行系统分析[6-7],从而找出最优的选址区域。
在城市污水处理厂选址过程中,主要考虑水文地质、综合风向、城市管网等因素,采用近似指标权重和多目标优化方法对城镇污水处理厂进行选址优化分析[8-9]。非常规油气开发作业废液处理站服务于井场区域,主要的选址方法有重心法、最大最小化方法和多目标优化平面选址等方法[10],然而每种方法都只适用一种情景模式。例如,华北某气田在确定备选点位置及废液运输路径情况下,采用选址—路径模型,利用遗传算法合理规划出污水处理厂选址位置[11]。国内对非常规油气田作业废液处理站选址主要通过专家论证来确定作业废液处理站位置,缺乏处理站选址经济性的理论支持。本文以经济效益最大化为目标,从编码的原始角度,根据现有数据构建废液处理站选址模型,利用Python-jupyter notebook编程并对数据进行分析,解决非常规油气开发作业废液处理站选址的经济性问题。
1 选址模型建立与运行
1.1 问题描述
随着非常规油气田的大力开发,产生的大量作业废液大都运往井场作业废液处理站进行集中处理,处理后的作业废液重新回注到注水井中,作业废液从产生到处置全过程物流网络模型见图1。
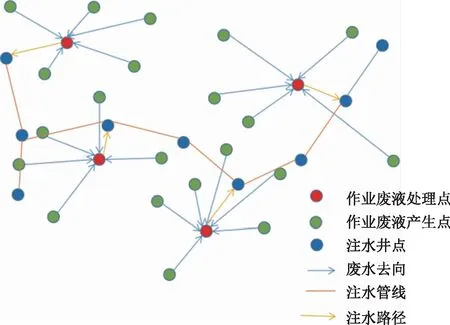
图1 作业废液处置全过程物流网络模型
作业废液处置全过程物流网络包括作业废液产生点、作业废液处理站及注水井。因此作业废液处理站的选址是非常规油气田开发和运行成本的重要影响因素之一。
1.2 选址模型条件假设
为了方便建立数学模型,利用Arcgis、Excel软件,结合研究区域地理、井口坐标、单井废液产量等信息来划分井区并将其合并为一个井位节点,缩小数据处理的数量,使选址模型更具实用性,需要对模型作以下假设:
1)按照井场井口分布从密集区域到离散区域划分井位节点,取密集区域中心点作为基准点,将方圆1 000 m内的油气井合并为一个井位节点。在该节点外1 000~3 000 m若存在一个或两个单独油气井,可将其合并入该井位节点中。在离散区域中,则将间距小于3 000 m的离散油气井作为一个井位节点,如果大于3 000 m的离散油气井则直接作为一个井位节点。
2)作业废液总量确定,且单日最大废水产量已知。废液处理遵循就近原则,处理站选址位置靠近废液产量大的井位节点。
3)作业废液处理站处理规模限定在一定范围内,分别为300,500,800 m3/d。
4)废水回用全部以管道输送形式回注到周围的注水井。
5)处理站的建立不会加重该区域环境污染,选址点的位置应远离水域环境,符合当地政策和法规。
根据目标函数和约束条件构建一个非常规油气开发作业废液处理站选址的数学模型,见公式(1)~(4)。
目标函数:
(1)
约束条件:
(2)
(3)
(4)
决策变量:
模型参数定义如下:
i为油气田井口点下标,i=1,2,3…i;j为废水处理站点下标,j=1,2,3…j;Ai为废水产生点i产生的废水总量,m3;Fjk为在j点建设k型设施的建设费用,元;k为作业废液处理站日处理量,m3/d;N为处理站类型的集合;W为作业废液的运输费用,元;Lij为第i个废水产生点到第j个废水处理站的距离,km;Cjk为j点k型处理站的单日处理量,m3/d;ε为单日产水系数;Q为总成本,元。
其中目标函数(1)的两部分分别表示设施的建设费用、废水的运输费用;约束条件(2)表示一个废水产生节点只能运往一个废水处理站;(3)表示设施的数量为p;(4)表示运往处理站的单日水量要小于处理站的处理量。决策变量Xjk与Yij,其中Xjk=1表示在备选点j建立k型废水处理站,Xjk=0表示不在j点建立k型废水处理站;Yij=1表示需求点i送往废水处理站j点,Yij=0表示需求点i未被送往处理站j点。
1.3 数据预处理
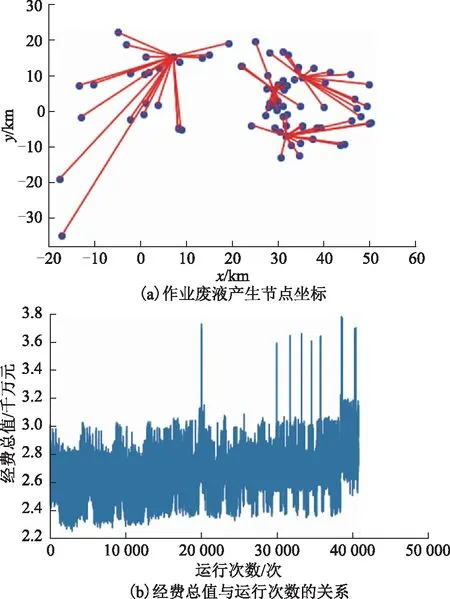
将长庆油田某采油厂611口油气井按照条件假设要求合并成83个井位节点,废水总量为255 828 m3,节点位置分布见图2。
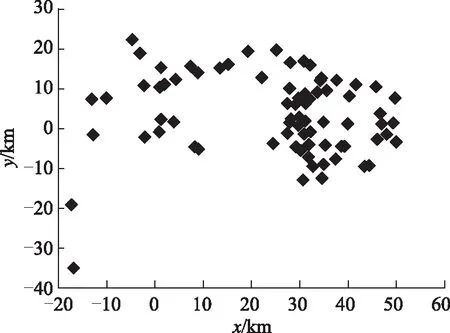
图2 作业废液产生节点
运输过程是模型计算中的一个重要部分,不同的运输价格对模型产生的影响不同,本文根据某采油厂压裂返排液运输队伍框架协议招标公告,结算单价按照如表1价格区间执行。
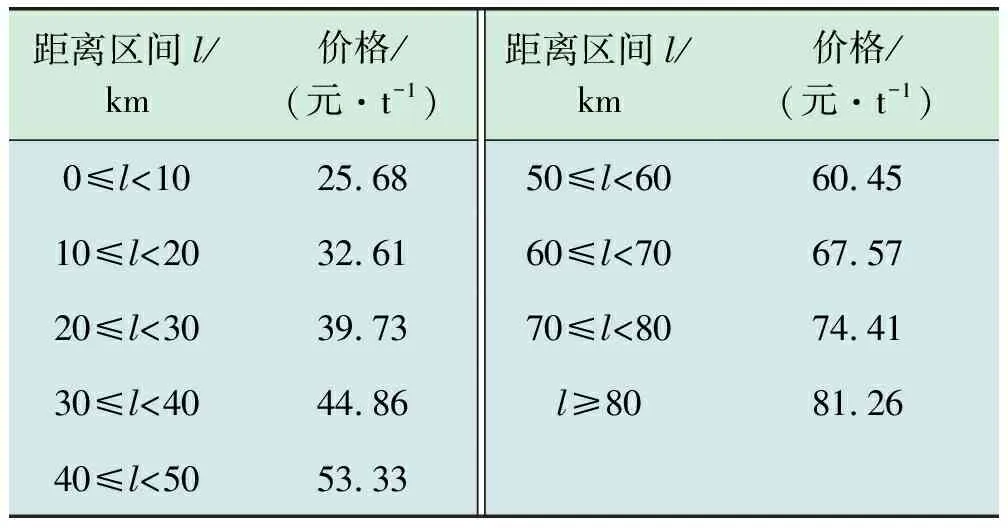
表1 不同距离区间的运费价格
1.4 路径修正
二维平面中有两种路径可供选择,分别为欧式距离与曼哈顿距离,见公式(5)~(6)。
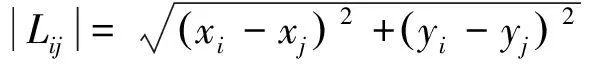
(5)
(曼哈顿距离)|Lij|=|xi-xj|+|yi-yj|
(6)
其中欧式距离表示两点之间的直线距离,而曼哈顿距离表示固定直角坐标系上两点所形成的线段对轴产生投影距离的总和。但对于实际距离而言,这两者都存在明显的误差,且误差为不可控因素,因此需要在原有距离的基础上添加修正因子。关于路径修正因子已有相关研究,在曼哈顿距离的基础上,道路的平均距离与道路的等级具有一定的相关性,利用赋权法和道路的等级效应便可得到相应的修正参数[12]。欧式距离在二维平面上的修正距离未有具体介绍,但是在二维平面上的离散点修正早有研究,主要体现在二维平面上自变量和因变量关系来构建线性回归函数,利用损失函数来确定回归函数的准确性。将这种线性规划运用到欧式距离路径优化上,可将直线距离看成自变量,路径距离看成因变量,做出相应的线性回归方程,对路径做出相应的修正。
1.5 模型运行模式
本文主要运用Jupyter Notebook基本的for循环工具,加上该工具中自带的功能包,如numpy、pandas、random等构建需要的选址相关函数,其主要操作分为4步,分别为:
1)导入工具包。主要工具包包含随机数模块(random),矢量化的计算模块(numpy),数据分析模块(pandas),对角化模块(itertools)以及距离计算模块(scipy. spatial.distance)。
2)构建函数。需要依据选址数学模型特征构建所需函数,主要的函数包括数据组合函数、两点之间的距离函数、选址函数、0~a分配函数(最小值不变,其他值为0)、0~1分配函数(最小值为1,其他值不变)、对角矩阵函数、约束函数等。
3)函数的运用。首先利用数据组合函数与两点之间的距离函数,通过for循环可以得到若干选址函数,再将选址函数进行0~a和0~1分配操作,得到0~a分配函数和0~1分配函数,再将0~a分配函数和0~1分配函数与废水产量的对角函数结合,便可得到约束函数、废液运输费用、处理厂建设费用,通过循环若干次后,得到每种选址组合的经费总价。最后用列表将所有选址组合的经费总价汇集,找到经费总价的最小值。
2 结果与讨论
1)路径优化结果
根据1.4对两种距离的介绍,在非常规油气开发区域,曼哈顿距离与欧式距离在应用中都存在误差,需要通过相应的路径修正方法来达到目标要求,但是在数据收集与路径优化过程中,曼哈顿距离的优化方式可能更加复杂,因此选择欧式距离来表达选址过程中的距离函数可能更加合适。在得知直线距离与路径距离有明显的线性相关性,但又存在较大不稳定性的前提下,选择欧式距离作为两点之间的直线距离,做出相应的线性回归方程和多项式Y=wX+b、y=4E-0.6x5-0.000 5x4+0.028x3-0.658 6x2+7.976 1x-7.484,结果见图3。其中w=1.430 3,b=12.789,E=10-6,线性回归的准确性在76.6%,多项式的准确性达77.9%,两种方式准确性相差较小,但多项式存在过拟合情况,而线性回归符合现实情况。当直线距离等于0时,线性回归的路径距离达到12.789 km,因此需要对直线距离小于10 km的这一区间进行重新定义。利用线性关系做出相应的线性函数(如图4所示),发现其线性相关性不大,因此在0~10 km不能使用线性函数表达。
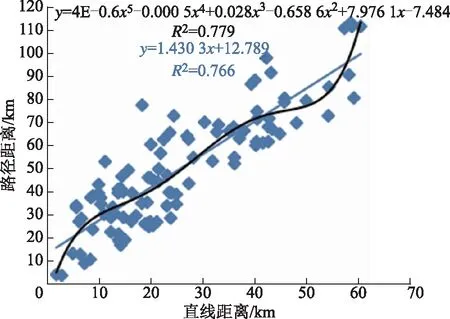
图3 直线距离为0~80 km的修正路径
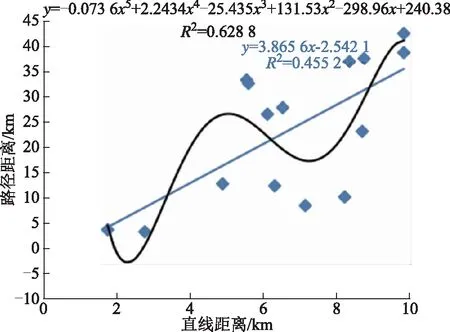
图4 直线距离为0~10 km的修正路径
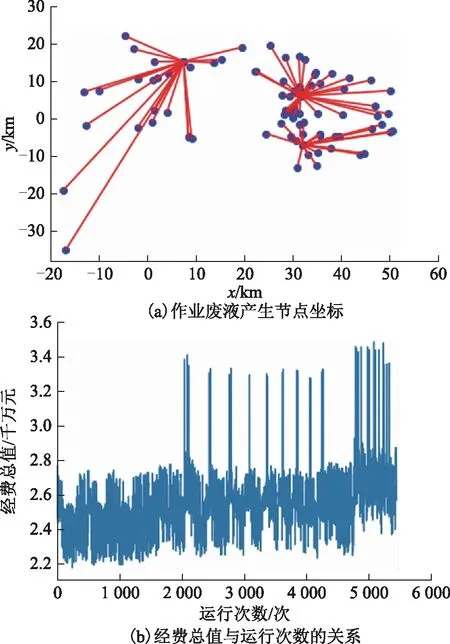
由于开发区域在野外、林区、山区、荒漠等地,所以有些直线距离很近的区域,其路径距离可能很远,根据点位分布可以发现当直线距离小于4 km时,路径距离变化幅度较小,当直线距离大于4 km小于10 km时,路径距离变化幅度较大,没有规律性。因此利用概率分布来表示4~10 km的路径距离,即P(x<10)=8.4%,P(10 (7) 其中f(x)为距离优化函数,g(x)表示4~10 km对应路径距离的概率分布随机数。 2)模型运行结果 图5 单座处理站选址 通过改变废液处理站数量p值来选择合适的选址方案,井位节点单日最大产废液量1 015 m3/d,井区废液总量为255 828 m3。当p=1时,单座处理站选址见图5,经过模型运算后确定处理站选址坐标为(31.192,8.488),当模型运算到第11次后经费总价出现最小值2 193.09万元,运输费用高达1 093.09万元。 当p=2时,两座处理站选址见图6,选址坐标为(7.364,15.247),(31.192,8.488),当模型运行到10次时经费总价出现最小值2 038.24万元,其中处理站规模分别为300,800 m3/d,运输费用分别为276.84,661.40万元。 图6 两座处理站选址 当p=3时,3座处理站选址见图7,选址坐标为(7.364,15.247),(31.488,5.98),(31.93,-7.188),当模型运行到238次时经费总价出现最小值2 108.96万元,其中处理站规模分别为2座300 m3/d、1座500 m3/d,运输费用分别为274.01,165.28,469.67万元。 图7 3座处理站选址 当p=4时,4座处理站选址见图8,选址坐标为(7.364,15.247),(29.194,5.898),(35.447,9.427),(31.93,-7.188),当程序运行到2 903次时得到经费总价最小值2 248.69万元,4座处理站规模均为300 m3/d,运输费用分别为288.70,184.15,206.80,169.04万元。 图8 4座处理站选址 上述选址模型运算结果显示,随着作业废液处理站数量增加,运输费用逐渐降低,即选用单座作业废液处理站时,运输费用最高,选用4座作业废液处理站时,运输费用最低。 在非常规油气田开发过程中,作业废液的有效处置是重要一环,合理确定作业废液处理站位置对降低油气田开发成本具有重要意义。本文基于经济效益最大化为目标函数,应用Arcgis、Excel、Python软件工具,构建一个经济效益最大化的选址模型,该模型并不局限于建设设施费用最小或运输距离权重最小等单一因要素,而是综合考虑全过程经济费用最小。通过对非常规油气田开发作业废液处理站选址模型的初步研究,得出以下结论。 1)基于建站费用与运输费用之和最小的经济效益最大化为目标函数可以构建非常规油气田开发作业废液处理站选址模型,该模型可用于指导废液处理站的选址,但经济效益影响因素还需要进一步优化。 2)对井场井位数适度合并后,可选用穷举法进行数据分析得出废液处理站适宜的坐标位置,但需要优化模型及Python编码的算法,使作业废液处理站选址模型向数字智能化转型。 3)由于非常规油气田大多采用循序开发,井位节点不断前移,宜考虑建立多点可移动式作业废液处理站,以降低建站费用。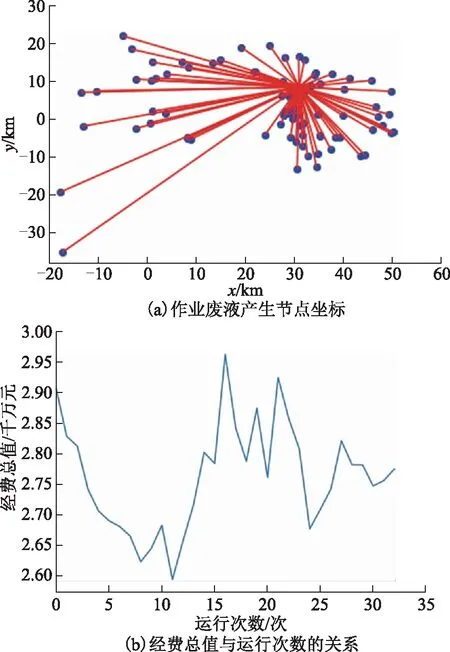

3 结论与展望
