基于核熵成分分析的工业过程故障诊断

李 榕, 李 元

(沈阳化工大学 信息工程学院, 辽宁 沈阳 110142)

随着工业生产过程越来越复杂多变,生产过程中对于设备的安全性和可靠性要求也愈加严格[1-2]。为了更多地捕捉过程信息,往往安装多样的传感器来获取大量反映过程信息的数据。通过分析正常数据和不同故障运行模式下的数据,实现基于数据驱动的故障诊断[3-5]。

工业过程数据往往具有维数高、复杂性强等特点,若直接对获取的原始数据进行故障诊断,不仅消耗计算机资源多,而且诊断效果较差,因此,在工业过程数据上,对原始数据首先进行降维处理,去除数据冗余信息、压缩数据维度从而减少存储空间,消除数据噪声进而提高分类器的分类准确度。主成分分析(principal component analysis, PCA)[6]作为工业过程数据中最经典的降维方法,能够处理高维、嘈杂和高度相关的数据,因其优异的表现而被广泛应用于故障诊断领域。陈辉等[7]为了解决在设备故障分类识别中易受输入样本相关性影响的问题,提出PCA-BP神经网络方法对设备进行故障预测。张弛等[8]提出主成分分析和优化参数支持向量机的智能变电站故障诊断模型,用以解决目前智能变电站故障诊断结构复杂、样本数据量小的问题。但是,当数据分布具有非高斯和非线性特征时,由于使用二阶统计量和线性假设,PCA此时表现不佳。核主成分分析(kernel principal component analysis, KPCA)[9-11]在一定程度拓宽了PCA的应用范畴,利用非线性映射将输入数据映射到高维特征空间,在特征空间执行PCA。李梦瑶等[12]用KPCA降低数据维度、剔除冗余信息,从而实现齿轮箱的故障诊断。武文栋等[13]提出KPCA结合麻雀搜索算法优化核极限学习机的方法,用以提高光伏阵列故障诊断的精度。然而,在实际工业过程中,数据通常同时存在着高斯分布和非高斯分布特性,而KPCA在选取主成分的过程中只使用过程变量的方差信息,因此缺少处理非高斯数据的能力,对一些复杂的系统故障处理效果也就不理想。

2010年,Jenssen[14]提出一种新的降维方法——核熵成分分析方法(kernel entropy component analysis, KECA)。对比KPCA只考虑方差信息只能提取数据的高斯特征。KECA[15-17]以信息熵为信息衡量的指标,使用高阶统计量最大程度保留原始数据的熵值,同时,其能够捕捉到数据内部的结构信息。如今,KECA在干旱监测、柴油机故障识别、风电功率预测等领域被广泛应用[18-20]。但目前未查到该方法在化工工业过程多类型故障诊断领域的应用。

针对传统算法在多类型故障诊断率较低的问题,本文提出一种KECA-CSK的故障诊断方法。KECA进行多种数据分析时,不同类别的数据样本往往互相垂直,而同一类别的数据样本往往共线,基于此特点设计一种基于余弦相似度的K均值聚类器,建立诊断模型,从而对未知类型的故障数据进行判别。本文对田纳西-伊斯曼化工过程(Tennessee-Eastman,TE)进行模拟实验,验证KECA-CSK均值方法在故障诊断领域的有效性。

1 故障诊断方法

1.1 核熵成分分析方法

定义数据集D={x1,x1,…,xn}的概率密度函数p(x),其Renyi熵H(p)表示为

(1)

由式(1)可以看出,Renyi熵估计取决于数据集的概率密度函数,不需要对数据的分布进行限定,算法的适用性更强。因为对数函数本身具有单调性,因此只需考虑

(2)

(3)

(4)

式中:K为n×n的核矩阵;I为n×1的单位向量。核矩阵包含了二次Renyi熵估计值所需的所有元素。对核矩阵进行特征分解,

K=EΛET。

(5)

式中:Λ=diag(λ1,λ2,…,λn)表示特征值矩阵;E=(e1,e2,…,en)表示特征向量矩阵。将式(5)代入式(4),得到

(6)

由式(6)可得,Renyi熵可以表示为n个分量的累积,各个分量都同时包含特征值与特征向量。

将输入数据集D={x1,x2,…,xn},通过非线性φ映射到核特征空间定义为xi→φ(xi)(i=1,2,…,n),该特征空间的数据可表示为Φ=[φ(x1),φ(x2),…,φ(xn)]。由于KECA可以被看作最大限度地保留Renyi熵估计的主轴在包含原始数据最多信息的情况下构造成的子空间,即将数据映射到由k个KPCA主轴张成的子空间Uk上,对ζi值从大到小排序,选取前k个特征值和特征向量,转换后的数据表示为

(7)

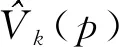
对于新的样本xnew在Uk上的投影可表示为

(8)

1.2 CSK方法

K均值算法由于其原理简单、易于理解、容易实现以及理论可靠等优点而被广泛应用于不同领域。由于TE数据经KECA特征提取后不同类的数据分布在不同的角度方向上,因此本文使用样本到各个质心的夹角余弦值来衡量数据样本之间的相似性,即余弦值越大,表明数据与该类别的数据样本相似度越高。

假设两个包含m维特征的向量,表示为α=(a1,a2,…,am),b=(b1,b2,…,bm),则夹角余弦值可表示为

(9)

当α,b方向一致时,数据之间夹角越小,夹角余弦值就越接近于1,数据相似度也就越高;同理,当两者之间夹角越大,夹角余弦值就越小,数据相似度也就越低。

基于CSK的方法步骤如下:

1) 初始质心的确定。选取余弦相似度最低的数据样本作为前2个初始质心,然后再选择与前2个初始质心余弦相似度最低的数据样本作为第3个初始质心,以此类推,直至确定C个初始质心;

2) 将数据样本划分到与C个初始质心余弦相似度最高的类别中;

3) 更新每个数据类别中的类质心;

4) 重复步骤(2)～(3), 当质心位置变化小于给定的阈值,循环结束,保留各类别中心。

CSK均值方法运用于故障诊断领域,首先是将混合的不同故障类别数据进行聚类,聚类结束以后,保留不同故障类别的聚类中心,构建诊断模型。对新获得的未知类别的测试数据进行故障诊断时,确定此故障数据样本与哪一类别的聚类中心余弦值最大,那么该样本的故障类别属性就与那一类故障样本的类别属性一致。

1.3 KECA中核参数的选取

本文KECA中核函数选取高斯核函数,表达式为

k(x,xt)=exp(-0.5||x-xt||2/δ2)。

(10)

式中,δ为待优化的核参数。

在聚类分析中,尽可能使得同类数据之间相互靠近,不同类数据之间相互远离。因此,核参数选取规则定义如下:

1) 类内离散度。

(11)

2) 类间离散度。

(12)

式中,C为数据样本类别个数。

使用基于角结构的类内与类间离散度的差作为选取的准则函数,即:

(13)

根据Shi等[21]提出的参数值选取方法,将原始空间样本欧氏距离中值的10%～20%作为参数选取范围,然后利用所定义的准则函数选取合适的核参数。

2 基于KECA-CSK均值故障诊断

基于KECA-CSK均值故障诊断方法分为离线建模和在线诊断2部分,KECA-CSK均值方法的诊断流程图如图1所示。

2.1 离线建模

1) 获取训练数据共m个变量n个样本X=[x1,x2,…,xn]∈Rm×n,并进行标准化处理;

2) 构建KECA模型,根据式(7)计算得分矩阵Feca;

3) 计算Feca向量之间的余弦值,确定C个初始聚类中心;

4) 根据余弦相似度大小,将数据划分到相对应的类群中;

5) 更新C个类群的聚类中心;

6) 重复步骤4)～5),各类群中心变化小于阈值,则停止,获得聚类中心。

2.2 在线诊断

1) 测试数据xnew并进行标准化处理;

2) 测试数据向KECA模型进行投影,通过式(8)计算得分矩阵Fknew;

3) 计算Fknew与建模时各类群聚类中心的余弦值,将其划为余弦值最大的类群。

3 TE仿真实验

TE过程是由美国Eastman化学公司的Downs和Vogel共同开发的TE Benchmark仿真模拟平台,由该平台产生TE数据,近年来被广泛应用于工业生产故障检测与诊断[22-26]。TE工业流程主要包括反应器、冷凝器、循环压缩机、气液分离器和汽提塔等5个操作单元,整个过程中共涉及8种物料成分,分别为主要参加反应的气体进料U、C、D、E;惰性不可溶进料B;反应副产品F以及反应液态主产物G和H。该平台总共预设了21种故障,其中,IDV1～IDV7为阶跃故障,IDV8～IDV12为随机变化故障,IDV13为慢偏移故障,IDV14～IDV15为堵塞干扰故障,IDV16～IDV21为未知型故障。

3.1 样本选取

本文选取TE过程故障1、故障5和故障18作为研究对象。故障具体描述如表1所示。在训练集中,正常数据样本是在25 h 运行仿真下获得,样本总数为500;故障数据样本是在24 h运行仿真下获得,样本总数为480。本文选取训练集3×400×52,其中3是3类故障类型,400是数据样本个数,52是变量数。在测试集中,正常数据样本是在48 h运行仿真下获得,采样间隔时间为3 min,样本总数为960;故障数据样本是在48 h运行仿真下获得,故障在8 h的时候引入,样本总数为960,其中,前160个数据样本为正常数据样本。本文选取测试集为3×400×52。

表1 故障数据描述Table 1 Fault data description

3.2 故障诊断

3.2.1 核参数确定

以TE过程为背景进行仿真实验,训练数据选取故障类型1、5和18共1 200个数据样本,测试数据为同样的未知标签的3类数据共1 200个数据样本。经计算,原始空间样本欧氏距离中值为50.015,核参数的选择区间为δ=50.015×u,u=0.1∶0.01∶0.2,利用准则函数选取合适的核参数,核参数的取值与准则函数值的关系如图2所示。为了便于可视化以及诊断分析,同时确定k、l为聚类数3。

图2 不同核参数下的准则函数值Fig.2 Criterion function values under different kernel parameters

观察图2可得,当核参数取欧氏距离中值的17%时,准则函数最大,因此本实验中核参数取值为8.502 55。

3.2.2 实验分析

为了验证KPCA(KPCA中核参数的取值方式与KECA取值方式一致)与KECA之间的差异性,将所建立的核矩阵分解后,得到特征值和Renyi熵值,并将其归一化,如图3(a)所示,KPCA依据特征值大小选取第1、2、3主成分,KECA中基于Renyi熵值贡献选取第1、2、6主成分,即特征值大的不一定取得Renyi熵值贡献也大。根据KPCA与KECA两种方法选择各自不同的主成分后将数据进行投影,如图3(b)和3(c),KPCA投影将3类数据分开后,数据分布较为分散,也没有出现明显的角结构特性,而KECA分析中,数据之间具有明显的角结构特征,数据分布较为紧密,有利于CSK方法对数据进行聚类。

图3 3种故障聚类实验分析Fig.3 Analysis of three fault clustering experiments

对核矩阵的第1、2、3和6特征向量进行分析,如图4所示。

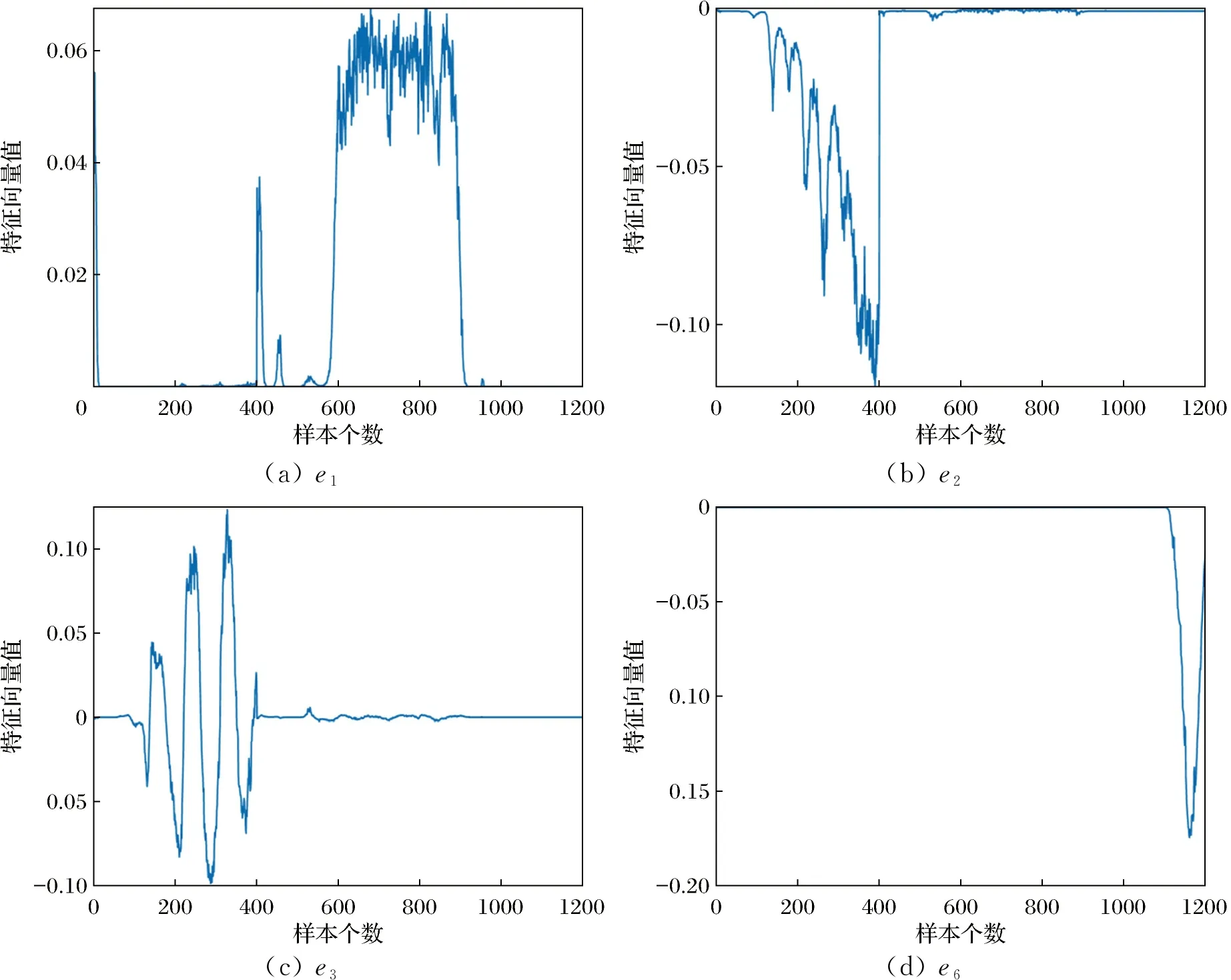
图4 训练数据核主成分Fig.4 Kernel principal components of training data

观察图4可得,KECA根据Renyi熵贡献大小,选择第e1、e2、e6特征向量。e1、e2、e6特征向量中均有一段对应于其中一个数据类别的正值或负值,而对于其他类别值均接近于零,即KECA所选取的特征向量携带数据集的簇结构信息,因此,转换数据集的角结构也将会出现,如图4(c)所示。对于e3特征向量,其在零附近上下波动,对于Renyi熵贡献也基本为0,KECA按照Renyi熵值大小也就不会选取该特征向量作为投影方向。KPCA对数据特征提取时,根据特征值降序排列选取e1、e2、e3特征向量。然而,e3特征向量分布没有刻画出故障18的数据的特点,不能获取数据的结构信息。因此,对比KPCA方法,KECA能够提取不同类数据的差异性,获取数据内部存在的结构信息,使得转换后的数据保持较好的可区分性。

3.2.3 训练数据聚类

基于上述分析后,使用本文所提出的CSK聚类器,对训练数据进行聚类,获取各类群的聚类中心,聚类结果如图5所示。

图5 聚类结果Fig.5 Clustering result plot

图5(a)是训练数据KECA-CSK聚类结果,3种类型样本的聚类正确率分别为95.5%,96.0%和35.0%。图5(b)是KPCA的聚类结果,3种故障类型数据样本的聚类正确率分别为89.25%,54.25%和28.00%。KPCA聚类效果相比KECA聚类效果较差。训练数据聚类结果的正确率直接影响对未知类别故障数据的诊断正确率。

3.2.4 未知类别的故障数据诊断

对于包含与建模数据相同的测试样本,将其投影到建模模型获得得分向量,计算得分向量与建模结果中各类群中心的余弦值,将其划为余弦值最大的那一类别中。若测试数据的故障类型不同于建模数据的故障类型时,将其代入其他数据建立的诊断模型中,图6是KECA与KPCA的诊断结果。

图6 故障诊断结果Fig.6 Troubleshooting results

图6(a)是KECA的诊断结果, 3种未知故障类型的测试数据样本基本均能得到有效判别, 总数据样本的诊断正确率为80.08%。 KECA特征提取时候, 捕捉到的数据集群结构信息使得CSK方法在训练数据上能够取得较好的聚类结果, 进而影响对测试数据的诊断结果。 图6(b)是KPCA诊断结果, 诊断结果较差, 总数据样本的诊断正确率为59.08%, 验证了KECA在工业过程故障诊断领域的优越性。

4 结 论

针对实际工业过程中,传统核主成分多故障类型诊断率低问题,本文提出一种基于KECA-CSK均值的故障诊断方法,并在TE化工过程数据取得较好的诊断效果。KECA对数据进行特征提取,转换后的数据不同类别数据之间保持角结构特性,在此基础上设计一种基于余弦相似度的K均值聚类方法,从而获得较高准确率的建模结果,提高对未知类型数据判别的正确率。 后续工作集中于探究该方法在其他工业过程的应用是否也能取得较好的诊断结果。