基于IGDT和PSO-SA的综合能源系统鲁棒优化调度方法

彭宇文，李瑞，周永旺，李沁雪，尚筱雅，蔡政彤，许灿城

(1.广东工业大学 自动化学院，广东 广州 510006；2.广州航海学院 船舶与海洋工程学院，广东 广州 510700)

随着现阶段电力需求的增加，环境污染所引发的生态问题受到国内外学者们的广泛关注[1]。综合能源系统(integrated energy system，IES)的优势在于它能够发挥不同能源之间的互补效应，可以有效地规划各个能源子系统的能量耦合，在满足用能需求的同时提高能源的利用率[2]。通过对IES的能量深度挖掘，可以实现可再生能源就地消纳，这对于含有分布式可再生能源机组的IES优化调度具有重要作用，它不仅能够提高分布式可再生能源机组的传输效率，还能够降低传统化石能源机组高耗能带来的碳排放。因此，研究含储能的IES优化调度方法具有现实的工程意义。

目前，大量国内外学者正在研究IES的鲁棒优化调度问题，前沿的学术研究方向是如何平抑可再生能源机组出力的波动性，以提高IES的多能流整体利用率[3]。文献[4]阐述了在IES中装载电转气装置来降低弃能所带来的碳排放，并验证了风、光消纳的有效性。文献[5]阐述了在IES中加装碳捕集装置来捕获燃煤运行机组的高碳排放，以平衡系统的经济性和环保性。文献[6]建立了考虑光伏机组出力不确定性的鲁棒优化调度模型，同时采用随机优化的方法进行求解。文献[7]构建了含两阶段鲁棒优化调度的模型，可以降低IES与上级电网的能量交互。文献[8]考虑了风、光机组出力波动的严重不确定性，进而构建了含多元储能的IES鲁棒优化调度模型，其目的是提高分布式新能源的实时消纳率。文献[9]提出了多时间尺度的IES鲁棒优化调度策略，表明风、光机组在出力严重不确定性的情况下，灵活的日前-日内调度具有稳定的运行性能。

虽然风力机、光伏等分布式可再生能源机组可以为IES提供丰富的电能，但其出力的严重不确定性会影响到IES的稳定运行。针对分布式可再生能源机组出力不确定性的问题，大多数学者采用随机规划、鲁棒优化和模糊理论等方法[10]。这些传统数学规划方法存在着天然的缺陷，比如需要事先获取不确定参数的概率分布，或者需要根据参数概率区间设置可生成与可削减场景。为了解决这些问题，利用信息间隙决策理论去处理场景参数不确定性对机组优化调度的影响，在不依赖分布参数的情况下实现机组决策信息的优化，该理论算法在微网调度[11]、无功优化[12]和负荷预测[13]等领域得到科学应用，能够很好地抑制IES中风、光机组运行出力的时空间歇性和不确定性。

本文主要研究的是如何平抑可再生能源机组存在出力严重不确定性的问题，通过采取有效策略改善IES多能流利用率，以达到降低能源机组运行成本的目的。为了优化调度策略，需要以IES购能成本、设备运维成本和环境污染成本作为多目标适应度，并进一步处理风力机、光伏等新能源机组出力的严重不确定性，以构建出含风险规避的鲁棒优化调度模型。最后通过实验仿真，验证所提出的双层鲁棒优化调度模型可以在不同场景下对含储能的IES经济指标进行科学的分析。

1 IES结构及建模

广东粤北地区的冬季热负荷需求量较大，主要依赖于冷热电联供(combined cooling heating and power，CCHP)机组和燃气锅炉的热能供应，这将导致大量的机组碳排放。其中CCHP机组的联供运行方式会限制风、光电的上网交易空间，从而导致严重的弃风、弃光现象。通过在IES中设置多元储能装置，就可以有效打破传统CCHP机组“以热定电”的出力限制，使得其高碳排机组出力能够快速地响应不同负荷的需求[14]。本文构建了含多元储能的双层IES鲁棒优化调度模型，它可以有效提升能源系统中风、光电的就地消纳，减少弃风、弃光的能量阶梯浪费，其IES的结构如图1所示。该系统的电负荷由分布式新能源机组、CCHP机组、蓄电池以及上级电网联络线所组成；由燃气锅炉、CCHP机组和蓄热罐来提供用户侧所需要的热能；由CCHP机组、电制冷机和蓄冰槽来提供用户侧所需的冷能。

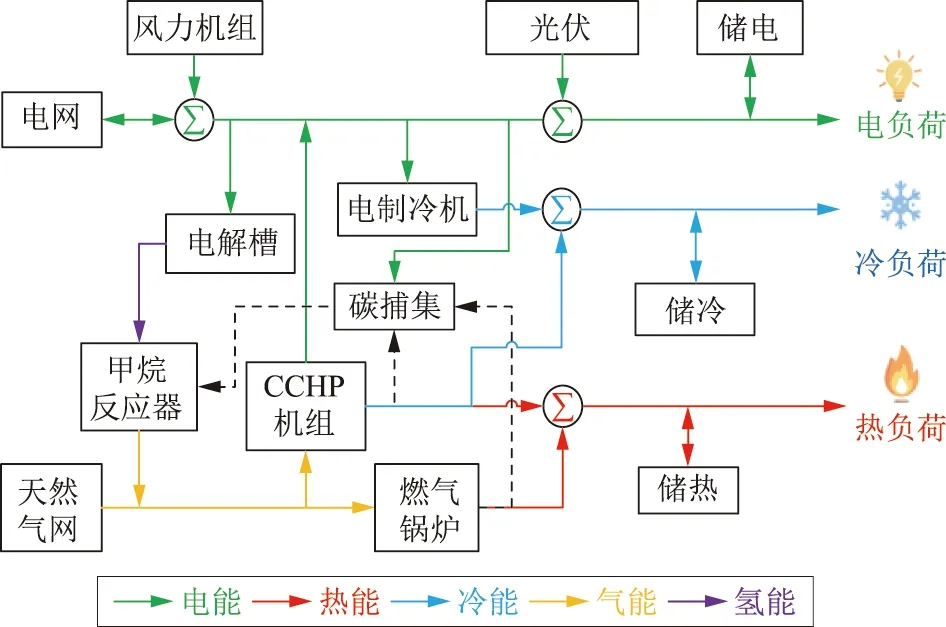
图1 IES结构模型Fig.1 IES structure model

1.1 CCHP机组模型

本文所建立的CCHP机组可以同时为用户提供多种类的供能负荷，主要内部装置包括微型燃气轮机、余热回收锅炉和吸收式制冷机[15]。微型燃气轮机用于供给IES电负荷，余热回收锅炉用于供给IES热负荷，吸收式制冷机用于供给IES冷负荷。其CCHP机组的模型如下：

a)微型燃气轮机。它作为CCHP机组中的主要供电耦合设备，可以有效地将机械能转变成电能进行用户侧持续供电，其输出电功率

PCCHP，e=ηeFMT，g.

(1)

式中：FMT，g为微型燃气轮机消耗的天然气；ηe为微型燃气轮机的电耦合效率。

b)余热回收锅炉。它通过回收燃气轮机发电过程中产生的余热，实现能量阶梯利用，以减少传递过程中的能量损失，其输出热功率

HCCHP，h=FMT，g(1-ηloss)ηh.

(2)

式中：ηh为余热回收锅炉的热转化效率；ηloss为余热回收锅炉的散热损失系数。

c)吸收式制冷机。它是利用化学反应来生成制冷功率的冷能耦合设备，能够在低温极端条件下持续地给用户侧供冷，其输出冷功率

CCCHP，c=ηcQMT，h.

(3)

式中：QMT，h为吸收式制冷机的吸收热功率；ηc为吸收式制冷机的冷耦合效率。

1.2 燃气锅炉模型

燃气锅炉通过燃烧天然气产生热能来有效补充CCHP机组产热不足时的热负荷，其输出热功率HGB与输入天然气功率GGB的关系为：

HGB=ηGBGGB.

(4)

式中ηGB为燃气锅炉的热能转换效率系数。

1.3 电制冷机模型

在CCHP机组无法满足供冷需求时，电制冷机会主动耗电制冷来补偿冷能量的不足，其输入电功率PAC与输出冷功率CAC之间的关系为：

CAC=ηACPAC.

(5)

式中ηAC为电制冷机的冷能转换效率系数。

1.4 电转气模型

电转气装置包含电解水和甲烷化这2个运行转换步骤，耦合的平均效率为45%～60%，其输出天然气功率GP2G与输入电功率PP2G的关系为：

GP2G=ηP2GPP2G.

(6)

式中ηP2G为电转气设备的转换效率系数。

1.5 碳捕集模型

碳捕集装置通过消耗大量电能来捕获CCHP机组和燃气锅炉释放出来的二氧化碳，机组能耗和捕获碳量有着密切关系，其输出捕获的碳含量TCCS与输入消耗电功率PCCS的关系为：

TCCS=ηCCSPCCS.

(7)

式中ηCCS为碳捕集装置的转换效率系数。

1.6 蓄电池模型

蓄电池是将化学能转化为电能，并稳定储存的电能量转换设备，为了避免在低荷电状态下充放电导致的使用寿命低问题，其运行工况需要满足荷电状态的容量约束。其模型表示为：

Ebt，t=Ebt，t-1+(ηbt，chrPES，c，t-PES，d，t/ηbt，dis)Δt.

(8)

式中：ηbt，chr、ηbt，dis分别为蓄电池的充电、放电效率转换耦合系数；PES，c，t、PES，d，t分别为t时刻蓄电池的储电、放电功率；Ebt，t为t时刻蓄电池的荷电功率当前储存量；Δt为单位时间间隔。

1.7 蓄热罐模型

蓄热罐是能量储热设备，它能够在荷侧热能富余时储存热能，并在热源不足时释放热能，这种储热设备具有削峰填谷的平抑功能，可以提高系统的耦合运行灵活性，其运行工况需要满足储热状态下的容量约束。其模型表示为：

Wbt，t=Wbt，t-1+(ηrt，chrHHS，c，t-HHS，d，t/ηrt，dis)Δt.

(9)

式中：ηrt，chr、ηrt，dis分别为蓄热罐的充热、放热效率转换耦合系数；HHS，c，t、HHS，d，t分别为t时刻蓄热罐的储热、放热功率；Wbt，t为t时刻蓄热罐的热能功率当前储存量。

1.8 蓄冰槽模型

蓄冰槽是用于蓄冰聚冷的储能设备，通过在冷能产量过剩时将水冰冻起来，并在冷能缺额时释放出来以满足用户冷能需求，其运行工况需要满足储冷状态下的容量约束。其模型表示为：

Bbt，t=Bbt，t-1+(ηlt，chrCCS，c，t-CCS，d，t/ηlt，dis)Δt.

(10)

式中：ηlt，chr、ηlt，dis分别为蓄冰槽的充冷、放冷效率耦合系数；CCS，c，t、CCS，d，t分别为t时刻蓄冰槽中的储冷、放冷功率；Bbt，t为t时刻蓄冰槽中的冷能功率当前储存量。

2 IES优化调度模型

2.1 目标函数

本文所建立的IES优化调度模型考虑了多层经济运行指标，包括上网购能成本、机组运维成本和环境污染成本。为了实现总成本最小化，需要将所构建的非线性混合整数规划模型约束条件与多层经济运行指标相结合，从而实现对IES目标适应度的数学建模[16]。其构建的目标函数如下：

minF=Fbuy+Fom+Fen.

(11)

式中：Fbuy为上网购能成本；Fom为设备运维成本；Fen为环境污染成本。

a)上网购能成本。含储能的IES购能成本主要由购电成本和购气成本组成。购电是通过与上级电网建立联络线，以大量购买荷侧缺额的电量来满足源荷之间的能量平衡；购气则是通过天然气管道，在天然气不足时购买IES所需的天然气来补充燃气供给。其购能成本

(12)

式中：Pt为t时刻的购电功率；λe为电力市场购电的分时电价；Gt为t时刻的天然气购买量；λg为天然气的分时价格；T为24 h 周期数。

b)设备运维成本。含储能的IES的能量耦合设备包括光伏机组、风电机组、CCHP机组、燃气锅炉、电制冷机、蓄电池、蓄热罐、蓄冰槽、碳捕集单元、电转气单元等。其运维成本

(13)

式中：Com，i为设备i的单位投资运维成本，下标表示为与设备i有关的变量；Pi，t为t时刻各耦合运行设备工作时的消耗功率。

c)环境污染成本。含储能的IES在机组调度过程中，CCHP机组和燃气锅炉所排放的二氧化碳是导致环境污染的主要原因，也是超额环境成本的主要来源，所以在IES调度燃煤机组时，必须考虑碳排放量对环境的影响。其环境成本

λCO2，CCHPGCCHP，t-λCO2，P2GPP2G，t.

(14)

式中：GGB，t为t时刻燃气锅炉供能时所需要输入的天然气功率；GCCHP，t为t时刻CCHP机组供能时所需要输入的天然气功率；PP2G，t为t时刻电转气合成天然气所消耗的电功率；λCO2，GB为燃气锅炉供热时产生碳排放的转换系数；λCO2，CCHP为CCHP机组供能时产生碳排放的转换系数；λCO2，P2G为电转气设备合成天然气所消耗二氧化碳的碳捕获系数。

2.2 约束条件

2.2.1 等式约束条件

含储能的IES优化调度模型主要包含等式约束和不等式约束条件，其中等式约束条件包括各种可调度机组在电、热、冷能量供需方面的多能平衡时空约束，而IES源荷供需量平衡又是确保系统可调度机组安全稳定运行的基础。

a)电功率平衡约束：

Pbuy，t+PWT，t+PPV，t+PCCHP，e，t+PES，d，t=

Pload，e，t+PES，c，t+PAC，t+PP2G，t+PCCS，t.

(15)

式中：PWT，t、PPV，t分别为t时刻风力机、光伏的预测电功率；Pload，e，t为t时刻的电负荷；Pbuy，t为t时刻的上网实际购电量；PCCHP，e，t为t时刻CCHP机组的燃气输出电功率。

b)热功率平衡约束：

HCCHP，h，t+HGB，t+HHS，d，t=HHS，c，t+Hload，h，t.

(16)

式中：HCCHP，e，t为t时刻CCHP机组的燃气输出热功率；HGB，t为t时刻燃气锅炉的输出热功率；Hload，h，t为t时刻的热负荷。

c)冷功率平衡约束：

CCCHP，c，t+CAC，t+CCS，d，t=CCS，c，t+Cload，c，t.

(17)

式中：CCCHP，e，t为t时刻CCHP机组的燃气输出冷功率；CAC，t为t时刻电制冷机的输出冷功率；Cload，c，t为t时刻的冷负荷。

2.2.2 不等式约束条件

含储能的IES优化调度模型的不等约束条件有多种表现形式，其中包括运行机组出力约束、爬坡约束和上网联络线交互约束等，在不同运行机组的约束前提下，调度结果会有明显差异，所以设置合理的不等式约束条件可以减少能量损失。

a)CCHP机组出力和爬坡约束：

(18)

式中：PCCHP，min、PCCHP，max分别为t时刻CCHP机组出力功率的最小值和最大值；PCCHP为t时刻CCHP机组出力功率；PCCHP，down、PCCHP，up分别为t时刻CCHP机组最小爬坡率和最大爬坡率。

b)燃气锅炉出力和爬坡约束：

(19)

式中：HGB，min、HGB，max分别为t时刻燃气锅炉出力功率的最小值和最大值；HGB为t时刻燃气锅炉的出力功率；HGB，down、HGB，up分别为t时刻燃气锅炉的最小爬坡率和最大爬坡率。

c)电制冷机出力和爬坡约束：

(20)

式中：CAC，min、CAC，max分别为t时刻电制冷机出力功率的最小值和最大值；CAC为t时刻电制冷机的出力功率；CAC，down、CAC，up分别为t时刻电制冷机的最小爬坡率和最大爬坡率。

d)电转气出力和爬坡约束：

(21)

式中：GP2G，min、GP2G，max分别为t时刻电转气出力功率的最小值和最大值；GP2G为t时刻电转气的出力功率；GP2G，down、GP2G，up分别为t时刻电转气的最小爬坡率和最大爬坡率。

e)碳捕集出力和爬坡约束：

(22)

式中：TCCS，min、TCCS，max分别为t时刻碳捕集出力功率的最小值和最大值；TCCS为t时刻碳捕集的出力功率；TCCS，down、TCCS，up分别为t时刻碳捕集的最小爬坡率和最大爬坡率。

3 IES双层鲁棒优化调度模型

本文采用信息决策间隙理论(information gap decision theory，IGDT)来处理IES中风、光机组出力波动的严重不确定性，以解决传统鲁棒优化调度过于保守和随机规划难以准确生成削减场景的运行调度问题[17]。过程包括3个步骤：建立带约束条件的向量集优化调度模型、建立新能源不确定集模型和建立风险规避型鲁棒调度模型。

3.1 向量集优化调度模型

现阶段IGDT在处理复杂的不确定性问题上已经表现出实用的工程效果，它通过比较预期结果和当前决策信息状况后修改约束条件范围，进而估算出系统的不稳定因素[18]。这种优化方法将原本含储能的IES鲁棒优化调度模型改写成带有条件约束的向量集优化调度模型，表达式如下：

(23)

式中：F(x，y)为优化模型的目标函数，x为系统决策变量，y为分布的不确定参数；H(x，y)为向量集优化模型的等式约束；G(x，y)为向量集优化模型的不等式约束。

3.2 新能源不确定集模型

在利用IGDT处理不确定性IES的新能源机组运行参数时，需要将不确定性概率区间分布转化为确定性预测变量集合，这个过程的转换是通过使用包络界区间来对不确定数值进行量化处理，并对新能源机组出力波动区间建模，表达式如下：

(24)

同时，当IES无法准确获取风、光机组不确定性参数的概率分布时，常用的随机规划方法难以准确描述其生成的可聚类场景，而IGDT可以处理这类参数信息不充分问题，进而使用包络边界区间来约束其功率能量波动的范围：

(25)

(26)

式中：aWT、aPV分别为风、光机组的出力波动不确定性幅度；PWT，pre，t、PPV，pre，t分别为风、光机组的预测运行电功率；PWT，t、PPV，t分别为风、光机组的实际运行电功率。

3.3 风险规避型鲁棒调度模型

传统的IGDT包含着风险规避方式的鲁棒优化调度模型，能够帮助保守型决策者应对严重的不确定性变化，从而降低IES的能量损失[19]。本文采用加权平方和的方式将2个不确定性参数和熵权法给定的调整权重结合起来，表达式如下：

(27)

式中：τWT、τPV分别为风电机组和光伏机组的不确定性出力波动的权重系数；ξWT、ξPV分别为风电机组和光伏机组的加权可调节系数；α为新能源机组出力波动的决策信息不确定度。

从风险规避的角度出发，为了能够降低模型评估风险出现的概率，需要确保IES的运行成本不会超过预期最恶劣的机组调度成本，这意味着需要承担更高风险的决策信息成本[20]。公式如下：

(28)

式中：maxφ为目标函数；F0为风、光机组不确定出力取预测值时的最优调度成本基准值；(1+μc)F0为预期调度目标的可接受成本范围；μc为风险规避偏差系数。

通过上述风险规避鲁棒优化调度模型，可以精确控制参数不确定性的变化范围。当新能源机组发电不足以满足日常供能需求的情况下，可以通过快速调度CCHP机组或燃气锅炉的出力来弥补联络线的功率缺额，进而转化为单层规划模型，即：

(29)

式中：aWT为风电机组的出力波动幅度；aPV为光伏机组的出力波动幅度；PWT，t为风电机组的实际功率值；PPV，t为光伏机组的实际功率值。

4 双层IES模型求解算法及流程

本文模型采用分段线性化的方法，将IES不确定性模型转化为确定性经济优化调度模型，并利用模拟退火粒子群优化(simulated annealing particle swarm optimization，PSO-SA)算法结合CPLEX求解器进行双层迭代求解。优化调度过程主要分为2个阶段：第1阶段是确定性的IES调度模型优化阶段，假设不确定参数的概率分布区间对应的预测值是准确的，就可以利用PSO-SA优化得出下层约束的基准值；第2阶段是不确定性的IES鲁棒调度模型优化阶段，通过处理IES中严重不确定性的机组出力波动，就可以采用风险规避型鲁棒优化调度方法计算出不确定性度，进而使用CPLEX求解器对下层目标适应度进行数值方法求解，获得最优的运行机组出力方案。

4.1 粒子群优化算法

粒子群优化算法(particle swarm optimization，PSO)属于种群更新的启发式优化算法，最初是受到鸟群觅食的灵感而创立的[21]。该智能优化算法具有简单且易实现的优点，能够在较短时间内搜索到近似的最优适应度，但由于在很大概率上无法找到全局的稳定最优解，实际工程中需要调整惯性权重或增加种群数量来提高算法性能。

4.2 模拟退火粒子群算法

PSO-SA属于混合型启发式优化算法，它结合着自然界鸟群捕食与物理退火过程的思想[22]。该算法的灵感来源于固体在温度降低时，其内部粒子群将由无序状态向有序状态转变。因此，在迭代计算过程中，粒子不仅可以接受优秀的个体解，还可以按某种特定概率接受被淘汰的较差解，这种突变机制提高了优化算法的收敛精度，从而保证混合型启发式算法的完备性。PSO-SA的步骤如下：

a)随机初始化种群中粒子的位置和速度。

b)计算每个粒子的适应度，将当前粒子的位置和速度存储在Pbest(即当前这一代粒子找到的最优适应度)中，同时将所有粒子中最优适应值个体的位置和速度存储在Gbest(即过去到现在所有粒子找到的最优适应度)中。

c)根据当前种群中粒子的位置和速度，更新其粒子状态，并生成下一代粒子群，其中后代的速度和位置更新计算公式如下：

vj(k+1)=wvj(k)+c1r1[Pbest-xj(k)]+
c2r2[Gbest-xj(k)].

(30)

xj(k+1)=xj(k)+vj(k+1).

(31)

式中：vj(k)为第k次迭代时第j个粒子的速度，k为当前迭代次数；xj(k)为第k代迭代时的第j个粒子的位置；w为惯性权重系数；c1、c2分别为个体和社会学习因子；r1、r2为0～1之间的随机数。

算法采用线性变化的自适应权重，让惯性权重w从最大值减小到最小值，且随迭代次数增加而逐步变化。权重w的自适应公式为：

w=wmax-k×(wmax-wmin)/kmax.

(32)

式中：wmax、wmin分别为初始惯性权重的最大值与最小值；kmax为最大迭代次数。

d)接着对产生的每一代粒子群均按交叉概率运算，同时利用模拟退火算法思想接受交叉后被淘汰的子代粒子群，并对其进行优化调整：

(33)

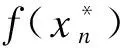
e)在对交叉操作后产生的新粒子群可以再按变异概率pm继续进行变异，接着利用模拟退火思想接受变异后的子代粒子群，接受变异后子代的公式与交叉概率运算的公式相同。

f)完成上述粒子群概率突变后，个体粒子开始进行模拟退火操作，粒子群降温公式为：

T(k+1)=c×T(k).

(34)

式中：T(k)为第k代粒子群的退火温度；c为系统冷却系数，取0～1之间的随机数，为了保证固态的粒子能够缓慢退火，通常取较大值。

g)在未达到预先初始设定的粒子最大迭代次数的情况下，转回步骤c)继续计算，而当达到设定的粒子最大迭代次数时，输出最终优化结果。

4.3 双层IES模型求解步骤

本文所建立的模型为双层规划模型。上层表示成本不超过预期时的最保守确定型场景，使用混合PSO-SA算法对目标进行优化，并将最优适应度作为约束信息传递到下层；下层表示实际可再生能源出力在不确定性区间内的变化，要求调度机组运行成本不得超过预期风险成本的最大值，再通过调用CPLEX求解器对模型进行求解，进一步实现目标函数的可控调度。通过上下层的迭代，可很准确地计算出不确定性IES模型中各运行机组的调度出力方案。算法求解流程[23]如图2所示。

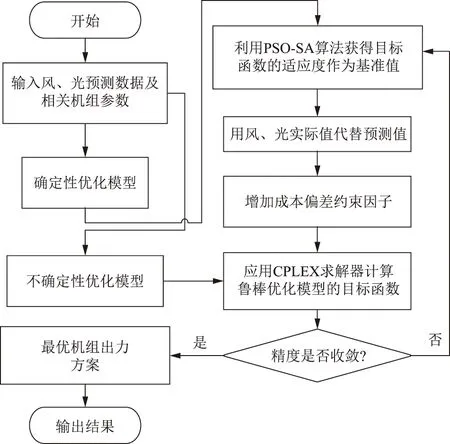
图2 双层IES优化调度模型求解流程Fig.2 Flow chart of solving two-level optimization scheduling model

步骤1：用风、光预测功率计算IES确定性经济调度模型，得到最优目标函数值，并将其目标适应度传递到下层作为基准值信息约束。

步骤2：用风、光实际值代替预测值，并制订风险成本可调偏差因子，从而确定决策者在可接受的优化模型期望下的目标值。

步骤3：迭代优化模型上下层，判断是否达到收敛精度或最大迭代次数。若不收敛，则调整成本偏差因子；若收敛，则输出调度结果。

5 算例分析

5.1 算例参数

为了验证本文所建模型的合理性，选择广东某园区级IES作为研究对象，并进行算例仿真。该工业园区以日前24 h为调度运行的周期，其多能负荷需求如图3所示；风、光机组出力功率预测结果如图4所示；表1为各设备的装机容量和转换效率；表2为上网购能的分时电价和气价。在仿真过程中，设置了1 h的时间步长间隔。上层模型使用PSO-SA算法求解确定性目标适应度，其混合启发式算法的种群数目设置为200组，最高迭代次数设置为500次，接着通过迭代优化的方式获得全局最佳适应度作为基准值信息传递到下层；下层模型在MATLAB_2021b软件内使用YALMIP工具包中的CPLEX求解器进行数值求解；最后通过双层迭代获得IES的日前调度最优出力方案。

表1 IES设备主要参数Tab.1 Main parameters of IES

表2 电、气分时价格Tab.2 Electricity/gas time-of-use electricity price

图3 多能负荷需求结果Fig.3 Multi-energy load demand results

图4 风、光功率预测结果Fig.4 Forecasting results of WTand PV

在IES的上层调度过程中，使用PSO-SA算法求解多目标适应度，从而得到各个运行机组的初步出力计划，接着将最优目标适应度作为基准决策信息传递到下层。上层仿真结果表明，优化后可以获得100个Pareto前沿解，这意味着有100种可选择的控制策略方案，但每个调度策略对应的适应度值各不相同，其优化结果如图5所示。

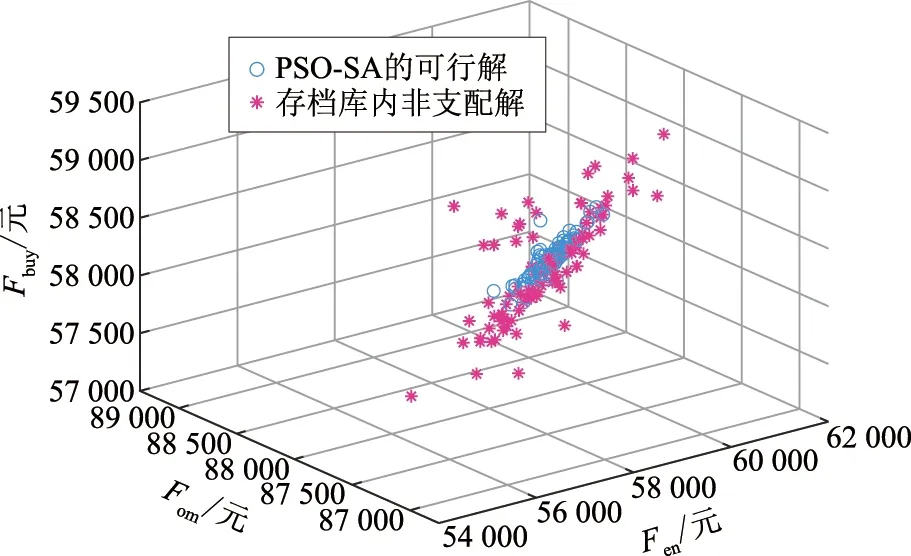
图5 基于PSO-SA算法的帕累托前沿解Fig.5 Pareto solution based on PSO-SA algorithm

5.2 场景调度结果分析

本节主要分析含不确定性的IES鲁棒优化调度模型，并设置2种场景进行对比。场景1：不含不确定性的多目标鲁棒优化场景，即日前经济运行调度场景；场景2：考虑新能源不确定性的鲁棒优化调度场景，即将IGDT方法应用于风、光不确定性出力处理后的可控调度场景。在IES鲁棒优化模型调度过程中，双层鲁棒优化调度将确定性模型的优化目标转化为求取风险成本不大于最大不确定性度的基准约束，得到的标定信息值越大，意味着保守决策方案对机组出力的不确定性程度变得相对更加不敏感，即IES的鲁棒性更好。

5.2.1 含不确定性的多目标优化结果分析

5.2.1.1 电功率平衡结果

在本文研究中，场景1被视为典型场景，在该场景下的电负荷主要由CCHP机组、风电机组、光伏以及电网交互联络线供给，而电制冷机、电转气装置和碳捕集装置则用于能量耦合，电功率平衡结果如图6所示。由于广东粤北地区在冬季有着大量的热负荷需求，而CCHP机组为了满足用户的生活热能需求，通常会在“以热定电”的模式下稳定运行供能，所以这种多能联供调度模式会导致大量的过剩电能量，进而出现就地弃能现象。

图6 电功率平衡结果Fig.6 Electric power balance results

5.2.1.2 热功率平衡结果

在场景1的基础上，IES的热负荷主要由燃气锅炉和CCHP机组共同出力满足，热功率平衡结果如图7所示。由图7可以发现：白天用户侧的热负荷需求不是很大，因此可以通过储热装置来储存过剩的热功率；而在夜晚机组运行时段，由于用户侧的荷需求量在逐渐升高，燃气锅炉会主动输出热功率来补偿IES热负荷需求的不足，同时蓄热罐释放储存的大功率热能量。通过燃气锅炉与蓄热罐的联合调度，可以使CCHP机组热出力达到IES荷侧热负荷的供需平衡，为风、光等分布式新能源机组出力腾出大量的能量耦合空间。

图7 热功率平衡结果Fig.7 Thermal power balance results

5.2.1.3 冷功率平衡结果

在场景1的基础上，IES的冷负荷主要由电制冷机和CCHP机组提供，用户侧的冷功率平衡结果如图8所示。由图8可以看出荷侧的冷负荷在需求量较低时是不需要CCHP机组工作的，而在高冷负荷需求下，只需要吸收少量的CCHP机组产热量制冷即可调节用户侧的冷能平衡；当用户侧的冷需求量较大时，会由电制冷机承担主要的动态冷负荷供给，同时释放蓄冷槽内储存的冷能量，进而满足IES荷侧的冷负荷能量供需平衡。

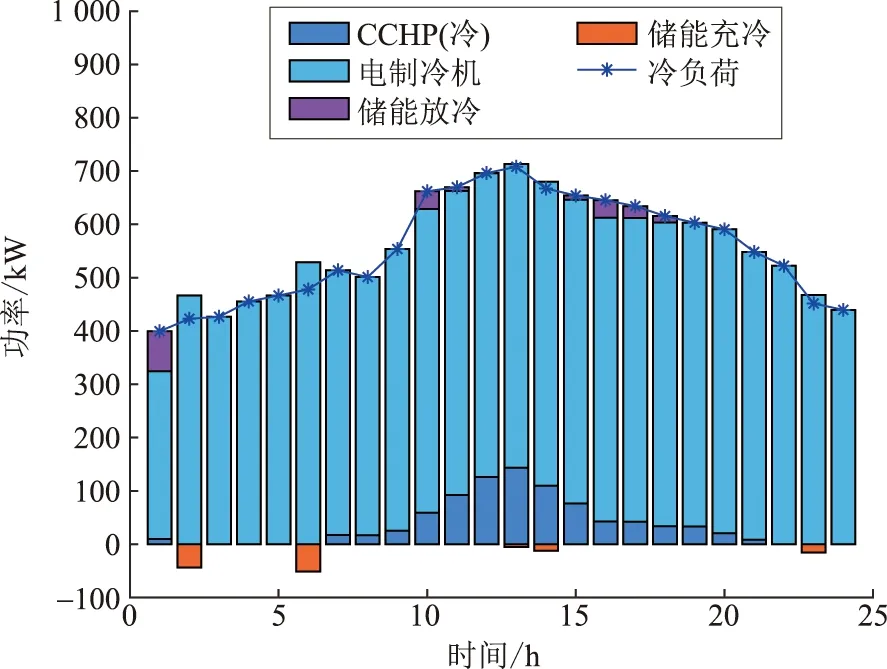
图8 冷功率平衡结果Fig.8 Cold power balance results

5.2.2 考虑不确定性的多目标优化结果分析

基于上述确定性场景的结果分析，进一步修正图6、7、8所示的风、光电预测出力值，并进行双层IES鲁棒优化调度。首先将风电的不确定度和光电的不确定度置0，此时的双层IES优化调度模型是不需要考虑不确定性的确定性模型，也即将风电预测值、光伏预测值以及各种网络机组参数带入模型后利用PSO-SA算法进行优化求解，得到的目标函数对应解就是鲁棒调度成本，这个解即称为基准决策信息；接着再利用这个基准值作为调度决策者制订双层IES优化运行策略的参考信息；随着风险规避系数的逐渐提高，下层目标的适应度在相同权重下会趋向更恶劣的调度场景，造成目标调度风险运行成本值同样升高，调度结果见表3。

表3 不确定性场景优化调度结果Tab.3 Uncertainty optimization scheduling results

由于在IES鲁棒调度模型中考虑了风、光机组电产能波动不确定性的结果，将其与仅考虑确定型目标优化调度结果相对比，可以发现在不同规避系数的调控下，其购能成本、运维成本和环境成本均有明显变化。这表明参数分布不确定性对机组的运维效益和环境保护都具有重要影响，且随着风险规避系数的提高，决策者所能接受风险的能力会逐渐增强。这个过程中的风、光电出力波动不确定性虽然也在不断增大，但在上层提供基准值信息的限制约束下，IES依然会减少弃风、弃光量。

5.2.2.1 优化后电功率平衡结果

场景2考虑了风、光电出力的不确定性，在该调度优化场景下，用户侧的电负荷主要由CCHP机组、风电机组、光伏机组和上级电网交互联络线供给，但风电机组和光伏机组出力功率已经由原来的不确定性变为相对无误差的电功率输出。这样做虽然能够减少因为时间尺度周期长带来的预测误差而造成的额外机组调度策略损失，但增加了能源响应机组快速调度所需要的风险决策成本。优化后的电功率平衡结果如图9所示。

图9 优化后电功率平衡结果Fig.9 Optimized electrical power balance results

5.2.2.2 优化后热功率平衡结果

在场景2的基础上，双层IES用户侧的热负荷需求主要是由电锅炉和CCHP机组的热出力来共同满足底层热能的缺额功率，优化后热功率平衡结果如图10所示。同样是在确定了风、光电的输出功率特性后，为保证源荷两端的热平衡，需要在IES用热需求量较高时，由电锅炉来承担主要的热能量供应，以此减少CCHP机组的运行约束，同时通过燃气锅炉配合蓄热罐充、放热出力来平衡荷侧热能的变化，间接减少了阶梯能量损失。

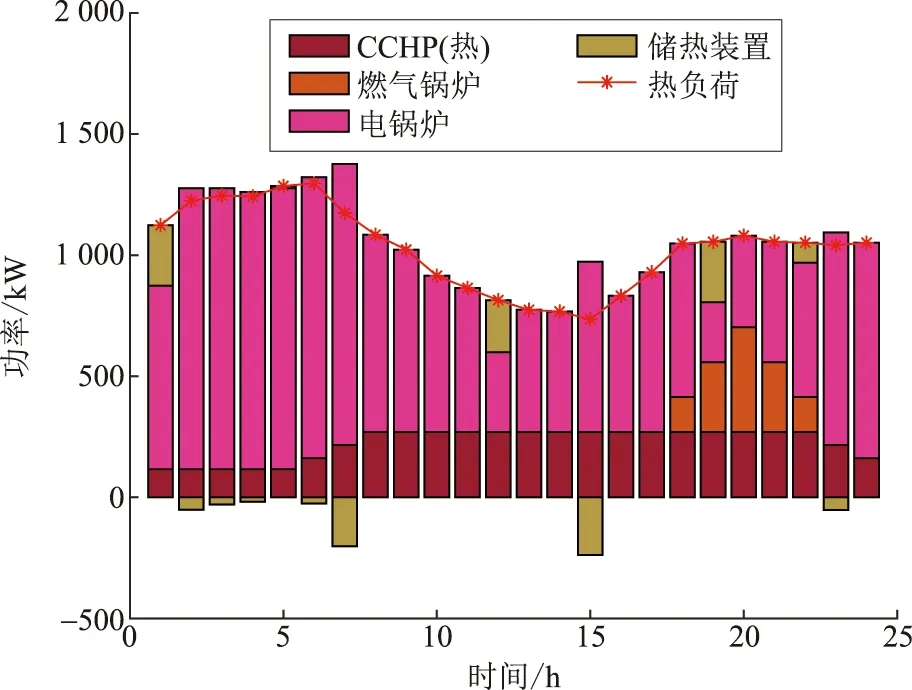
图10 优化后热功率平衡结果Fig.10 Optimized thermal power balance results

5.2.2.3 优化后冷功率平衡结果

在场景2的基础上，双层IES的冷负荷主要由电制冷机和CCHP机组的冷出力来共同满足底层冷能的缺额运行功率，优化后的源荷冷功率平衡结果如图11所示。在确定了风、光机组的运行输出特性后，冷负荷功率主要由CCHP机组承担底层的冷能需求量供应，而电制冷机和蓄冷槽起着冷负荷补偿运行耦合作用，减少了各机组调度过程中的能量损失，加强了不同能源间的深层耦合。

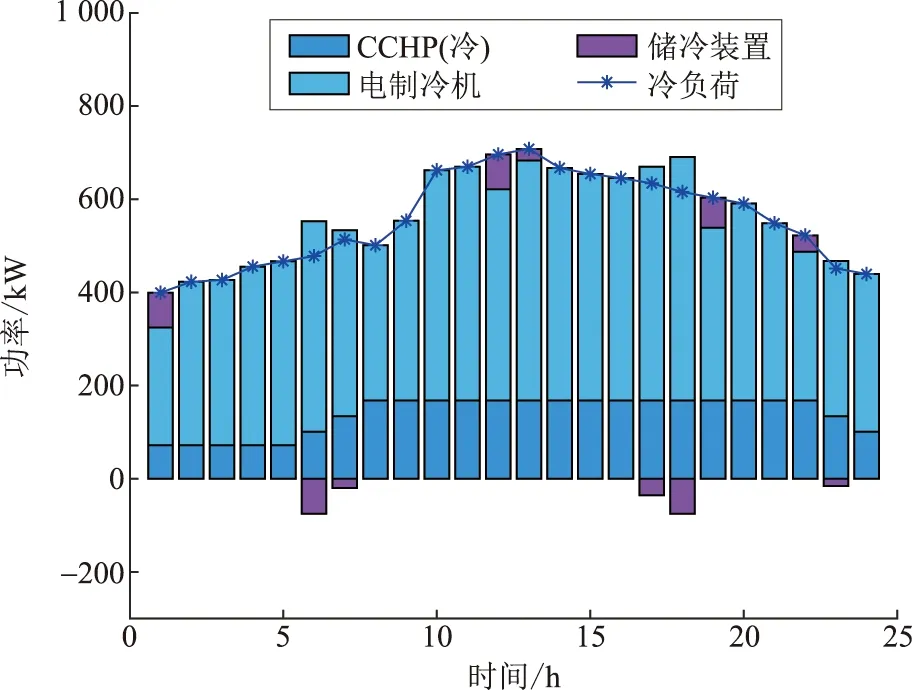
图11 优化后冷功率平衡结果Fig.11 Optimized cooling power balance results

5.2.3 模型有效性对比分析

为了验证本文所提双层IES鲁棒优化调度模型的优越性，将基于IGDT和PSO-SA的鲁棒优化调度模型分别与传统IGDT优化调度模型和确定性优化调度模型进行比较，同时对比了IES运行场景机组的调度成本、运行时间和迭代次数。上述3种模型在不同场景下的调度结果见表4。

表4 不同调度方法的场景对比Tab.4 Comparisons of different scheduling methods

由表4可知，采用本文所提出的双层鲁棒优化调度模型可以明显降低IES的运行成本，不仅可以减少风、光机组出力不确定性所造成的额外弃能经济损失，还能增强IES的鲁棒稳定性。在实际工程调度过程中，信息决策者应该对IES中严重不确定性的机组风险水平进行评估，再通过评估系统的决策信息来设置合理的风险规避系数，进而选择可接受风险范围内的最佳日前机组调度方案。

6 结论

本文为了平抑IES的能量瞬时高波动，详细分析了风、光机组出力的严重不确定性。首先通过构建确定性经济调度场景，同时考虑购能成本、机组运维成本和环境污染成本，并设置相应约束条件；然后在上层利用PSO-SA算法进行寻优，并将计算的适应度作为基准值传递到下层作为决策信息；接着在下层不确定性场景中接受来自上层的基准信息，并利用CPLEX求解器数值求解在信息约束下的鲁棒优化调度模型；最后通过算例仿真，验证了该双层鲁棒模型可以促进风、光电的消纳，减少IES的调度运行成本。主要研究成果如下：

a)本文建立了考虑新能源不确定性的IES鲁棒优化调度模型，相较于传统IES经济优化运行调度模型，该双层IES鲁棒优化调度模型在计算效率方面虽然会有所降低，但它在机组能量传递上由于增加了电转气和碳捕集的耦合，使得所建模型能够优化出更加精确的日前机组调度结果。

b)本文利用IGDT方法解决风、光机组出力波动的严重不确定性，与确定性鲁棒优化调度相比，该方法不需要考虑在最恶劣场景下和目标经济指标调度相冲突的矛盾，能够为调度工作者提供更加合理的机组调度决策信息。

c)本文利用PSO-SA算法求解确定性IES经济优化调度模型，并在上层多目标决策变量的约束条件下，增加了等式和不等式约束条件，接着对多目标函数进行求解，在获取帕累托前沿解后，选择最优适应度传递到下层作为基准决策信息。