高比例新能源接入的农村配电网网架多目标协同规划方法
2023-11-07刘志勇曾庆彬吴晗
刘志勇,曾庆彬,吴晗
(1. 南方电网广东韶关供电局,广东 韶关 512000;2. 广州市奔流电力科技有限公司,广东 广州 510700)
随着“双碳”目标的提出,清洁低碳的新能源发电技术得到快速发展,以光伏为代表的分布式新能源发电将大量接入配电网。对于电网网络基础薄弱的农村配电网,电网结构建设还不够完善,会出现供电线路的末端用户电压偏低、网络损耗过大等问题,并且难以消纳大规模的新能源接入[1-2]。现阶段,随着新能源的大规模规划建设,农村配电网将面临高比例新能源接入,为了帮助薄弱的农村配电网在经济安全运行情况下消纳高比例新能源,有必要研究高比例新能源接入的农村配电网网架协同规划方法,完善其电网网络,保证农村配电网用户安全可靠供电,最大限度消纳新能源。
目前,对于新能源接入的配电网网架规划问题,已有众多国内外学者从多方面展开研究:文献[3]建立基于安全性、可靠性和经济性评估的高中压配电网网架结构协调方案优选模型,并采用计及停电损失费用的总费用最小评估模型进行方案优选;文献[4]计及分布式电源输出功率的不确定性,以年平均投资运行费用模糊期望值最小为目标函数,提出含分布式电源的配电网网架规划方法;文献[5]考虑不同柔性负荷的运行控制策略,提出基于柔性负荷的配电网架规划模型;文献[6]考虑光伏电源和负荷随机波动性,提出基于电压偏差机会约束的、光伏电源极限接入农村配电网的容量计算方法;文献[7]为解决农村配电网电压质量低和网络损耗严重等问题,研究考虑低碳环保费用的、改善电压过低和网损过高的分布式光伏布点定容方案。文献[3-5]仅研究了配电网的网架规划,文献[6-7]仅研究了农村配电网新能源规划,对于配电网网架与新能源协同规划的现有研究仍然较少。文献[8]考虑稳态和故障运行下可靠性的综合评估体系,提出考虑可靠性的交直流混合配电网网架与分布式电源协同优化规划设计方法。上述研究的规划模型通常以经济性成本或者新能源消纳能力为目标函数,然而电网网络基础薄弱的农村配电网面临着电压偏低、网络损耗过大、消纳新能源能力较弱等问题,研究考虑多个维度目标的农村配电网网架和新能源的多目标协同规划模型具有重要意义。
不同于单目标优化问题,多目标优化问题存在多个非支配解。多目标优化问题通常先求解出所有非支配解构成的Pareto最优解集,然后决策者从Pareto最优解集中选取折中最优解作为优化决策方案,通常将与乌托邦解距离最小的解作为折中最优解。常见的多目标求解方法分为标量化算法和智能优化算法(也叫矢量化算法),其中标量化算法通常包括加权和法[9]、ε约束法[10]、法线边界交叉法[11]、规格化法平面约束法[12],智能优化算法通常包括非支配排序遗传算法[13]、多目标粒子群算法[14]、多目标微分进化算法[15]。然而,上述多目标求解算法都是求出Pareto最优解集,然后再从Pareto最优解集中选取折中最优解。当应用于3个及以上的多目标优化问题时,随着目标维数的增加,求解Pareto最优解集的计算时间快速增长,并且当系统规模较大时,计算负担会进一步加重;因此,亟需寻找更高效的求解多目标优化问题折中最优解的方法。
据此,面对高比例新能源接入的农村配电网,在研究中同时考虑3个维度的目标函数(即最小化投资运行费用、最小化电压偏差、最大化新能源消纳能力),并以农村配电网的规划建设网架线路以及新能源的选址和定容共同作为决策变量,建立农村配电网网架和新能源的多目标协同规划模型。针对多目标优化求解Pareto最优解集效率不高的问题,提出一种在多目标全体可行解中直接求解折中最优解的快速求解方法,获得农村配电网网架与新能源协同规划的多目标折中最优方案。
1 农村配电网网架和新能源的多目标协同规划模型
1.1 目标函数
针对上述高比例新能源接入电网网络基础薄弱的农村配电网时会出现问题,将研究农村配电网新能源站的选址定容规划,以及新增网架线路连接新能源站点与农村配电网的规划建设,协助农村配电网的新能源消纳,并改善农村配电网末端用户的电压质量。所建立的农村配电网网架和新能源的协同规划模型同时考虑了3个维度的目标函数,即最小化年等值投资运行费用minf1、最小化系统电压偏差minf2、最大化新能源消纳能力maxf3,见式(1)—(3)。其中,接入农村配电网的高比例新能源以分布式光伏为代表,年等值投资运行费用f1包括建设新增网架线路和光伏电站的年等值建设投资费用,以及农村配电网向上级电站购电的运行费用。
(1)
(2)
(3)
式(1)—(3)中:Cins为建设新增网架线路和光伏电站的年等值建设投资费用;ωline、ωpv分别为新增网架线路、光伏电站建设投资费用的年等值系数;δ为折现率;Tline、Tpv分别为新增网架线路、光伏电站的设备使用年限;μl和μpvi为0-1变量,μl取值1/0表示建设/不建设新增网架线路l,μpvi取值1/0表示节点i配置/不配置光伏电站;Ll为新增网架线路l的长度;Spvi为节点i配置光伏电站的容量;a0、b0分别为与新增网架线路、光伏电站建设安装个数有关的固定安装费用,包括土地开发、运输安装、支架杆塔等成本;a1、b1分别为与线路长度、光伏电站容量成正比的安装费用,包括建设材料、运行维护等成本;ΩG为上级电站的节点集合;Ωline、Ωpv分别为新增网架线路、光伏电站的候选线路或节点集合;Dy为一年包含的日数;cG为向上级电站购电成本单价;PGi,t为时段t节点i处上级电站的注入有功功率;T为运行周期的时段总数;Δt为时段间隔,取1 h;Ui、Ui,N分别为节点i电压的幅值、基准值;N为农村配电网的节点总数。
1.2 配电网运行约束
配电网运行约束包括配电网的支路潮流方程以及运行安全约束。采用二阶锥凸松弛的支路潮流方程描述配电网的运行状态约束[16],见式(4)—(7)。
Ppvi,t+PGi,t-PLi,t,
(4)
QGi,t-QLi,t,
(5)
(6)
(7)
式(4)—(7)中:σ(i)为首节点为i的支路所有末节点集合;π(i)为末节点为i的支路所有首节点集合;Rji、Xji分别为支路ji的电阻、电抗;Pik,t、Qik,t分别为时段t支路ik的有功功率、无功功率;Pji,t、Qji,t、Iji,t分别为时段t支路ji的有功功率、无功功率、电流;Ui,t、Uj,t分别为时段t节点i、j的电压;Ppvi,t为时段t节点i的光伏电站的有功功率注入量;QGi,t为时段t节点i的上级电站的无功功率注入量;PLi,t、QLi,t分别为时段t节点i有功负荷、无功负荷。
配电网的安全约束包括节点电压和支路功率的安全约束,上级电站向配电网注入功率的上、下限约束,以及变电站向配电网注入功率的连续调整约束,各约束式如下:
(8)
Pij,t,min≤Pij,t≤Pij,t,max,
(9)
PGi,t,min≤PGi,t≤PGi,t,max,
(10)
QGi,t,min≤QGi,t≤QGi,t,max,
(11)
-rdgiΔt≤PGi,t-PGi,t-1≤rugiΔt.
(12)
式(8)—(12)中:Ui,t,max、Ui,t,min分别为在时段t节点i的电压上、下限,用下标max、min分别表示各参数的上、下限,下同;rdgi、rugi分别为节点i处上级电站向配电网注入功率的单位时间向下、向上调整功率。
1.3 光伏电站运行和配置约束
研究中只考虑光伏电站的有功功率输出,其应该与相应节点的光伏配置容量成正比,故光伏电站的运行约束式为
Ppvi,t=SpviPrt.
(13)
式中Prt为单位配置容量的光伏出力。
光伏电站的配置约束包括每个节点的配置容量上、下限约束,并网节点的上限约束,实际工程中光伏配置容量Spvi应是单台光伏逆变器额定容量整数倍的约束,各约束式如下:
0≤Spvi≤μpviSpv,max,
(14)
(15)
Spvi=kpviSpv0.
(16)
式(14)—(16)中:Npv,max为农村配电网中规划接入光伏电站的数量上限;kpvi为节点i光伏逆变器配置数量;Spv0为单台光伏逆变器的额定容量。
1.4 新增网架线路运行和配置约束
针对规划建设的光伏电站,需要新增网架线路连接到农村配电网中,以帮助光伏电站并网消纳。新增网架线路的运行约束与常规线路的运行约束一致,如式(4)—(7)。新增网架线路的配置约束包括连接每个光伏电站的新增网架线路数量上限,以及配电网规划新增网架线路总量的上限约束,各约束式如下:
(17)
(18)
式中:Npv-line,max为连接每个光伏电站的新增网架线路数量上限;Nline,max为农村配电网中规划新增网架线路的总量上限。
综上,式(1)—(18)组成农村配电网网架和新能源的多目标协同规划模型,是混合整数二阶锥规划模型,包含了3个不同维度的目标。针对常用的多目标优化方法(加权和法、ε约束法等)计算效率较低的问题,研究中提出了一种快速求解多目标优化模型的折中最优解的方法,以高效获得农村配电网网架与新能源协同规划的多目标折中最优方案。
2 考虑光伏出力随机性的多目标优化模型的求解方法
2.1 考虑光伏出力随机性的场景法求解
针对光伏出力存在随机性,采用场景法通过对随机变量进行抽样生成大量的场景,从而将不确定优化模型转化为多个场景下的确定性优化模型。转化后的优化模型可表示为如下形式:
(19)
式中:ξ0、ξs分别为随机变量ξ的预测场景、第s个误差场景;x0、xs分别为预测场景、第s个误差场景下的决策变量;S为抽样的误差场景个数。场景法式(19)的目标函数为预测场景下的目标值。约束条件中,h0、g0分别为预测场景下的等式、不等式约束,hs、gs分别为误差场景s下的等式、不等式约束,g0s为预测场景与误差场景s之间的场景转移约束。此外,在场景法求解过程中,采用拉丁超立方抽样法对随机变量进行抽样,生成一系列的误差场景。
2.2 多目标优化模型的求解方法
对于多目标优化模型,具有p个优化目标的多目标优化模型可以写成
(20)
式中x、X分别为多目标优化模型的决策变量向量、全体可行域集合。
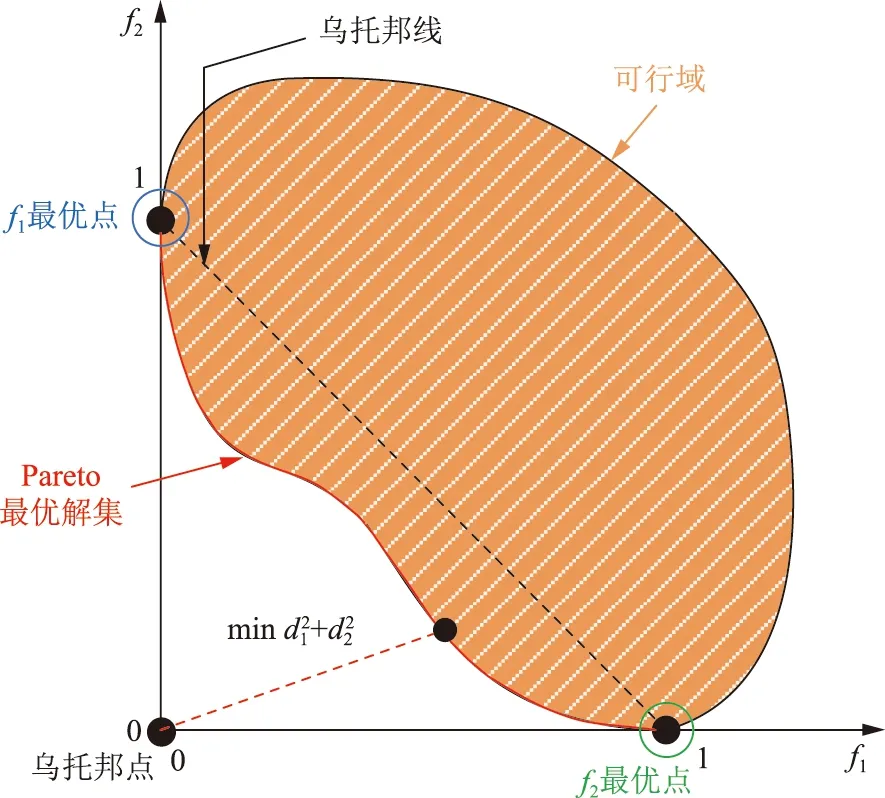
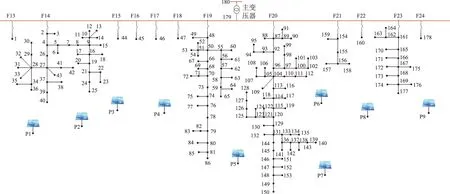
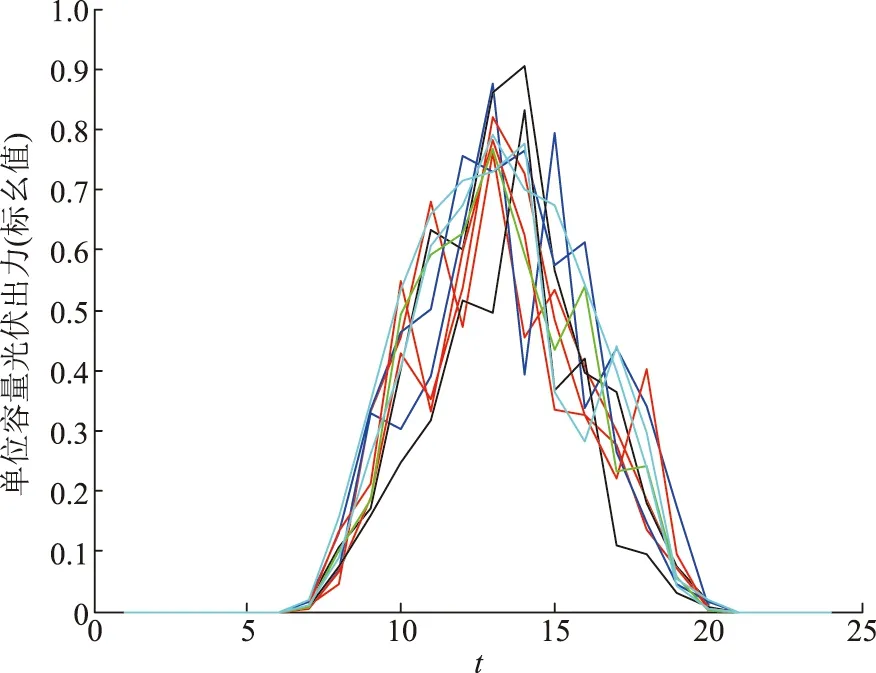
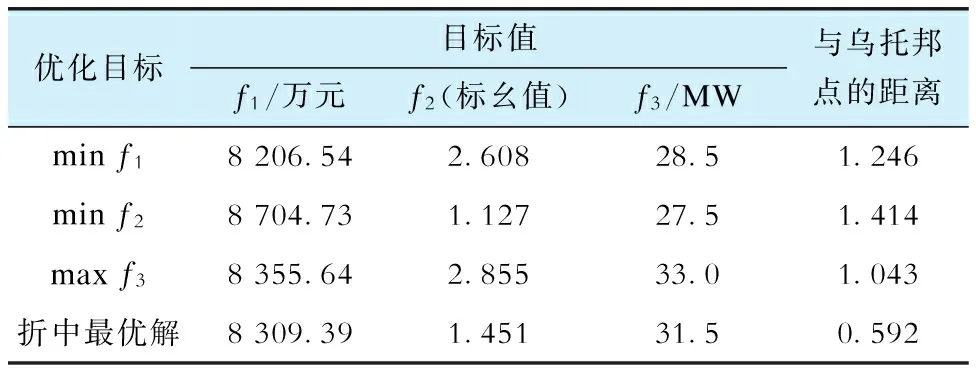
假设x1和x2均为可行解,且对任一目标函数都存在fa(x1) (21) (22) 采用加权和法、ε约束法等常用的多目标优化求解方法需要不断调整权重wa或者εa值,获得大量离散的Pareto最优解形成Pareto最优解集,再从该Pareto最优解集通常选取与乌托邦点距离最小的解作为多目标折中最优解。以两目标为例的原理图如图1所示。 图1 常用多目标优化方法求解两目标优化模型的原理Fig.1 Principles of solving two-objective optimization model by commonly used multi-objective methods 然而上述获得Pareto最优解集的求解过程需要求解出大量离散的Pareto最优解,会耗费大量计算时间,并且Pareto最优解集是由大量离散点近似构成,可能遗漏真正综合最优的折中最优解。为了提高计算效率以及获得更好的折中最优解,以最小化多目标优化解和乌托邦点之间的距离为目标,不需要求解出大量离散的Pareto最优解,在多目标优化模型的可行域中直接搜索与乌托邦点距离最小的解作为折中最优解(显然,这个折中最优解也在Pareto解集中)。并且所提的快速求解折中最优解方法在多目标优化模型的可行域中通过优化遍历所有的Pareto最优解,不会遗漏任何Pareto最优解,能获得真正综合最优的折中最优解。 本研究所提直接求解两目标优化模型的折中最优解的原理如图2所示,相比图1可以看出,所提方法不需要求解大量离散的Pareto最优解,直接通过优化遍历所有的Pareto最优解获得折中最优解即可。该方法的计算步骤为:①对每个目标fa(x)求解单目标优化模型,得到每个单目标最优解xa*和最优目标值fa(xa*),同时获得每个单目标最优解xa*对应的其他各个目标值f1(xa*),f2(xa*),…,fp(xa*)。据此,可以得到各个单目标最优值组成的乌托邦解(f1(x1*),f2(x2*),…,fp(xp*)),以及p×p支付矩阵Apay﹝见式(23)﹞。将支付矩阵中第a列的各元素的最大值记为fa,max。②以最小化多目标解和乌托邦解之间的归一化距离为目标,构建直接求解折中最优解的优化模型﹝见式(24)﹞。通过直接求解优化模型式(24)即可获得原多目标优化模型式(20)的折中最优解。 图2 直接求解两目标优化模型的折中最优解的原理Fig.2 Principle of directly solving compromised optimal solution of two-objective optimization model (23) (24) 式中:d为多目标解与乌托邦解之间的归一化距离;da为各单目标解与乌托邦解之间的归一化距离。 综上所述,考虑了光伏出力随机性和高比例新能源接入,本文所建立直接求解多目标折中最优解的农村配电网网架多目标协同规划模型如下: (25) 式中预测场景下和每个误差场景下的等式和不等式约束都包括式(4)—(18),预测场景与每个误差场景之间的场景转移约束为 -rdgiΔt≤PGi,t,s-PGi,t,s-1≤rugiΔt. (26) 表1 候选的新增网架线路连接到农村配电网节点的线路长度Tab.1 The length of line connecting candidate new grid line to rural distribution network node 图3 某个实际农村配电网系统拓扑图Fig.3 Topology of an actual rural distribution network system 图4 各个场景下的光伏出力特性曲线Fig.4 Photovoltaic output characteristic curves in each scenario 图5 配电网系统总负荷曲线Fig.5 Total load curve of distribution network system 分别计算以最小化年等值投资运行费用(minf1)、最小化系统电压偏差(minf2)、最大化新能源消纳能力(maxf3)为目标的单目标网架和新能源的协同规划模型,与在相应的单目标下的、不规划配置网架线路和新能源的原农村配电网最优潮流计算结果(以下简称“原最优潮流结果”)的对比见表2,其中最小化系统电压偏差与原最优潮流结果的节点电压在空间和时间2个方面的详细对比如图6、7所示。 表2 配电网网架和新能源的协同规划配置结果Tab.2 The collaborative planning and allocation results of distribution network and new energy 图6 配电网系统时段t=12下的各节点电压Fig.6 Voltage of each bus in time period t=12 of distribution network system 图7 配电网系统节点140的各时段电压Fig.7 Voltage of bus 140 in each time period of distribution network system 从表2和图6、7中可以看出,与原最优潮流结果相比,单目标优化下对农村配电网进行新增网架和光伏电站的协同规划,年等值投资运行费用可节省3 463.69万元,系统总电压偏差可降低72.5%,农村配电网新能源消纳能力可提高33 MW,可改善电网网络结构薄弱、供电线路的末端用户电压偏低、难以消纳大规模的新能源等问题。 采用所提出的直接求得多目标优化折中最优解的方法,得到支付矩阵式(23)并求解优化模型式(24),直接获得的多目标优化折中最优解的各个目标值和与乌托邦点的距离结果见表3,多目标优化折中最优解的配电网网架和新能源的协同规划配置结果见表4。 表3 多目标优化的各个目标值结果Tab.3 Results of each objective value of multi-objective optimization 表4 多目标优化折中最优解的配置结果Tab.4 Configuration results of multi-objective optimization compromised solution 从表3可以看出,与各个单目标优化模型求解得到的各个目标函数值相比,所求得的多目标折中最优解对应的各个目标函数值与乌托邦点的距离最小,综合优化程度最高,而且每个目标值都是仅劣于乌托邦点的对应目标值。从表2和表4可以看出,所求得的多目标折中最优解综合了各个单目标优化的结果,得到使得3个目标综合最优的方案,相比原最优潮流结果,实现了多个目标的同时改善(年等值投资运行费用节省3 360.84万元、系统总电压偏差降低64.6%、农村配电网新能源消纳能力提高31.5 MW),可以作为农村配电网网架和新能源的多目标协同规划配置的折中最优方案。 与其他常用多目标优化计算方法(加权和法、ε约束法)的对比结果见表5。ε约束法以第1个目标为主要目标,其余2个目标均视为ε约束转化为单目标优化模型,在归一化后的[0,1]范围内均匀取10个离散点,并计算每组ε值对应的单目标优化模型,得到每个Pareto最优解,然后选取距离乌托邦点最小的Pareto最优解作为折中最优解。在加权求和法中,将每个目标的权重系数在归一化后的[0,1]均匀划分为10个离散点,从而转化为单目标优化模型,并优化计算每组权重系数下对应的Pareto最优解,然后同样再选取出折中最优解。 表5 与常用多目标优化方法的对比Tab.5 Comparison with common multi-objective optimization methods 常用的加权和法、ε约束法只能先获取有限数量的Pareto最优解,然后再从Pareto最优解集中选择折中最优解;而所提出方法可以直接在整个可行域中搜索求得折中最优解,因而其获得的折中最优解与乌托邦点的距离更小(见表5),综合优化程度更高。在求解效率方面,与加权和法、ε约束法相比,所提出的方法无需求解出所有的Pareto最优解,在耗费的计算时间上减少了数十倍,大大提高了计算效率。 面对高比例新能源接入的农村配电网,研究中同时考虑了3个维度的目标函数,即最小化投资运行费用、最小化电压偏差、最大化新能源消纳能力,建立农村配电网网架和新能源的多目标协同规划模型,并以某个实际180节点农村配电网作为算例进行分析,得出了以下结论: a)所提出的农村配电网网架和新能源的多目标协同规划方法,可以提供多目标规划配置的折中最优方案,实现农村配电网年等值投资运行费用、系统总电压偏差、新能源消纳能力等多个目标的同时改善。 b)与其他常用多目标优化方法相比,所提出的在多目标全体可行解中直接求解折中最优解的快速求解方法,不仅能得到综合优化程度更高的折中最优解,而且也极大提升了计算效率。
3 算例分析
3.1 算例参数设置
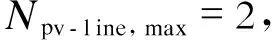


3.2 配电网网架和新能源的协同规划配置结果分析



3.3 多目标优化配置结果分析

3.4 与常用多目标优化方法的对比

4 结论
