基于一体式再生燃料电池的并网型微电网系统建模及分析

2023-11-07颜玉林张籍刘洋郭文瑞李平安迟赫天杨萌邱殿凯

广东电力 2023年9期

颜玉林，张籍，刘洋，郭文瑞，李平安，迟赫天，杨萌，邱殿凯

(1. 国网湖北省电力有限公司经济技术研究院，湖北武汉 430077；2. 上海交通大学机械与动力工程学院，上海 200240；3. 国网经济技术研究院有限公司，北京 102200)

氢气直接燃烧或通过燃料电池发电的产物为水，能够实现真正的零碳排放，是目前已知能源中最清洁的一种，被誉为21世纪的终极能源[1]。随着全球能源安全形势和气候问题日益严峻，世界各国持续增大对氢能行业的投资与科技研发力度，在碳中和背景下，基于可再生能源的“绿氢”相关技术成为行业聚焦的热点之一[2]。其中，一体式再生燃料电池(unitized regenerative fuel cell，URFC)作为一种既可以在燃料电池(fuel cell，FC)模式下消耗氢气发电，又可以在电解水(water electrolysis，WE)模式下消耗电能制取氢气的电化学装置，凭借其高比能量、清洁可再生的特性，在国内外氢能产业快速发展的大背景下，具有广阔的应用前景[3]。具体到电力系统方面，将URFC与风力机(wind turbine，WT)、光伏(photovoltaic，PV)等新能源发电机组相结合，通过URFC实现电能与氢能的双向灵活转化，可以有效增强电力系统的灵活调节性能，助力改善新能源发电的间歇性和波动性[4-6]。

随着分布式新能源的快速发展，近年来基于WT、PV等分布式能源打造的微电网系统已逐渐成为电力行业新的研究热点[7]。在微电网系统的投资建设以及运行维护过程中，选择合理的调节手段(如机械储能、电化学储能等)，并科学确定容量配置，对于保障微电网系统的安全稳定运行、提升系统投资收益具有重要的现实意义。以URFC作为微电网调节手段，其双向调节性能可以有效支撑削峰填谷，平滑电力波动。URFC系统的储能上限不受电池本身影响，而取决于外置储氢装置规模(如储氢罐容量等)，这极大地提升了其长时储能与调节能力。URFC具有较宽的工作区间，启停响应快[8]，可有效保障微电网系统实时安全稳定运行。总体来看，与锂离子电池等储能技术相比，URFC较好地兼顾了调节功率与能量的平衡，使其在跨季节、大规模储能的场景下具有相对较好的技术经济性。

从经济性方面来看，相较于传统大电网，微电网系统的投资具有更明显的商业属性，系统投资回报率是投资者重点考虑的关键因素之一。由于微电网系统的运行通常涉及到自发电、外购电、负荷、储能等多种系统变量，如何科学、合理地确定系统内各类单元的容量配比与运行模式，在保证微电网系统可靠运行的前提下，充分提升其整体经济效益，依然是目前亟需解决的问题。近年来，已有学者开展了以电-氢耦合为调节技术的多能源系统配置研究，证实了氢储能应用于分布式可再生能源发电系统的显著优势[9-11]。然而，现有研究多采用独立的电解槽和FC进行组合配置。相较于URFC，分离的装置不仅增加了系统设计与搭建的复杂程度，也不利于系统整体投资建设成本的优化降低。此外，对于系统最优容量配比设计，现有研究也提出了多种优化策略。文献[12]以最小配置容量为优化目标，采用上下限约束法及加权移动平均控制法，实现了混合能源装置接入微电网。文献[13]提出采用分时段优化策略来配置电池容量，充分利用风光互补特性，并实现了储能系统的并网运行。文献[14]利用离散傅里叶变换对微电网中产生的净负荷功率进行分解，建立两阶段混合能源容量优化的数学模型，并提出应由电网和混合能源装置共同平抑电网的波动负荷。文献[15]针对新能源发电出力的波动性，将滑动平均法和经验模态分解相结合，提出了一种混合储能平滑新能源出力优化配置方法。文献[16]综合考虑经济成本及碳排放，采用遗传算法对微电网电源配置建立优化模型，并通过改进算法提高了模型的准确性。然而，URFC作为兼顾电解制氢和氢气发电2种运行模式的电化学装置，对微电网系统容量配置的优化策略提出了新的要求，上述优化路线存在方法复杂、计算偏差大等局限性。

针对上述问题，本文提出一种基于URFC的并网型微电网系统，并以系统经济性指标最优为标准，指导开展系统容量优化配置。具体以湖北省某工业园区的微电网系统项目为研究对象，建立基于分布式WT、PV机组和URFC的并网型微电网系统成本描述模型，引入绿色排放因子，采用净现值(net present value，NPV)作为并网型微电网系统投资合理性的经济评价指标。针对不同季节的可再生能源资源(如光照、风速等)的分布差异，提出氢电供应因子用于协调并网型微电网系统的能源调度。最后通过粒子群优化(particle swarm optimization，PSO)算法优化微网系统各设备的容量，实现系统投资建设与运营运维成本最优，从而实现合理的投资回报率。

1 基于URFC的并网型微电网系统构成

区别于传统微电网系统，基于URFC的并网型微电网系统结构组成如图1所示，主要包含外部电网、新能源发电模块(WT和PV机组)、电-氢双向转换系统(URFC和储氢系统)以及用电负荷。

图1 基于URFC的并网型微电网系统结构Fig.1 Grid-connected microgrid system architecture based on URFC

整个微电网系统以WT和PV机组作为主要电力供给，URFC作为电能与氢能转换装置，助力协调微电网系统的实时电力供需平衡。在风能和太阳能充裕的时间段，URFC切换至WE工作模式，将新能源发电系统的过剩电量转换为氢能，并由储氢系统储存；在风能和太阳能匮乏的时间段，除依靠外部电网供电外，URFC可切换至FC工作模式，将储存的氢气转换为电能。采用上述运行模式，不仅可以实现园区电力可靠供应，还可最大程度地降低微电网系统的全生命周期碳排放，实现可观的环境效益。

该系统优先利用新能源系统自发电量和URFC发电满足用电需求，电网购电次之。因此，合理配置WT、PV和URFC等装置的容量，分析并制定最优的系统运行模式，是保证该并网型微电网系统高效、稳定、经济运行的关键。

1.1 URFC功率模型

在FC模式下，在URFC电池两极分别通入H2和O2发生氧化还原反应生成水，并对外输出电能；在WE模式下，通过外部的电能输入，发生析氢、析氧反应，在电池两极分别析出H2和O2并加以储存[17-18]。2种工作模式可自由切换，在WE模式下可将微电网系统中的冗余电能转换为氢能储存，FC模式下可将氢能转化为电能输出，氢能与电能之间的转换效率是决定电池运行成本的关键。

URFC在FC模式和WE模式下的性能均由不同电流加载情况下的极化行为决定。URFC在不同电流下的电压可表示为可逆电势活化过电位、欧姆过电位和浓差过电位之和(在FC模式下，过电位为负；在WE模式下，过电位为正)，即

Ucell=E+ΔVa++ΔVa-+ΔVc-+ΔVc++ΔVomic.

(1)

式中：Ucell为URFC输出电压；E为可逆电势；ΔVa-、ΔVa+分别为发生在负极、正极催化层的活化过电位；ΔVc-、ΔVc+分别为负极、正极的浓差过电位；ΔVomic为欧姆过电位。

工作效率是URFC的主要评价指标之一，

ηFC=Ucell/E，

(2)

ηWE=E/Ucell.

(3)

式(2)、(3)中：ηFC为FC模式的发电效率；ηWE为WE模式的电解效率。

URFC系统在FC模式下的输出功率

PU_FC=IηDCUcell，

(4)

在WE模式下的输入功率

PU_WE=IηDCUcell.

(5)

式(4)、(5)中：I为输出电流；ηDC为DC/DC转化效率。

1.2 WT机组数学模型

WT机组的实际输出功率与当地实时风速和机组额定输出功率有关，其数学表达式为[19]：

(6)

式中：PWT(v)为WT机组的实际输出功率；v0为WT起始工作风速；vp为WT额定工作风速；vc为WT截止工作风速；v为实际风速；PWT，o为WT额定输出功率；ηWT为WT机组的发电效率。

1.3 PV机组数学模型

PV机组采用单晶硅PV板串联的形式。PV机组的实际输出功率与当地的实时光照强度、环境温度及机组的额定功率相关[19]：

PPV(Gc，Tc)=

PPV，0ηPV(Gc/Go)[1+k(Tc-To)].

(7)

式中：PPV(Gc，Tc)为PV机组的实际输出功率；PPV，0为PV机组的额定功率；Go为标准条件下太阳辐照度；Gc为所在地区实时太阳辐照度；k为功率温度系数；To为标准条件下温度；Tc为所在地区实时温度；ηPV为PV机组的发电效率。

2 并网型微电网系统NPV优化方法

在经济学中，NPV是将项目全生命周期内所投入的净现金流量折现到项目建设初期的数目。NPV为正值表示该项目盈利，具有投资可实施性；NPV为负值则表示项目盈利水平较低，不适合投资。

2.1 并网型微电网系统NPV函数

对于基于分布式新能源及URFC的并网型微电网系统投资者，其成本主要包括各类设备的初始投资成本、设备运营和维护成本、外购电成本，其收益主要包括向微电网系统内用户的售电收益、向外部电网的售电收益以及环境效益。微电网投资者在保证系统内用户的稳定电力供应前提下，寻求最优的投资策略。值得注意的是，由于受到季节性影响，光照强度、风速等在不同季节的分布存在明显差异，如何配置不同季节条件下的微电网系统电力供给(自发电、外购电)组成，以实现系统经济效益最优，是优化微电网系统设计的关键。

综合考虑微电网系统的多种成本构成，其NPV可表示为：

(8)

Ry=[(a+1)y-1]/[a(1+a)y].

(9)

式(8)、(9)中：下标ydt表示第y年第d日第t时段的参数；y为生命周期年数；N为生命周期上限值；a为年利率；Ry为折算系数，主要作用是消除正常通货膨胀对资产评估的影响；Lydt为系统每小时用电量；Sydt为购电价格，当日不同时段(低谷、平段、高峰、尖峰)的价格不同；Gr，ydt为绿色排放因子；Dydt为每小时向外部电网售电量；S0为售电价格；My为发电机组第y年所需的维护和运营成本；C0为初始投资成本；λ为氢电供应因子。

2.1.1 运营和维护成本

运营及维护成本M包括WT、PV机组及URFC系统运维的人工成本Mu、物资成本Re。考虑整个生命周期中发电机组的部件使用寿命，M可表示为：

M=∑(Mui+Rei)Ci，i∈{WT，PV，URFC}.

(10)

式中Ci为i类分布式能源设备(用下标i表示，下同)的系统容量。

分布式能源单位容量所需年维修及运行费用见表1。

表1 分布式能源单位容量所需年维修及运行费用Tab.1 Annual maintenance and operating costs per unit capacity of distributed energy

2.1.2 初始投资成本

初始投资成本C0包括WT、PV发电机组及URFC系统设备的购置费用Ir、系统配套零件的购置费用Id和系统设备的安装费用Iu，即

C0=∑(Iri+Idi+Iui)Ci，i∈{WT，PV，URFC}.

(11)

分布式能源单位容量初始投资成本见表2。

表2 分布式能源单位容量初始投资成本Tab.2 Initial investment cost per unit capacity of distributed energy

2.1.3 绿色排放因子

传统火力发电厂在发电的同时会排放大量温室气体与有害气体，造成一系列气候和环境问题。在全球可持续发展与碳中和背景下，WT、PV等新能源发电系统的环境价值持续凸显。为体现新能源发电机组绿色排放的优势，本研究提出绿色排放因子，具体为将传统火力发电的尾气排放费用转换为对新能源发电机组的激励。绿色排放因子可表示为：

Gr，ydt=∑i(∑jGjSj)Ciδi，

i∈{WT，PV，微型燃气轮机，柴油发电机}，

j∈{NOx，CO2，CO，SO2}.

(12)

式中：Gj为分布式能源产生单位电量所造成的温室与有害气体j的排放量(见表3)；Sj为温室与有害气体j的处理费用(市场单价)(见表4)；δi为i类发电机组实际发电量修正值。

表3 分布式能源产生单位电量所造成的温室与有害气体排放量[20] Tab.3 Hazardous emissions per kWh of electricity generated from distributed energy

表4 温室与有害气体的处理成本[20] Tab.4 Costs consumed to treat hazardous gases

2.1.4 氢电供应因子

氢电供应因子λ为并网型微电网系统自发电量占负荷用电量的权重。主要针对不同季度风光资源供给情况来确定微电网自发电量与从外部电网购电量的占比，以实现微电网系统效益最优。

2.2 边界条件

a)微电网系统需保证持续稳定的电能供应，即

∑Wi+Wgrid≥L.

(13)

式中：Wi为i类发电机组每小时发电量；Wgrid为从电网外购电量；L为微电网系统每小时用电量。

由于储氢系统的局限性，URFC仍然存在供电上限，所以在建设微电网过程中要设定合理的阈值Lc以应对突发事故，可表示为

PU_FC+Wgrid≥Lc.

(14)

式中PU_FC为URFC在FC模式下的功率。

b)电网中，URFC是氢气主要消耗源及制造源。URFC在FC模式下消耗的氢气量应不大于在WE模式下电解产生的氢气量，微电网系统才能在不依靠外购氢气的基础上实现稳定运行，即

∑(WAηWEηFC-PU_FC)≥0.

(15)

式中WA为可再生能源机组产生的过剩电量。

c)URFC在WE模式下的功率PU_WE需满足新能源机组余电消纳需求，即

PU_WEηWE-(PWT+PPV-Lλ)≥0.

(16)

3 结果与分析

本研究以湖北某工业园区作为研究对象，采用该地区的风速、太阳辐照强度等作为微电网优化模型的输入参数，全年共计8 760组数据。该地区2021年全年电力负荷曲线如图2所示，根据当地分时电价政策计算购电成本与售电收入。上层模型主要根据分布式能源系统容量模型及运行边界条件建立，下层模型主要应用PSO算法在MATLAB中进行求解。

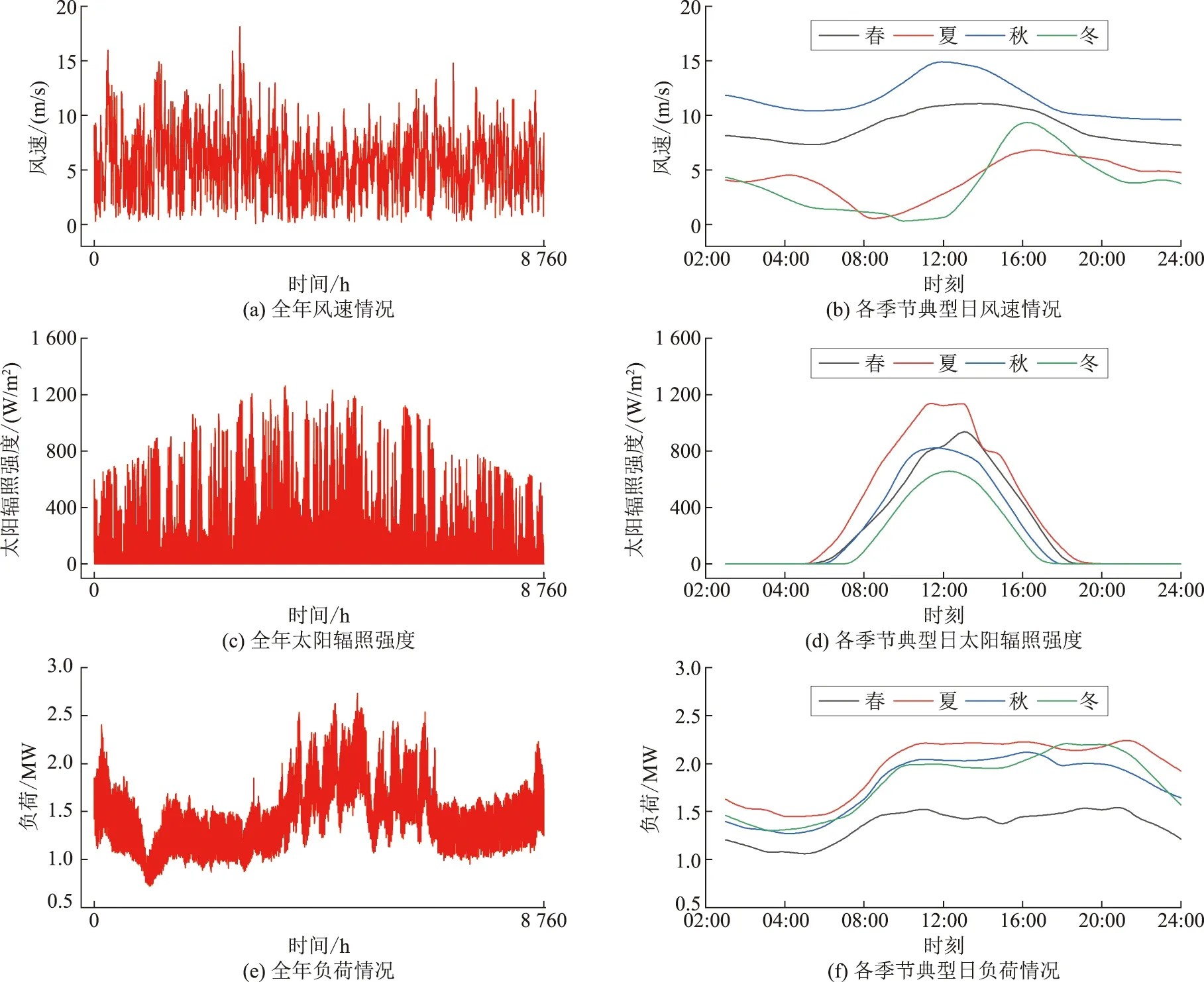
图2 湖北某工业园区风速、太阳辐照强度及负荷曲线Fig.2 Wind speed，radiation intensity and load data of an industrial park in Hubei

3.1 NPV计算结果

湖北省地处亚热带，为亚热带季风气候，光照充足，风力充沛。季风气候的4个季节存在明显的区别，这直接影响PV、WT的发电能力及微电网模型的优化。微电网系统容量与NPV优化结果如图3所示。

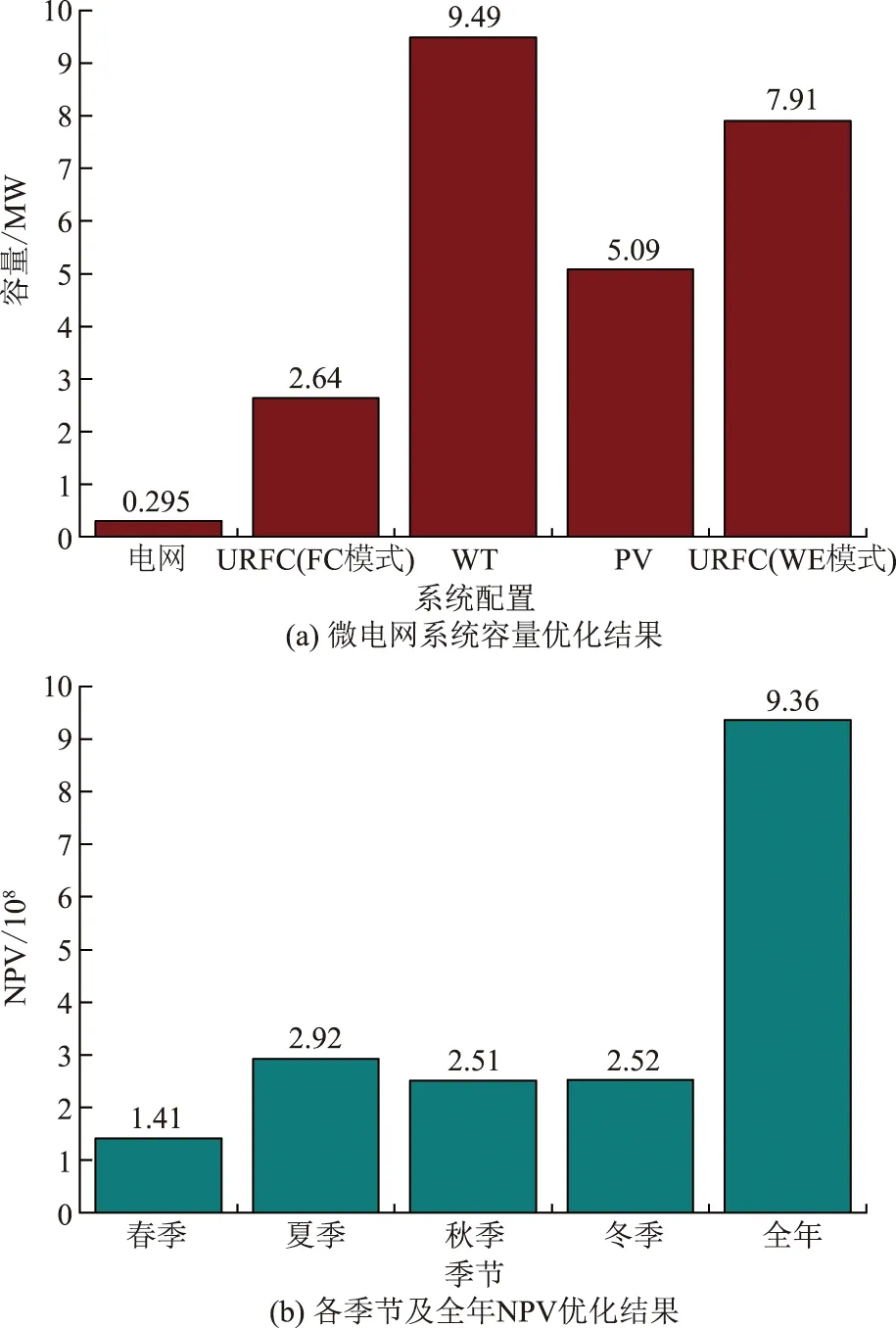
图3 微电网系统容量与NPV优化结果Fig.3 Capacity and NPV optimization results of the microgrid system

图3(a)为各个季度分布式能源系统容量优化结果，WT机组的装机容量比PV机组高4.4 MW，这是因为该工业园区在夜间仍具有一定规模的用电量需求，但是期间光照辐射强度为0，PV机组的出力特征不利于全天候的电力电量供需平衡。同时，该地区风力资源全天分布较为均匀，配置更多的WT机组可更好地解决因新能源资源分时供给不均而导致的电力供需矛盾。

图3(b)为全年及各季度NPV优化结果。整体来看，全年及各季度NPV均为正值，表明该项目具有投资可行性。具体来看，受该地区可再生能源资源与用电情况的季节性特征影响，春季NPV明显较低，夏季NPV相对最高。为进一步提升全年NPV总值，对季度NPV优化结果进行展开分析：春季的用电负荷明显低于其他季节，而售电所产生利润为微电网系统的主要利润来源，因此春季的利润更低；夏季同时拥有较多的可再生能源资源与用电负荷，因此夏季利润最高。值得注意的是，冬季的可再生能源资源匮乏，但用电负荷较高，在不改变其他条件的情况下，需要提高新能源发电系统装机容量才能满足微电网系统的正常运行。但是，增加发电系统容量，除了增加初始投资成本外，将导致新能源发电机组在其他3个季节产生更多的过剩电量，过剩电量可转换成氢能储存或出售给电网以增加微电网系统利润。因此，冬季是制约微电网系统配置的关键，调整冬季微电网系统自发电量占用电量的比例，或可为NPV提供进一步优化空间。

3.2 氢电供应因子敏感分析

为解决上述提出的矛盾，本研究引入氢电供应因子λ，代表冬季微电网系统自发电量占用电量的比例，其他季节不受影响，即λ=1时冬季负荷电量全部由微电网系统供应。考虑氢电供应因子λ后，微电网系统容量及NPV的优化结果如图4所示。

图4 考虑氢电供应因子λ后微电网系统容量及NPV的优化结果Fig.4 Optimization results of capacity and NPV of the microgrid system with consideration of λ

图4(b)为λ对不同季节以及全年NPV的影响。当λ<0.8时，全年NPV随λ增大呈上升的趋势，这是因为微电网售电利润随λ增加而增加。在成本方面，如图4(a)所示，主要通过调整外购电量来实现微电网电力电量供需平衡，WT、PV机组及URFC装机容量基本保持稳定，初始投资成本基本不变。当λ=0.8时，全年NPV达到最大值。当λ>0.8时，全年NPV随λ增大呈下降趋势，这是因为微电网系统的WT、PV机组及URFC装机容量逐渐增加，导致初始投资成本升高，额外的过剩电量带来的利润增长低于初始投资成本的增长。因此，当λ=0.8，即冬季外购电量占负荷电量的20%时，微电网系统的全年NPV将达到最大值。

3.3 系统输出功率变化趋势

对微电网系统某一日内分布式新能源能源发电机组输出功率进行分析，如图5所示：凌晨时段，由于光照辐射匮乏，系统主要由URFC(FC模式)和WT机组供电；日间时段，随着光照辐射强度及风速增加，WT机组和PV机组成为供电主力，并产生过剩电量，过剩电量由URFC(WE模式)转换为氢能；夜间时段，随着光照辐射强度降低至0，URFC(FC模式)及和WT机组再次成为系统供电主力。可见，此微电网系统可通过URFC在不同工作模式之间的灵活切换，适应不同时段新能源机组发电出力特征，实现微电网系统的稳定经济运行。