挖掘“轴对称”本质，建构知识体系

文／江苏省太仓市第一中学 陈明子

在学习“轴对称图形”的过程中，有一道题目的解法引起了我的兴趣。

原题呈现如图1，在四边形ABCD中，AC平分∠BAD，∠ABC+∠ADC=180°。求证：BC=DC。

图1

图2

这个题目是在学习了“角平分线的性质”之后的练习中出现的，我想到利用“角平分线上任意一点到角两边的距离相等”这一性质添加辅助线，作CE⊥AB，CF⊥AD，得到CE=CF，进而可证△CEB≌△CFD，所以BC=DC。

但是，在老师评讲这道题目的时候，我发现很多同学都和我的方法相同。因此，老师进一步启发我们，让我们再次观察角的特征。我忽然想起来角也是轴对称图形，角的两条边关于角平分线对称。我们过于关注“角平分线上任意一点到角两边的距离相等”，反而忽视了角的一般性，从这个角度想，我的思路就开阔多了。

证法二：如图3，在AB上取AG=AD，可证△ADC≌△AGC，得到CD=CG，再由角的关系得到CG=CB，所以BC=DC。

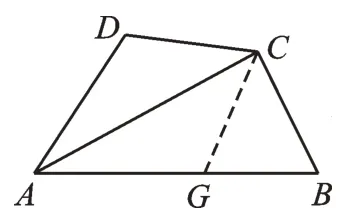
图3

有了上述题目的启发，我在看几何图形时，就不会局限于定理的应用，而是会看到图形的本质。我们不妨一起来试一试。

变式在△ABC中，∠C=2∠B。

（1）如图4，若AD平分∠BAC，求证：AB=AC+DC。

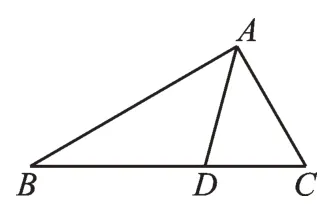
图4

（2）如图5，若AD是底边上的高，求证：BC=AC+2DC。

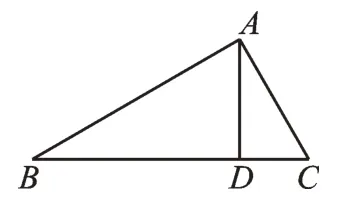
图5

（3）如图6，若BC=2AC，求证：∠BAC=90°。

图6

第（1）问中出现角平分线，如图7，我们可以利用轴对称性在AB上截取AE=AC，并连接DE（即作点C关于AD的对称点）或延长AC到点F，使得AF=AB，并连接DF（即作点B关于AD的对称点）。

图7

第（2）问中出现了底边上的高，如图8，我们可以利用垂直平分线的性质，在BC上截取DE=CD，并连接AE（即作点C关于AD的对称点）或延长BC到点F，使得DF=BD，并连接AF（即作点B关于AD的对称点）。

图8

第（3）问中出现了BC=2AC，要证明∠BAC=90°，即要证明∠B=30°，因此要采取的方法是利用等腰三角形的轴对称性进行等角的转换。如图9，作射线AD交BC于点D，使得∠BAD=∠B。

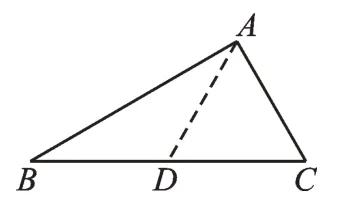
图9

通过对一道题的深入研究，我们才能透过现象看本质，从而解锁这一类题。在以后的学习中，我还会发现更多的轴对称图形，想到这儿，我越发兴奋，我要把我的“轴对称”体系不断地扩大！

教师点评：

轴对称变换是非常重要的一种几何变换，正如文中所提到的，很多同学往往只关注定理的应用，而忽略了“轴对称”的本质。小作者借助一个题目，抓住“轴对称”的本质进行深入研究，触类旁通，收获一类题，并体会到学习数学的乐趣，感悟数学之美！