基于BO-LSTM的天然气处理厂负荷率预测模型

刘 行 王秋晨 文韵豪 王 艺 巴玺立

1. 中国石油大学(北京)油气管道输送安全国家工程实验室·石油工程教育部重点实验室·城市油气输配技术北京市重点实验室, 北京 102200;2. 中国石油天然气股份有限公司规划总院, 北京 100080

0 前言

天然气处理厂是气田开发的重要地面生产设施[1-2],天然气处理厂连续、平稳、安全的运行直接关系到天然气的安全稳定供应[3],以及用户的生产和生活需要。天然气处理厂负荷率是一个关键性指标,它是指天然气处理厂的实际产能与设计产能之比。天然气处理厂负荷率的高低受原料气的质量、流量、设备运行状况、气体处理工艺流程、生产计划和管理等因素影响,直接关系天然气处理厂的生产效率和经济性。因此,有必要对天然气处理厂负荷率进行准确预测,以指导生产计划。

目前,较多学者使用时间序列预测模型对能源相关的数据进行了预测。梁倩雯[4]选用自回归积分滑动平均(Autoregressive Integrated Moving Average,ARIMA)、Prophet和长短期记忆(Long Short-Term Memory,LSTM)三种模型对管输下游不同用户群体的天然气平均负荷进行了预测,认为LSTM模型表现最好。Zheng Jianqin等人[5]采用粒子群算法对LSTM模型进行优化,与LSTM、ANN(Artificial Neural Network)、XGBoost(eXtreme Gradient Boosting)模型进行误差对比,突出优化模型的准确性,高效预测了太阳能发电量。Ning Yanrui等人[6]使用ARIMA、LSTM、Prophet三种模型和传统油品产量预测模型进行了产油量预测,预测误差显示ARIMA模型对于短期预测较为突出,Prophet模型整体的预测效果最好。田文才等人[7]提出一种小波变换分解的麻雀搜索算法(Sparrow Search Algorithm,SSA)-LSTM优化模型,用于预测华北某市燃气门站的天然气负荷,提高了预测精度。Fan Dongyan等人[8]集成了线性和非线性时间序列预测模型的优势,提出了一种ARIMA-LSTM-DP(Daily Production)的混合模型,对于油井产量预测表现较好。目前的研究大多基于传统预测模型进行开展,对于时间序列预测模型的改进和优化还可以继续进行。

现有研究较少对天然气处理厂负荷率进行预测,尚未形成通用的负荷率预测模型。天然气处理厂负荷率按照数据类型可分为平稳型和波动型。选取波动型负荷率和平稳型负荷率数据进行研究,提出基于贝叶斯优化(Bayesian Optimization,BO)-LSTM模型实现对天然气处理厂负荷率预测,极大地提高模型的计算效率和预测精度。同时,对比传统机器学习模型检验优化模型的优越性,天然气处理厂负荷率预测模型可为制定合理生产计划提供数据支撑,满足市场需求和避免天然气资源浪费。

1 计算方法

1.1 LSTM模型

LSTM是一种特殊结构的循环神经网络(Recurrent Neural Network,RNN),主要为解决传统RNN可能遇到的梯度消失和爆炸问题[9-10]。由于具有反馈连接,可以处理长期的数据序列,避免了一般RNN的长期依赖问题。LSTM内部由3个门实现控制传输,分别是遗忘门、输入门和输出门,结构见图1。图1中:g为隐藏层的输入状态;c为状态单元;h为隐藏层的输出状态;W为对应门的权重。

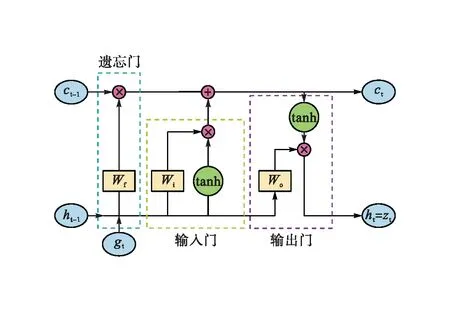
图1 LSTM原理结构示意图

遗忘门决定信息是否通过神经元传递,输入门决定新信息是否存储在神经元中,输出门决定信息是否作为当前状态的输出。模块中每个门由乘法运算和Sigmoid函数组成,Sigmoid函数控制通过门的信息,数值范围为0～1。Sigmoid函数的输出值和“tanh”层的候选值相乘作为神经元状态值。

1.2 贝叶斯优化算法

贝叶斯优化算法是一种全局优化方法,可以利用较少的迭代步数和已知数据去获取最优解,可用于调节机器学习算法的超参数。贝叶斯优化算法的核心由两部分构成:一是通过高斯过程回归建立目标函数的数学模型,即计算每点处函数值的均值和方差[11];二是根据后验概率分布构造采集函数[12-13],用于决定本次迭代时的最优采样点。

由贝叶斯定理可知[14-15]:

后验分布=先验分布+观察数据

(1)

(2)

f(x)=GP(m(x),C(x,x′))

(3)

采集函数根据后验分布构造,用于选择下一个采样点,即

(4)

贝叶斯优化超参数流程:

3)经过一定的迭代次数后,即可获得全局最优值。

1.3 BO-LSTM模型

在进行基本LSTM模型训练时,以典型天然气处理厂负荷率的历史数据作为输入,将当前时刻的天然气处理厂负荷率作为预测目标。网络层中超参数的设置对模型的预测性能有很大影响,由于超参数大部分通过手动调整,需反复试验才能获取较好的模型。因此,本文提出一种基于贝叶斯优化的超参数优化方法,实现自动选择超参数,提高模型的泛化能力,贝叶斯优化流程见图2。本研究主要是对LSTM网络的结构、隐藏层层数、隐藏层神经元个数、初始学习率和正则化系数进行贝叶斯优化,超参数范围设置见表1。

表1 LSTM网络超参数选择表

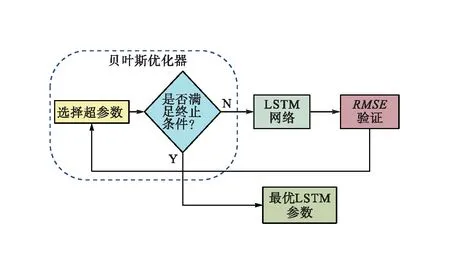
图2 贝叶斯优化流程图

BO-LSTM模型预测天然气处理厂负荷率流程见图3,基本步骤如下。

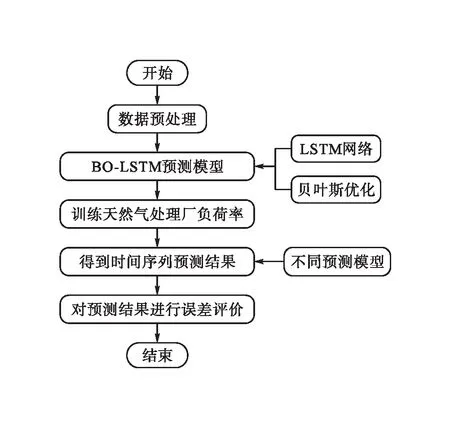
图3 BO-LSTM模型预测天然气处理厂负荷率流程图

2)数据归一化处理,并构建模型数据的训练集和测试集。

3)贝叶斯优化算法调节LSTM网络超参数。

4)利用优化后的BO-LSTM模型进行天然气处理厂负荷率预测。

5)在测试集上对预测结果进行误差评估,检验模型的准确度。

6)结束。

1.4 数据预处理

数据预处理部分包括数据收集、数据清洗、数据集划分、数据归一化等过程。本研究的天然气处理负荷率数据来源于某油气田处理厂的各季度报表,数据分训练集和测试集两部分。为了加快算法的收敛速度提高预测精度,需要对历史数据进行归一化处理。采用最大—最小标准化方法处理,将数据值映射到[0,1]。归一化表达式如下:

(5)

1.5 模型评价指标

(6)

(7)

(8)

2 实例分析

2.1 处理厂运行数据

本研究选取国内某油气田天然气处理厂(包含处理厂A、B、C、D)历史负荷率数据,样本数据记录了2017年6月1日至2022年2月28日的数据。剔除无效数据后,处理厂A、B、C、D的实际数据分别为1 734 d、1 711 d、1 711 d、1 670 d,原始数据见图4。数据集按照起伏情况分为波动型(处理厂A、B)和平稳型(处理厂C、D)。另外,按天然气处理厂负荷率高低划分为中低型(处理厂A、C)和中高型(处理厂B、D)。所选天然气处理厂数据覆盖面广,可用于检验模型的适应性。

图4 天然气处理厂负荷率原始数据图

由图4可知,仅处理厂B出现极少天数满负荷运行,天然气处理厂负荷率受天然气日处理量和检修天数直接影响,具有一定的时间序列特征。处理厂A、B受检修天数影响较大,天然气处理厂负荷率呈现明显的周期性波动;处理厂C、D的天然气日处理量变化较小,天然气处理厂负荷率总体呈平稳趋势。

2.2 模型对比

为了验证BO-LSTM模型的优劣,本研究选用反向传播神经网络(Back-propagation Neural Network,BPNN)、支持向量机(Support Vector Machine,SVM)、ARIMA、LSTM这4种传统时间序列预测模型作对比。BPNN模型是基于误差逆向传播算法的多层前馈神经网络,初始权值或阈值容易导致训练结果陷入局部最优值[17-18]。SVM模型可用于回归预测、分类预测,核心思想是在预测值与实际值的误差平方和最小的情况下找到一个最大间隔平面[19]。ARIMA(p,d,q)模型是常用的随机时序模型,将非平稳序列转为平稳序列,然后仅对目标参数的滞后值与随机误差项的现值和滞后值进行回归[20-21]。双向的(Bi-directional,Bi)LSTM模型是将LSTM网络分为向前和向后两个方向,综合考虑序列的历史和未来的数据,从而提高准确度。ARIMA模型的关键参数:p为自回归阶数,q为滑动平均指数,d为时间序列化为平稳时所需的差分次数。BPNN模型的神经元数目为50,学习率设置为0.5。SVM模型的惩罚系数取5.0,核函数选择常用的径向基函数(Radial Basis Function,RBF),RBF的gamma值取1.0。ARIMA模型的超参数由数据平稳性、赤池信息准则和贝叶斯信息准则确定[6,22]。LSTM模型隐含层层数为1,神经元数目为50,初始学习率为0.5,L2正则化系数为1×10-4。

2.3 模型验证

对比模型统一设置条件:时间序列模型的延时步长设置为30,最大迭代步数均为200。为防止模型过拟合,采用数据集的后10%数据作为测试集。初始的1组延时步长数据不做预测,故处理厂A、B、C、D的测试集样本数分别为144、142、143、137。通过贝叶斯优化算法寻找LSTM模型的超参数,经过多次迭代寻优,确定最优超参数值,BO-LSTM模型超参数的最优值见表2。

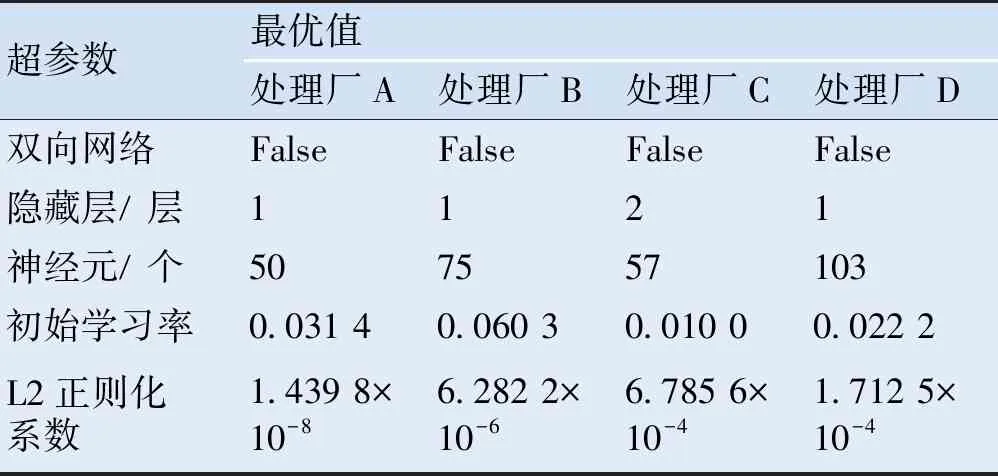
表2 BO-LSTM网络超参数表

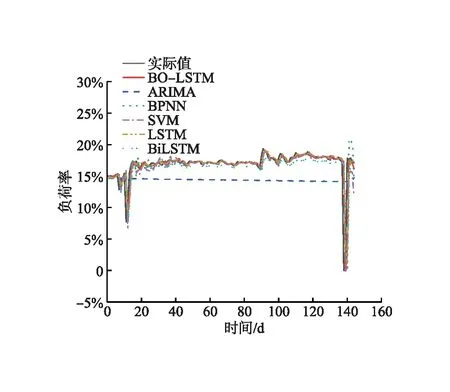
a)预测结果

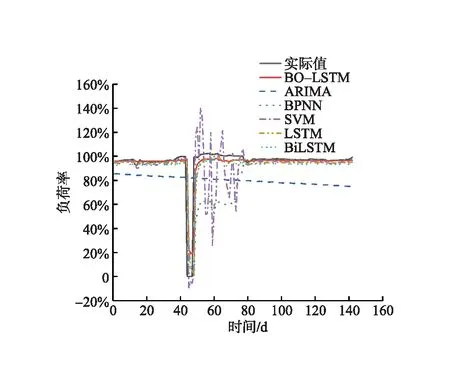
a)预测结果

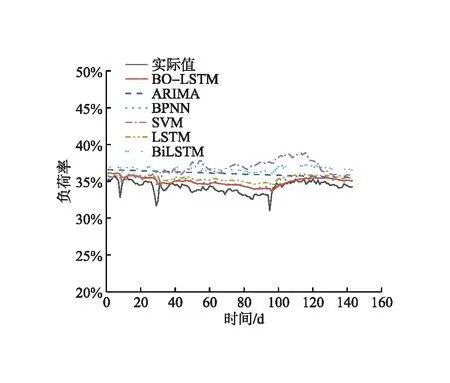
a)预测结果

a)预测结果

由图5～8可知,ARIMA和SVM模型的预测结果有明显偏差,其余模型均与实际值的历史走向相似。SVM模型的预测结果波动幅度较大,与Du Jian等人[23]给出的SVM模型善于捕捉数据的波动性相吻合。BPNN模型对历史数据的拟合效果较好,但对于有波动负荷率的预测效果不如LSTM模型,这是由于LSTM模型内部存在控制储存结构的模块,能较好地捕捉长期趋势的特征。另外,BO-LSTM模型的预测样本集中在残差最小[-5,5]范围内,说明测试样本的预测结果均接近实际值,且对于平稳型处理厂的优势最为明显。LSTM模型经贝叶斯优化后,弥补了参数造成预测波动的缺陷,减少了残差值较高的样本数,预测数据明显更贴近实际值。

表3 不同模型的预测误差表

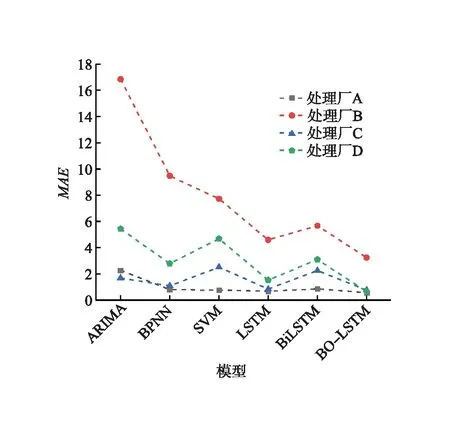
a)MAE结果对比

通过对波动型和平稳型天然气处理厂负荷率预测结果比较,可以得出BO-LSTM模型的预测精度和稳定性相较于传统时间序列预测模型具有显著提升,通用性较高。图10给出了天然气处理厂负荷率预测模型的预测结果,所有样本的预测数据与实际数据基本吻合,说明本研究的BO-LSTM模型能较好地捕捉因检修天数和日处理量等主要因素引起的时间特征,预测效果显著。

a)波动型

3 结论

本文对天然气处理厂负荷率预测开展研究,由于历史数据周期性较弱、数据量大,有一定的波动幅度,预测难度较高,现有研究未提出较好的预测模型。因此,本文基于数据的时间序列特性建立了BO-LSTM模型。为验证模型的准确性和通用性,选择了波动型(处理厂A、B)和平稳型(处理厂C、D)的天然气处理厂负荷率,并对比ARIMA、BPNN、SVM、LSTM和BiLSTM等传统预测模型以检验模型的优劣。

1)ARIMA、BPNN、SVM、LSTM、BiLSTM和BO-LSTM模型均可用于天然气处理厂负荷率预测。其中,预测效果最好的模型为BO-LSTM和LSTM。针对不同类型天然气处理厂,BO-LSTM模型能较好捕捉时间特征,天然气处理厂负荷率的预测精度最高,稳定性最强,处理厂A的MAE值和RMSE值分别为0.561和1.961,处理厂B的MAE值和RMSE值分别为3.242和10.316,处理厂C的MAE值和RMSE值分别为0.762和0.908,处理厂D的MAE值和RMSE值分别为0.643和1.373。与传统LSTM模型相比,预测误差MAE值和RMSE值最大可提升57.8%和30.1%。

2)本研究的BO-LSTM模型能够实现对天然气处理厂负荷率的实时预测和监控,可为天然气处理厂生产运行和决策提供技术支持。

3)传统LSTM模型的预测准确性和稳定性高于ARIMA、BPNN和SVM模型。因此,在LSTM模型基础上结合物理机理作进一步优化可实现更加准确的预测模型,未来可应用于电厂、水厂负荷率预测等领域。