强电磁脉冲环境下火箭尾段线缆皮电流计算

龙中权，赵 民，付继伟，陈 曦，梁 浩

（1.北京宇航系统工程研究所，北京，100076；2.中国运载火箭技术研究院，北京，100076）

0 引 言

强电磁脉冲对火箭系统的危害备受关注，火箭系统的抗强电磁脉冲指标是衡量火箭总体性能的重要依据。强电磁脉冲是一种瞬时电磁辐射，耦合进入箭上电子系统后，会对系统的硬件、软件及电路接口等造成严重的影响，可能导致整个系统工作异常，无法完成预定任务［1］。分析箭上的强电磁脉冲环境是箭上系统强电磁脉冲防护的基础，工程防护方法主要有屏蔽、滤波、限幅和接地等［2］。

火箭在起飞和级间分离后，火箭尾段中的线缆将暴露在空中，直接面临强电磁脉冲威胁。强电磁脉冲可以通过多种方式耦合进入火箭上搭载的各种电子电气设备，对敏感设备造成干扰，严重时可导致箭上关键设备工作异常，造成严重的后果。

本文分析了火箭尾段线缆的强电磁脉冲环境，采用时域有限差分法（Finite Difference Time Domain，FDTD）计算了尾段线缆在强电磁脉冲照射下的屏蔽层表面电流，研究了包括入射波极化方向、线缆长度、线缆布线高度在内的不同工况下电流分布特性，并对线缆上皮电流的波动性进行了探讨，为箭上尾段线缆的强电磁脉冲防护提供了有力支撑。

1 时域有限差分法

强电磁脉冲照射作用下线缆皮电流计算有多种方法，主要包括传输线法（Transmission Line Method，TLM）、有限元法（Finite Element Method，FEM）、矩量法（Moment Method，MoM）及时域有限差分法等。前3种方法主要在频率范围内进行计算，得出计算结果后需要进行傅里叶逆变换才可得到电流的时域特性；而时域有限差分法是在时域内计算，计算完成后可以直接得到线缆皮电流特性，相对方便。同时，时域有限差分法具有精度高、适用电大尺寸模型计算等优点［3-4］。

1.1 时域有限差分法的基本原理

FDTD 是一种直接离散时域Maxwell 偏微分方程组的方法，其核心思想是把带变量的Maxwell旋度方程转换为有限差分格式。在一个无源、各向同性、均匀且线性的空间中，Maxwell旋度方程可以表示为

式中 ∇为梯度算子；H为磁场强度；D为电位移矢量；J为电流密度；E为电场强度；B为磁感应强度；M为磁流密度。

以式（1）安培定律为例，经过离散化之后，可以得到离散后的安培定律为

且，

1.2 数值解的稳定性

FDTD 方程组是时间离散上的显示格式，为了保证数值解的稳定性，时间增量与空间增量需要满足一定的关系，即Courant稳定条件：

式中 Δx，Δy，Δz分别为三维空间x，y，z3个方向的空间步长；c为光速。

1.3 数值色散

数值色散是离散网格中电磁波的相速随着波长、传播方向以及网格分辨率变化而变化的现象，关于数值色散有如下关系：

式中ω为角频率；k为波数。当R=1时，空间差分和时间差分误差相互抵消，不存在色散误差；当R<1时，存在色散误差，且R越小，色散误差越大；当R>1 时，会导致复角频率出现，随时间增加波幅度按指数规律增加，即算法不稳定，从另一方面看，真实波前每时间步传播距离大于一个空间波长，这在数值空间中也是不可能的。

2 尾段线缆皮电流计算

2.1 尾段线缆强电磁脉冲环境分析

火箭飞行过程中，强电磁脉冲对敏感设备的影响主要包括传导干扰和辐射干扰。箭上包含的大量线缆是耦合强电磁脉冲的主要途径。在实际工程应用中，箭上线缆的布局需要考虑的因素较多，比如对质心、转动惯量等的影响，而对电磁环境的影响考虑较少。本文主要研究尾段线缆在火箭飞行工况下的强电磁脉冲环境，计算尾段线缆在入射场的不同极化方向、线缆离尾段底面布线的高度以及不同长度线缆上的感应皮电流，分析不同工况线缆皮电流的分布特性。

2.2 尾段线缆皮电流计算分析

2.2.1 计算模型及参数设置

利用时域有限差分法计算上述工况下火箭尾段线缆皮电流的分布特性，计算模型见图1。箭体尾段壳体的材料选用理想导电体，壳体直径为2 200 mm；发动机喷管前端直径为400 mm，后端直径为1 500 mm，高度为1 800 mm。线缆的屏蔽层直径为3 mm，屏蔽层为铜箔缠绕，铜箔厚度为0.2 mm，屏蔽层两端接地。激励为峰值50 kV/m的双指数平面波，其上升沿为2.5 ns，半宽高为23 ns，传播方向为-z轴方向。

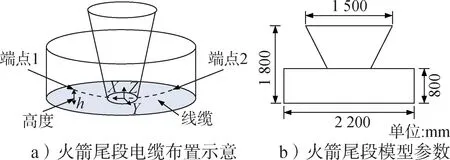
图1 火箭尾段模型及参数Fig.1 Rocket tail segment model and simulation parameters

2.2.2 不同极化方向的线缆皮电流计算

为探索强电磁脉冲的不同极化方向照射时对线缆上感应电流的影响，以x方向为基准，入射场分别选取x极化、30°极化、45°极化、60°极化、y极化、120°极化、135°极化、150°极化及180°极化进行研究。线缆环绕尾段底部布线，以坐标 （800，0，100）为起点逆时针画圆，布线半径800 mm，即线缆长度取2 512 mm，线缆离底面高度h取150 mm。

以入射波30°极化为例说明在不同极化条件下，线缆端点处感应电流分布特性，分别见图2、图3。

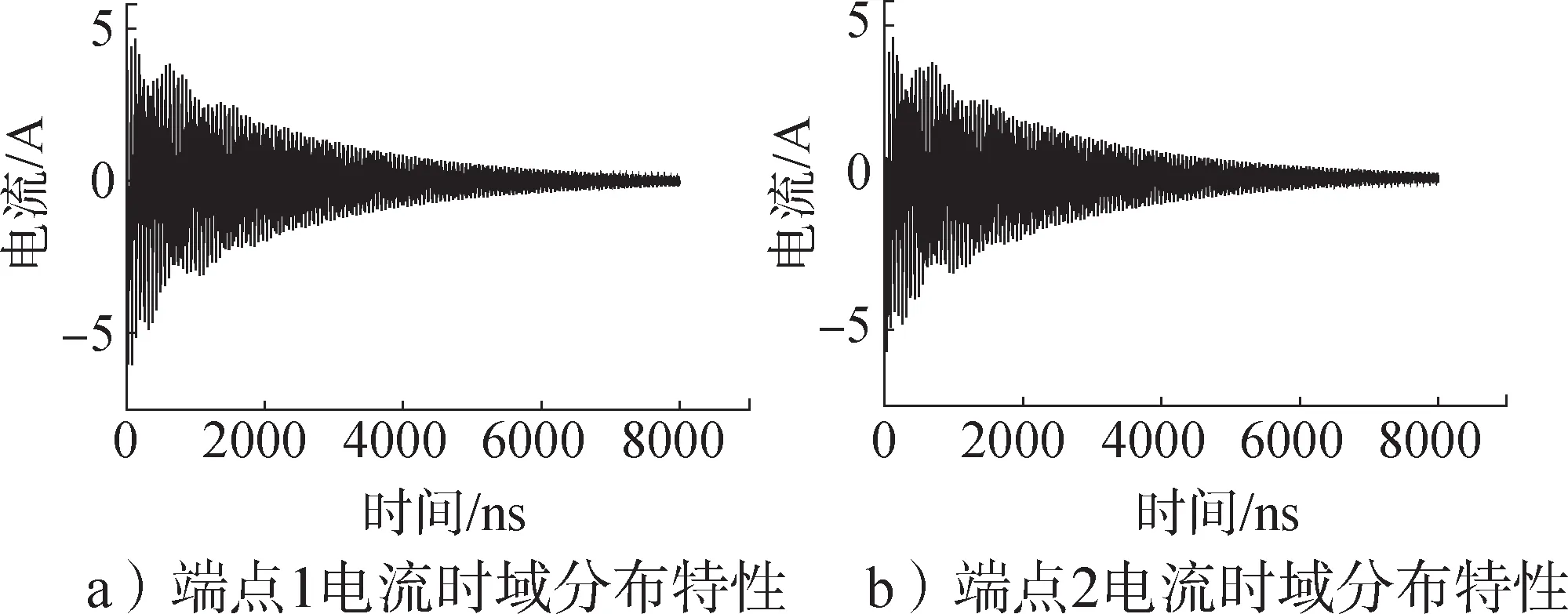
图2 30°极化方向时线缆端点处的电流分布Fig.2 Current distribution of 30 degree polarization at cable endpoints

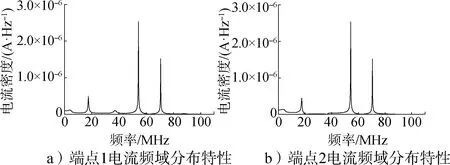
图3 30°极化方向时线缆端点处的电流频谱特性Fig.3 Current spectrum characteristics of 30 degree polarization at cable endpoints

在图2、图3中，端点1表示线缆旋转的起点，即坐标为（800，0，150），端点2 代表线缆另一端的终点。对上述各种极化方向下线缆端点处电流的分布特性进行计算，可以得到线缆端点处峰值电流与入射场极化角度之间的关系，如图4所示。

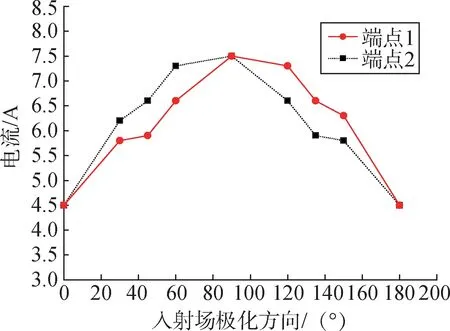
图4 线缆端点电流与极化角度的关系Fig.4 The relationship between current and polarization angle

从图4可以发现，线缆在电磁脉冲的照射下，线缆端点处感应的皮电流波形呈衰减振荡；对于30°极化方向，在100 MHz 的频率范围内包含3 个谐振频点，主谐振频率约为52.3 MHz。从图4可以得到，线缆端点电流在入射波为y轴极化方向时最大。

2.2.3 不同长度的线缆皮电流计算

为研究火箭尾段线缆皮电流分布与线缆长度的关系，入射波的极化方向分别选为x轴方向以及y轴方向，线缆离尾段底部的高度h取300 mm。

为获得不同长度的线缆，以坐标（800，0，300）为起点逆时针画圆，通过旋转不同角度得到不同长度的线缆。旋转的角度分别取30°（418.7 mm）、45°（667.6 mm）、60°（889.7 mm）、90°（1256.0 mm）、120° （1779.3 mm）、 135° （2001.8 mm）、 150°（2224.2 mm）以及180°（2512.0 mm）。在上述各种长度下，分析线缆端点在入射波x极化和y极化情况下产生的感应电流分布特性。

以90°旋转角度为例说明线缆上感应电流的分布情况，当入射波以x极化入射时，得到线缆两个端点的电流波形分别如图5、图6所示。

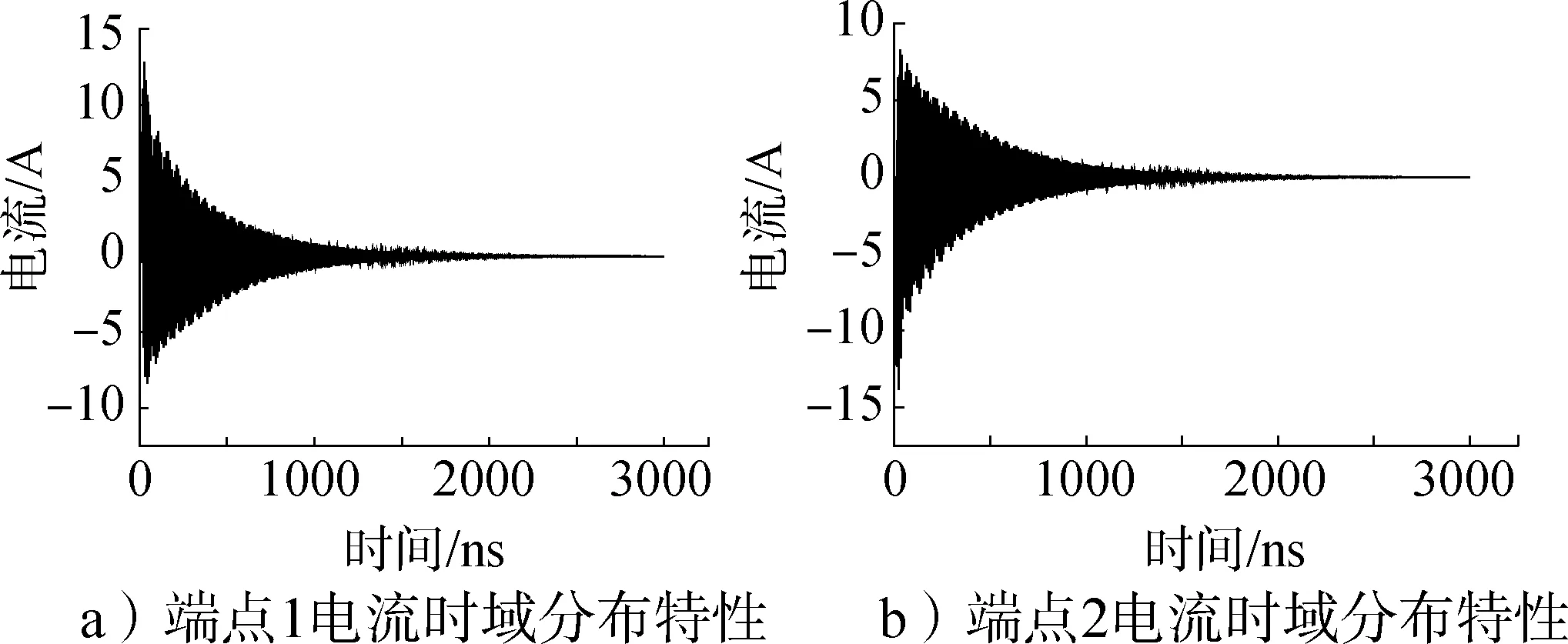
图5 x极化下线缆两端感应电流分布Fig.5 Current distribution of x-direction polarization at cable endpoints

图6 x极化下线缆两端感应电流的频谱Fig.6 Current spectrum characteristics of x-direction polarization at cable endpoints

计算上述各种长度电缆的端点处电流，得到在入射波分别为x极化、y极化条件下，各线缆端点处电流的分布，如图7所示。

图7 不同极化条件下，不同长度线缆端点处电流分布Fig.7 Current distribution at the endpoints of cables of different length under different polarization conditions

由图7可以发现，入射波无论在x极化还是y极化条件下，线缆两个端点皮电流的大小与线缆的长度没有明显的相关性。由后面的分析可以知道，这是由于线缆上皮电流的分布呈现了波动性，皮电流的大小与谐振频率以及线缆长度等因素有关，而并非由单一因素决定。

2.2.4 不同架设高度线缆的皮电流计算

为研究线缆布线离尾段底面高度对线缆屏蔽层感应电流的影响，选取线缆离壳体底面距离分别为100 mm、200 mm、300 mm、400 mm、500 mm、600 mm、700 mm几种工况进行计算研究。

选取线缆架设高度300 mm 为例说明一定高度线缆上感应电流的分布情况，当入射波以x极化入射时，得到线缆端点处电流的波形分别见图8、图9。

图8 x极化、300 mm高度时，线缆两端的感应电流分布Fig.8 Current distribution of x-direction polarization and 300 mm height at cable endpoints

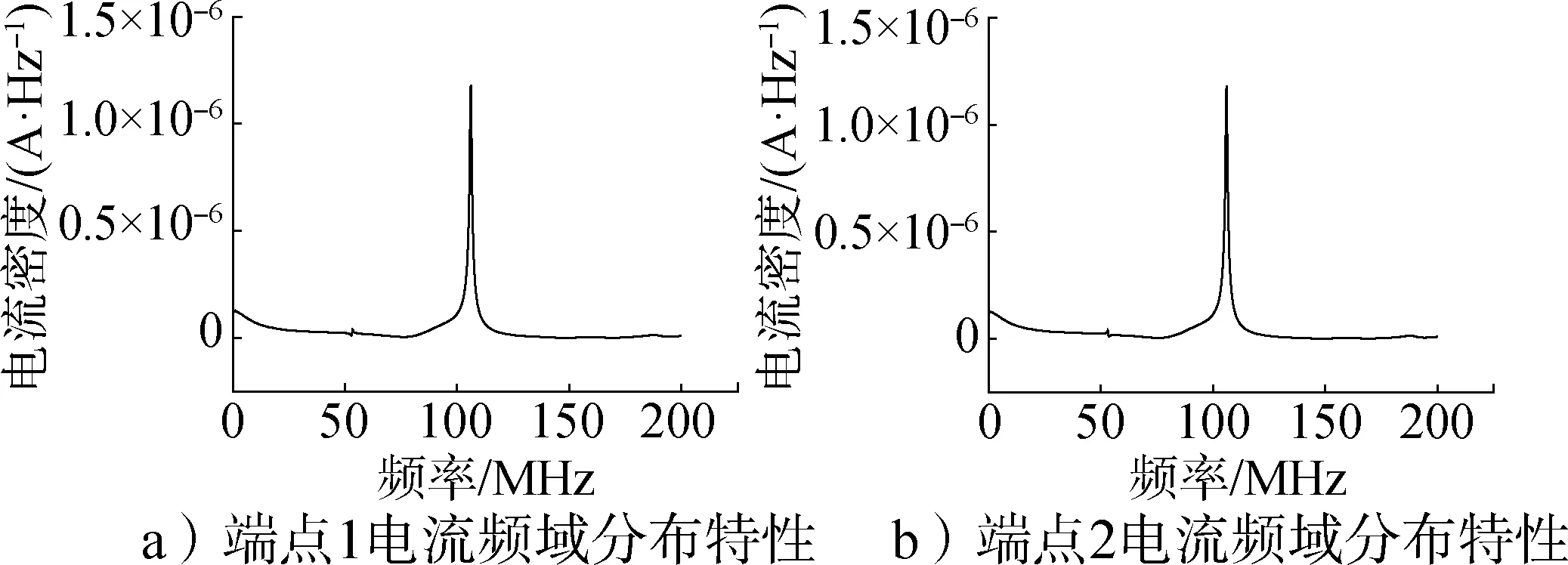
图9 x极化、300 mm高度时，线缆两端的感应电流频谱Fig.9 Current spectrum characteristics of x-direction polarization and 300 mm height at cable endpoints

针对不同架设高度、不同极化条件下线缆端点处峰值电流与布线高度的变化如图10所示。

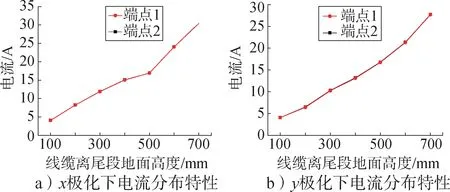
图10 不同极化条件下，线缆端点电流与架设高度的关系Fig.10 The relationship between cable endpoint current and installation height under different polarization conditions

结合图8、图9 可发现，线缆上的皮电流只有一个谐振峰，谐振频率约104.5 MHz，且在不同高度下，线缆谐振频率基本保持不变，说明线缆高度与谐振频率无明显相关关系。从图10可知，随架设高度的逐渐增大，无论入射波为x极化还是y极化，线缆端点的皮电流随着线缆离底面高度的增加而不断增大。

2.2.5 波动性分析

前面主要研究了线缆端点处皮电流的时域和频域分布特性，但是线缆其他位置处电流的分布特性未知。由于尾段线缆的长度较长，可与入射波波长相比拟，线缆上不同位置处的感应电流大小可能不同，所以有必要研究线缆上感应皮电流的分布特性。

以架设高度为300 mm，旋转角度为180°的线缆为例进行研究，分别计算30°、90°以及135°处的线缆皮电流，其特性如图11所示。

图11 不同位置处感应电流时域分布Fig.11 Current distribution at different positions

由上述结果可得，在线缆0°、30°、90°、135°处感应电流的峰值分别为：11.94 A、8.55 A、14.48 A、14.84 A，线缆上各处电流差异较大，说明线缆上皮电流呈现了波动分布。

2.2.6 结果分析

a）由图4中的感应电流与入射波极化方向的分析结果可以得到，不同极化条件下，线缆上感应电流分布各有差异，y极化时端点处电流达到最大。

b）由图7 中的感应电流与线缆长度的分析结果可以得到，无论入射波是何种极化，线缆上端点处的感应电流波形呈指数振荡衰减；而线缆端点处的电流峰值大小与线缆的长度没有明显的相关性，这是线缆上皮电流分布的波动性所致。

c）由图10 中的感应电流与不同布线高度的分析结果可以得到，无论何种极化，对于一定长度的线缆，其离底面的布线距离越高，线缆上端点处的感应电流越大，当线缆距离底面700 mm 时，线缆上的感应电流达到了30.4 A。

d）从图11 关于线缆不同位置处电流分布的研究可发现，不同位置处线缆的皮电流峰值存在较明显差异，这是由于感应电流在线缆上的分布呈现了波动性。

3 结束语

通过分析火箭尾段强电磁脉冲环境，采用时域有限差分法计算了尾段线缆的皮电流。从计算结果可以看出，在强电磁脉冲辐照下，无论何种极化，线缆皮电流波形为指数衰减振荡型；随着线缆布线高度增加，线缆端点处皮电流显著增加，所以在实际工程中，线缆布线应该尽量靠近尾段底部；线缆端点处皮电流的大小与线缆的长度没有明显的相关性；同时，尾段线缆皮电流的分布呈现了波动性，线缆不同位置处线缆的皮电流峰值大小差异较大。本文研究结果为火箭箭上的强电磁脉冲防护设计提供了有益参考。