高速铁路无砟轨道大跨斜拉桥成桥预拱度设置方法

刘本永，严爱国，李世伟，李的平，朱胜阳，李若愚，杨得旺

(1.中铁第四勘察设计院集团有限公司，湖北 武汉 430063；2.中铁二十三局集团有限公司，四川 成都 610031；3.西南交通大学 轨道交通运载系统全国重点实验室，四川 成都 610031)

高速铁路桥梁采用无砟轨道,既可更好满足速度为350 km/h的高速行车需求,也能减轻桥面系重量,具有耐久性好、养护维修工作量小、有效避免道砟飞溅等特点,在高速铁路工程中得到广泛应用[1-2]。目前我国在中小跨径桥梁上铺设无砟轨道已有成熟的工程经验,对于大跨铁路桥梁而言,相关工程经验不足,理论研究也不完善[3]。

随着服役年限的增加,在列车荷载、环境温度等往复作用下,由于混凝土收缩徐变效应、结构力学性能退化等,大跨铁路桥梁的变形逐渐增大。当桥梁累积变形超过轨道扣件允许的调整范围时,将对轨道平顺性产生危害,甚至导致轨道扣件破坏失效,增加维养难度,成为列车安全运营的隐患[4-5]。桥梁预拱度会抵消部分列车荷载产生的下挠变形,可改善无砟轨道结构的受力和列车运行的线路平顺性。高速铁路无砟轨道大跨桥梁需设置合理的成桥预拱度。

大跨桥梁的预拱度控制了无砟轨道的线形,无砟轨道的线形理论上应符合TB 10621—2014《高速铁路设计规范》[6]规定的轨道静态铺设精度标准,即基于矢度差法,当弦长为300 m时,相距150 m的任意两测点实际矢度差与设计矢度差的偏差不得大于10 mm。但现有的大跨桥梁很难满足此要求,以昌赣铁路赣江特大桥(主跨300 m的无砟轨道斜拉桥)为例,在列车静活载作用下,桥梁主跨跨中下挠59.8 mm,参考TB 10091—2017《铁路桥梁钢结构设计规范》[7],成桥预拱度与1/2静活载所产生的挠度曲线基本相同,但方向相反,考虑收缩徐变效应影响,该桥的跨中预拱幅值应大于30 mm,此时最大的矢度差等于跨中预拱幅值,远超10 mm的限值。值得注意的是,根据目前大跨度桥梁运营的情况,如天兴洲、安庆、黄冈、铜陵长江大桥等,温度作用下轨道竖向位移均远大于10 mm,但这些桥均表现出良好的舒适性和安全性。因此,将这一标准机械地套用在大跨桥梁上是值得商榷的,或者说该项条文在大跨桥梁上的适用性尚需专门研究[8-9]。相关问题已成为制约无砟轨道在大跨铁路桥梁上应用的技术瓶颈。

鉴于此,本文提出一种适用于高速铁路无砟轨道大跨斜拉桥成桥预拱度设置的新方法。首先,提出合理成桥预拱度的计算方法和应满足的基本指标,然后,以昌赣铁路赣江特大桥为例,基于车-线-桥耦合振动分析模型,分析设置预拱度与否对桥梁结构长期使用性能演变的影响,以验证所提方法的可靠性。

1 成桥预拱度线形确定方法

成桥预拱度的设置主要是为了消除运营过程中列车活载、收缩徐变等对桥面线形的影响。

1.1 考虑列车静活载影响

当列车驶过桥跨结构时,会引起桥梁结构变形,通常将半个静活载产生的挠度曲线作为预拱度曲线,但方向相反。对于双线及多线铁路,鉴于列车在桥上交会或并行的概率较小,取单线列车的静活载计算预拱度。

1.2 考虑收缩徐变效应影响

收缩徐变效应会随时间不断加剧桥梁结构的变形,通常在10 a后收缩徐变变形趋于稳定。在设置抵消收缩徐变引起的下挠变形的预拱度时,如果直接按抵消10 a后的变形设置,则成桥初期会上拱过大,不利于行车;但如果预拱度设置过小,将不足以抵消收缩徐变变形,也不利于行车。

收缩徐变引起的桥梁变形幅值随时间的变化示意见图1。收缩徐变引起的桥梁变形并非均匀变化的,随着服役时间的增加,变化趋于平缓。设置抵消收缩徐变变形的合理预拱度可取10 a收缩徐变变形幅值的算数平均值,使设置的预拱度幅值与每年变形幅值之差δi(i=1,2,…,10)的平方和最小。预拱幅值函数f(A)可表示为

图1 收缩徐变变形幅值随时间变化示意

(1)

(2)

式中:A为收缩徐变变形幅值;an为第n年收缩徐变引起的变形幅值。

综上,预拱度函数Dc为

(3)

式中:Dl为列车静活载产生的全桥线形下挠值;Dcs为考虑10 a的收缩徐变作用引起的全桥线形下挠,幅值为A。

通常情况下,按式( 3 )计算得到的预拱线形并不光滑,需采用样条曲线或三角函数对其拟合以满足无砟轨道铺设及高速平顺行车的要求,为此,提出合理成桥预拱度应满足的基本指标。

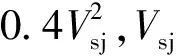
(2)60 m弦长的弦测偏差不超过8 mm

根据TB 10601—2009《高速铁路工程测量规范》[10]对无砟轨道几何形位的要求,需对轨道的中波与长波不平顺进行检测,直接将矢度差法应用于大跨度桥梁往往会导致大幅超限。文献[11]通过对比动检车实测数据和仿真计算结果发现,基于弦测法,采用60 m弦长输出的轨道不平顺与车体加速度存在很好的相关性,且将对应的弦测容许偏差控制在8 mm内时,车体加速度不会出现Ⅰ级超限。因此,提出将60 m弦长的弦测容许偏差不超过8 mm作为预拱线形应满足的第2个基本指标。

弦测法是以一定长度的直线为基线,以基线中点到轨面的矢距为测量值,见图2。图2中,线段AB为弦测基线,用L表示;点C为基线中心,点C的弦测矢量值为CD,用M表示;CD′为C点与轨道相交的竖直线。由于M/L很小,可近似认为|CD|=|CD′|,可得

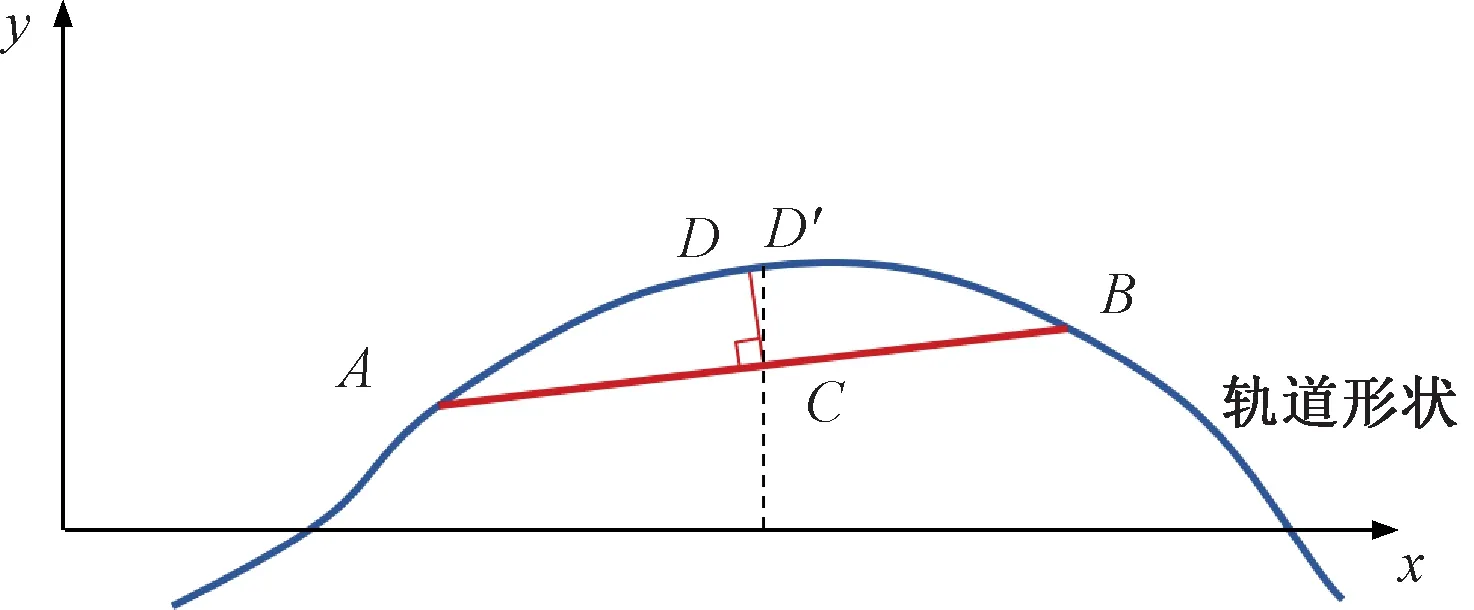
图2 弦测法示意

(4)

式中:yi为各点竖坐标,i表示A、B、D′点。

2 工程实例

为验证本文提出的预拱度设置方法,以昌赣客专赣江特大桥为例,计算该桥的合理预拱度线形,建立车-线-桥耦合振动分析模型,研究预拱度的设置对桥梁长期使用性能的影响,以验证预拱度度设置方法的可靠性。

昌赣高速铁路赣州赣江特大桥全长2.156 km,主跨长300 m,是世界上跨径最大的高速铁路无砟轨道桥梁之一,轨道为CRTSⅢ型,设计速度为350 km/h。主梁边跨及部分中跨主梁为预应力混凝土箱梁,其余中跨主梁为箱形钢-混凝土结合梁,桥塔为人字形混凝土桥塔。

2.1 合理预拱度设置

为准确分析桥梁在车辆活载和收缩徐变作用下的变形,采用通用有限元分析软件Abaqus建立全桥精细化三维仿真分析模型,见图3。图3中,斜拉索采用多段并联单元模拟,每根斜拉索由6个杆系单元(T3D1)和6个梁单元(B31)并联而成,全桥共计1 152个单元;边跨混凝土主梁和中跨钢箱组合梁的混凝土板均用实体单元C3D8模拟,以充分考虑剪力滞后效应,边跨混凝土梁共367 424个单元,混凝土板共83 200个单元;钢梁用板单元S4模拟钢箱梁,共210 080个单元;钢梁和混凝土板之间的连接采用弹簧单元模拟,共18 792个单元;在处理钢-混结合段时,将伸出的钢梁单元嵌入到混凝土单元中;桥塔同样采用实体单元C3D8模拟,以充分考虑桥塔受力的空间特性。

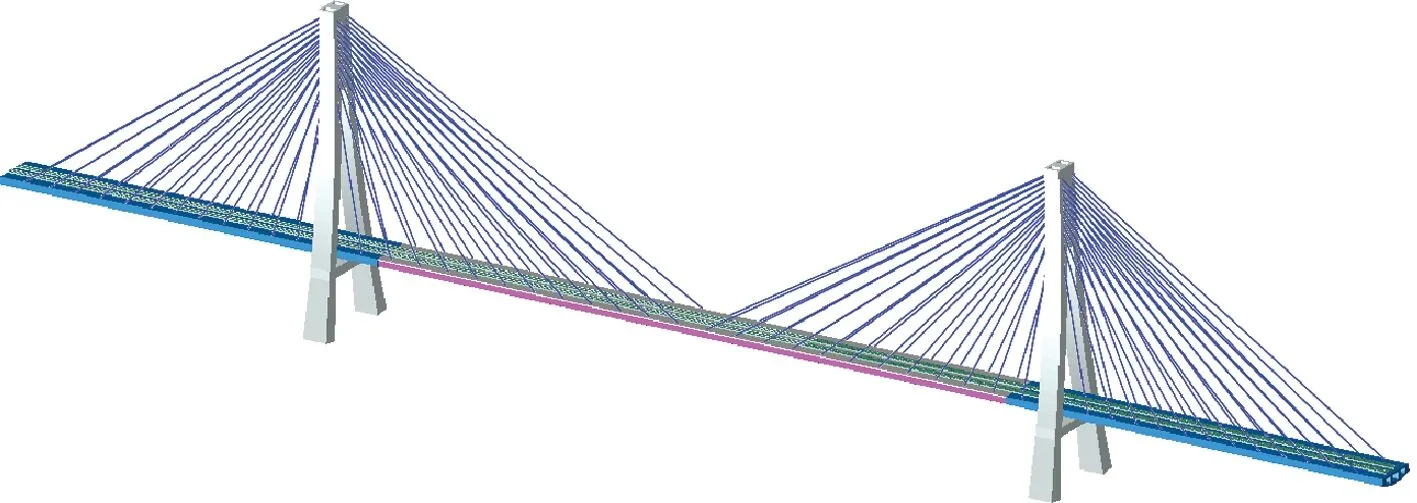
图3 有限元分析模型

在施工阶段分析中,采用“追踪单元”沿主梁切线方向激活新单元,采用“迭代降温法”施加斜拉索目标索力,采用“生死单元”实现斜拉索与主梁节段的激活与钝化。收缩徐变的影响采用文献[12-13]提出的混凝土三维收缩徐变分析模型计算。

(1)考虑列车活载的预拱度

根据建立的有限元分析模型,在列车静活载作用下,桥梁主跨跨中产生了向下幅值为59.8 mm的变形,因此,考虑列车活载影响的预拱度幅值为30 mm。

(2)考虑收缩徐变效应的预拱度

成桥后10 a内的收缩徐变引起的梁体下挠见图4。按式( 2 )计算得到收缩徐变预拱度幅值为52 mm。

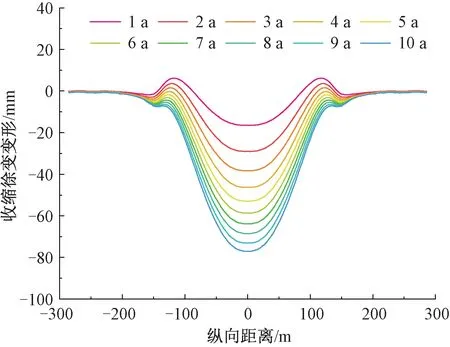
图4 成桥10 a内桥梁收缩徐变变形

最终考虑列车静活载和收缩徐变作用下的合理预拱曲线与单一荷载的预拱度曲线具有相同的谐波波长,半波长为150 m。设置坐标原点为桥梁主跨跨中位置,直接将单一荷载的预拱度曲线幅值(82 mm)相加,即可得到合理预拱曲线的表达式为

(5)

合理预拱曲线见图5。图5中,黑色曲线为考虑2种因素的合理预拱度曲线。

图5 合理预拱曲线

(3)合理预拱度判断指标

根据式( 5 )确定全桥预拱线形后,叠加成桥后10 a内收缩徐变引起的梁体下挠,即可得到设置预拱度后桥梁线形的变化情况,由此可计算10 a内桥梁线形的最小曲率半径和60 m基线高程弦测偏差值,以判断是否满足合理预拱度指标。最小的曲率半径随时间的演变规律见图6,60 m弦长对应的弦测偏差计算结果见图7。结果表明,桥梁在不同服役时期的线形最小曲率半径均大于0.4Vsj2(49 000 m),弦测偏差均小于8 mm。

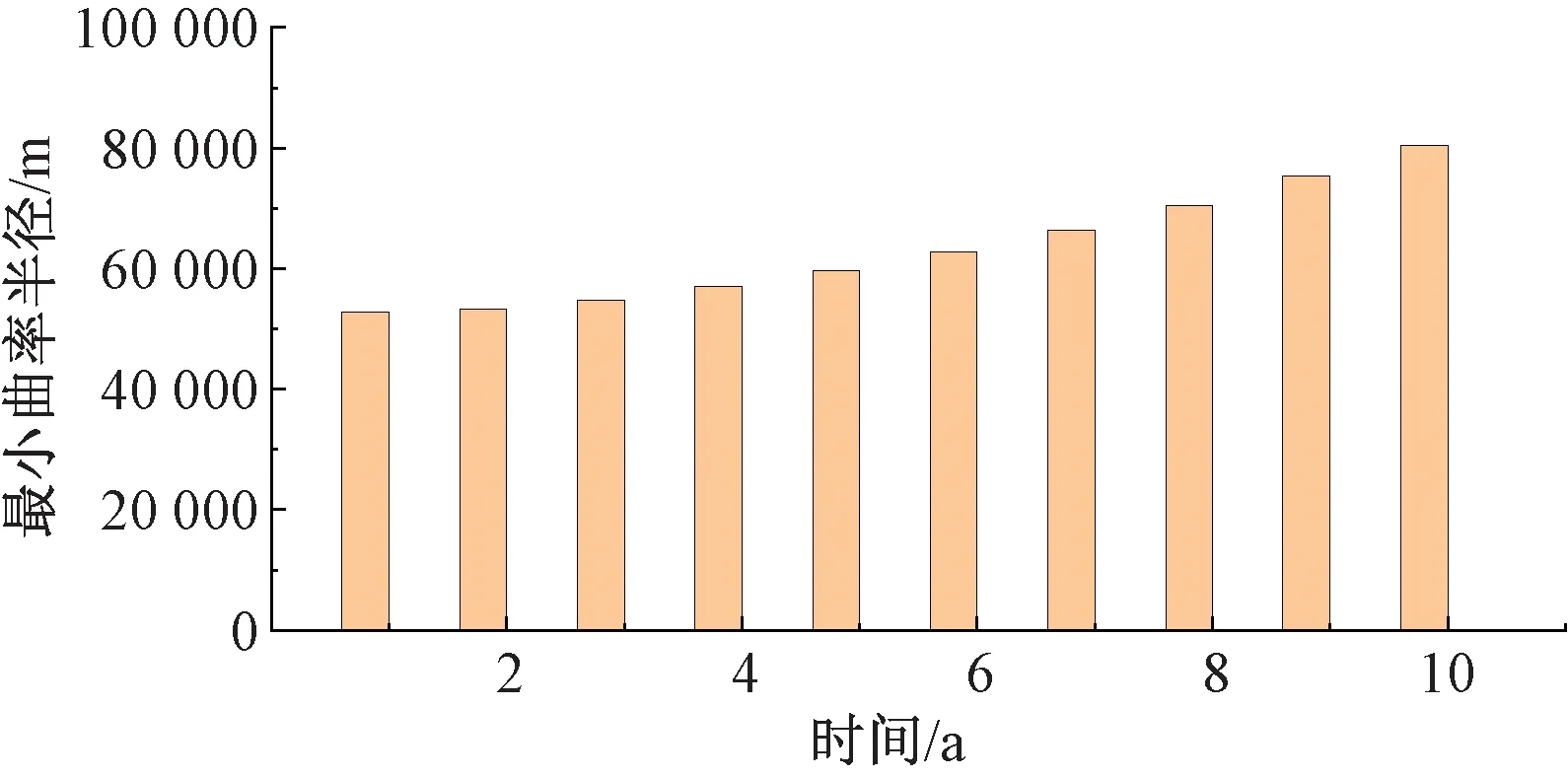
图6 桥梁线形最小曲率半径随时间演变

图7 60 m基线弦测偏差值

2.2 基于车-线-桥耦合分析的预拱度设置方法验证

为验证所提成桥预拱度设置方法的合理性,基于西南交通大学自主开发的车-线-桥动力学分析软件TTBSIM,建立车-线-桥耦合振动分析模型,见图8。

图8 列车-轨道-桥梁动态相互作用模型示意

车辆模型基于CRH380B列车建立,由车体、构架及轮对共7个刚体以及一、二系悬挂组成。每一个刚体考虑垂向、横向、侧滚、摇头、点头共5个运动自由度,因此,每一车辆共有35个自由度,车辆参数见文献[14-15]。

对于无砟轨道模型,建模时将左右两股钢轨均视为离散弹性点支承基础上的无限长Euler梁,并考虑其垂向、横向及扭转自由度,而道床板则采用板桥壳模型模拟,见图9。轨道结构参数见文献[16]。

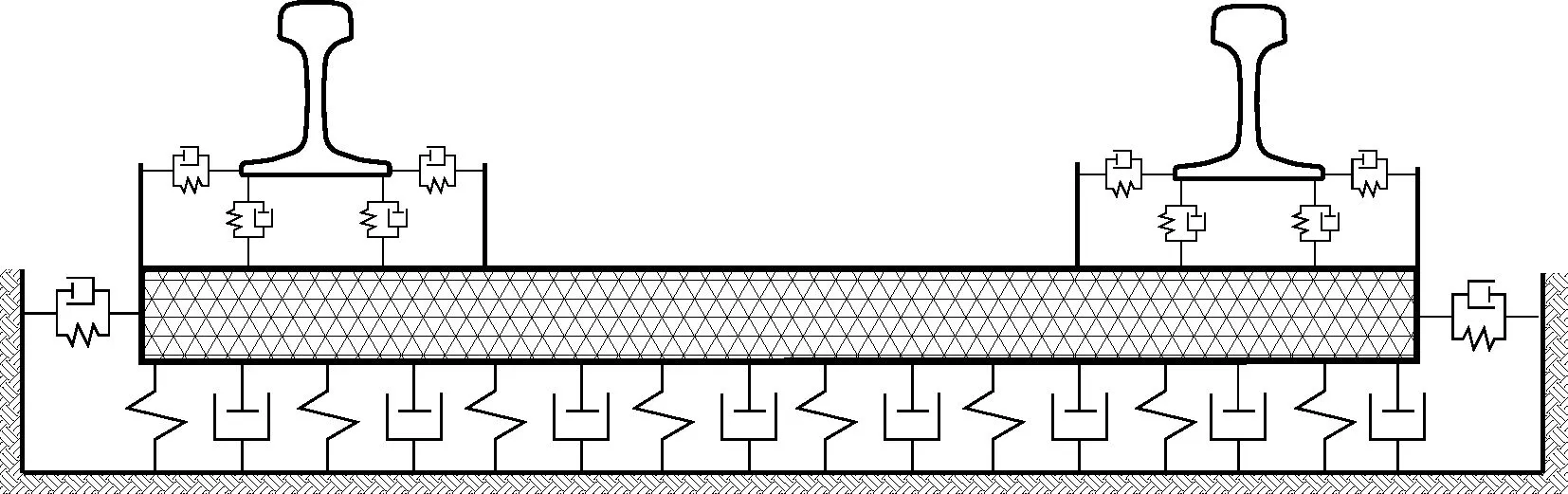
图9 无砟轨道动力学模型

桥梁模型采用TTBSIM提供的单元库建立,主梁用“梁格法”模拟,斜拉索用杆单元模拟,桥塔、桥墩等结构采用梁单元模拟。

在分析软件TTBSIM中,车轨及桥轨相互作用模型的建立过程参考文献[17]。列车速度为350 km/h,对比分析预拱度设置与对桥梁长期使用性能的影响。

根据成桥10 a内的收缩徐变引起的桥梁变形,依次计算在第1～10年的收缩徐变变形的影响下,设置和不设置预拱度2种工况的系统动力学响应。提取车体垂向加速度、桥梁中跨跨中垂向加速度、脱轨系数以及轮重减载率4个动力学指标进行对分析。

成桥10 a内2种工况的各动力学指标幅值对比见图10。成桥后第10 a时,2种工况的动力学指标时间历程对比见图11。

图11 有无预拱度的动力学指标时间历程对比

由图10、图11可知,随着服役时间增长,预拱度的设置降低了车体垂向加速度、轮重减载率,且服役时间越长,效果越显著。在成桥10 a后,车体垂向加速度较不设预拱度降低约67%,轮重减载率降低约18%;桥梁中跨跨中垂向加速度仅在成桥初期有少量差异,且随时间差异减小;而预拱度的设置对脱轨系数几乎没有影响。

综上可知,混凝土收缩徐变会使行车平稳性出现较大差异,按本文所提方法设置的预拱度可显著降低车体垂向加速度和轮重减载率,明显改善车-线-桥系统动力学性能,对提高运行平稳性具有重要意义。

3 结论

本文提出了高速铁路无砟轨道大跨斜拉桥考虑桥梁收缩徐变的成桥预拱度设置方法和合理预拱度的判断指标,并基于列车-线路-桥梁耦合振动动力仿真分析结果验证所提方法的可靠性,得到如下结论:

(1)相较于传统不考虑收缩徐变的成桥预拱度,本文所提方法得到的预拱度幅值是传统方法的2倍多,表明将传统预拱度设置方法用于大跨度桥梁时会明显低估成桥预拱度幅值。

(2)基于本文所提方法,在满足线路竖曲线最小曲率半径限值和60 m弦长弦测容许偏差限值的前提下,设置预拱度可降低车体垂向加速度和轮重减载率,使车-线-桥系统获得更好的动力学性能,对提高车辆运行平稳性具有重要意义。