基于BP的随机混合生产前沿面模型

路世昌, 刘雨诗, 于智龙, 刘 舒

(1.辽宁工程技术大学 工商管理学院,辽宁 葫芦岛 125000; 2.中国银行保险监督管理委员会铁岭监管分局,辽宁 铁岭 112000)

0 引言

数据包络分析(DEA)通过对多投入多产出决策单元建模,构建具有凸性、锥性及最小性的生产集合,再确定决策单元的包络面,即生产前沿面,决策单元与生产前沿面之间的距离为无效部分,决策单元在生产前沿面上的投影为最有效的投入产出组合,从而估计决策单元的效率值。作为非参数多产多投模型,DEA模型及其扩展模型避免了对生产效率函数具体形式的依赖性,在解决实际问题时更具有普适性和实用性,被广泛应用于政府效率评估[1,2]、银行效率评估[3,4]、保险业效率评估[5]等多个领域,相关论文数量成指数级上升趋势。然而,DEA模型基于确定性假设构建生产前沿面的过程中,忽略了模型中噪音、随机误差和环境变量等不确定因素,而实际的生产集合由非理论数据构成,常带有误差等其他干扰项,因此在使用DEA模型估计实际生产集合的效率时,生产前沿面极易受到特异数据影响而偏移。

针对这一问题,学者们从不同角度给出了解决办法。马生昀等[6]利用随机规划方法构建了参数或决策单元服从一定概率分布的DEA随机扩展模型,王美强和李勇军[7,8]利用模糊数学方法量化非确定性变量构建DEA模型,在模糊环境下形成模糊生产前沿面,KUOSMANEN等[9]和谢辉军等[10]通过DEA模型与随机前沿面分析(SFA)结合的方式进行数据分析,增加模型的随机性。上述方法中,随机规划方法需依赖于特定参数或概率分布,模糊数学方法中模糊数的转化效果直接影响模型效率评估结果,在与SFA结合的方法中只能将误差归因于一个投入或一个产出变量上。

近几年,由于机器学习算法在处理不确定性问题上具有一定优势而成为数据处理的主流方法,将DEA模型与机器学习算法结合使用,能够实现对具有多重特征且不确定性数据的分析,减少对特定参数或概率分布的依赖,形成具有可扩展性的集成模型。其中,神经网络算法在处理多维、复杂数据上具有优势,在与DEA模型结合时效果更为突出,被越来越多的学者选择使用[11,12]。目前在DEA模型与神经网络算法结合的方法中,一般选用投入或产出数据作为自变量,已生成的效率值作为因变量,进行回归分析,实现效率值的校正,模糊了DEA模型中包络面与决策单元之间的关系。冯长敏等[13]根据DEA模型中决策单元在生产前沿面上的投影值,利用BP神经网络重新估计生产前沿面并实现了决策单元的排序。但仅通过决策单元有效值进行再估计,极大的依赖原有生产前沿面,易受到特异数据影响。

本文考虑构建一种随机混合生产前沿面(BP_SHPF)模型,将有效决策单元与贴近生产前沿面的无效决策单元分组混合,通过BP神经网络训练,确定新的生产前沿面位置,并根据新建立的生产前沿面估计决策单元效率值。BP_SHPF模型通过BP神经网络避免了非机器学习方法的局限性,同时保留了决策单元与生产前沿面的位置关系,校正了生产前沿面前置问题,在对实际生产集合进行效率评估时得到更易区分、更合理的决策单元效率值与效率排序。

1 BP_SHPF模型

BP_SHPF模型流程如图1所示,主要包括以下4个步骤:求解确定生产前沿面;混合有效单元与无效单元;神经网络训练;重新计算决策单元(DMU)效率。

1.1 DEA模型求解确定生产前沿面

BP_SHPF模型作为一种集成模型,适用多种DEA模型。本文将以DEA模型中的BC2模型为例说明BP_SHPF模型的构建方法。BC2模型能够在变动规模报酬下实现纯技术效率与规模效率的评估,其生产可能性集为pB={(x,y)|x≥Xλ,y≤Yλ,eλ=1,λ≥0},其中,条件eλ=1为凸性约束条件,减少了模型的可行域范围。

下面以面向产出的BC2模型为例:

(BCC-O0) maxηB

s.t.Xλ≤x0

ηBy0-Yλ≤0

eλ=1

λ≥0

如图2所示,BC2模型构建了生产前沿面A-B-C,生产前沿面上的决策单元为有效单元,效率值为1,其他无效决策单元在生产前沿面上的投影为该决策单元的有效值,BC2模型中投影值计算如下所示:

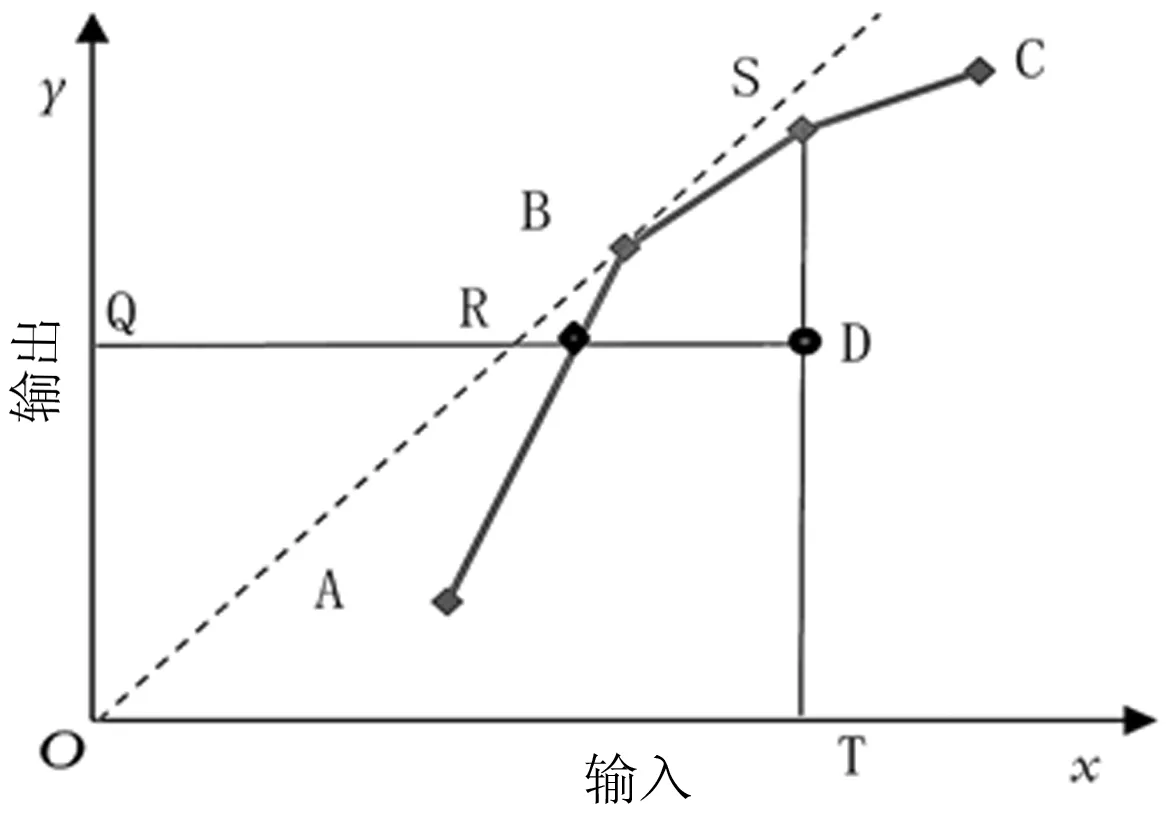
图2 BC2模型生产前沿面

根据投影值可计算决策单元效率,公式如下:

BCCefficiency=DT/ST

1.2 混合决策单元

如图3所示,BP_SHPF模型为增加DEA模型随机性,减少特异数据影响,认为位于生产前沿面附近的决策单元仍有一定概率是有效决策单元,将这些决策单元与有效决策单元混合,重新生成生产前沿面,将一定程度改善DEA模型生产前沿面前置情况。

图3 特异数据影响生产前沿面

在投入集合X中,投入相近的决策单元的效率评估应采用同一参考标准,因此本文将采取分段最优方法进行数据混合,算法过程描述如下:

(1)将投入集合X按序均分为N个子集合记为Xn,并将子集中包含最多的有效决策单元数记为m。

(2)对第n个子集内的决策单元按效率降序排列,取效率最大的m个决策单元,标记为混合单元集合S。

(3)计算各子集中混合决策单元平均效率Pn,比较求得全部子集的最低混合决策单元效率P′。

(4)对任意非最低效子集Xn,将效率降序排序m+1至m+a个决策单元添加至集合S,使得Pn≤P′且S是Xn内决策单元效率均值最大的子集。

1.3 BP神经网络训练

本小节将混合决策单元集合的投入值作为输入,产出值作为输出,进行BP神经网络训练,通过误差反向传播进行各层神经元参数调整,实现集合X的期望产出值估计。BP神经网络最终目标是误差最小化,通常采用梯度下降算法,按误差梯度反向调整神经元参数,一定程度存在无法获得全局最优、学习效率低、收敛速度慢及理论依据不足等问题。为此许多学者提出了BP神经网络优化方法,包括随机梯度下降、拟牛顿法、自适应梯度算法、共轭梯度法等。本文采用自适应梯度算法训练神经网络,学习速率根据误差大小调整,无需设定,使神经元参数向误差减小方向调整,算法过程简述如下:

1)构建BP神经网络net包括X个输入,H个隐藏单元,Y个输出;

2)初始化神经网络权值w;

4)与n-1次迭代误差进行比较,若E(n)E(n-1)则减小学习步长η(n)=η(n)×b,b∈(0,1);

5)net权值与步长η(n)存在以下关系w(n+1)=w(n)-η(n)×(δE(n)/δw(n));

6)重复步骤1至步骤5直到误差值小于预设误差或实验迭代次数满足要求。

BP_SHPF模型中神经网络结构如下:

神经网络层数:多位研究学者通过理论及实践得出,具有单隐藏层的BP神经网络能够逼近闭区间的任意连续函数,因此BP_SHPF模型使用如图4所示的“输入层—隐藏层—输出层”三层结构神经网络训练数据集。

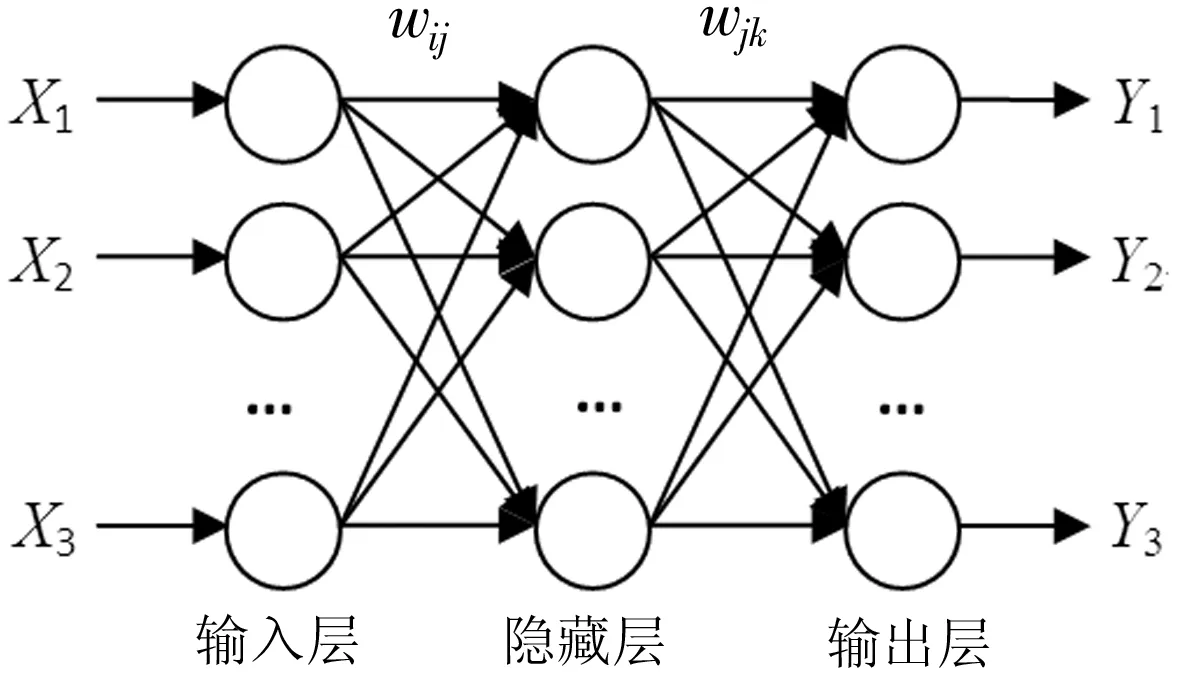
图4 三层结构神经网络

输入输出节点数:神经网络模型目标是校正生产前沿面位置,输入、输出结点数应与DEA模型中投入、产出数相对应。

隐藏层节点数:隐藏层节点数是直接影响神经网络准确性的重要参数,对于三层神经网络结构而言,隐藏节点数H过大会导致过拟合,H过小会导致误差较大。本文假定隐藏层节点与训练样本数量和输入输出数存在以下关系:

其中,H为隐层节点数,X为输入个数,Y为输出个数,a为常数[1,10]。在实验过程中对a取1至10的整数,计算对应的H值,并分别进行神经网络训练,计算每次训练对应总误差Ea,比较Ea大小,选取Ea最小时的H值作为实际隐层节点数。

1.4 决策单元效率再计算

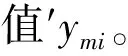
决策单元m的实际产出值与生产前沿面上产出值的距离为该决策单元的无效部分。如图5所示,在DEA模型中决策单元的效率通过原生产前沿面A-B-C-D上的投影点F计算,在BP_SHPF模型中构建了新的生产前沿面A-B-E-D,决策单元m的效率通过投影点G计算。

2 实验结果

2.1 Monte Carlo模拟

本节通过Monte Carlo模拟对BP_SHPF模型分别进行单产单投及多产多投验证。

(1)单产单投模型

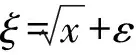
实验中随机生成两个样本数据,数据大小分别为N=100,N=300,重复实验次数M=100,实验结果如图6、图7所示。其中,“*”为DEA模型生成的前沿面,“+”为DEA_BP模型,即BP仅对有效决策单元校正结果,“◆”为BP_SHPF模型生成的前沿面,“▲”为计算目标值ξ,折线为实际目标值′ξ,可以发现DEA模型前沿面存在明显前置,DEA_BP模型增加了前沿面的随机性,但并不能有效校正前沿面,甚至出现有效值高于DEA模型的情况,而BP_SHPF模型通过生成光滑非线段构成的生产前沿面,有效的校正其前置问题,更贴近真实情况。

图6 N=100投入产出估计结果

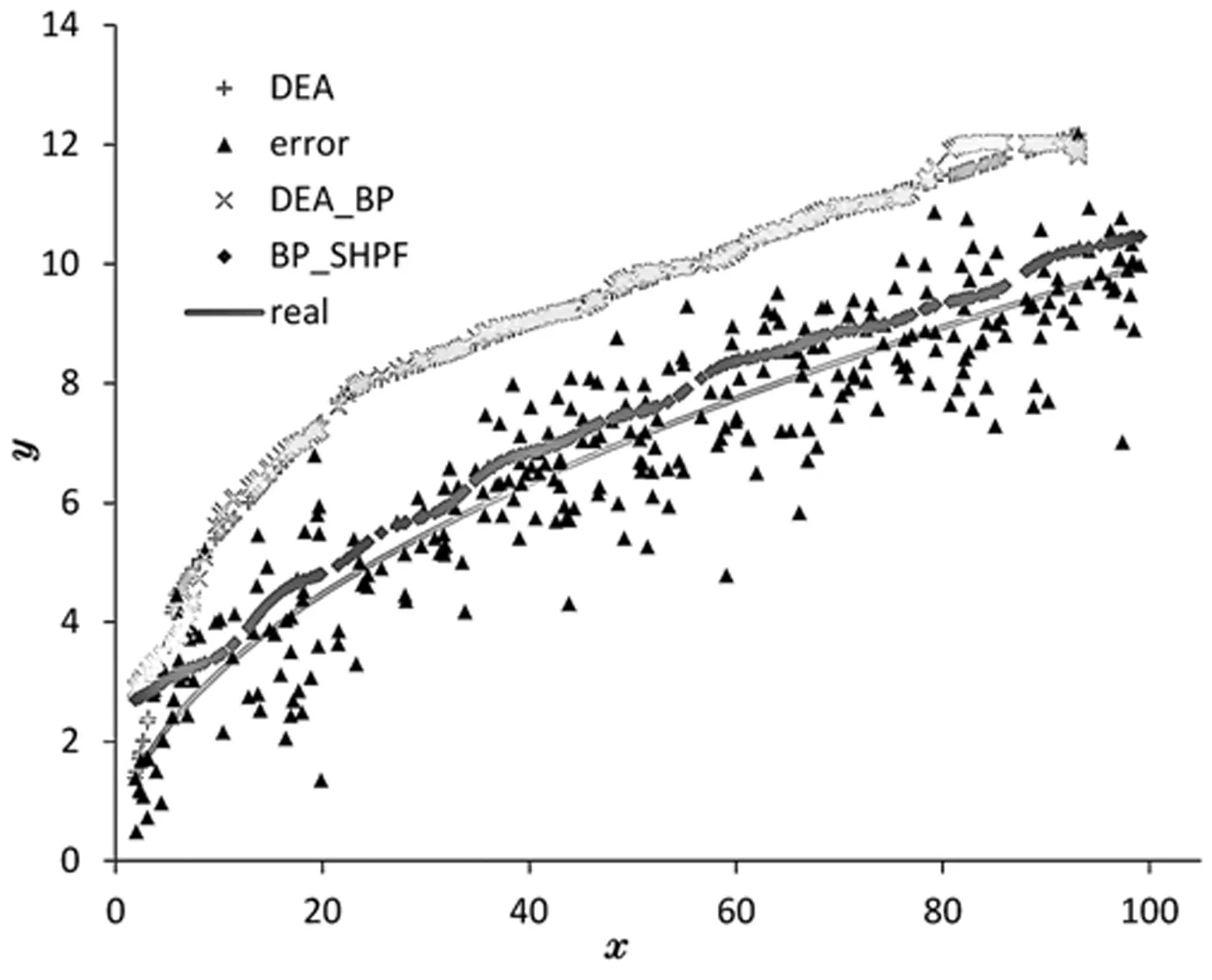
图7 N=300投入产出估计结果

模型误差结果比较如表1、表2所示,表中E为各模型误差均值,MSE为均方误差,BIAS为偏差。对比表中结果可以发现,BP_SHPF模型MSE和BIAS均明显小于DEA和DEA_BP模型,BP_SHPF模型一定程度上有效,且样本数量N=300时BP_SHPF模型MSE和BIAS值小于N=100,说明随着样本数量增加,BP_SHPF模型估计效果有所提升。

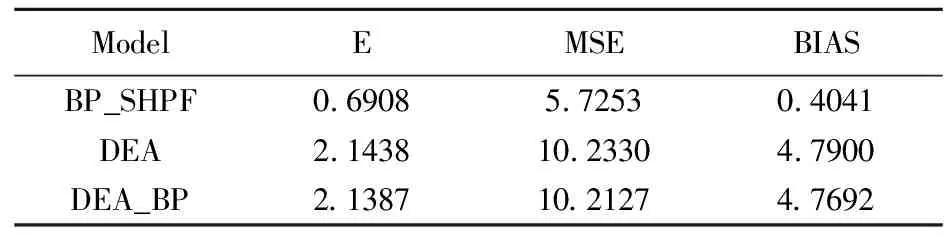
表1 N=100单产单投E、MSE、BIAS值

表2 N=300单产单投E、MSE、BIAS值

(2)多产多投模型

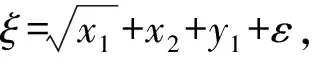
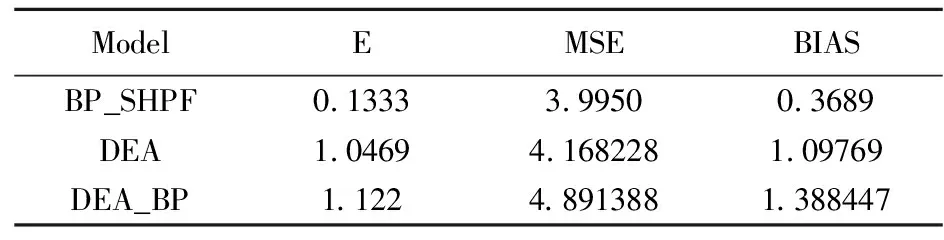
表3 N=100多产多投E、MSE、BIAS值

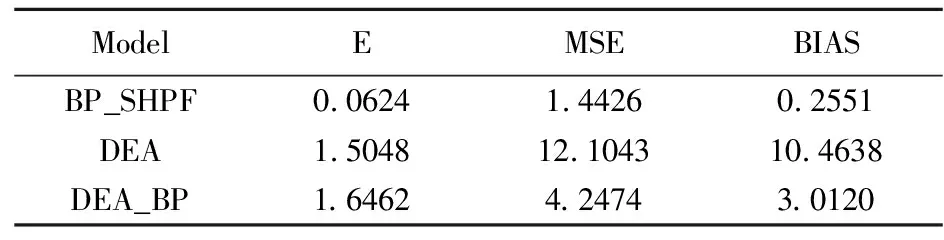
表4 N=300多产多投E、MSE、BIAS值

2.2 Spearman 秩相关分析

本节通过Spearman秩相关分析验证BP_SHPF模型计算的效率值与传统DEA模型计算的效率值的相关性,证明BP_SHPF模型效率排序有效。根据第3节中BP_SHPF模型与传统DEA模型实验结果计算决策单元效率并按降序排列,记为序列X,Y。令Pi为序列X中Xi的秩,Qi为序列Y中Yi的秩,使用参数Bi=Pi-Qi表示两者排序的一致性,则Spearman相关系数可以计算如下:

Spearson相关系数计算结果如表5所示,可发现单产单投BP_SHPF模型与DEA模型相关性系数均大于0.8,多产多投BP_SHPF模型与DEA模型相关性系数均大于0.5,认为两者存在相关性,BP_SHPF模型效率排序可靠。

表5 Spearman相关系数

3 107家农村商业银行生产效率分析

本节将BP_SHPF模型应用于中国农村商业银行效率分析与排序,共收集135家农村商业银行2010年至2018年数据,数据来源为国泰安金融数据库CSMAR及银行机构按规定披露的财务报表。由于农村商业银行公司治理能力弱,部分银行年度报表数据存在缺失现象,对数据进行整理后共获得2014年至2018年107家农村商业银行数据用于模型实证分析,按地区对其进行分类,其中东部地区64家,中部地区36家,西部地区7家,资产负债情况如表6所示。依据谢建辉等[10]实验数据选择,本文选用营业支出、管理费用支出作为投入变量,利息收入和其他收入为产出变量,分别通过BP_SHPF模型和DEA模型计算得出2018年各地区农商行效率均值及标准差如表6所示。实验结果表明,BP_SHPF模型和DEA模型计算的效率均值大小排序一致,均为东部地区农商行效率均值大于西部地区农商行效率均值大于中部地区农商行效率均值。但DEA模型得出的各地区间农商行效率均值差距不明显,东、中地区农商行效率均值差和东、西地区农商行效率均值差分别为0.0365和0.0046,BP_SHPF模型计算东、中地区农商行效率均值差和东、西地区效率农商行均值差分别为0.1818和0.0512,更好的体现了各地区农商行间效率差距。通过实验得出的效率标准差可以发现,经BP_SHPF模型处理后,同一地区决策单元效率值的标准差大于DEA模型,这表明同一地区的农商行效率值更加分散,更好的体现了农商行之间的效率差距。

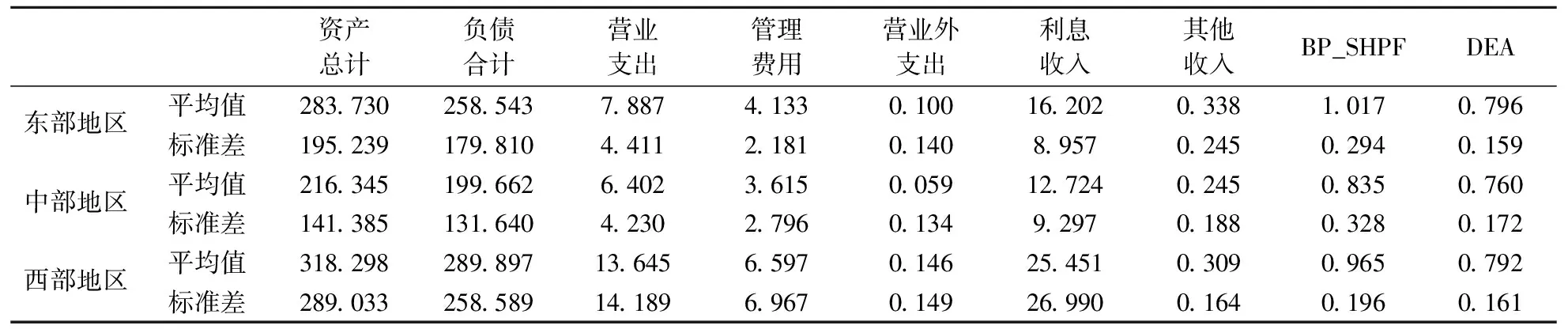
表6 东、中、西部地区银行机构投入、产出及效率均值

图8表示了2014年至2018年期间东、中、西部地区农商行效率变化情况。总体上,2014年至2018年期间东部地区农商行效率均值最优。各地区农商行效率均值呈现先上升再下降后趋于平稳状态,其中,东、西部地区农商行效率均值于2015年达到峰值,中部地区农商行效率均值于2017年达到峰值。值得注意的是2014年至2015年西部地区农商行效率均值明显提升,2016年至2017年中部地区农商行效率均值呈现明显上升,但2018年出现急速回落。

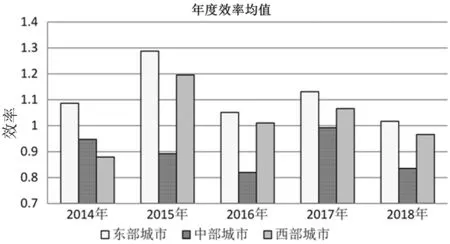
图8 东、中、西部地区年度效率均值

4 结论

在DEA模型的基础上,本文假设贴近生产前沿面的无效决策单元一定概率有效,通过对生产前沿面的后置校正,改善特异数据对生产前沿面的影响,并通过Monte Carlo模拟实验验证模型在单产单投及多产多投生产集合上的效率评估,并证明模型能有效校正DEA模型误差,使用Spearman相关系数分析BP_SHPF模型估算效率与传统DEA模型估算效率的相关性,证明其效率值及效率排名有效。同时,对107家中国农村商业银行效率进行评估,体现BP_SHPF模型具有可用性和实用性。

BP_SHPF模型是一种效率评估方法,其中所使用的BP神经网络主要用于生产前沿面重置,在使用过程中可以尝试用其他机器学习算法进行替代,进一步将模型扩展为DEA模型与机器学习算法结合的集成模型。在实验过程中发现,如数据存在指标为负或数据缺失等数据问题时,则无法使用BP_SHPF模型,如何对不完全数据进行效率分析将是进一步的研究方向。