基于数据驱动的鲁棒最小成本共识模型
2023-11-06韩烨帆屈绍建
韩烨帆, 纪 颖, 屈绍建
(1.上海大学 管理学院,上海 200444; 2.南京信息工程大学 管理工程学院,江苏 南京 210044)
0 引言
共识决策保证了群体决策(GDM)的有效性,广泛存在于我们的日常生活。通过沟通和多轮反馈并调整,最终得到所有DMs都接受的共识意见[1-3],其中修改意见以达成共识的成本最好尽可能低。考虑成本函数是线性函数,最小成本共识(MCC)的概念被提出[4]。DONG等[5]建立了语言环境中GDM的MCC模型。为了说明了上述两类模型的关系,ZHANG等[6]将聚合函数纳入到MCC模型。ZHANG等[7]总结了近十年MCC模型的研究范式并指出未来的研究方向。此外,还有很多MCC模型被提出[8,9]。
个体偏好信息的聚合直接影响综合指标的质量和可靠性,决策者权重必须以适当的方式确定。事实上,即使聚合算子的权重只有微小的变动也可能导致不合理的方案被选择,诱发一定的经济和社会损失。因此,建立一种有效处理聚合过程中权重的不确定性的方法非常必要。
当历史数据可以获得时,从历史数据中确定聚合权重更有利于产生决策者满意的解决方案。但由于社会环境的复杂性和多变性,DMs并不能够解释所有因素。本文旨在利用权重的历史数据,建立基于数据驱动鲁棒优化方法的MCC模型,它可以充分考虑聚合过程中不确定性的历史信息,从而解决不确定性带来的影响。
区间值理论[8]、随机规划(SP)[10]和鲁棒优化(RO)[11]都能有效处理不确定性。因为无需事先定义不确定参数的分布且易于处理,RO受到密切关注并被广泛应用于各个领域[12,13]。但这些经典RO方法都是依据经验得出不确定集合,使得结果过于保守。通过充分利用历史数据信息,数据驱动鲁棒优化方法[14,15]合理地平衡了保守性和经济性。事实上,不确定集合都是基于不确定性的观测数据的[16],其概率密度函数(PDF)可以从历史数据中获得。同时我们可以掌握一定的准确性,如考虑90%的不确定情景并舍弃边界外的极值情况,更符合实际的GDM问题。
本文结合置信水平刻画不确定聚合权重的波动情况,建立了两类柔性不确定集合[17]。作为经典RO方法的拓展,基于数据驱动RO的MCC模型的鲁棒等价式可以利用对偶理论获得,且易于处理。
1 预备知识
1.1 最小成本共识模型
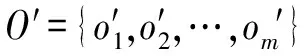

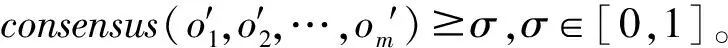



1.2 鲁棒优化及其对等式
考虑一般的线性规划问题:
(1)
其中A∈Rn×m,b∈Rn表示受不确定参数影响的系数矩阵和向量。
定义2(鲁棒可行解) 如果向量x∈Rm满足不确定性集合约束的所有变形,则它是不确定问题(1)的鲁棒可行解。

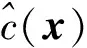
由于不确定LP问题的鲁棒等价式是一个半无限规划问题,增加了求解难度。因此,将这个问题转化为具有多项式可解性的凸优化问题似乎是一个不错的选择。根据不同结构的不确定集合,我们可以得到不同形式的优化问题。最常使用的不确定集有:盒子集,椭球集,多面体集。
2 基于不确定聚合权重的数据驱动鲁棒成本共识模型
由于DMs的教育程度、社会背景等不同,他们在决策过程中所表现出来的重要程度也不同。但在真实的决策环境下,很难准确获得每个DM的权重。因此,我们考虑DMs的权重不确定且在一定范围内波动。模型(M2)的鲁棒对等模型为:

2.1 置信水平约束下的不确定聚合权重

(2)
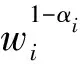
2.2 不确定权重的柔性盒子不确定集合
定义4(柔性盒子不确定集合Ⅰ) 柔性盒子不确定集合基于不确定数据的无穷范数(l∞)定义,它的数学形式如下:

={ξ|‖ξ‖∞≤Φ,Φ=max{qi},∀i∈J}
(3)
其中J表示造成权重不确定的所有系数的集合。当Φ=1,即|qi|≤1时,盒子不确定集合为区间不确定集合。
引理1模型(M3)关于不确定性的约束在经典盒子不确定集下的鲁棒等价式为
(4)
(5)
(6)
(7)

(8)
定义5(柔性盒子不确定集合Ⅱ) 柔性盒子不确定集合的另一种形式为:
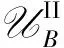
(9)

(10)
2.3 不确定权重的柔性椭球不确定集合
定义6(柔性椭球不确定集合Ⅰ) 柔性椭球不确定集合基于不确定数据的2范数(l2)定义,它的数学形式如下:

(11)


(12)
定义7(柔性椭球不确定集合Ⅱ) 柔性椭球不确定集合的另一种形式为:

(13)

(14)
2.4 不确定权重的柔性多面体不确定集合
定义8(柔性多面体不确定集合Ⅰ) 柔性椭球不确定集合基于不确定数据的1范数(l1)定义,它的数学形式如下:

(15)

(16)
定义9(柔性多面体不确定集合Ⅱ) 柔性多面体不确定集合的另一种形式为:

(17)

(18)
式(5)(6)(7)在六种柔性不确定集合下的鲁棒等价式可用同样的方法得到,为了文章的简洁,这里不再赘述。
通过将上述六种柔性不确定集合得到的相应的鲁棒对等式代入模型(M3),得到六个不同的鲁棒共识模型,分别记为(M4)(M5)(M6)(M7) (M8)(M9)。
3 在碳配额分配管理中的应用
3.1 研究背景
两会期间,“碳中和、碳达峰”备受关注,如何配置市场资源和环境资源是重中之重。通过谈判与协商,政府与所有企业就碳配额达成共识。综合社会效益和经济效益,政府希望以最小的成本帮助企业确定碳配额,这个过程本质上构成MCC问题,政府代表主持人,企业代表DMs。由于企业的地理位置、经济发展等方面存在较大差异,政府在聚合信息的过程中为各企业分配不同且不确定的权重,为气候治理带来很大的风险,有效处理聚合过程中的不确定性尤为重要。
3.2 数值结果和灵敏度分析
本文所有模型均采用Gurobi 9.1.1求解,所有实验都在一台16GB的内存和1.80GHz的4核CPU的PC上进行。
3.2.1 数值结果
假设位于同一省份不同地区的五个污染企业表示为ei,i=1,…,5,它们提出的原始碳配额需求分别为O={0.59,0.36,0.64,0.25,0.42}(单位:10,000吨/年)。为促进最优资源分配,政府愿意支付给他们的单位调整成本为C={6,3,4,1,2}(单位:10,000元/吨)。结合各企业的排放效率和能源利用情况,假设在聚合过程中政府分配给这五个企业的权重分别为w={0.375,0.25,0.1875,0.125,0.0625}。碳配额的标准oc由五个企业期望的加权确定。
为了避免模型的解过于保守,我们考虑基于核的估计方法来获得不确定权重的PDF。假设Wk,k=1,2,…,n是来自总体wi的观测值,核的核密度估计定义为


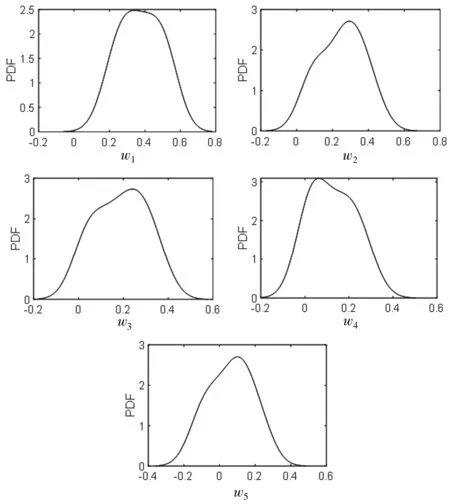
图1 w1-w5的核密度估计曲线
在考虑同比例的不确定情景时,柔性集合Ⅰ比柔性集合Ⅱ的MC小,且不同形状的不确定集对模型结果的影响不同。多面体集最大,椭球集次之,盒子集最小。若政府追求低成本,选择柔性盒子不确定集合Ⅰ,但分配的碳配额资源较多,需要政府均衡好成本和资源。
3.2.2 柔性不确定集合Ⅰ和柔性不确定集合Ⅱ之间基于置信水平的比较
实验1所有不确定性具有相同的置信水平
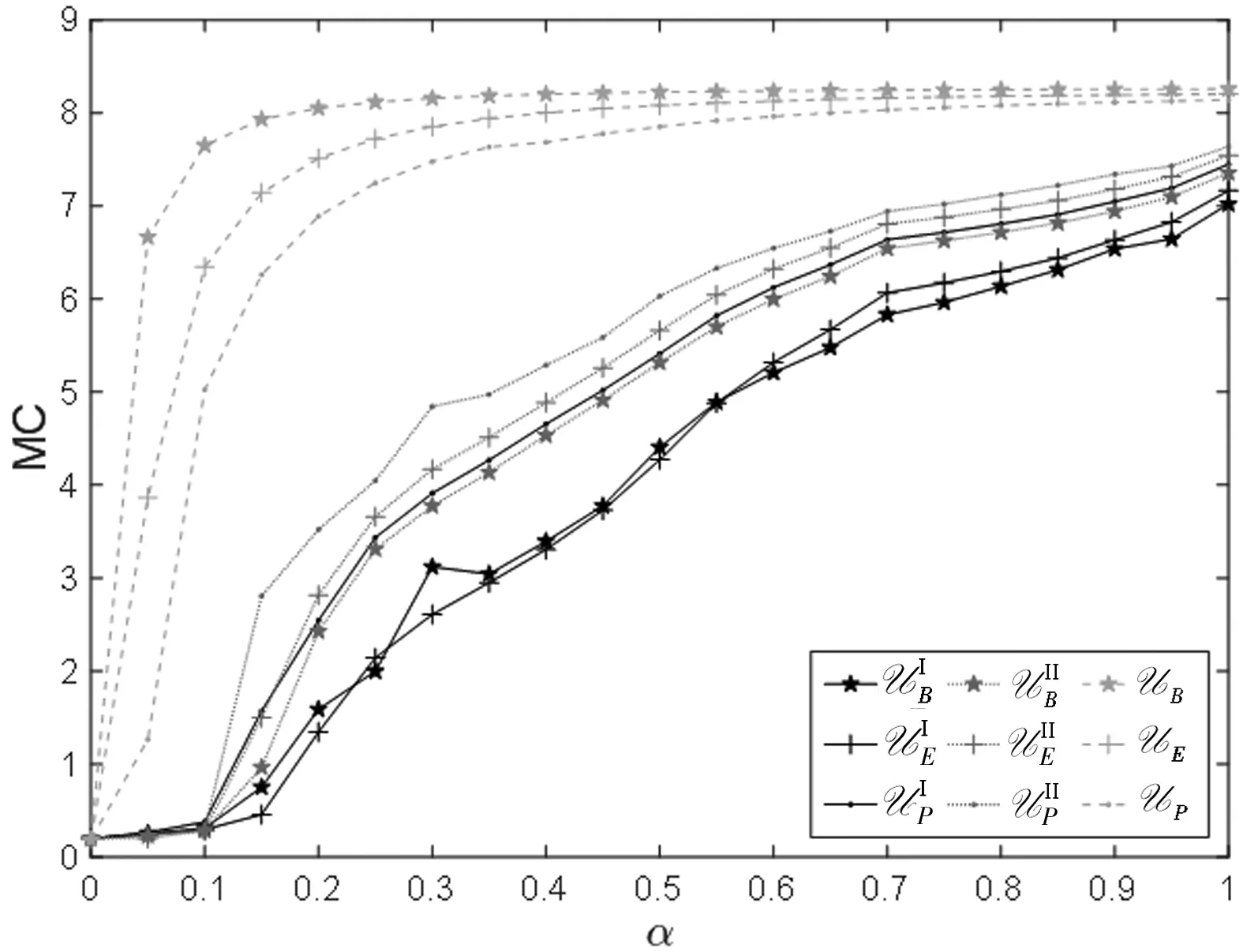
图2 不同置信水平下的MC
随着置信水平的增加,(M4)-(M9)的MC都有不同程度的增加(图2)。为了更有效的达成共识,政府会付出更多成本规避不确定性带来的风险。就集合形状而言,椭球集诱导的MC始终最大,因此柔性椭球集诱导的模型具有更强的保守性。就集合类别而言,相同形状的集合下,柔性集合Ⅱ诱导的MC始终比柔性集合Ⅰ大,即柔性集合Ⅱ的保守性更强。这是因为柔性集合Ⅱ独立考虑了各个不确定性的影响,消除了不确定性之间的耦合情景带来的影响。
实验2不同不确定性具有不同的置信水平
如图3所示,假设每次只改变一个不确定性的波动范围,其他的不确定性保持置信水平为85%。柔性集合诱导的MC始终随置信水平的增增加而增加。其中(d)中的曲线比其他四个更平稳,说明不确定权重w4对于模型的影响最小。w2次之,w1,w3,w5则表现出较大的波动。此外,五个不确定权重在柔性盒子集Ⅰ中诱导的MC在中等置信水平区间上均表现出下降的趋势。此时鲁棒模型的保守性降低,鲁棒性增强。如果政府想要更高效的达成共识,那么可以尝试使用柔性盒子不确定集Ⅰ限制不确定性的边界。但是值得注意得是高回报意味着高风险,这种选择也可能得到不满意的结果。通过计算和预测MC的波动情况,可以帮助政府更好地分配碳配额,并提前制定合理的碳排放交易政策。
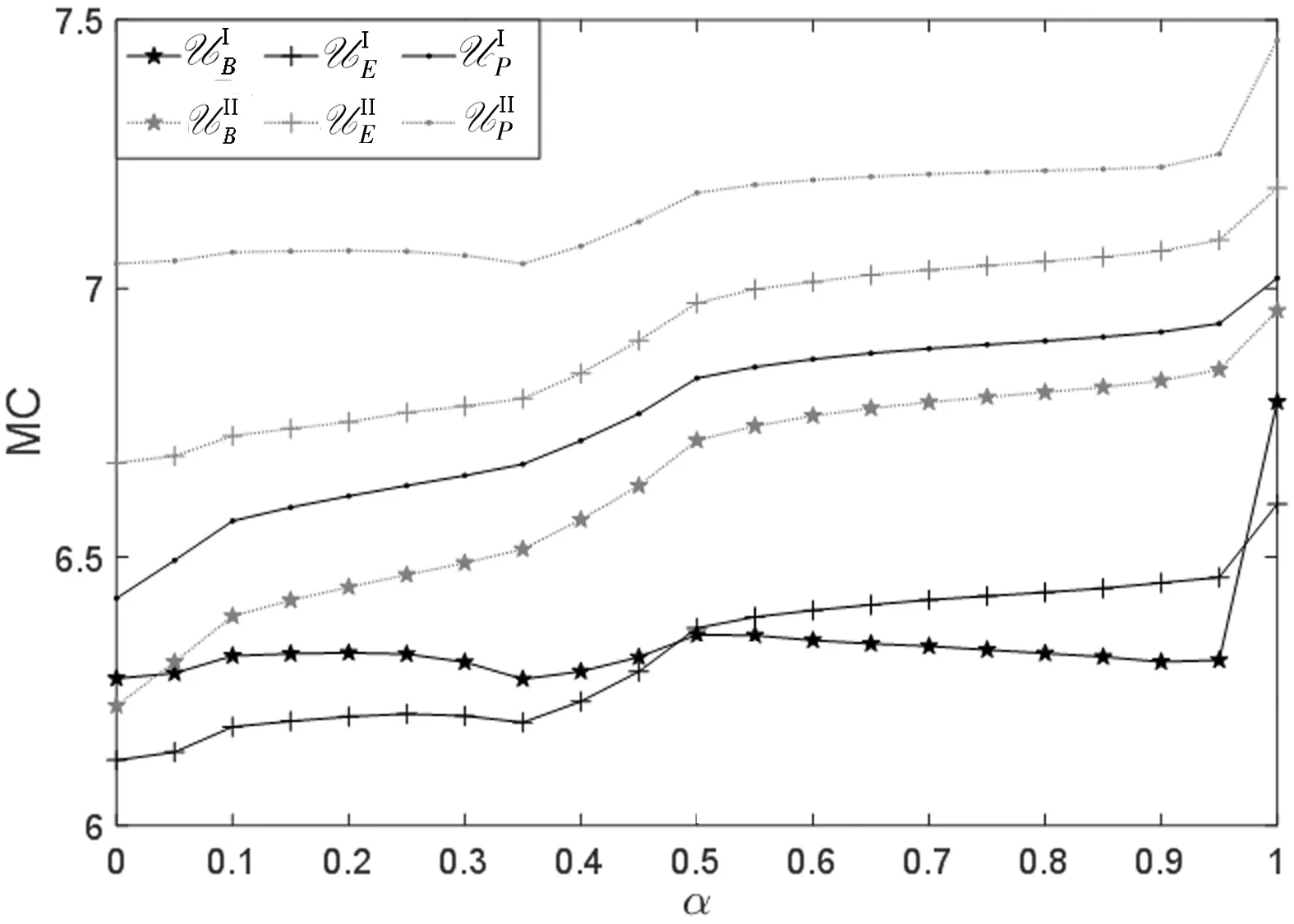
(a)
3.2.3 经典不确定集合和柔性不确定集合的比较

当可调参数增大时,经典集合的MC快速增加,且比柔性集合的MC的增速更快(图2)。在建议的可调参数范围内,当可调参数达到其上界时,经典集合的MC比柔性集合更大。这意味着经典集合诱导的模型比灵活集合诱导的模型的保守性更强。政府可以根据对风险的偏好程度选择合适的不确定集合以制定决策。
4 结论
本文基于数据驱动的鲁棒优化方法处理GDM中的不确定聚合权重。具体贡献总结如下:
(1)基于权重的历史观测数据,考虑聚合权重的不确定情景的不同比例,改变置信水平,可以得到不确定性的界。
(2)利用具有置信水平的不确定权重建立了两类柔性不确定集合,它们可以避免预定义的可调参数造成的保守性。
(3)置信水平越高,考虑的不确定情景越多,鲁棒模型的保守性越强。与经典鲁棒优化方法对比,考虑数据驱动的柔性鲁棒模型具有更少的保守性。
由于大规模的GDM很难达成共识,考虑将所提出的鲁棒共识模型推广到大规模GDM中是很有研究意义的。
