螺旋推进器叶型数值模拟研究①
2023-11-05朱银锋方继根崔清源赵宝剑何友军
周 军, 朱银锋, 方继根, 崔清源, 赵宝剑, 何友军
(安徽建筑大学机械与电气工程学院,安徽 合肥 230601)
0 引 言
关于螺旋推进器的研究,在20世纪六七十年代国外的研究人员针对螺旋式驱动车辆的通过性做了大量的研究,但是翻阅这一时期的文献,很少有将螺旋式驱动结构应用到更小的管道机器人方面的运动特性研究,然而现如今管道在工业和日常生活中,都起着不可替代的作用。特别是近几年,随着城市化不断加深,城市内的排水管道长期处于各种各样的复杂环境里,随着时间的增长,管道的腐蚀、裂纹以及污物沉淀等问题不可避免。针对排水管道内的复杂环境,采用螺旋推进器提供动力的两栖螺旋管道机器人整体体积小,两侧螺旋推进器浮力大,滚筒旋转推动力强,特别适合在环境复杂的管道内行驶[1]。但全地形两栖螺旋管道机器人的螺旋推进器是一种非常规螺旋推进装置,通过求解N-S方程和相关方程组模拟螺旋推进器工作时周边的流场环境非常困难[2]。
通过理论计算得出螺旋推进器在地面移动最佳螺升角度区间,再对此区间内不同叶型螺旋推进器的敞水性能进行数值模拟仿真,并通过研究结果为全地形两栖螺旋管道机器人的设计与优化提供参考方向。
1 螺旋推进器运动学模型建立与计算
1.1 运动学模型建立
螺旋推进器的理想三维运动模型如图1所示[3],为了更好地模拟其运动方式,首先需要建立整体坐标系o-xyz,其次针对螺旋推进器建立运动坐标系o-xyz。螺旋叶片之间螺距h和叶片螺旋升角λm满足关系式(1),(2):
h=π(r+r1)tanλm
(1)
r=r1+r2
(2)
式(1),(2)中:r1为螺旋推进器半径;r2为螺旋叶片的高度。
螺旋推进器的有效长度b与螺距h有关:
b=N·h
(3)
式(3)中:N为螺旋线环绕圈数。
1.2 地面运动计算
假设螺旋推进器在地面运动时,减速电机在螺旋筒内部带动螺旋推进器旋转,由于螺旋叶片存在一定的倾角,所以地面会受到螺旋叶片向后的挤压力,从而推动螺旋推进器在地面向前运动,等同于土壤沿着叶片斜面(以螺旋面的螺升角λm作为斜度角的斜面)的轴向向后运动。如图2所示,在运动过程中土壤会对螺旋推进器会产生轴向挤压应力P,假定螺旋叶片的工作表面与土壤之间的摩擦角为Φ,将螺旋叶片工作表面单位面积对土壤的支撑反力设为N,螺旋叶片与土壤的轴向剪切应力设为τ,由于螺旋推进器贴近于地面轴向滑动,土壤在推进器滑动过程中所受到的重力是极小的,可以忽略不计。通过物体的受力平衡基本原理,螺旋推进器施加于土壤的轴向剪切力应力τ如图2。
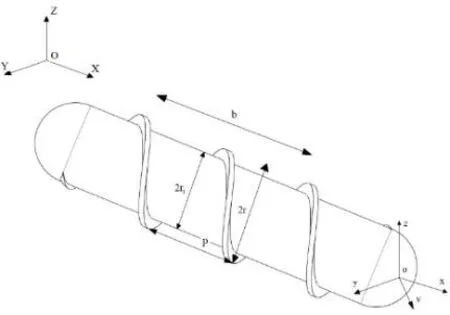
图1 螺旋推进器运动模型
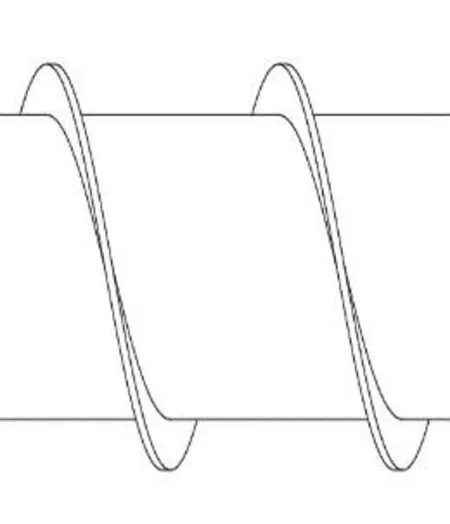
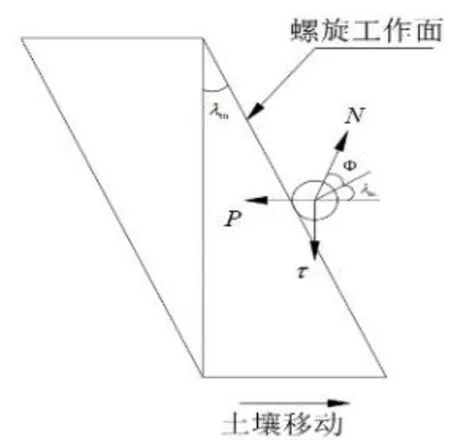
图2 土壤向后移动受力示意图
N·cosλm=P+f·N·sinλm
(4)
N·sinλm+f·N·cosλm=T
(5)
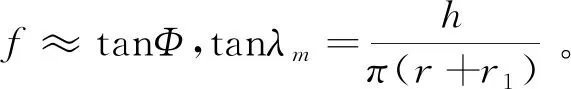
联立式(4)和式(5)可以得出:
τ=P·tan (λm+Φ)
(6)
式(6)中,当螺旋推进器的螺旋升角λm等参数确定后,螺旋推进器施加于土壤的轴向剪切应力τ只与摩擦角Φ相关。欲使螺旋推进器向前运动,即使土壤向后轴向运动,必须有0<λm<90°,将τ对Φ求取导函数得到[4]:
(7)
式(7)中,τ是Φ的递增函数。为增大螺旋推进器的工作效率,即降低螺旋推进器在贴近地面旋转过程中的阻力矩大小,则必须要减小螺旋叶片工作面与土壤之间的轴向剪切力τ,可以通过减小土壤与螺旋工作面之间的摩擦角Φ,增大螺旋推进器的工作效率。
土壤与螺旋推进器螺旋工作面之间的摩擦角度Φ与多种因素有关,其中包括螺旋推进器自身的转速,螺旋叶片的起始螺升角度,螺旋推进器的整体结构形式以及螺旋推进器的表面材质。通常情况下平整光滑的工作表面可以最大限度地降低与土壤之间的摩擦角度Φ,可以采用铝合金材质制造螺旋推进器,铝合金表面与土壤之间的最小摩擦角近似为Φ=23°~33°[4]。
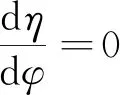
sin2(λm+φ)-sin2λm=0
(8)
由于:0<λm<90°,0<Φ<90°,那么,0<λm+Φ<180°,由此可得:
sin2(λm+φ)=sin2λm=sin (180°-2λm)
即2(λm+φ)=180°-2λm,从而得到λm=45°-Φ/2。
将土壤与铝合金螺旋工作面之间的最小摩擦角Φ=23°~33°带入后得到λm=28°30,~33°30,。
螺旋推进器要在地面获得较高的推进效率,在不更改其他工作参数的情况下,叶片的起始螺旋升角应在λm=28°30,~33°30,这个区间内。
2 流场分析的基本控制方程
通过地面推导理论计算得到螺旋推进器地面运动最佳螺旋升角范围,再对螺旋推进器在敞水中运动状态进行分析,螺旋推进器在敞水中旋转运动,此过程中流体在螺旋推进器周围的流动特性可以通过基本控制方程来描述。
2.1 连续性方程
(9)
式(9)中:ux,uy,uz分别为坐标轴上3个方向的速度分量,m/s;t为时间,s;ρ为密度,kg/m3。
引入哈密顿微分算子:
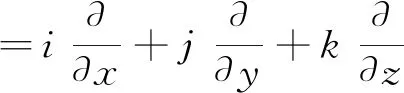
(10)
则式(9)可表示为
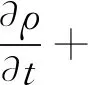
2.2 动量方程
通过动量守恒定律即在满足牛顿第二定律的情况下,螺旋推进器周围的流体微元,其动量对时间的变化率等于外界作用在微元体积上的各种力之和。由此,推导出螺旋推进器在x轴,y轴和z轴三个方向的动量方程分别为:
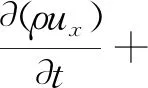
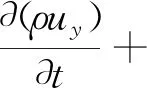
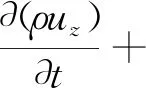
这里采用k-ε湍流模型与上述方程组构成封闭的方程组。
3 螺旋推进器模型建立
3.1 实体模型建立
研究选用经典的两栖螺旋推进车(Marsh Screw Amphibian,MAS)为参考对象[5],按照国内排水管道尺寸,设计全地形两栖螺旋管道机器人,其中螺旋推进器各项数据参数如表l所示。

表1 螺旋推进器结构参数
在满足表1螺旋滚筒结构参数情况下,为得到在地面最佳螺旋升角范围内螺升角改变对螺旋推进器在敞水中运动参数的影响,设计28°30,,29°30,,30°30,,31°30,,32°30,,33°30,六组不同叶型螺旋推进器模型进行流体运动学仿真,建好的螺旋推进器三维模型如图3。

图3 螺旋推进器三维模型
3.2 计算区域建立
出于计算考虑,只对螺旋推进器其中一个螺旋筒进行仿真分析,以螺旋筒为中心,建立2000mm*3000mm的圆柱体外流场静止域以及230mm*800mm的圆柱形内流场旋转域,这样放便划分网格以及设定流体域特性,可以提高计算结果的准确度[6]。
3.3 网格划分
网格划分质量的好坏直接影响到螺旋推进器解析的敛散性和结果的准确性。在网格划分中采用四面体网格,将内流场旋转域内螺旋推进器外表面网格单元尺寸设置为5mm,内流场旋转域整体网格单元尺寸设为10mm,降低外流场静止域网格密度[7],网格单元尺寸设为100mm,这样既可以得到较为精确地结果,也可以降低计算机解析过程中的计算量,并且可以提高计算效率[2]。如图4所示。

图4 螺旋推进器网格划分
3.4 边界条件确定
将进口的边界条件定义为inlet,并设置为速度入口,由于是在静水中模拟,所以进口速度设置为0;将出口边界条件定义为outlet[8],由于出口速度与压力未知,所以选择默认;螺旋筒的表面设置为移动旋转壁面,相对计算域内流体绕轴角速度为n=0rad/s旋转,近壁区采用增强壁面函数EWF;内流场旋转域内流体设置运动参考系,确定旋转轴原点,绕轴以角速度n=18. 85rad/s旋转。
4 计算结果及分析
4.1 数据分析
通过对六种模型在敞水中进行仿真后得到了这六种螺旋推进器的推力T和最大轴向运动速度vmax随螺旋升角的变化情况,如表3以及图5、图6所示。
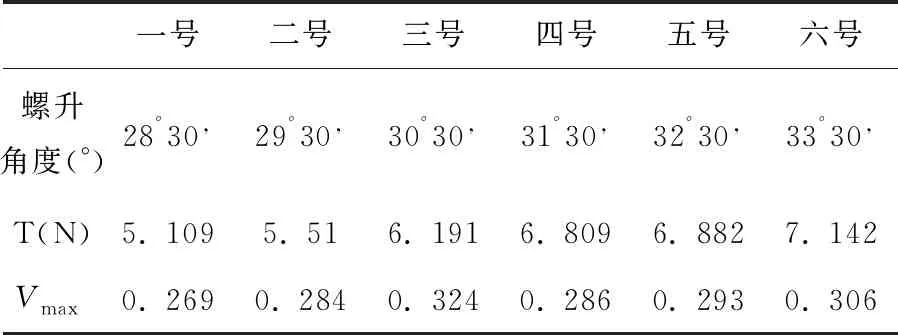
表3 各性能参数随螺升角度的变化表
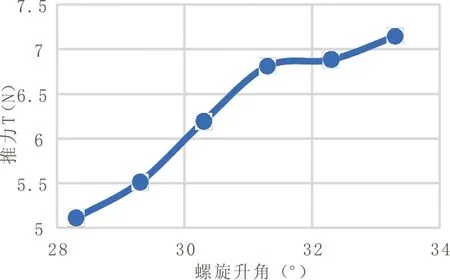
图5 推力随螺旋升角的变化情况
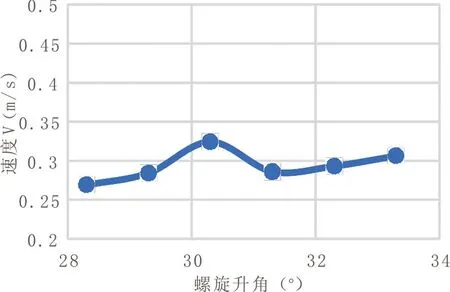
图6 速度随螺旋升角的变化情况
根据得到的物理量(T和Vmax)为螺升角度曲线可知:
(1)在28°30,~33°30,范围内,螺旋推进器在敞水中获得的推力是逐渐递增的,螺旋推进器对周围流场的影响随着螺旋升角的增大逐渐增大;
(2)螺旋升角在28°~33°范围内螺旋推进器速度存在极大值。
4.2 螺旋筒表面流体轴向速度分布(Z方向)
由于螺旋推进器叶片的连续性,不同起始螺升角度的螺旋推进器对周边流体动量的转换效率不同,通过改变叶片起始螺升角度从而改变流体经螺旋推进器时的运动情况,进而改变轴向速度增量[7]。
经仿真获得六种螺旋推进器在流场中流速分布情况如图7所示。在螺旋推进器表面上的不同位置,流速的差异比较明显。其中,螺旋推进器沿Z轴这个方向螺旋推进器前端流体流动速度较小,流体速度接近于0。流速主要集中在螺旋推进器末端,最大流速可达1. 88m/s。
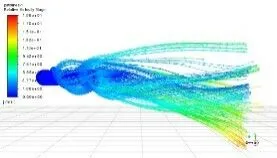
(a)一号
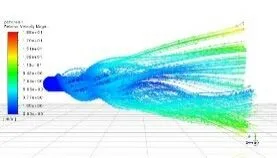
(b)二号

(c)三号
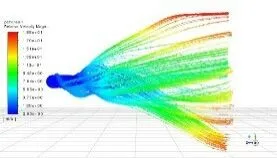
(d)四号
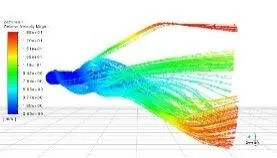
(e)五号
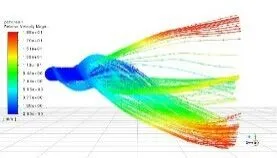
(f)六号
螺旋升角变化对流体流速影响较为明显,随着螺旋升角在最佳范围内逐渐增大,流体被逐渐压缩于螺旋推进器末端,应力集中,所以流体对螺旋推进器推力逐渐增大。
4.3 螺旋筒轴向速度分析(Z方向)
通过比对不同型号螺旋推进器轴向速度平面云图图8可以发现,螺旋推进器在在敞水中,速度随螺旋升角增大总体上是逐渐增大的,螺旋推进器螺旋升角在29°~31°范围内速度存在极大值。通过对轴向平面云图观察发现,螺旋推进器螺旋升角为30°30,螺旋推进器对周围流体环境影响相较于29°30,和29°30,更大。

(a)一号

(b)二号

(c)三号

(d)四号

(e)五号

(f)六号
4.4 表面压力分析
通过对图9-图11进行观察可以发现(均为敞水):
(1)沿Z轴正方向螺旋叶面起始受压较小,随着流体经过螺旋叶片螺旋导流,螺旋叶面受压逐渐增大;(2)沿Z轴负方向螺旋叶背起始受压较大,流体经过螺旋叶片导流至末端,螺旋叶背受压逐渐减小;(3)三号螺旋推进器叶面最大受压达到370Pa,充分说明三号螺旋推进器叶片螺升角度对于流体沿Z轴正方向反作用力利用效率更大;(4)结合螺旋滚筒表面流体轴向速度平面云图,可以证明螺旋推进器在流体中旋转产生的推力是流体与螺旋推进器之间产生作用力与反作用力的结果。


图9 一号叶片压力云图(左测叶面右侧叶背)


图10 三号叶片压力云图(左测叶面右侧叶背)


图11 六号叶片压力云图(左测叶面右侧叶背)
5 结 论
通过开展研究得到了全地形两栖螺旋机器人螺旋推进器的最佳叶型参数:
(1)螺旋推进器叶片螺旋升角在28°30,~33°30,这个范围内时,螺旋推进器获得最佳的地面推进性能。
(2)在螺旋推进器地面最佳角度范围28°30,~33°30,内,随着螺升角增大,螺旋推进器在敞水中获得的正向推进力逐渐增大。
(3)在敞水中螺旋推进器螺旋升角在29°~31°范围内速度存在极大值,螺旋推进器螺旋升角为30°30,时螺旋推进器对周围流体环境影响相较于28°30,和29°30,更大,螺旋升角在29°~31°范围内对流体的反向作用力沿Z轴正方向利用效果最高。
(4)全地形两栖螺旋管道机器人在地面和流体中都能获得较高的行驶速度以及最佳机械效率,螺旋推进器叶片螺旋升角应在29°~31°范围内。
