基于优化K均值聚类的高校网络异常流量分析方法研究①

商鸿发

(浙江旅游职业学院,浙江 杭州 312231)

0 引 言

经过多年的建设与发展,我国互联网正逐渐转变为一种大规模、高容量的创新型技术,并渗透到人们生活的各个角落[1-2]。除了网络对人民生活产生的影响外,“网络+教育”的发展也是当前我国信息化教育的重点建设部分。高校作为培养大学生的主要阵地,其中互联网的建设与发展受到了社会大众的广泛关注,其中校园网络是我国大学校园网络建设的一个重要环节。校园网为我国高校的信息发布以及教师自动化办公提供了重要运行环境,但校园网也存在有功能发挥不充分的现象[3-4]。例如网络建设薄弱,容易受到外来入侵;容量较小,不能同时容纳所有师生登录使用学校网站等问题。鉴于此,研究提出基于优化K均值聚类的高校网络异常流量分析方法,首先利用IRNN对校园网流量展开预测,接着融合到传统K均值聚类算法中,构建一种改进优化K均值聚类算法,期待能够有效地检测校园网异常流量变化,促进高校网络安全建设。

1 基于优化K均值聚类的高校网络异常流量分析方法研究

1.1 基于IRNN的流量预测方法

为了解决传统RNN存在的数据梯度消失依赖问题,有学者提出使用基于时钟驱动的循环神经网络模型(Clock-driven cyclic neural network, CW-RNN)。改进后的RCW-RNN神经网络模型如图1。

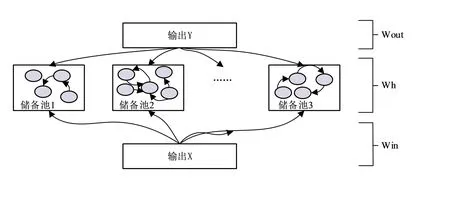
图1 RCW-RNN神经网络结构模型

图1中可以看出,为了提高检测精度、改变激活标准原则以提高预测效率,该模型尤其着重于引入随机权值。研究将RCW-RNN分成了不同的储备池模块,并保留生成的不同机制,为每一个储备池分配同样的时钟周期[6]。如图1所示,在t时刻,改进后的神经网络模型输出表达如式(1)。

(1)

式(1)中,fout表示输出层的激活函数;Wout表示输出层的连接矩阵;yh(t)表示在t时刻的隐藏层输出(是g个隐藏层储备池输出构成的向量)。隐藏层向量输出如式(2)。

(2)

式(2)中,fh表示隐藏层激活函数;Wh表示隐藏层连接矩阵;Win表示输入层连接的矩阵;xin(t)则表示处于t时刻的输出。yh(t′)是不同的储备池对应的前一状态;γ表示前一状态的储备池在当前状态中占据的主要比例,取值区间为[0,1]。由于储备池的周期不同,对应的不同时期状态也不同,因此计算方程也不尽相同,具体方程计算如式(3)。

(3)

式(3)中,利用CW-RNN的指数增长模型(表达为Tg=2g-1),可以在很短的时间内利用少量的储备来实现更大的时间范围跨度。然而在当前网络识别的方法中,通常使用机器学习算法对网络流量数据集进行数据的采集与整理。因此研究引入K均值聚类算法对数据进行再处理。

1.2 优化的K均值聚类算法设计

原始的K均值(K-means)聚类算法,主要利用数据间距离与数据指标间的相关系数表示数据的相似性。在实际计算过程中,当收敛速度与最小误差平方值最优时,算法结束运行,接着获得最终分类结果。针对这一问题,研究提出了一种基于不同数据特征分布的初始聚类中心(K均值优化)的方法,以避免产生局部最优解。优化K均值聚类算法实验开展过程中,首先对特征值进行选取。校园网流量作为一种不确定的变量,一般利用信息熵对其进行表示,具体如式(4)。

HX=-∑x∈xp(x)logp(x)

(4)

利用式(4)求得的熵值,将网络流量数据中差距较大的特征数据值作为实验参数。研究选取流量数据集进行有效测试,该数据集包含有总数据500万条,其中进行测试与训练的子集各为50万条。在实际实验过程中,所有数据集都必须经过预处理,保证输入数据之间的差距较小。预处理表达式如式(5)。

(5)

式(5)中,max表示最大数据值;min表示最小数据值,X*表示标准化结果。为了更好地对算法的设计进行说明,研究假设有网络数据集S(S=f1,f2,…,fn),n表示网络数据流个数。在网络数据集S当中,1表示向量的维度,而利用对应网络流量的特征属性数值表示向量中的每个元素。假设数据集合为S={xi|xi∈Rm,i=1,2,3,…,n},n代表一个集合中的所有数据对象总数量;m表示空间数据最终维度值。在优化K均值聚类算法中,数据对象之间的测量与聚类收敛标准如式(6)。

(6)

式(6)中,x,y表示属性向量;Cj={cj1,cj2,…,cjn}T表示聚类中心;k表示初始聚类数量;oj表示簇cj中所有数据点之间的平均值;cj表示分类簇。研究引入流量密度的概念到优化K均值算法中,得到数据集合S中数据对象之间的平均距离,以及集合S中某一数据对象xi的密度,具体计算如式(7)。

(7)

(8)

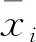
(9)

(10)

式(10)中,din(k)表示簇内距离。当din(k)越小,对应集合S中簇内的数据对象间的相似性越高。为了满足上述假设,研究引入聚类效果判定函数,表达如式(11)。

V(k)=din(k)/bds(k)

(11)

式(11)中,V(k)表示集合的簇间聚类。当集合的簇内距离越小,簇间距离就越大,判别函数的值就越小。当判别函数有最小值时,数据集合S中的数据对象之间的相似性就有最大值,对应不同簇的数据对象之间的差异性也就有最大值。即可以选择合适的k值,使得判别函数V(k)有最小值,进而将此k值作为最佳聚类效果所对应的簇的个数值。将优化后的K均值聚类检测流程绘制如图2。

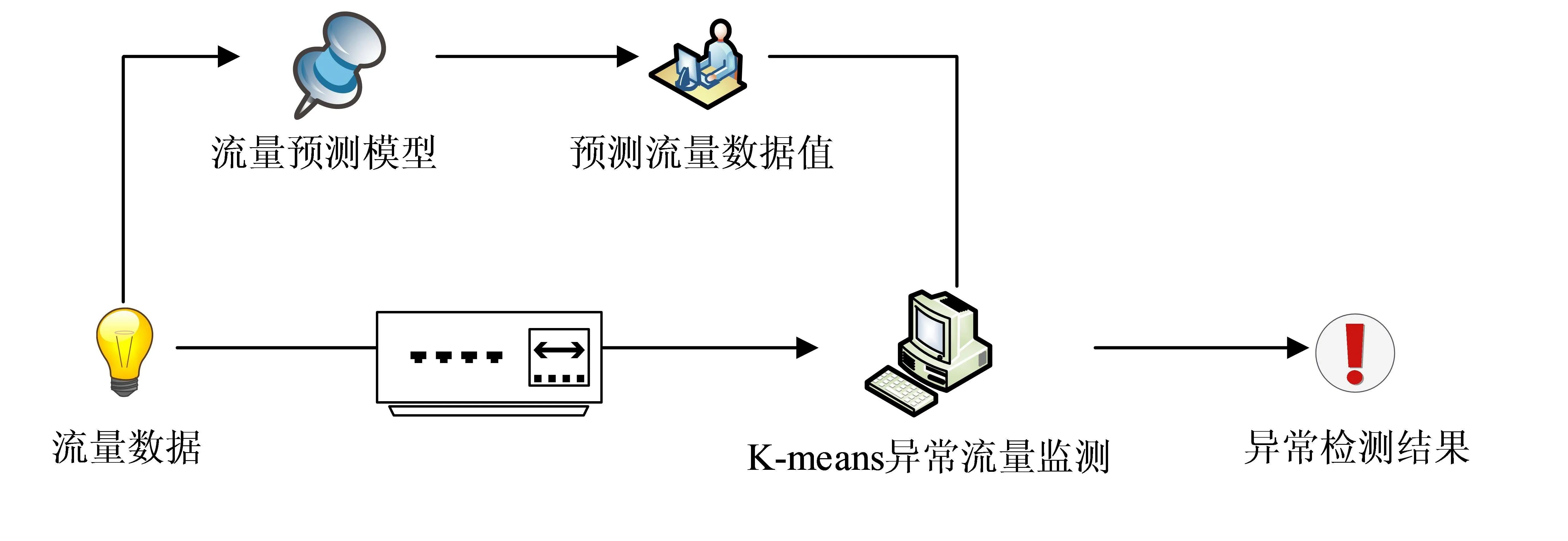
图2 优化后的K均值聚类检测流程

2 高校异常流量分析检测模型的仿真实验

为了验证研究所构建方法能够对高校异常网络流量进行快速且准确的检测识别,研究采用两个不同的公开流量数据集进行流量预测的仿真实验。两个数据集分别为美国主干网络流量数据与11个北美城市的流量数据集,两个数据集涵盖约两个月内每5min采集的汇集流量。所有实验均在相同的设备环境中进行。首先对算法的检测率与误报率两个指标进行性能对比,所得对比结果如图3。

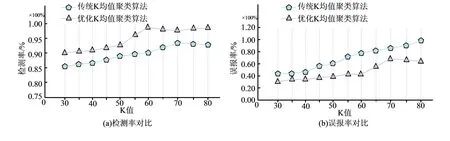
图3 不同算法的检测率与误报率对比

图3(a)与(b)中发现,随着K值的增加,所有算法的检测率与误报率均表现出明显的增长趋势。图3(a)中,研究方法运行下检测率显著高于传统K均值聚类算法。当K=60时,研究算法的检测率开始趋于稳定,此时的检测率为98.21%;当K=70时,传统K均值聚类算法的检测率为93.92%。图3(b)中,研究方法的误报率显著低于传统K均值聚类算法。当K=70时,研究算法的误报率为0.661%;传统聚类算法的误报率为0.812%。对比可知,优化后的研究方法能够同时拥有高检测率与低误报率,且有助于得到全局最优解。

为扩大对流量变化曲线的观察,研究对北美11个城市的流量数据进行收集,选取5.8×103到6.0×103min时间段内的局部预测误差曲线如图4。

由图4可知,在三种方法中,传统的K均值聚类方法对整体的预测误差影响较大,最大误差在5882min附近,此时误差约为2.210×108。而整体RCW-RNN与研究算法较为相似,预测误差整体区间在[0.0～1.500×108]之间波动。其中RCW-RNN在所选时间段内的最大误差出现在5948min附近,对应预测误差值为1.481×108。同时研究算法的最大误差出现在5810min附近,对应预测误差约为1.472×108。对比可知,研究算法的最大误差均小于传统K均值聚类误差与RCW-RNN误差。使用研究方法对网络流量进行较好检测,并且误差率较低。为了更加直观地观察三种方法的差异,研究对不同算法进行网络应用识别准确率与总体识别准确率的对比,具体如 图5。

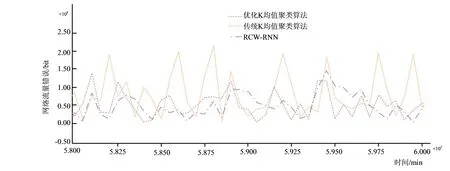
图4 不同算法在北美11个城市的流量

数据集上的部分预测误差结果从图5(a)中可以看出,当研究方法没有选取K值对准确率进行对比时,任意改变网络应用,改进后研究算法的识别准确率仍然显著高于传统聚类算法,这表示研究所构建方法对网络流量分类的影响是积极的,优化的效果能够得到验证。图5(b)中可以发现,被标记的流量数据占比越高(数量越多),相应的K均值算法在准确率和稳定性上都有很大的提高。在15%的标记流量数据占比下,网络流量的识别准确精度显著高于90%,即研究所提出方法可以很好地满足一般高校校园网流量数据变化的识别要求。

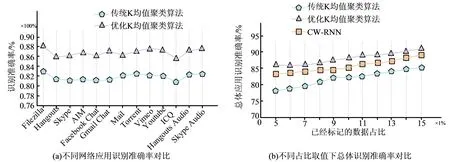
图5 不同算法的识别准确率对比

3 结 语

为了让学校管理人员能够更全面地了解校园网络流量变化,更准确地监测网络信号变化,研究对高校校园网络的监测问题展开了讨论,亟待提升对网络的检测准确率。研究首先引入循环神经网络与传统K均值聚类算法相互结合,对样本数据进行预处理;接着将处理后数据代入K均值聚类算法中,得到有效的结果。结果显示,研究算法在聚类K值为60时,有最大检测率98.21%,而传统K均值聚类算法的检测率较小;在聚类K值为70时,传统算法与研究算法的误报率分别为0.812%,0.661%;部分流量数据集预测结果中,运行时间在5810min附近时,研究算法有最大误差1.472×108,传统K均值聚类算法与RCW-RNN算法的最大误差为2.210×108与1.481×108;当标记数据占比为15%时,网络流量的识别准确率可达到90%以上。以上结果均表示研究所构建优化K均值算法的识别准确率高,稳定性能好,并且具有高检测率与低误报率的优秀性能。但是在将来,网络攻击的技术手段越来越多,为了更好地检测到异常流量的变化,必须进行更多的试验研究,以丰富研究结果。