一种TSDF判别算法的自适应阻抗保护研究①
2023-11-05龚晓龙
龚晓龙, 李 梅
(安徽理工大学电气与信息工程学院,安徽 淮南 232001 )
0 引 言
阻抗保护广泛用于高压输电系统中,其保护Ⅲ段为电力系统中的输电线路提供后备保护,Ⅲ段的保护范围使得其在低频振荡期间更容易误动。针对上述问题,文献[1-8]提出了许多方案。
文献[1-2]针对由于过渡电阻的存在,采用一种自适应阻抗保护方法来提高耐受过渡电阻的能力。文献[3]在分析区外故障时自适应阻抗保护误动的基础上,提出一种自适应阻抗保护的改进方案。文献[4]针对由于超高压送电线路的稳态超越造成的电力系统输电情况变动时电阻误差计算不准确,提出一种超高压送电线路自适应阻抗保护技术。文献[5]针对传统阻抗保护整定繁琐而造成的灵敏度不足,提出一种基于自适应在线整定方法的阻抗保护方案。文献[6-7]提出一种自适应整定算法,解决了因传统算法整定值固定不变而造成的保护误动。文献[8]就用户整定定值前置、自适应整定定值后置、自适应整定原则作了较全面的研究,并提出了各保护定值自整定的方案。回顾文献[1-8]可知,尽管方法可能不同,但许多自适应方法都是应用在电力系统正常运行状态下,并没有考虑电力系统紧急状态,如低频振荡。
使用Matrix Pencil(MP)方法,以解决在阻抗保护Ⅲ段内发生三相故障时的检测和判别问题,MP方法在各个工程领域都有许多应用,用于传感器状态的检测,用于电缆电弧故障定位,用于雷达目标分类,用于电力系统动力学分析,用于信号处理[9-13]。将故障电流信号作为实际输入信号,基于实际信号与重构信号的振幅差值,提出瞬态监督检测函数(Transient Supervisory Detection Function, TSDF),将TSDF用于检测区分三相故障与低频振荡。通过仿真,验证了所提算法的有效性。
1 自适应方案
当被保护线路发生区内故障时,保护元件应当及时动作。当电力系统发生低频振荡时,保护元件应避免误动。为了正确区分三相故障和低频振荡,文中采用了以下两个判别算法:1)使用传统的阻抗区域识别算法来初步判别事件;2)使用所提出的TSDF来最终判别事件。
1.1 使用传统判别算法
在保护安装点处测得的电压、电流可以表示为:
v(t)=Vmsin(ωt)
(1)
i(t)=Imsin(ωt+θ)
(2)
式中:Vm是电压振幅;Im是电流振幅;ω是角频率;θ是电流超前电压的角度。
(3)
正常情况下,保护装置所测得的视在阻抗要远大于其本身所设的整定阻抗。此时,保护装置不会动作。当发生低频振荡时,对于没有安装振荡闭锁(Power Swing Blocking, PSB)元件的保护装置来说,保护装置所测得的视在阻抗可能会小于其本身所设的整定阻抗。此时,保护装置会发生误动;对于已经安装了PSB元件的保护装置来说,若发生低频振荡的同时,线路再发生三相故障,PSB元件可能使保护装置无法跳闸切除故障。为了避免上述两种不正常情况的发生,文中使用MP方法计算得到的TSDF作为第二判别算法。
1.2 使用TSDF判别算法
在判别算法1中,如果正序阻抗ZP小于阻抗保护Ⅲ段的整定阻抗,此时为了确定是否真正存在故障,则还应通过判别算法2来核验。在判别算法2中,通过MP法重构电流信号来提取用于状态分析的有用信息。
在文中,MP法用于估算TSDF的指数g。如下所示:
1)计算重构信号与原始信号之间的差值。
(4)
式中:N为采样点数。
2)将TSDF定义为去除掉最大的绝对误差和最小的绝对误差之后,剩余误差的绝对值之和的平均值。
(5)
3)当发生三相故障时,至少可以在电流信号三相中的一相中,观察到显著衰减的直流分量[14]。将TSDF的指数g定义为:
g=max(TSDFa,TSDFb,TSDFc)
(6)
1.3 自适应阈值的计算
电力系统是一个高度复杂的系统,基于固定阈值的保护算法可能不适用于所有的操作场景,文中所提出的算法中应用了自适应阈值。
中国教师:您曾说过,一个没有阅读的学校永远不可能有真正的教育,您认为,阅读与学校教育的关系是怎样的?目前,学生中普遍存在阅读浅层化、低俗化现象,您认为解决的关键是什么?
1)令矩阵H定义为,从矩阵D中去除掉最大的绝对误差和最小的绝对误差之后,剩余误差所构成的矩阵。
H=[h1,h2,h3,…,hN-2]T
(7)
2)在一个完整的采样周期中,从H提取出最小值hmin和最大值hmax。
hmin=min|hi|,(i=0,1,2,…,N-2)
(8)
hmax=max|hi|,(i=0,1,2,…,N-2)
(9)
3)将阈值gth定义为最小值hmin和最大值hmax的平均值:
(10)
如果g>gth,则说明发生了三相故障。
1.4 算法流程图
集成算法的流程图如图1所示。使用三相电压和三相电流计算正序阻抗。如果计算出来的阻抗小于阻抗保护Ⅲ段的整定阻抗,则使用判别算法2来核验判断。
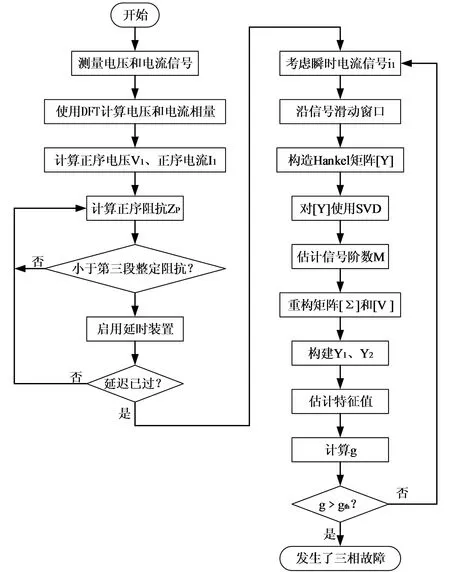
图1 算法流程图
2 仿真验证
2.1 仿真系统
可以将PSCAD与MATLAB进行联合使用。在PSCAD/EMTDC软件中,搭建的仿真模型示意图如图2所示。该模型将用于验证所提集成算法的性能。
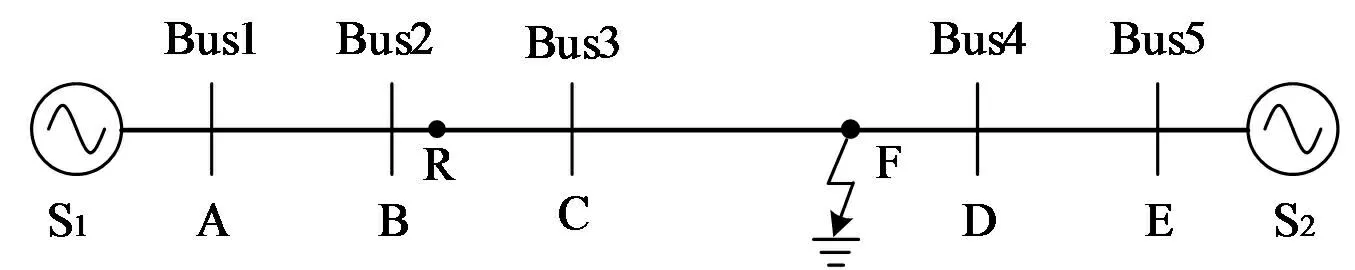
图2 双端电源系统示意图
图2所示系统为220 kV系统,电源S1电压为242 kV,电源S2电压为220 kV,电源S2滞后电源S110°,忽略电源内阻抗。线路AB长度为100 km,线路BC长度为100 km,线路CD长度为100 km,线路DE长度为280 km。R点为保护装置安装点,F点为故障点。架空线路线型为LGJQ-400/35,线路参数如表1所示。为模拟电力系统振荡情况,将电压源S2的频率设为49.8 Hz,电压源S1的频率设为50.2 Hz。
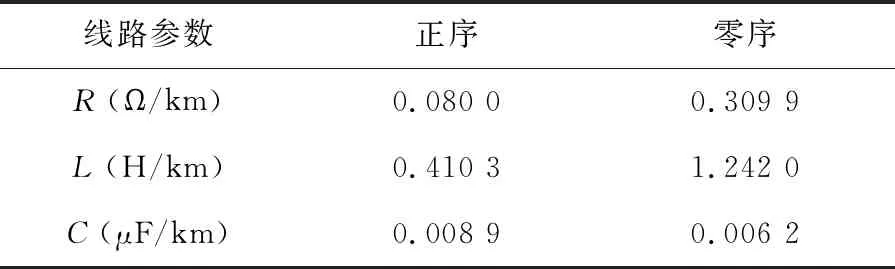
表1 线路电气参数
仿真时,系统的采样频率为1 kHz,工作频率为50 Hz。在时域输入信号上,MP方法通过滑动窗口并可视化相对于窗口信号时间的参数来实现参数提取。分析时,滑动窗口的长度为20 ms。
2.2 系统单纯振荡情况仿真
在稳定振荡期间,基于传统的阻抗保护Ⅲ段设置,如果保护装置R没有安装PSB元件,则R会认为此时发生了故障,并发出动作指令。系统单纯振荡无故障情况的仿真结果如图3所示。

(a) 计算结果图
(b) 保护动作图
由图3(a)可以看出,当系统仅发生振荡而无故障时,g值一直位于阈值gth以下,保护装置不动作。集成算法能有效防止保护装置在振荡时误动。
2.3 系统单纯故障情况仿真
三相故障F发生在175 km处,即F点距R点175 km,故障发生时刻为2.5 s,故障持续时间为0.5 s。系统单纯故障无振荡情况的仿真结果如图4所示。
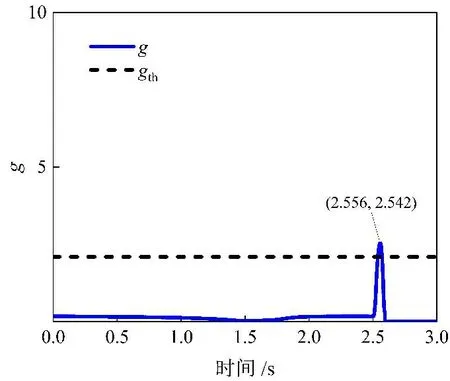
(a) 计算结果图

(b) 保护动作图
由图4(a)可以看出,当系统仅发生故障而无振荡时,g值在故障发生后位于阈值gth以上,保护装置动作。集成算法在2.556 s检测出故障,并进行保护。
2.4 系统振荡且区内故障情况仿真
在稳定振荡期间,如果保护装置R有安装PSB元件,则PSB元件会将保护装置闭锁,以避免保护装置误动。在稳定振荡期间发生三相故障时,正序阻抗轨迹在阻抗保护Ⅲ段范围内。此时,由于对称性,PSB元件无法解锁保护装置R。通过将传统区域算法与MP法相结合,可以实现将保护装置R解锁。系统参数设置如2.3小节。系统振荡且区内三相故障情况的仿真结果如图5所示。
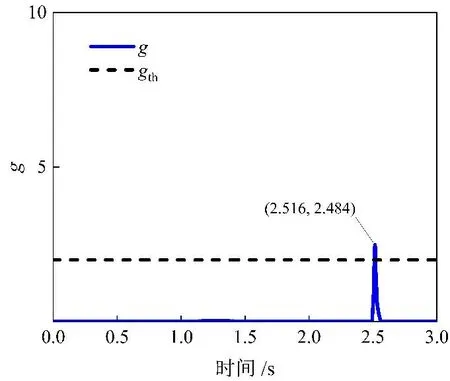
(a) 计算结果图
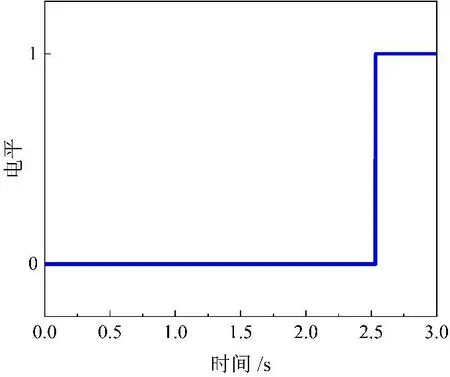
(b) 保护动作图
由图5(a)可以看出,集成算法在2.516 s时检测到三相故障F,保护装置R发出动作指令,将故障线路切除。
2.5 系统振荡且区外故障情况仿真
在图2所示系统中,在距离保护装置安装点240 km处发生三相故障,发生时刻为2.5 s,持续时间为0.5 s。系统仿真结果如图6所示。
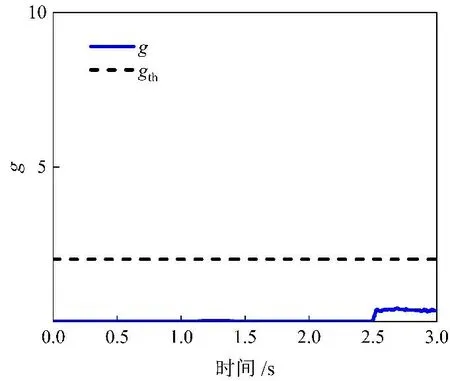
(a) 计算结果图

(b) 保护动作图
由图6(a) 可以看出,可以看出,当系统发生振荡且在振荡期间发生保护区外的三相故障时,经集成算法的计算,保护装置不会发生误动。
3 结 论
为了改善阻抗保护Ⅲ段的适用情况,提出一种瞬态监督检测函数。通过对该函数的使用,可以提高保护装置在低频振荡情况下动作的可靠性。
(1)所提出的集成算法根据重构信号与原始信号之间的误差来设置阈值,阈值不需要人为每次重新设置。集成算法可以检测电力系统在低频振荡下的多种情况;
(2)系统在仅振荡或故障的单一情况下,可以保证保护装置可靠动作;
(3)系统在振荡且分别发生区内外故障的两种情况下,可以保证保护装置可靠动作。
