基于ADAMS 的RV 减速器动态仿真分析

王春明，张 磊，张 彭，董金梅，张晓博

（1.徐州博远传动机械有限公司，江苏 徐州 221100；2.徐州工程学院 机电工程学院，江苏 徐州 221018）

随着工业机器人以及自动化技术的不断发展，多种场合对于关键传动部件的要求也越来越高[1]。RV 减速器是目前工业机器人领域应用最广的传动减速器，具有结构紧凑、传动效率高、减速比大及承载能力强等特点，与其他减速器相比，还具有一定的冲击缓冲作用。RV 减速器同时也是我国工业机器人领域发展的重要战略点。我国对RV 减速器的研究起步较晚，虽已取得一定的卓越成就，打破了日本数年前在该领域的垄断地位，但仍要不断加大其自主研究力度，不断提高相关领域在国际市场中的竞争力。

近些年来，虚拟仿真技术不断发展，通过虚拟仿真进行提升研究的技术已经十分成熟且可靠。与传统研究方法相比，通过虚拟样机仿真技术对RV 减速器进行动态仿真分析具有研究周期短、成本低、可靠性高等优点，而且能够利用多种功能对减速器的多个部件进行多层次、多方面的研究与分析，对于RV 减速器的深入研究与发展具有重要意义。

本文对RV减速器理论传动进行分析，利用ADAMS建立RV减速器虚拟样机模型，对其进行动力学仿真，获取主要零部件角速度变化曲线，将其与理论计算值对比，误差值在允许范围内，进一步验证虚拟样机模型建立的正确性，获取主要零部件受力变化曲线，进行分析，相关数据为RV减速器有限元分析提供理论依据。

1 RV 减速器理论传动分析

RV 减速器是摆线针轮机构和行星齿轮减速机构组合而成的二级减速器。主要由输入轴、针齿壳、针齿、摆线轮、左右行星架、行星轮、曲柄轴、轴承及油封等组成。其结构示意图如图1 所示。

图1 RV 减速器结构图

输入轴作为输入构件输入动力，通过与行星轮啮合传动实现第一级减速传动。行星轮与曲柄固连，2 片相位差180°的摆线轮分别套于曲柄对应偏心块上，并通过轴承与摆线轮接触。曲柄轴转动带动摆线轮绕输入轴发生转动，同时使得摆线轮分别与针齿发生接触转动而实现第二级减速传动。左右行星架通过连接件与摆线轮固连，起到支撑固定作用[2]。随着摆线轮的转动，行星架在接触力的作用下发生反向转动，与摆线轮同转速输出，最终达到减速输出的效果。理论传动比计算过程如下。

一级减速传动中，根据“机构转化法”计算出一级传动比为

式中：ns为中心轮转速，r/min；nh为行星架转速，r/min；np为行星轮转速，r/min；Zs为中心轮齿数；Zp为行星心轮齿数。

二级减速传动中，假设曲柄固定，以行星轮的自转速度为输入速度，同理利用机构转化法求出二级传动比为

式中：nd为摆线轮的转速，r/min；nr为针齿轮的转速，r/min；Zd为摆线轮的齿数；Zr为针齿轮的齿数。

摆针减速机构的齿针数总是比摆线轮的齿数多1，故有

减速器中摆线轮和行星轮通过连接件固定在一起，又有

将nr=0 带入，联立可得

本文选取的RV 减速器中心轮齿数Zs为12，行星轮Zp齿轮为42，摆线轮齿数Zd为39，针齿数Zr为40，计算所得RV 减速器传动比为140。

假设输入轴转速为1 500 r/min，根据分析可得部分构件的理论转速，结果见表1。

表1 部分构件转速理论计算结果

2 RV 减速器动态仿真分析

将RV 减速器的模型导入ADAMS 软件中，建立其虚拟样机模型，对其进行前处理设置，而后实现动态仿真，并对主要部件的角速度、接触力进行研究，为改善RV 减速器的工作性能提供可靠依据。

2.1 建立虚拟样机模型

将RV 减速器三维实体模型以Parasolid（*.x_t）格式导入仿真软件中，设置重力方向为-Y 方向，使用表格编辑器批量编辑各构件属性[3]。而对RV 减速器进行动态仿真时，预设置工作量较大，为了提高仿真效率，要对RV 减速器进行必要简化处理：删除曲柄轴、输入轴和行星架部分的轴承以及弹簧垫片，删除油封、螺栓、销等连接构件。所建立的虚拟样机模型如图2所示。

图2 RV 减速器的虚拟样机模型

为使虚拟样机模型运动，需对其零部件之间添加正确的运动副关系。零部件之间的约束关系见表2。

表2 零部件约束关系

运动副约束添加之后，为输入轴添加驱动函数F（time）=Step（time，0，0，1，9 000 d）。添加约束后虚拟样机如图3 所示。

图3 设置约束的虚拟样机模型

2.2 动力学仿真与分析

2.2.1 角速度分析

在对虚拟样机模型添加正确的运动副及驱动函数后，便可对其进行运动仿真，设置仿真分析总时长5 s，步数500 步，进行动态仿真并输出相应结果，使用ADAMS 后处理模块获取RV 减速器输入轴角速度变化曲线图如图4 所示、行星轮角速度变化曲线图如图5 所示及行星架轴角速度变化曲线图如图6 所示。

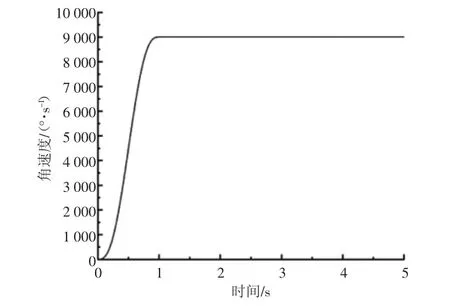
图4 输入轴角速度

图5 行星轮角速度

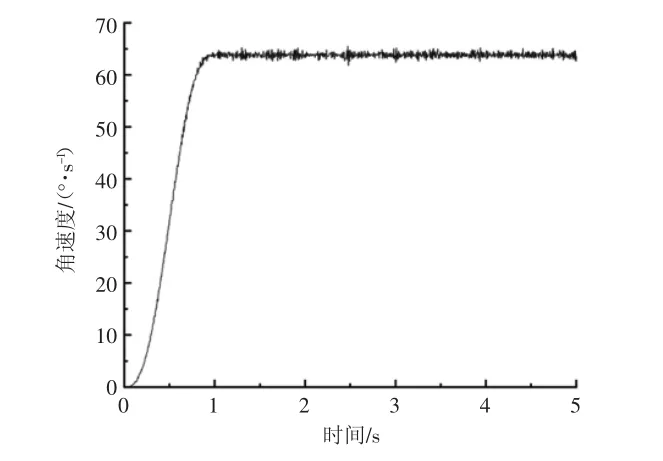
图6 行星架轴角速度

对图4—图6 分析可得，设置输入轴角速度为正值时，获取的行星轮角速度值为负值、行星架角速度值为正值[4]，说明行星轮运动方向与输入轴运动方向相反，行星架运动方向与输入轴运动方向相同，进一步说明RV 减速器传动理论分析与仿真结果一致，表明RV 减速器中各个传动部件满足RV 传动方向关系。

同时行星轮与行星架在0～1 s 阶段内都处于加速阶段，在1～5 s 内，角速度保持在一定范围内波动。对RV 减速器进行动态仿真时，在输入转速为1 500 r/min即9 000 d/s 条件下，行星轮的输出角速度最终稳定在2 500 d/s 的上下范围内波动，为了保证仿真数据的准确性，采用平均思想，行星轮角速度在1～5 s 时间段内的热点数据除去个别峰值外，其余各点均满足（2 500±125）d/s 的范围。行星架角速度最终稳定在64 d/s 的上下范围内波动，同理除去数据中的个别峰值外，其余各点均满足（64±3.2）d/s 的范围。部分零部件仿真计算结果见表3。

表3 部分零部件转速仿真与理论计算结果

由表3 可得，行星轮和行星架的输出角速度与理论算值的误差均不大于5%。以上动态仿真验证了RV减速器的减速比约为140，与理论计算值相等，证明了所建立RV 减速器虚拟样机的正确性[5]。

2.2.2 接触力分析

针齿与摆线轮的接触是二级减速中的关键环节，研究其接触力的动态变化过程，对于传动特性的研究具有重要意义。40 个针齿与2 个摆线轮共形成80 个接触力，任取一个针齿进行研究。摆线轮和针齿接触力的变化过程如图7—图10 所示。

图7 针齿与摆线轮1 在Y 方向上的接触力

图8 针齿与摆线轮1 在Z 方向上的接触力

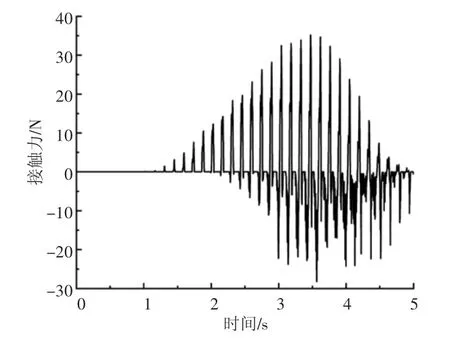
图9 针齿与摆线轮2 在Y 方向上的接触力

图10 针齿与摆线轮2 在Z 方向上的接触力

从图7—图8 分析可知，在0～2 s 内，减速器摆线轮正处于加速阶段，摆线轮运动的角速度不断增大，导致针齿与摆线的接触力在Y 向以及Z 向接触力逐渐增大[6]。2 s 左右时接触力达到最大。而后接触力逐渐减小，Z 向、Y 向接触力也逐渐减小。当减速器进入稳定运转后，针齿接触力将呈正弦式波动的周期变化。

图7、8 与图9、10 曲线峰值出现在不同时刻的原因是由于针齿与摆线轮1 和摆线轮2 接触的时刻不同。由于2 个摆线轮成相位差180°，故针齿必然先与其中一轮进行接触啮合。但由于2 片摆线轮结构相同、转速相同，所以2 组不同的接触力总体变化趋势相同，均呈现正弦式周期波动变化[7]。

输入轴中心轮与行星轮的啮合接触力动态变化如图11 所示。0～1 s 内，两轮均处于加速运转阶段，转速逐渐增大，啮合接触力也逐渐增大。1 s 之后，两轴进入平稳运行阶段，曲线呈现周期变化。

图11 输入轴中心轮与行星轮的啮合接触力

综上所述，RV 减速器在加速运转阶段，各部件间的受力波动较大。当其处于平稳运转阶段时，针齿接触力以及行星轮接触力呈周期性变化。且针齿与摆线轮交替啮合，呈现出交替承受接触力的周期运转规律，减速器仿真运动符合实际运动规律。

3 结论

本文从理论分析和仿真分析2 个层面对RV 减速器展开研究，首先通过理论分析其结构以及传动特点，计算出理论传动比以及部件的理论输出角速度。而后，通过建立起虚拟样机模型对其进行动态仿真，根据仿真结果，行星轮、行星架的输出角速度与理论计算角速度误差均小于等于5%，仿真传动比接近理论计算传动比，验证了所建立虚拟样机的可靠性。针齿接触力呈现周期性变化，存在间歇受力情况，加速阶段受力变化波动较大，符合针齿理论受力状况。针齿是RV 减速器中的关键部件，研究其接触力动态变化对提高针齿质量，提升减速器传动效率以及稳定性具有一定的意义。