融入宽范围物性约束策略的大地电磁和重力的Gramian约束联合反演

曾志文, 陈晓, 韩江涛, 郭冬, 邓居智, 张志勇, 郭一豪

1 吉林大学地球探测科学与技术学院, 长春 130026 2 东华理工大学地球物理与测控技术学院, 南昌 330013 3 安徽省勘查技术院, 合肥 230041

0 引言

地球物理反演的多解性、单一地球物理方法的局限性以及地质情况的复杂性,决定了综合地球物理研究的必要性,联合反演发挥的优势也越加突显(杨文采,2002;刘光鼎,2005;底青云等,2020).现阶段结构约束联合反演发展比较成熟,最具代表性的如基于交叉梯度方法的联合反演(Gallardo and Meju,2003;Wu et al.,2022).岩石物性约束联合反演虽然耦合效果强,但因为物性约束方式对先验信息要求更高,存在难以实施或产生有偏差的地球物理模型的风险(Tu and Zhdanov,2021),因此研究程度较低.

基于岩石物性约束的联合反演,需要建立不同岩石物性之间的理论、经验或统计相关性的关联.虽然有Faust公式(Graul,1987)可以将电阻率和速度联系起来,以及Archie公式(Archie,1942)可以将电导率和速度联系起来,还有联系地震波速和密度之间的伯奇定律(Birch,1960,1961)等,但是在联合反演中更多的是利用钻孔或测井数据来确定岩石物性参数的关联特征的(Jegen et al., 2009;Dell′Aversan et al.,2016),这也从侧面说明了岩石物性关联特征的复杂性和模糊性.针对岩石物性关联信息不易建立、适用性有限的问题,陈晓等(2016,2017)以基于模拟退火算法的 MT 和地震联合反演为例,提出了宽范围物性约束技术,随后又将宽范围物性约束技术融入“多次建模,综合约束,分步反演”的联合反演新框架中.简而言之,该约束方式将岩石物性关联融入全局优化算法的模型生成和更新环节,直接生成在一定范围内相耦合的地球物理模型参与反演运算,进而实现岩石物性参数的耦合;张磊(2016)针对岩石物性关联关系复杂的情况,提出了随机正反比的宽范围岩石物性约束方案,增加了该技术的灵活性;郭曼(2018)将宽范围物性约束技术引入到基于模拟退火算法的 MT 和重力贝叶斯联合反演当中,进一步扩展了该技术的应用范围.曾志文等(2020)实现了基于差分进化算法的MT和重力的宽范围物性约束联合反演,进一步验证了该约束方式在全局优化算法中的适用性.

上述分析可以看出,岩石物性统计特征的复杂性是客观存在的.研发容易实现的、具有一定容错性的岩石物性约束方式,是该领域的前沿和需求.宽范围物性约束技术具有在一定程度上可以降低先验信息的要求、提高岩石物性约束方式的容错率等特点,但是该技术目前只在全局优化算法中得以实现.另外,与全局优化算法相比,梯度优化算法具有计算效率高、速度快等优点,实际中应用更为广泛,然而如何将其推广至梯度优化算法联合反演至今没有明确的策略.在全局优化算法中,普遍存在解空间,易于实现将反演解限定在一定空间内.而梯度优化算法如若强制性给定解空间,则会直接影响到解的搜索.如何将范围约束融入到联合算法寻优过程,以及先验信息如何融入都是亟待解决的科学问题.

此外,Zhdanov等(2012)提出了Gramian约束方式,其本质为参与地球物理联合反演约束的向量组满足线性相关.当参与地球物理联合反演约束的向量组由物性参数向量组成时,其可视为岩石物性约束.Zhu等(2015)使用Gramian约束求解考虑剩余磁化强度下的总磁场强度(TMI)反演问题.Lin和Zhdanov(2017,2019)将该约束用于盐丘模型的速度-密度结构反演中,并且应用于实际勘探.Tu和Zhdanov(2020)开展基于Gramian约束的地震和重力联合反演方法,在黄石火山口处得到与前人研究成果相同的低密度和低速异常结果.Malovichko等(2020)通过转换算子将电导率与速度的转换关系一起写入Gramian约束中,将电阻率模型作为已知的岩石物理模型指导三维地震全波形反演,但并无涉及模型转换和范围约束等相关研究.Gramian约束对先验信息依赖较低,是比较适用于先验信息储备低的勘探新区.但若研究区域勘探程度较高,研究者储备有一定的先验信息,此时就需要可以融入先验信息的联合反演技术.以Gramian约束为例进行分析,Gramian约束是一种“松约束”,不需要明确参与约束的向量之间的关联系数,这一特点降低了Gramian约束应用的门槛,但从另一个角度分析,假如研究区域有明确的先验物性统计信息,利用这种“松约束”方式也无法将先验信息确切地融入联合反演.但若研究区域勘探程度较高,此时就需要可以融入先验信息的联合反演技术.

基于此,本文尝试提出适用于梯度优化算法的宽范围物性约束联合反演策略,并将先验信息融入到Gramian约束联合反演中,旨在提高先验信息利用率的同时,降低联合反演技术的门槛,进而为综合地球物理联合反演提供新的思路.

1 面向梯度优化算法的宽范围物性约束策略

1.1 基本思想

宽范围物性约束的基本思想是将岩石物性先验信息与所采用的优化算法相结合,不再简单地将先验物性关联映射获得的模型直接代入联合反演运算,而是在一定范围内进行再搜索,既能发挥先验物性信息的导向作用,又可以充分利用优化算法的寻优能力.

1.2 基于梯度优化算法的宽范围物性约束策略

如何将宽范围物性约束思维融入梯度优化算法中是值得挑战的.本文提出了适用于梯度优化算法的“模型转换、范围约束、耦合项”的宽范围物性约束基本策略,可见示意图1,具体如下:

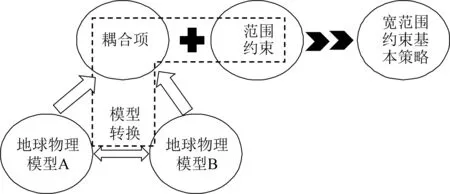
图1 宽范围物性约束策略示意图Fig.1 Schematic diagram of wide-range petrophysical constraints

第一,先验物性关联为导向.这一点与全局优化算法的宽范围物性约束是一致的,但是引入的方式不同.在全局优化算法中,可以直接利用物性关联实现不同地球物理模型的转换(陈晓等,2016).而在梯度优化算法中,可以将物性转换之后模型作为初始模型,或者可以将物性转换之后的模型写入联合反演目标函数中.

第二,耦合项.正如典型的耦合方式,交叉梯度、Gramian约束、余弦相似度(Shi et al.,2018)等,在以往的文献中学者们都是使用梯度、共轭梯度或者牛顿法等来实现关于耦合项的目标函数的极小化.可以看出,这种带有耦合项的方式更适合于梯度优化算法.因此有必要将典型的耦合方式引入,进一步提高梯度优化算法联合反演结果的耦合效果.需要指出的是,以Gramian约束为例,传统的Gramian约束不需要明确参与约束的物性向量之间的相关系数,这既是其优点,也同样是缺点.正是因为它不需要确定这些相关系数,所以即使有明确的先验关联信息,也无法将这些系数的信息以及实际中的约束关系,引入到联合反演中来.因此,目前这些典型的耦合方式都无法将明确的先验信息融入联合反演.

第三,范围约束.与全局优化算法本身就需要设置待解参数的解空间不同,梯度优化算法是根据目标函数的梯度来更新地球物理模型,一般需要确定解更新的方向和步长.梯度优化算法在实现的过程中,如早期采用的最简单的约束方式,人为地不顾梯度方向,直接限制解的上下限,但这样的操作会直接影响解的搜索.故此,基于梯度优化算法的宽范围物性约束需要可以将解限制在一定范围内的方法技术,如:惩罚函数(Kim et al.,1999),对数转换(Commer and Newman,2008)等.

2 宽范围约束联合反演的实现

2.1 目标函数及实现

以MT和重力联合反演为例,介绍面向梯度优化算法的宽范围物性约束策略的具体实现.基于惩罚函数的Gramian约束联合反演目标函数可写为:

(1)

其中,Pα(m(1),m(2))表示目标函数;m表示模型参数向量;φ(i)表示数据拟合泛函;sMN表示模型稳定泛函;α表示正则化因子;β是Gramian约束项的权重系数;sG是Gramian约束耦合项;μ是惩罚函数项的权重系数;P(m(i))是惩罚函数约束项.

2.1.1 Gramian约束

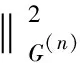
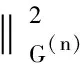
(2)

转换算子T可以最简单地取为单位阵,此时就是基于岩石物性线性关联的约束.

2.1.2 范围约束

已有研究表明,虽然惩罚函数法需要确定惩罚函数的权重系数,但更加灵活,适用于物性关联特征复杂的情况(陈晓等,2023).基于此,本文采用惩罚函数法来实现物性参数的范围约束.

模型参数向量满足约束范围:

ak≤mk≤bk,

(3)

其中ak和bk分别表示模型参数mk的最小值和最大值.将其以罚函数的形式写入到目标函数当中,有:

(4)

其中,P为惩罚函数约束项,q是不等式的总数,对于上述不等式(3),在这里q=2,hi(mk)的形式为:

h1(mk)=mk-ak,

(5)

h2(mk)=bk-mk.

(6)

显然,若模型参数向量满足式(3),那么不等式约束项等于0,即不起作用.当超出界限范围时,才会起到约束作用.

2.2 宽范围约束联合反演的流程

MT和重力的宽范围物性约束联合反演的流程图可参见图2.本文拟以联合反演的重力结果为例,探讨宽范围物性约束策略的效果.如图2的右半部分所示,介绍如下:

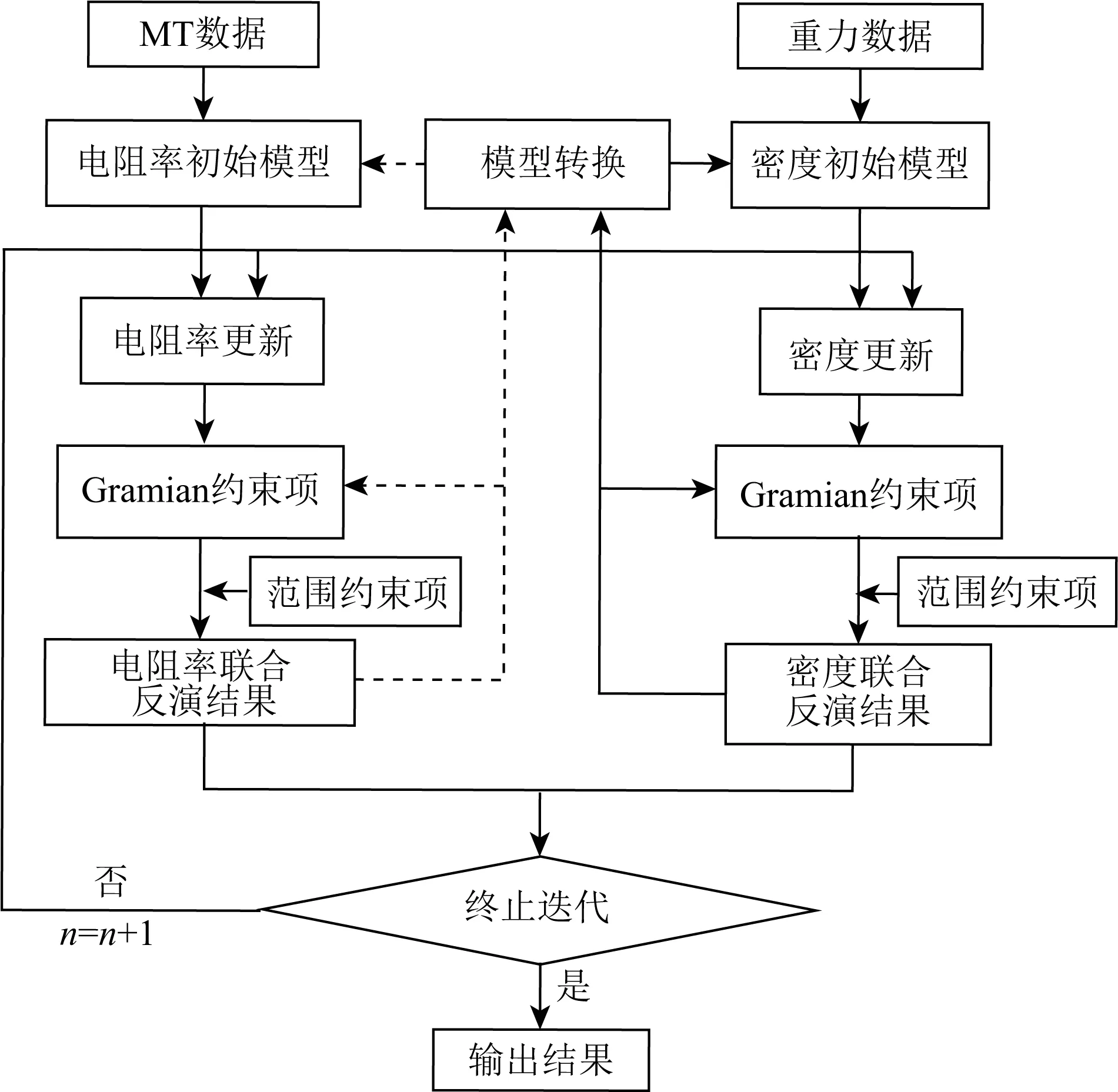
图2 联合反演流程图Fig.2 Flow chart of joint inversion

(1) 首先利用MT数据进行单独反演,得到电阻率结果.

(2) 根据岩石物性关联的先验信息,由电阻率结果映射到密度模型,并将此模型作为初始模型引入到密度联合反演.

(3) 利用电阻率结果和密度模型计算Gramian约束项,并加入范围约束项,将密度的先验信息分布范围用于约束密度联合反演过程.

(4) 密度更新,是否达到最大迭代次数,否则重复步骤(3)和(4),是则进入下一步.

(5) 输出密度联合反演结果.

3 模型试验

3.1 “精准”先验信息模型试验

为了验证宽范围约束在梯度优化算法联合反演中的效果,首先设计了在先验信息“精准的”下的模型试验.真实模型见图3a和3b,在背景值为100 Ωm、0.01 g·cm-3的均匀半空间中,存在两个异常体,从左到右剩余密度分别为0.2、0.05 g·cm-3,电阻率值分别为5、20 Ωm,密度约束范围给定为[0,0.2].图4e中的黑线是MT和重力岩石物性的先验信息关联.可以看到,此时的先验信息是相对“精准的”.首先,对MT数据进行40次的单独反演,得到电阻率反演结果图3d.然后,通过先验物性关联映射得到密度联合反演的初始模型,再进行联合反演.

图3 二维电阻率和剩余密度简单块体模型(a) 剩余密度模型; (b) 电阻率模型; (c) 第一次迭代密度联合反演结果; (d) 电阻率反演结果.Fig.3 Two-dimensional resistivity and residual density simple block model(a) Residual density model; (b) Resistivity model; (c) Density joint inversion result of the first iteration; (d) Resistivity inversion result.

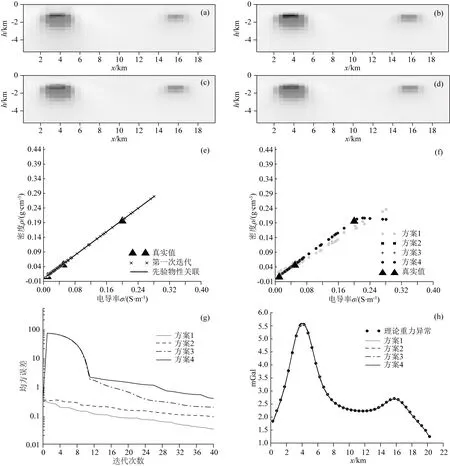
图4 精准先验信息下的4种方案反演结果(a) 方案1密度联合反演结果; (b) 方案2密度联合反演结果; (c) 方案3密度联合反演结果; (d) 方案4密度联合反演结果; (e) 第一次迭代物性耦合图; (f) 物性耦合图; (g) 均方误差曲线; (h) 重力异常拟合曲线.Fig.4 Inversion results of four schemes with precise prior information(a) Density joint inversion result of Scheme 1; (b) Density joint inversion result of Scheme 2; (c) Density joint inversion result of Scheme 3; (d) Density joint inversion result of Scheme 4; (e) Petrophysical coupling diagram of the first iteration; (f) Petrophysical coupling diagram; (g) Mean square error curves; (h) Gravity anomaly fitting curves.

基于上述基础,设计了4种对比试验方案(见表1).具体而言:方案1,不加Gramian约束项和不加惩罚函数的密度联合反演;方案2,加Gramian约束项和不加惩罚函数的密度联合反演;方案3,不加Gramian约束项和加惩罚函数的密度联合反演;方案4,加Gramian约束项和加惩罚函数的密度联合反演.需要指出的是,为了更单纯地对比惩罚函数项、Gramian约束项对联合反演效果的影响,本文在电阻率反演中暂不考虑密度结果的耦合效果,即关闭了密度对电阻率的耦合通道,进而保证密度联合反演在相同的条件下进行.

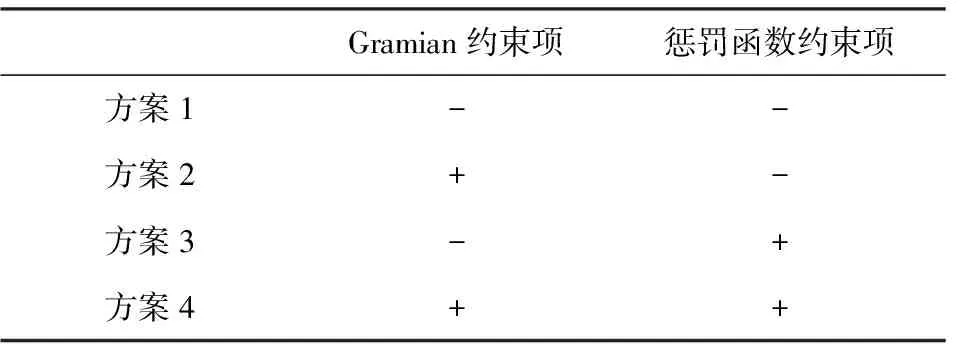
表1 4种联合反演方案Table 1 Four joint inversion schemes

图3c是4种方案的第一次迭代结果,图4e中叉号点是其对应的物性耦合图.可以看到,由于先验信息是相对“精准的”,第一次迭代时的密度和电阻率已经获得较好的耦合.在方案1(不加Gramian约束和不加惩罚函数约束)的条件下,密度联合反演结果(图4a)以及耦合图(图4f中的灰圆点)显示,密度和电阻率的耦合呈现线性关系但偏离了真实分布,而且存在密度联合反演结果超出了密度先验信息范围的情况;方案2(只加Gramian约束)的条件下,密度联合反演结果(图4b)以及耦合图(图4f中的矩形点)显示,密度和电阻率分布是相关的,但也存在密度超过先验信息范围的现象;在方案3(只加惩罚函数约束)的条件下,密度联合反演结果(图4c)以及耦合图(图4f中的加号点)显示,密度值被有效地约束在范围之内;在方案4(加Gramian约束和加惩罚函数)的条件下,密度联合反演结果(图4d)以及耦合图(4f中的黑圆点)显示,密度和电阻率分布是相关的,且密度值被有效地约束在范围之内.

由上述分析,Gramian约束和惩罚函数是有效的,在先验信息“精准的”情况下,可以实现物性参数在一定范围内进行耦合,也验证了宽范围约束策略在梯度优化算法中的有效性.

3.2 “不精准”先验信息的简单模型试验

上述3.1节验证了宽范围约束策略在先验信息“精准的”情况下的有效性,本节则在先验信息“不精准的”情况下,验证宽范围约束策略的效果.设计的真实模型与3.1节一样,图6e中的黑线是MT和重力岩石物性的先验信息关联.可以看到,此时的先验信息是“不精准的”.同样,首先对MT数据进行40次的单独反演,得到电阻率反演结果图5b.然后通过先验物性关联映射,得到密度联合反演的初始模型,采用和3.1节相同的4种对比试验方案.本节所有图件色标也与3.1节模型试验一致.

图5 初步的单独反演结果(a) 第一次迭代密度联合反演结果; (b) 电阻率反演结果.Fig.5 Preliminary separate inversion results(a) Density joint inversion result of the first iteration; (b) Resistivity inversion result.

图5a是4种方案的第一次迭代结果,图6e是对应的第一次物性耦合图.此时,由于先验信息是相对“不精准的”,第一次迭代时的密度和电阻率的耦合是偏离真实物性值分布的.在方案1(不加Gramian约束和不加惩罚函数约束)的条件下,密度联合反演结果(图6a)不能较好地反映异常体的位置,耦合图(图6f中的灰圆点)分布较乱,且偏离了真实物性的分布;方案2(只加Gramian约束)的条件下,密度联合反演结果(图6b)较好地还原了两个异常体的位置,耦合图(图6f中的矩形点)显示密度和电阻率分布是相关的,但存在密度超过先验信息范围的现象;

在方案3(只加惩罚函数约束)的条件下,密度联合反演结果(图6c)以及耦合图(图6f中的加号点)显示,密度值被有效地约束在范围之内,但这个物性耦合显然是受“不精准”的先验关系所影响;在方案4(加Gramian约束和加惩罚函数)的条件下,密度联合反演结果(图6d)以及耦合图(图6f中的黑圆点)显示,密度和电阻率分布是相关的,且密度值被有效地约束在范围之内,较好地还原了真实模型.

由上述分析可以看出,宽范围约束策略在先验信息“不精准的”情况下也是适用的.它可以更好地促进物性参数在一定范围内进行耦合,进一步提高了岩石物性关联约束方式在梯度优化算法中的适用性,并且具有一定的容错率,可以降低对先验信息的要求.

3.3 “不精准”先验信息的复杂模型试验

为了进一步验证宽范围约束策略在复杂模型中的效果,本节设计了复杂的4个块体试验.在背景值为200 Ωm、0.01 g·cm-3的均匀半空间中,存在4个异常体,从左到右剩余密度分别为0.4、0.1、0.05、0.04 g·cm-3,电阻率值分别为5、20、40、50 Ωm,密度约束范围给定为[0,0.4].图8e中黑线是MT和重力岩石物性的先验信息关联,模拟的是实际中可能获得的“不精准”的物性关联的情况.与上文一样,对MT数据进行40次的单独反演,得到电阻率反演结果图7d.然后,通过黑线的先验物性关联映射,得到密度联合反演的初始模型.和3.2节一样,设计相同的4种对比试验方案.

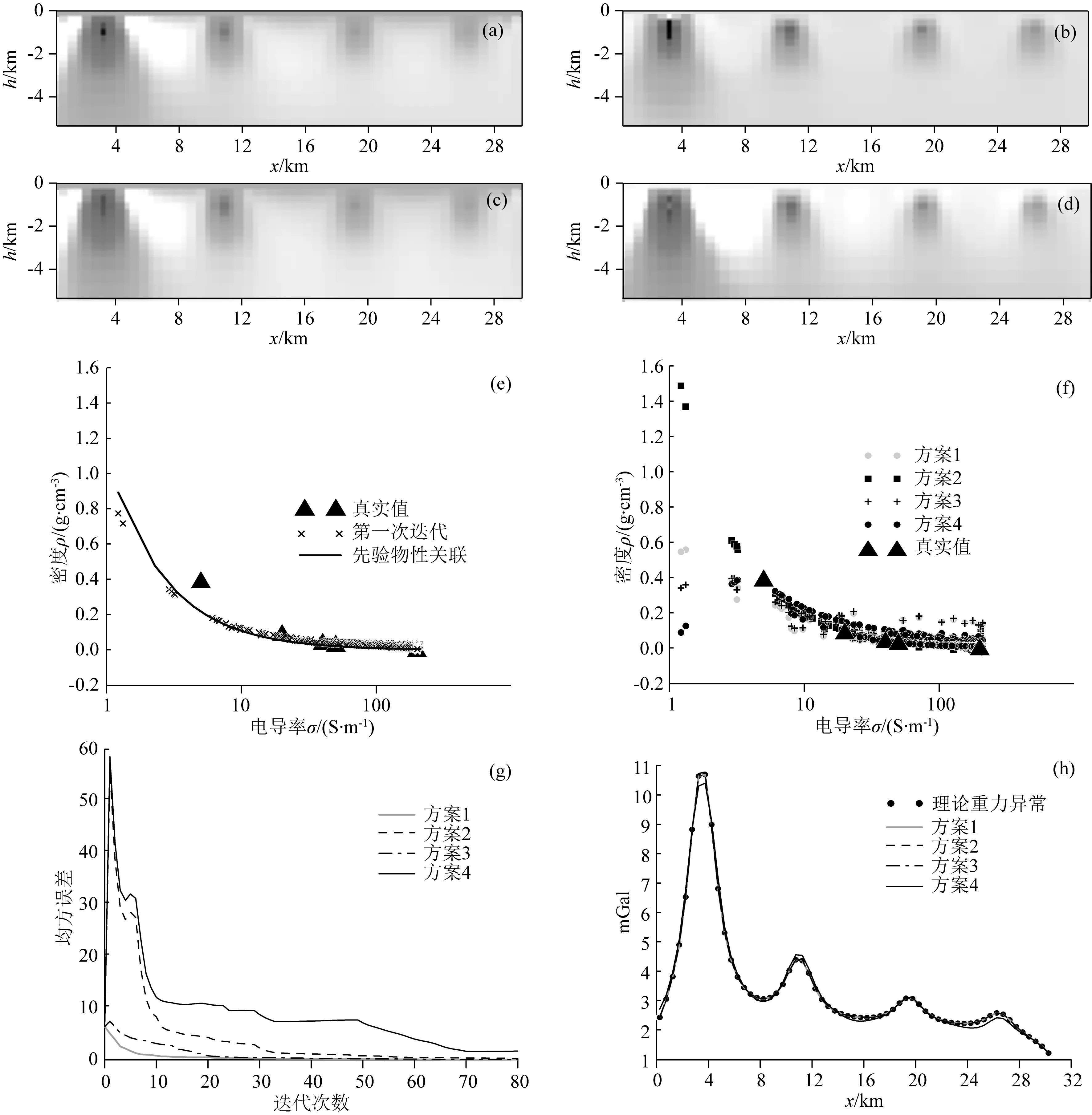
图8 复杂模型的4种方案反演结果(a) 方案1密度联合反演结果; (b) 方案2密度联合反演结果; (c) 方案3密度联合反演结果; (d) 方案4密度联合反演结果; (e) 第一次迭代物性耦合图; (f) 物性耦合图; (g) 均方误差曲线; (h) 重力异常拟合曲线.Fig.8 Inversion results for four schemes of complex models(a) Density joint inversion result of Scheme 1; (b) Density joint inversion result of Scheme 2; (c) Density joint inversion result of Scheme 3; (d) Density joint inversion result of Scheme 4; (e) Petrophysical coupling diagram of the first iteration; (f) Petrophysical coupling diagram; (g) Mean square error curves; (h) Gravity anomaly fitting curves.

图7c是4种方案的第一次迭代密度联合反演结果,图8e是对应的第一次迭代的物性耦合图.由于先验信息是相对“不精准的”,第一次迭代时的密度和电阻率的耦合也是偏离真实物性值分布的.与3.2节的模型试验规律类似,在没有Gramian约束的情况下,方案1(图8f灰圆点)和方案3(图8f加号点)的物性耦合较差,偏离了真实值分布;在有Gramian约束的情况下,方案2(图8f矩形点)和方案4(图8f黑圆点)密度和电阻率的耦合关系得到了加强,且分布在真实值附近,而再相比于方案2,加上惩罚函数的方案4密度值被有效地约束在范围之内.但图中部分数据点也显示出严重偏离,这是因为本文采用的是单向的密度顺序联合反演,电阻率结果在密度联合反演时不会更新.输入不准的电阻率信息反演结果,导致了部分数据的偏离.

可以看出,宽范围约束策略适用于复杂的地球物理模型.总而言之,本文尝试利用岩石物性关联获得初始模型,并利用惩罚函数开展范围约束,成功实现了基于梯度优化算法的宽范围物性约束联合反演.

4 实际资料处理

茶亭矿区位于南陵—宣城区域盆地内,是该区域近些年来找矿的重大发现.燕山期强烈的构造-岩浆活动使该区受到岩浆-热液作用的叠加改造,为区内矿床的形成创造了有利条件(肖庆玲等,2018;陶龙等,2019).矿区大部为中分村组火山岩覆盖,主要围岩成分为花岗闪长岩,还有各类侵入岩体等.根据参考文献(洪大军等,2019),茶亭矿区的部分矿石平均密度和平均电阻率见表2.图9是通过岩石物性统计表2建立的电导率和剩余密度岩石物性关联图,鉴于此区域的岩石物性关系比较杂,本文利用了两种不同函数关系进行拟合.

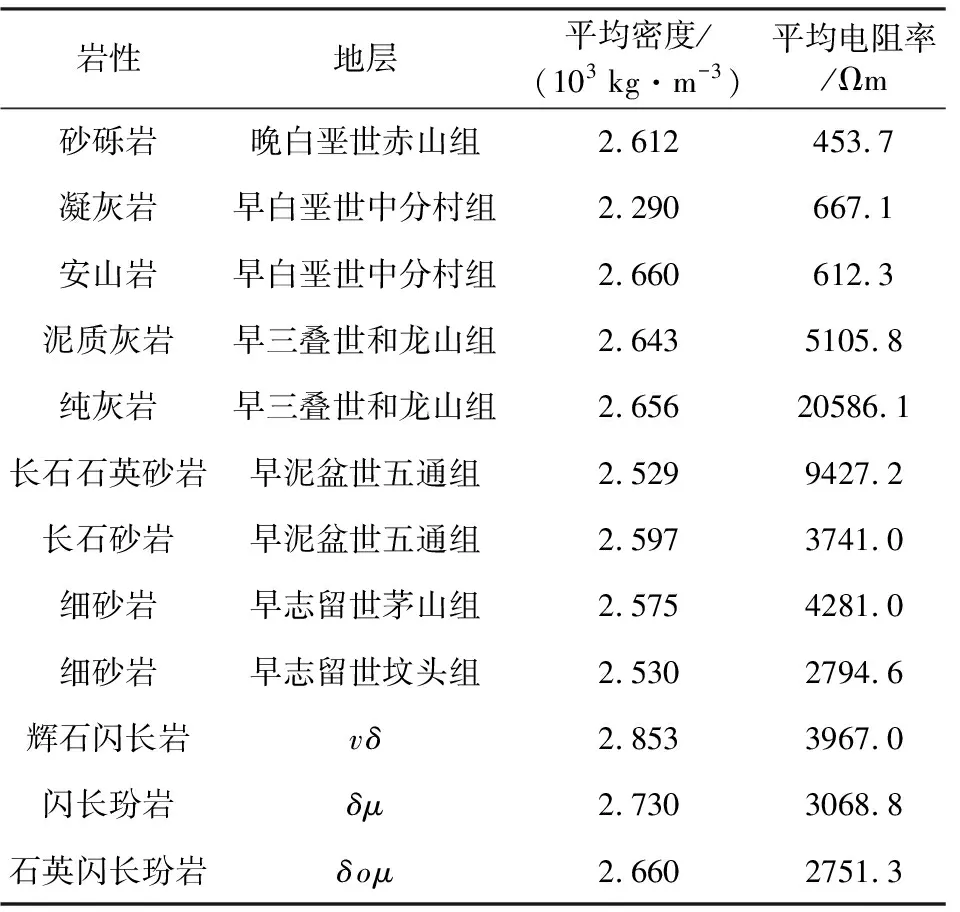
表2 茶亭矿区部分岩石物性参数Table 2 Some petrophysical parameters in the Chating mine area

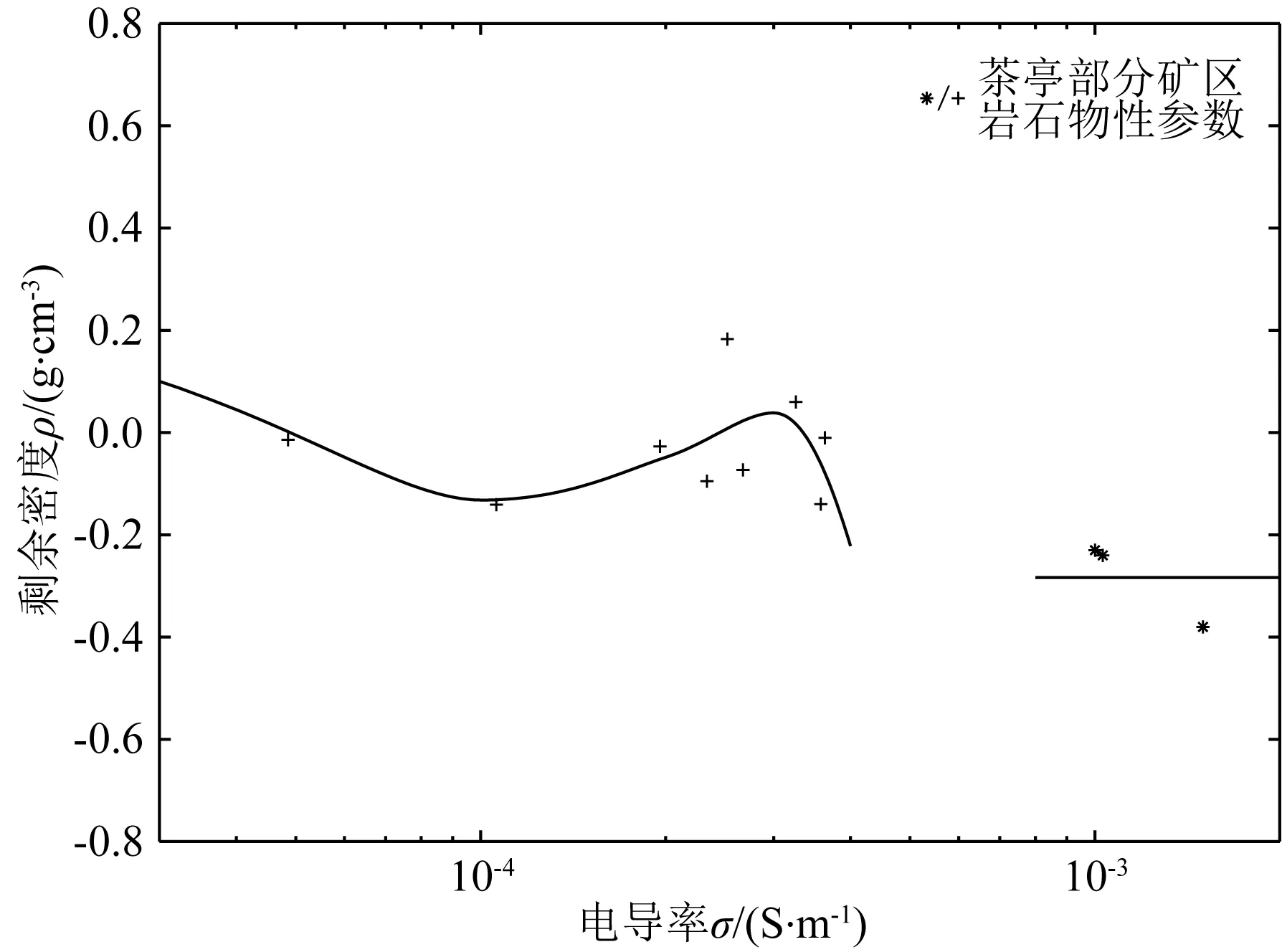
图9 电导率和密度的岩石物性关联图Fig.9 Petrophysical parameters correlation diagram of the conductivity and density

4.1 先验地质地球物理模型

图10a是由安徽省勘查技术院提供的茶亭区域的地质解译图,该结果是结合重磁反演、地质模型、钻孔数据的解译而来.谢巧勤等(2020)指出茶亭铜金矿床的矿体主要赋存于石英闪长玢岩侵入体(壳幔混源,且以幔源为主)包孕的角砾岩筒中,并根据地球化学的手段分析其为角砾岩型矿床.田自强(2020)指出茶亭铜金矿床的石英闪长玢岩是在侵位之后短时间内被隆升至近地表,再覆盖中分村组火山岩.此外,钻孔资料显示稻山村逆断层上盘的花岗斑岩为无根岩体,指示该无根岩体不是原地侵位的产物,应是逆断层活动过程中从深部运移而来的某个岩体的一部分.

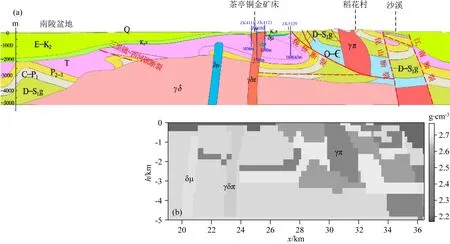
图10 先验模型(a) 地质解译图; (b) 密度参考模型.Fig.10 Priori model(a) Geological interpretation map; (b) Density reference model.

可以看出,图10a基本符合实际地质地球物理情况,具有较高的合理性且有明显的地质含义,可以作为本文开展地球物理联合反演的先验地质地球物理模型.图10b是依据地质解译图及表2的岩石物性统计表建立的密度参考模型.但此模型只有浅部5 km以上的密度构造,并没有5 km以下的信息.

图11a是对该测线的MT数据进行二维单独反演得到的电阻率结果.结合参考模型5 km以上的信息分析(图中的黑线代表构造线),可以看出,在19～24 km处的浅部两个侵入岩体处大致呈现中高阻反映,但茶亭矿床处侵入岩体的电性连通性不强,并且30～36 km处的稻山村的浅部和沙溪深部的岩体对应性有待进一步验证.

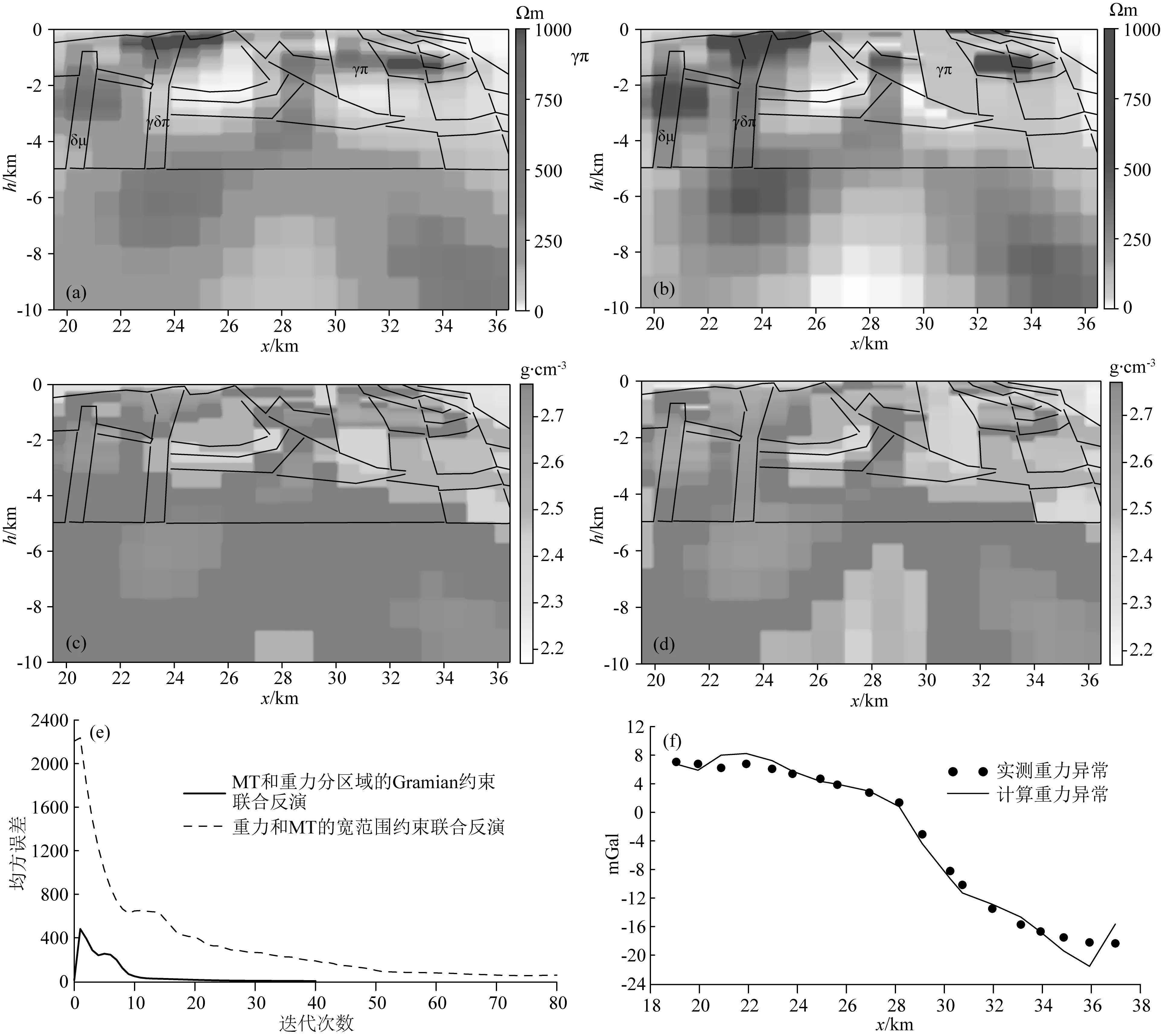
图11 联合反演结果(a) 电阻率单独反演结果; (b) 电阻率联合反演结果; (c) 密度初始模型; (d) 密度联合反演结果; (e) 均方误差曲线; (f) 重力异常拟合曲线.Fig.11 Joint inversion results(a) Separate inversion result of resistivity; (b) Joint inversion result of resistivity; (c) Initial density model; (d) Density joint inversion result; (e) Mean square error curve; (f) Gravity anomaly fitting curve.

综上分析,目前该测线还存在许多待解决的问题:茶亭矿床附近钻孔不足2 km, 茶亭铜金矿床的“根”在哪,在深部该矿床是如何展布的还是未知;另外无“根”的花岗斑岩的源在哪;此外,先验地质地球物理模型深度仅有5 km,在探索深部构造的同时,能否把先验模型也融入进去.下一步,本文将针对以上问题,运用第2节所提出的新技术来处理该测线,尝试获得新的认识.

4.2 联合反演

为了将先验地质地球物理模型融入联合反演,结合上文所提出的宽范围约束联合反演新策略,本文设计了如下的实际资料反演方案.首先,将图11a的MT单独反演结果作为联合反演的电阻率初始模型,开展基于分区域的Gramian约束MT和重力联合反演(郭一豪,2020).所谓分区域,是指电阻率模型和密度参考模型在5 km以上做Gramian约束,而5 km以下则不做要求.在迭代40次之后,得到此次电阻率联合反演结果图11b.

接下来,按照新技术反演流程图2的步骤,将上述的电阻率反演结果作为联合反演的电阻率初始模型,通过图9的先验关系映射得到密度的初始模型图11c.密度模型的约束范围如下:5 km以上的给予紧约束,将初始模型密度值上下扰动±0.02 g·cm-3;5 km以下则给定比较宽松的约束范围±0.2 g·cm-3.最后,结合图11b的电阻率反演结果,开展基于宽范围物性约束的重力和MT联合反演,迭代80次.

对比图11a和11b可以看到,图11b的19～20 km处,侵入岩体形态更加连续和清晰,在23～24 km处,铜金矿床在浅部5 km以上连通起来,这与先验信息相符.另外,在30～36 km、深度0～5 km处存在两个电阻率相对应的区域,结合密度联合反演结果图11d,推覆体的密度与沙溪深部的密度分布也是对应的.据以上分析,此处构造岩体应该是推覆构造的产物,推测与沙溪深部岩体是同源的.此外,侵入岩体的5 km以下的形态也得到了揭示,呈现出倒立的长钟状.

综上分析,本文提出的联合反演新策略,成功地将先验模型融入综合地球物理解释.联合反演结果所揭示的砾岩筒型铜金矿床在浅部的分布符合先验信息,验证了稻山村逆断层上盘无根的花岗斑岩为区域的推覆运动的产物,勾勒了角砾岩筒矿床在深部的空间分布形态,为茶亭铜金矿床深部找矿提供了深部模型.

5 结论

本文提出了适用于在梯度优化算法的宽范围物性约束策略,通过岩石物性关联生成初始模型的方式引入先验信息,在范围约束项和耦合项的共同作用下进行联合反演,使得联合反演既依赖于先验模型信息,又可以在一定程度上“摆脱”先验信息的严格控制,从而使岩石物性参数在真实值附近实现耦合.基于此,开展了模型试验和实测资料反馈,验证了新策略的适用性和实用性,具体而言:

(1) 宽范围物性约束不仅是一种技术,更是一种思维.宽范围约束策略可以提高先验岩石物性信息利用率,并降低不精确先验信息带来的风险.可以在一定程度上将先验岩石物性关联融入联合反演的迭代寻优过程,且使岩石物性耦合在一定范围内.

(2) 本文提出的“岩石物性关联+范围约束+耦合项”的思维具有较强的适用性,并且具有结合其他优化算法和约束方式进一步扩展的潜质.

(3) 本文提出的宽范围物性约束策略具有一定的实用性,新方法验证了茶亭铜金矿床浅部的分布形态,无根的花岗斑岩为推覆构造的结果,勾勒了茶亭铜金矿床的深部结构的空间展布.

需要指出的是,第一,如何将宽范围物性约束思维拓展到其他的地球物理联合反演耦合方式中去,还需要进一步试验,以及如何将新的地球物理联合反演技术推广至多地球物理方法的联合反演也值得进一步研究;第二,实测资料处理显示,Gramian约束可以实现先验信息的融入,也为该地区的地质解译提供了新视角和新思路.但是,如何评判先验信息可靠性以及如何更合理地实现先验信息的融入是值得进一步探讨的.