以结构化视角探究四边形概念本质——“四边形的认识”的教学实践与思考

□支丹婷 钟立

【课前思考】

《义务教育数学课程标准（2022 年版）》提出，要注重教学内容的结构化，要求教师“重视对教学内容的整体分析，帮助学生建立能体现数学学科本质、对未来学习有支撑意义的结构化的数学知识体系”。通过结构化教学，将学习水平、学习策略、学习内容相近的知识整合为一个教学主题，可以帮助学生学会用整体的、联系的、发展的眼光看问题，发展学生的核心素养。

以“四边形的认识”的教学为例。在编排方式上，人教版教材分三次编排“四边形的认识”的教学内容：（1）一年级下册“认识图形（二）”单元，直观认识长方形、正方形，能够辨认区分；（2）三年级上册“长方形和正方形”单元，从边和角的角度认识长方形和正方形的特征；（3）四年级上册“平行四边形和梯形”单元，从边的角度认识平行四边形和梯形。知识结构呈螺旋式上升。在概念界定上，采用“属加种差”的方式定义“正方形、长方形、平行四边形、梯形”等的概念。其中，“属”指它们都属于四边形，“种差”指它们之间的差异。如梯形是只有一组对边平行的四边形，平行四边形是两组对边分别平行的四边形。这些图形在本质上既有共同点，又有差异性。

基于此，笔者整合三年级上册“四边形”相关教学内容与四年级上册“平行四边形和梯形”相关教学内容，构建“四边形的认识”的教学，让学生在共性的探寻中理解四边形的概念，在差异的比较中建立不同四边形之间的关系，形成四边形概念的结构化，优化数学知识的认知结构，发展数学思维。具体教学目标如下：

（1）通过观察、辨认、判断四边形，知道四边形是由四条边、四个角组成的平面封闭图形。

（2）经历操作、探究、交流等数学活动，掌握长方形、正方形、平行四边形、梯形的特点，知道图形间的联系并能按一定的标准分类。

（3）结合概念学习过程，发展抽象能力和空间意识，认识数学知识之间的联系，在整体感知中形成知识结构。

【教学实践】

一、创设情境，认识四边形概念的共性

教师用课件呈现图1。

图1

师：这些是什么图形？

生：这些都是立体图形。

师：这些立体图形的每个表面都是什么图形？

生：平面图形。

师：是的。面是体的一部分，我们可以从立体图形中提取出平面图形。

教师用课件动态展示提取平面图形的过程，如图2所示。

图2

师：在下面的平面图形中，有四边形吗？

教师用课件呈现图3。

图3

师：你们能将这些平面图形分成四边形和非四边形吗？

生：我认为②⑤⑥⑨⑩⑪号图形是四边形。

师：这些四边形有什么共同点？

生：都有四条直的边和四个角。

生：四条边连起来构成了封闭图形。

师：其他图形为什么不是四边形呢？

生：④号图形是一个圆，⑦号图形的角是弧形的。

生：我觉得⑧号图形不是四边形，因为它不止四条边和四个角；⑫号也不是，它有一条边是曲线。

师：那⑬号图形是四边形吗？

生：我觉得⑬号图形不是四边形，它看起来有点奇怪。

生：我认为⑬号图形是四边形。它虽然形状奇怪，但是它有四条边和四个角，而且还是封闭图形。

师：是的，有四个角和四条直的边，就是四边形。⑬号图形属于凹四边形，其他都是凸四边形，小学阶段我们只研究凸四边形。现在大家认识了四边形，四边形有什么特点？

生：四边形有四条直的边和四个角。

师：你知道这些四边形的名称吗?

生：我知道②号图形是长方形，⑪号图形是正方形，⑨号图形是平行四边形。

生：⑩号图形是梯形。

生：⑤号图形是菱形。

师：那⑥号图形就是一般四边形。

设计意图：在一年级下册“认识图形（二）”单元的学习中，学生已经初步认识了立体图形与平面图形，能够区分长方形、正方形等平面图形，初步学习了在立体图形上找平面图形。根据课前测试，到了三年级，学生基本上能正确找出正方形和长方形，约95%的学生能找出平行四边形和梯形，这说明大部分学生对四边形有较好的直观认识。但他们不能从边、角两个维度全面描述图形的特点。据此，教师从学生现实起点出发，通过创设情境，让学生从“体”中提取出“面”，从而认识四边形概念的共性。

二、操作对比，体会四边形概念的异同

1.教师组织学生开展“搭四边形”活动。

活动要求：

（1）同桌合作从图4 的8 根小棒中选出4根搭一个四边形。

图4

（2）量一量、比一比，比较所搭四边形的边和角的特征。

（3）同桌交流，记录发现。

2.学生动手操作，教师巡视指导，收集有代表性的学生作品。

教师用课件呈现学生作品，如图5 所示，引导学生交流讨论。

图5

师：老师收集了同学们的典型作品，这些图形有什么相同点和不同点？

生：相同点是它们都有四条直的边和四个角，都是四边形。

生：根据它们的形状，我知道①⑥是长方形。

师：什么样的图形叫作长方形？

生：长方形的上下两条边、左右两条边长度相等，四个角都是直角。

师：同学们真会观察！像这样对边相等，四个角都是直角的四边形，就叫作长方形。

生：④号图形是正方形，它的四条边都相等，四个角都是直角。

师：正方形有什么特点？

生：正方形的四条边都相等，四个角都是直角。

师：你们仔细看看，⑤号图形是正方形吗？

生：我觉得不是，⑤号图形的角都不是直角。

生：⑤号图形是菱形。

师：那菱形和正方形有什么相同点和不同点呢？

生：菱形和正方形的四条边都相等，不同的是正方形有四个直角，而菱形没有直角。

师：你们还知道什么？

生：我知道②③⑦⑧这几个图形是平行四边形。

师：大家认识平行四边形吗？平行四边形有什么特点？

生：平行四边形也是对边相等。但不一样的是，平行四边形没有直角。

师：请同学们用小棒搭一搭平行四边形，想一想，搭平行四边形时要注意什么？

生：我们在挑选小棒时需注意，上下两条边要用同样长的小棒，左右两条边也要用同样长的小棒。

师：还剩下⑨号图形，有同学认识吗？它有什么特点？

生：⑨号图形是梯形，上下两边不一样长，左右两边一样长。

师：是的，⑨号图形是梯形，还是一个等腰梯形，左右两边是一样长的。梯形还有其他形状，也可以所有边都不相等。

教师用课件呈现图6。

图6

师：通过动手操作、交流讨论，我们发现长方形、正方形、平行四边形、梯形各有各的特点。你能将这些图形分类吗？它们之间有怎样的关系？

教师让学生先独立思考自行完成分类，再与同桌交流可以按什么样的标准分类，它们之间有怎样的关系。

师：哪个小组愿意来分享？

生：我们小组根据是否有直角，将这些图形分为两类，正方形和长方形为一类，菱形、平行四边形和梯形为一类。

生：我们小组根据四条边是否相等，将这些图形分为两类，正方形和菱形为一类，长方形、平行四边形和梯形为一类。

师：你们能用画图的方式表示这些图形之间的关系吗？

其中一个小组的学生拖动图形进行演示，呈现图7，并进行说明。

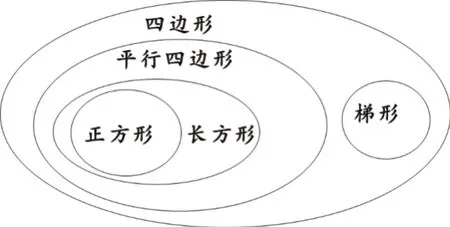
图7

设计意图：学生已经有了折一折、比一比的基本活动经验，这些操作活动是探究四边形特征的重要方法。教师利用操作活动，引导学生给不同的四边形分类，帮助学生对长方形、正方形、菱形、平行四边形、梯形等概念形成初步认识，挖掘各个四边形概念的异同，建立不同四边形之间的内在联系。

三、建构联系，感悟四边形概念的本质

师：大家通过探究，认识了长方形、正方形、菱形、平行四边形和梯形，知道了它们边和角的特点。这些特殊的四边形形状都不一样，图5 中，哪些图形可以通过变化，变为和其他图形一样的四边形？

生：沿对角两个点拉动①号长方形，可以将其变为平行四边形；用同样的方法，也可以把②号、③号平行四边形变为长方形。

师：你真善于发现！长方形和平行四边形是可以通过拉伸互相变化的。

生：我还发现，只要拉一拉⑤号菱形，就能把它变成正方形。因为菱形和正方形的四条边都相等，所以只要把菱形的角变成直角，菱形就成了正方形。因此也可以说正方形是特殊的菱形。

师：还有其他发现吗？

生：把⑥号长方形的两根长小棒换成两根短小棒，就变成了一个正方形。

师：大家通过再一次动手操作，把一个图形变成了另一个图形。图形世界很奇妙，它们有相同的特征，也有各自不同的特点。这些图形在本质上有着内在的联系。

教师用课件动态呈现图形之间的联系，如图8所示。

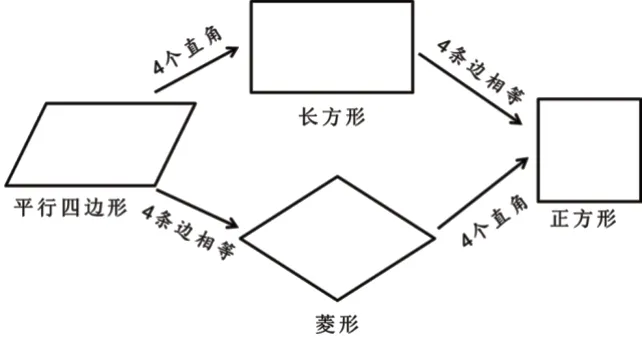
图8

设计意图：让学生在对不同四边形的感知的基础上，体会不同四边形之间的区别；在“边”和“角”的变化中，理解不同四边形之间的内在联系。通过“辨”与“变”，提升学生的空间想象力，发展空间观念。

四、多元联结，丰富四边形概念的结构

师：同学们，大家通过学习探究，认识了很多特殊的四边形，现在请你来猜一猜，老师手里的图形是什么？

教师呈现图9。

图9

生：可能是三角形、梯形、正方形、长方形。

师：如果这是一个四边形，有可能是什么图形？

生：是四边形，又有一个直角，那么可能是梯形、正方形、长方形。

师：这个四边形有两个直角，猜猜是什么图形？

教师呈现图10。

图10

生：我觉得可能是正方形和长方形，还有可能是梯形。

师：看来还不能确定，那再增加一个角，有三个直角，猜猜是什么图形？

教师呈现图11。

图11

生：有三个直角，且相邻两条边一样长，肯定是一个正方形。

设计意图：利用“猜图形”活动，让学生通过理解四边形概念的共性和不同，抓住不同四边形图形的本质属性进行辨析，进一步理解不同四边形之间的内在联系，构建四边形概念的知识结构，发展数学思维。