关联代数上零点可导映射的刻画

莫增崇

(吉林师范大学 数学与计算机学院,吉林 四平 130000)

0 引言

关于代数在零点处的可导映射的研究一直是诸多学者关注的焦点[1-6]。朱军[7]证明了有限CSL代数在零点处的范数连续的广义可导映射是广义导子。文献[8]证明了δ是零点可导映射当且仅当有一个导子τ:T→T使得δ(A)=τ(A)+δ(I)A。李红霞和段樱桃[9]研究了标准算子代数上在零点处的可导映射与可导映射之间的关系,并得出了在零点处的可导映射是广义内导子。文献[10]证明了上三角矩阵代数上的零点Jordan可导映射是导子。近年来,对于关联代数上映射的研究也引起了诸多学者的关注[11-14]。肖占魁[15]利用代数组合的方法刻画了关联代数上Jodan导子,并证明了关联代数上的每一个Jordan导子是导子。张弦[16]证明了关联代数上的Lie导子都是标准的。随后文献[17]把以上两个文献的结论推广到Lie三重导子上。受以上研究的启发,本文利用代数组合的方法刻画了关联代数上的零点可导映射。

1 预备知识

定义1设A是一个结合代数,φ:A→A是一个线性映射,如果对任意a,b∈A且ab=0,有φ(ab)=φ(a)b+aφ(b),则称φ是零点可导映射。

定义2设A是一个结合代数,φ:A→A是一个线性映射,如果对任意a,b∈A且ab=0,有φ(ab+ba)=φ(a)b+aφ(b)+φ(b)a+bφ(a),则称φ是零点Jordan可导映射。

定义3设R是含单位元的交换环,(X,≤)是一个局部有限的预序集,在R上定义关于X的关联代数I(X,R):

I(X,R)

={f:X×X→R|f(x,y)=0,若x≤y不成立}

代数运算如下:

(f+g)(x,y)=f(x,y)+g(x,y)

(rf)(x,y)=rf(x,y)

∀f,g∈I(X,R),r∈R,x,y,z∈X。其中乘积fg称为卷积。

关联代数I(X,R)的单位元定义为δ(x,y)=δxy,x≤y,其中δxy∈{0,1}是Kronecker符号。对于任意的x,y∈X满足x≤y,定义基元exy(u,v)=1,若(u,v)=(x,y),其他情形为零。由卷积的定义可知exyeuv=δyuexv,关联代数上的一组线性基记为B:{exy|x≤y}。

定义4设偏序集X中的序列为x=x0,x1,x2,…,xn=y,则对于任意的i=0,1,…,n-1满足xi≤xi+1或xi≥xi+1,则在偏序集X中的元素x,y是连通的。

2 主要定理及证明

引理1[16]假设φ:I(X,R)→I(X,R)是一个R-线性映射,对任意i,j∈X且i≤j,记

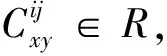
下面利用代数组合的方法给出了关联代数上的零点可导映射的表达形式和满足的系数关系式。

定理1设X是有限连通的预序集,φ是关联代数I(X,R)上的零点可导映射,则

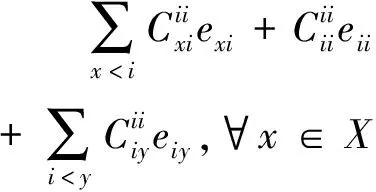
(1)

(2)

证明由零点可导映射的定义以及卷积的定义,对eii,eyy∈I(X,R),若y≠i,有eiieyy=δiyeiy=0,则

0=φ(eiieyy)=φ(eii)eyy+eiiφ(eyy)

(3)

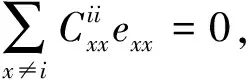
(4)

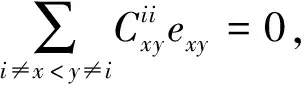
(5)

综合(4)(5)可得

故(1)式得证。

由等式(1)知

对eii,eij∈I(X,R),有eijeii=δjieii=0,结合等式(1)则

0=φ(eijeii)=φ(eij)eii+eijφ(eii)

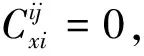
(6)

对ejj,eij∈I(X,R),有ejjeij=δjiejj=0,则

0=φ(ejjeij)=φ(ejj)eij+ejjφ(eij)

(7)

对eii,eij∈I(X,R),有eijeii=eiieijeii=0,则

0=φ(eijeii)=φ(eiieijeii)

=eiiφ(eij)eii+eijφ(eii)

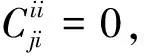
(8)

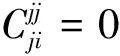
(9)

类似地,对exx,eij∈I(X,R),若x≠i,j,有exxeij=exxeijexx=0,则

0=φ(exxeij)=φ(exxeijexx)

(10)

(11)

综合(6)(7)(11)可得

故(2)式得证。

(12)

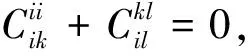
(13)

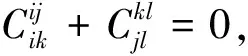
(14)

证明对任意的i≤j,k≤l,有eijekl=δjkeil,由零点可导映射的定义以及卷积定义,下面分三种情形讨论。

情形1若i=j且k=l

情形1.1当i≠k时,有eiiekk=δikeik=0,结合等式(1)则

0=φ(eiiekk)=φ(eii)ekk+eiiφ(ekk)

当i=k时,由于eiiekk=δikeik≠0,不是零点,故不满足。

情形2若i=j且k≠l(与若i≠j且k=l的情形对称)

情形2.1当i≠k时,有eiiekl=δikeil=0,结合等式(1)(2)则

0=φ(eiiekl)=φ(eii)ekl+eiiφ(ekl)

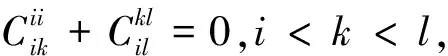
当i=k时,由于eilekl=δikeil≠0,不是零点,故不满足。

情形3若i≠j且k≠l

情形3.1当j≠k时,有eijekl=δjkeil=0,结合等式(2)则

0=φ(eijekl)=φ(eij)ekl+eijφ(ekl)

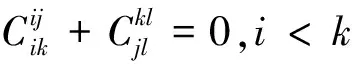
当j=k时,有eijekl≠0,不是零点,故不满足。证毕。

引理2[16]假设φ:I(X,R)→I(X,R)是一个R-线性映射,对任意i,j∈X且i≤j,记

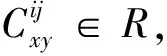
下面利用代数组合的方法给出了关联代数上的零点Jordan可导映射的表达形式和满足的系数关系式。

定理3设X是有限连通的预序集,φ是关联代数I(X,R)上的零点Jordan可导映射,则

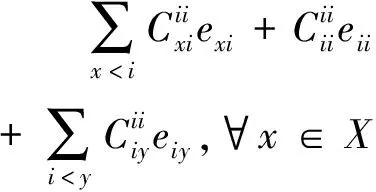
(15)

(16)

证明由零点Jordan可导映射的定义以及卷积的定义,对eii,exx∈I(X,R),若x≠i,有eiiexx=δixeix=0,则

0=φ(eiiexx+exxeii)

=φ(eii)exx+eiiφ(exx)+φ(exx)eii

+exxφ(eii)

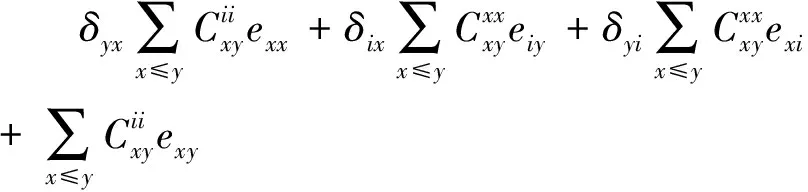
(17)

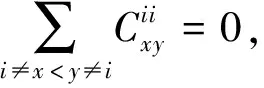
(18)

综合(17)(18)可得

故(15)式得证。

对eij,eii∈I(X,R),有eijeii=δjieii=0,结合等式(15)则

φ(eij)=φ(eijeii+eiieij)

=φ(eij)eii+eijφ(eii)+φ(eii)eij

+eiiφ(eij)

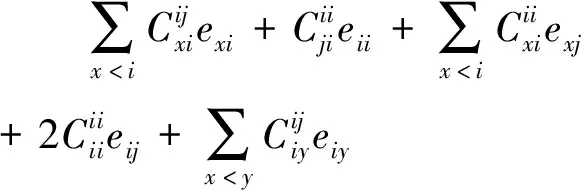
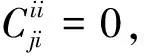
(19)

对ejj,eij∈I(X,R),有ejjeij=δjiejj=0,结合等式(15)则

φ(eij)=φ(ejjeij+eijejj)

=φ(ejj)eij+ejjφ(eij)+φ(eij)ejj

+eijφ(ejj)

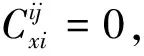
(20)

对于exx,eij∈I(X,R),当x≠i,j,有exxeij=exxeijexx=0,则

0=φ(exxeijexx+exxeijexx)

(21)

类似地,对eii,eij∈I(X,R),有eiieij=eiieijeii=0,则

0=φ(eiieijeii+eiieijeii)

=2eiiφ(eij)eii+2eijφ(eii)

(22)

类似地,对ejj,eij∈I(X,R),有ejjeij=ejjeijejj=0,则

0=φ(ejjeijejj+ejjeijejj)

=2φ(ejj)eij+2ejjφ(eij)ejj

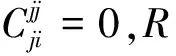
(23)

结合(21)(22)(23)可得

(24)

综合等式(19)(20)(24)可得

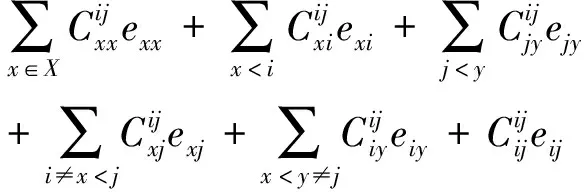
故(16)式得证。

(25)

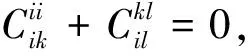
(26)

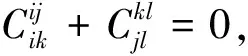
(27)

证明对任意的i≤j,k≤l,有eijekl+ekleij=δjkeil+δliekj,由零点Jordan可导映射的定义以及卷积定义,下面分三种情形讨论。

情形1若i=j且k=l

情形1.1当i≠k时,对eii,ekk∈I(X,R),有eiiekk=δikeik=0,则

0=φ(eiiekk+ekkeii)

=φ(eii)ekk+eiiφ(ekk)

+φ(ekk)eii+ekkφ(eii)

当i=k时,eiiekk=δikeik≠0,不是零点,故不满足。

情形2若i=j且k≠l(与若i≠j且k=l的情形对称)

情形2.1当i≠k和i≠l时,对eii,ekl∈I(X,R),有eiiekl=δikeil=0,则

0=φ(eiiekl+ekleii)

=φ(eii)ekl+eiiφ(ekl)

+φ(ekl)eii+eklφ(eii)

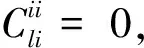
情形2.2当i≠k和i=l时,对eii,ekl∈I(X,R),有eiiekl=δikeil=0,则

φ(eki)=φ(eiieki+ekieii)

=φ(eii)ekl+eiiφ(eki)

+φ(eii)eki+eiiφ(eki)

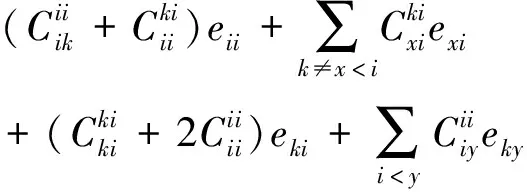
当i=k和i=l时以及i=k和i≠l时,不是零点,都不满足。

情形3若i≠j且k≠l

情形3.1当j≠k且l≠i,对eij,ekl∈I(X,R),有eijekl=δjkeil=0,则

0=φ(eijekl+ekleij)

=φ(eij)ekl+eijφ(ekl)

+φ(ekl)eij+eklφ(eij)

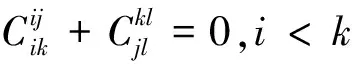
情形3.2当j≠k和l=i时,对eij,ekl∈I(X,R),有eijeki=δjkeii=0,则

φ(ekj)=φ(eijeki+ekieij)

=φ(eij)eki+eijφ(eki)

+φ(eki)eij+ekiφ(eij)

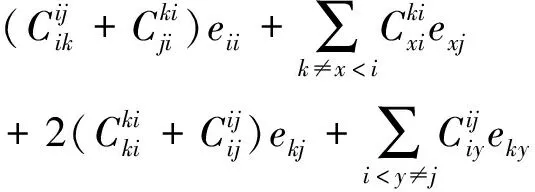
当j=k和l≠i以及j=k和l=i时,不是零点,都不满足,证毕。

定理5设X是有限连通的预序集,R是含有单位元的2-扭自由的交换环,则关联代数I(X,R)上的每一个零点Jordan可导映射是零点可导映射。

证明设φ:I(X,R)→I(X,R)是零点可导映射,由定理1和定理2可得

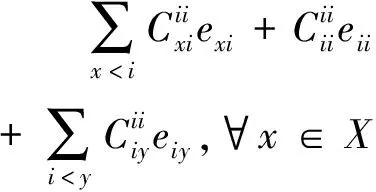
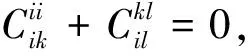
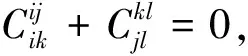
在R上定义线性映射φ

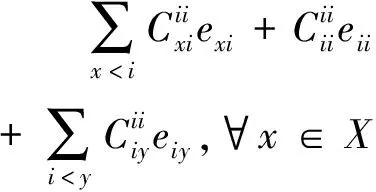
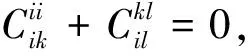
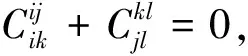
由定理3和定理4可知φ是零点Jordan可导映射且线性映射:θ=φ-φ满足

θ(eii)=φ(eii)-φ(eii)=0

θ(eij)=φ(eij)-φ(eij)=0

故得证。