Broadband multi-channel quantum noise suppression and phase-sensitive modulation based on entangled beam

Ke Di(邸克), Shuai Tan(谈帅), Anyu Cheng(程安宇), Yu Liu(刘宇), and Jiajia Du(杜佳佳)

Chongqing University of Post and Telecommunications,Chongqing 400065,China

Keywords: quantum entanglement,broadband quantum interference,phase-sensitive modulation

1.Introduction

Entangled state optical fields are widely studied since they are an essential resource in next-generation quantum communication technologies.They have been applied in quantum secret key distribution,[1,2]quantum secret key sharing,[3,4]quantum teleportation.[5,6]An entangled state light field can exist in both discrete variable and continuous variable forms.Discrete variables of entangled photon pair have excellent fidelity.[7,8]However, an entangled light field in continuous variable has many advantageous such as superior broadband, excellent stabilization, and high operating efficiency.[9,10]The continuous variable of quantum entangled beam at 1550 nm communication band wavelength was produced by Fenget al.[11]Wenet al.proposed a scheme for tunable three-mode entanglement of continuous variable.[12]Two-mode entangled-state beams are applied within miniature waveguide circuits,which is a crucial step towards fully integrated quantum information.[13]The transmission threshold of quantum repeater can be enhanced by manipulating a continuous variable entangled state of optical fields.[14]

Entangled light has important applications in the field of quantum communication.Considering the decay of light beams during propagation, it has been introduced into optical parametric amplification systems to study relevant properties.Maet al.investigated mode splitting within the transmission spectrum of a phase-sensitive optical parametric amplifier in a single optical parametric amplifier(OPA)system.[15]Reflected field quantum fluctuation interference was demonstrated theoretically in a single OPA system by Agarwal.[16]Later, Chenet al.applied entangled light to a single OPA system and produced electromagnetically induced transparentlike(EIT-like)line shape phenomena at theΔ=0 MHz.[17]All of the above studies were in single OPA systems.The scheme of Chenet al.is more similar to ours.However,their scheme only produces quantum coherence effects atΔ=0 MHz and has a narrow window for such coherence effects.Our scheme is achieved in a coupled resonant cavity system.It turns out that quantum noise suppression windows can be generated at multiple detuning frequencies.As the coupling strength of the model is increased, the width of the quantum noise suppression windows can be significantly broadened.Diet al.experimentally achieved induced transparency in coupled resonant systems.[18]However,a squeezed field was injected into their system without nonlinear crystal.Hence the parametric downconversion cannot occur.As the results in this study,it can be seen that nonlinear crystals play an important role in broadening the quantum noise suppression windows.

In this paper, we provide a multi-channel quantum entanglement scheme in a coupling resonant system which consists of a periodically poled potassium titanyl phosphate(PPKTP) crystal and two cavities.The PPKTP crystal is driven by pumping light and embedded in cavity C2.We carefully investigate the multi-channel quantum interference and entanglement properties of the system with phase-sensitive modulation.A detailed comparison between the OPA resonant cavity and the coupling resonant cavity is also presented.Our results show that the coupling resonant system generates the entanglement properties of multi-channel simultaneously, and the strong coupling resonant cavity can broaden the bandwidth of each channel by 2-3.5 times.The nonlinear crystal enhances the entanglement strength of the output field as the entangled light is injected into the system.Furthermore, quantum noise suppression at quadrature amplitude is achieved with phase-sensitive modulation, which can be applied to improve measurement accuracy.Each broadband quantum interference channel presents an EIT-like line shape, which is expected to be applied in quantum information processing[19]and quantum memory to improve the transmission stability of wave packet.[20-22]

2.Theoretical model

Figure 1 schematically shows a coupling resonant system.The coupling resonant cavity consists of two flat-concave mirrors Mfront, Mbac, and a plane mirror Mmid.Cavities C1and C2are connected by a plane mirror Mmid.The coupling coefficient depends on the reflectivity rate of the middle cavity mirror.A nonlinear crystal is placed at the center of cavity C2.Cavity C2in Fig.1(a) consists of a flat-concave mirror Mbac, a plane mirror Mmid, and a nonlinear crystal (PPKTP),which form an OPA system.The threshold limit is defined asHereβis the amplitude of the pumping light, andgis the nonlinear susceptibility.The function of the scaled pumping amplitude is defined asThe OPA system we studied worksEth＜1 below the threshold.The annihilation of the pumping photon provides energy to cavity C2and generates a low-frequency signal photon and an idle photon.As a result, the number of signal photons increases,which leads to an optical amplification effect.

Fig.1.Scheme diagram of coupling resonant system.(a)The coupling resonant cavity model.Optical cavity C1 and optical cavity C2 are coupling by a middle mirror Mmid;r1(t1),r2(t2)and r3(t3)denote the reflection(transmission)coefficients for cavity mirrors Mfront,Mmid,and Mbac,respectively.Signal light ain1 and idle light ain2 are light fields with entanglement properties.(b)An equivalent model diagram based on the input-output relationship and the strength of the optical field at different positions in the optical cavity C1. R(T)is the total reflectance(transmittance)of cavity C1.(c)The diagram of simplified coupling resonant system model.

We adopt a semi-classical approach to superimpose cavity C1as shown in Fig.1(b).[23,24]The reflection coefficient of the whole cavity C1can be obtained from the relationship between the input and output of the light field in a single optical cavity.The cavity C1is physically equivalent to the front cavity mirror MF, which eventually enables the coupled resonant cavity model to be simplified to a single cavity system as shown in Fig.1(c).The coupling strength of the two cavities (C1and C2) can be effectively controlled by adjusting the transmission coefficient of the intermediate cavity mirror Mmid.Therefore, the superimposed system model (Fig.1(c))also has the characteristics of a coupled resonant cavity.The Hamiltonian of the system(Fig.1(c))can be written as[25-27]

The coupling resonant cavity system model can produce multi-channel quantum interference effects compared to single cavity (without middle mirror Mmid).The reflection coefficientRof the overall cavity C1can be obtained according to the input-output relationship and the strength of the optical field at different positions[24]

whereLis the length of cavity C1,ωjis the optical field frequency,γcrepresents other decay effects in cavity C1.

The Langevin equation for different modes can be obtained by the equation ˙ˆOj=(1/iħ)[ˆOj,H0]-γjˆOj+ ˆOinj.[28]Consider the dissipation and input noise of each mode, the Langevin equations of motion for our system can be written as[29,30]

By linearizing Eq.(3),we take the Langevin equations of motion into the Eq.(4)and make the Fourier transform read

where

Similarly, the quantum correlation spectrum of quadrature phase is obtained as

Equations(9a)-(9d)get plus signs wheni=c,and they get minus signs wheni=d.The parametersare given by

Equations(10a)-(10d)get plus signs wheni=d,and they get minus signs wheni=c.

Subsequently,the final quantum noise correlated variance fluctuation equation of quadrature amplitude for signal light and idle frequency light is obtained as follows:[15,33]

Similarly,the noise covariance of quadrature phase is obtained to be

Equations (13a)-(13d) get plus signs wheni=c, and they get minus signs wheni=d.The parametersare given as

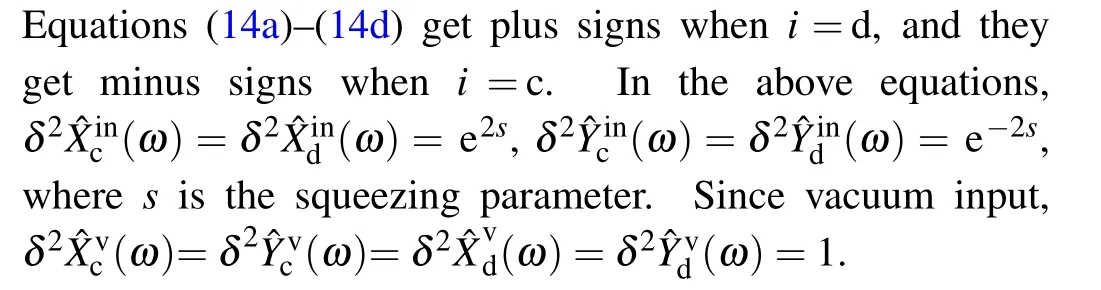
As shown in the following equation, Duan and Simon proposed a non-separability criterion for two-mode measurable squeeze variance.[34,35]Specifically,a sufficient condition for entanglement is that the correlated quadrature components satisfy the inequality

3.Discussion

3.1.A weak coupling resonant cavity with entangled state

Figure 2 shows multi-channel quantum interference phenomenon and quantum entanglement results with the pumping powerEth=0.2βth(Eth=0.5βth).

Fig.2.Quantum covariance function in weak coupling resonant cavity.The green curves denote the shot-noise limit (SNL).The intensity of the pumping power at 0.2βth(0.5βth)is blue(red).[(a),(b)]The quadrature amplitude(a)and quadrature phase distribution function(b)of the entangled beam pair in a single cavity.[(c),(d)]Quadrature amplitude ˆXc (c)and phase ˆYc (d)when the pumping light phase is θ =0.[(e),(f)]Quadrature amplitude ˆXd (e)and phase ˆYd (f)when the pumping light phase is θ =π.

Firstly,we focus on the single cavity model which can be achieved by removing the cavity mirror Mmidof the coupling resonant system.The transmission parameters of the front mirror and back mirror aret1=0.0016 andt3=0.00005.[17,36]A continuous variable entangled beam injects into the single cavity,and the quantum noise correlation curves are shown in Figs.2(a) and 2(b).Figure 2(a) provides a curve of quantum noise fluctuations at quadrature amplitude.Due to the nondegenerate OPA, the signal field and idle field interactions at theΔ=0 MHz,the curve is amplified and two weak squeezed states appear at two sidebands.The overall curve shows an EIT-like line shape.Figure 2(b)shows the quantum fluctuation noise curve at the quadrature phase.Due to the Heisenberg uncertainty principle,the quantum noise fluctuation curve at the quadrature phase shows a squeezed state.The degree of noise suppression is up to 6.55 dB at the quadrature phase.

Next, we consider the weak coupling resonant system with three mirrors Mfront,Mmidand Mbac.Coupling strength of cavities C1and C2depends on the transmittance of the middle mirror Mmid.According to the accessible parameters in experiments by Diet al.,[18]the parameters of the mirrors in the coupling resonant cavity are adjusted as follows:t1=0.05,t2=0.014,t3=0.002.In the coupling resonant system, the quantum interference effect is significantly enhanced compared to the single cavity system.The quantum noise fluctuation curves of the pumping phase atθ=0 are shown in Figs.2(c) and 2(d).Due to the coupling of cavities C1and C2, multi-channel quantum interference phenomena can be observed from Figs.2(c) and 2(d).They are simultaneously distributed at different detuning frequenciesΔ=0 MHz andΔ=±3.1 MHz, respectively.These EIT-like multi-channel quantum interference effects are more sensitive to pumping light.Strong pumping power can effectively enhance the quantum interference phenomenon in each channel.Meanwhile,we adjust the phaseθfrom 0 toπof the pumping light to achieve phase-sensitive modulation.As shown in Fig.2(e),the peaks at different detuning frequencies switch from positive to negative values.In contrast, the peaks at different detuning frequencies switch from negative value to positive value in Fig.2(f).Phase-sensitive modulation achieves multichannel quantum noise suppression of quadrature amplitude while sacrificing bandwidth compared to Figs.2(c) and 2(d).However,the bandwidth of the EIT-like quantum interference channel at theΔ=0 MHz detuning is obviously broadened in comparison to the single cavity system.

3.2.A strong coupling resonant cavity with entangled state

Figure 3 shows the quantum interference properties of the entangled light in the strong coupling resonant system.The coupling strength depends on the transmittancet2of the middle mirror Mmid.We change the transmittancet2=0.15 of the middle mirror Mmidand the other parameters are the same as those of the weak coupling resonant cavity.Owing to the increasing coupling strength between cavities C1and C2, all the quantum interference channels are effectively broadened,compared to weak coupling resonator system.

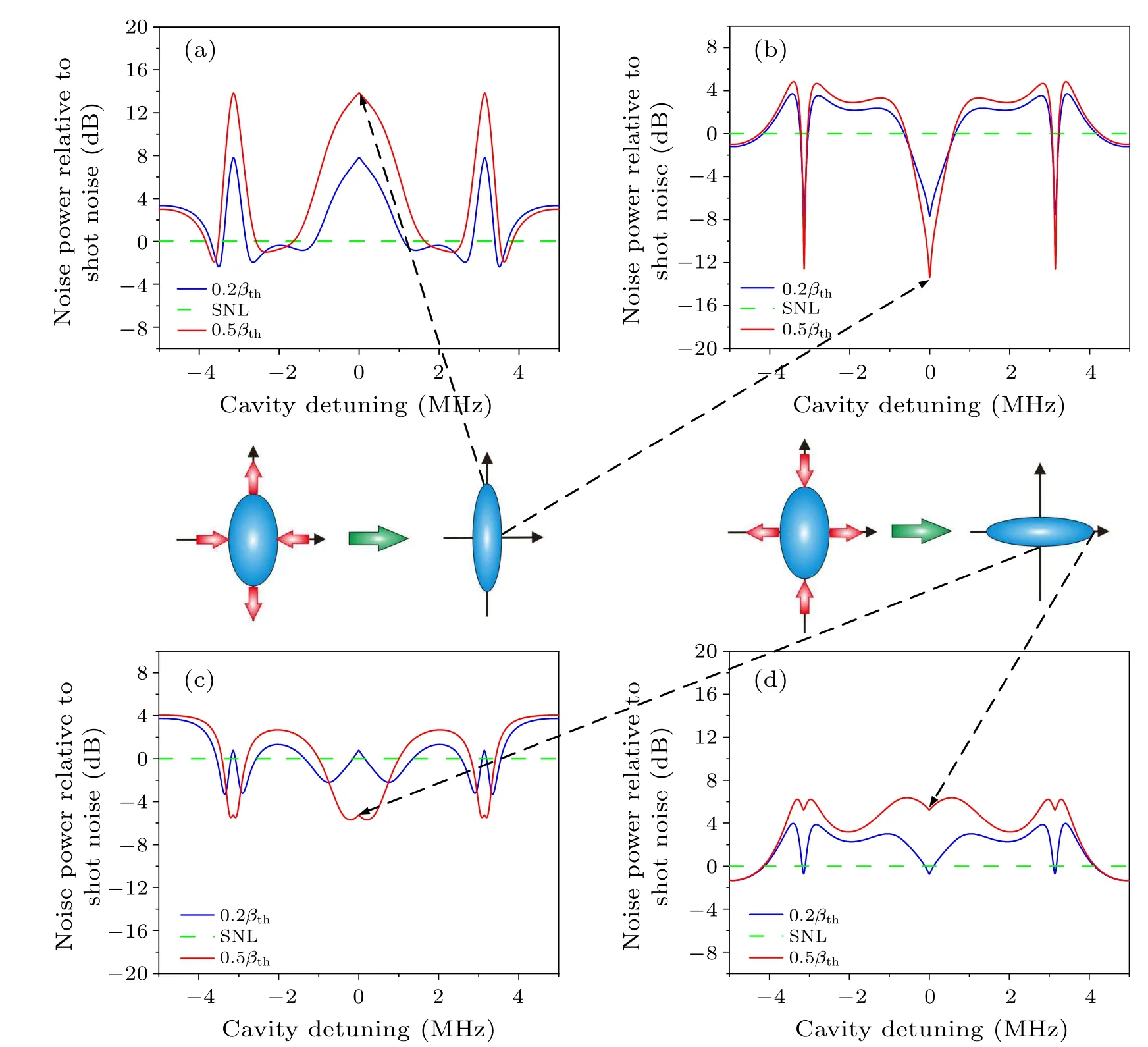
Fig.3.Quantum covariance function in strong coupling resonant cavity.[(a),(b)]Quadrature amplitude ˆXc and phase ˆYc with θ =0.[(c), (d)] Quadrature amplitude ˆXd and phase ˆYd with θ =π.The transmittance of the middle mirror Mmid is t2 =0.15.Other parameters are the same as those of the weak coupling resonant system.

Quantum interference channel is broadened 2.17 times at theΔ= 0 MHz compared to single cavity resonant cavity.Meanwhile, the quantum interference channel of the strong coupling resonant cavity at theΔ=0 MHz(Δ=±3.1 MHz)is broadened up to 1.27 (3.53) times compared to that of the weak coupling resonant system.In addition, it can also be achieved to broaden the EIT-like quantum interference windows by appropriately increasing the pumping optical power.Wider EIT-like window can be better matched to the detection pulse and a larger group delay can be obtained.[37]The generation of multiple broadband EIT-like quantum interference channels facilitates improving the efficiency of wave packet propagation and reducing the distortion rate during acquisition of quantum information.[38-40]

3.3.Analysis of entanglement properties in different systems

Figure 4 show the entanglement properties of the single cavity and coupling resonant system.From Fig.4(a), we observe that the entanglement strength of the output field is highest atΔ=0 MHz and two weak entangled state appear symmetrically on both sides of theΔ=0 MHz.

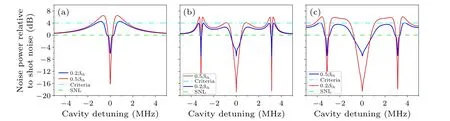
Fig.4.The entanglement results of(a)signal light and idle light in single cavity,(b)weak coupling resonant system,and(c)strong coupling resonant system.The cyan curves denote non-separability criterion.Other parameters are the same as those of the weak coupling resonant system.

In Fig.4(b),it can be clearly seen that entanglement exists at the central frequencies of EIT-like multiple quantum interference channels.The entanglement strength is up to 19.8 dB when the pumping light power is 0.5βth.A strong coupling resonant system can be realized whent2=0.15.The entanglement properties of each quantum interference channel in the strong coupling resonant system are shown in Fig.4(c).A strong coupling resonant cavity does not enhance the entanglement strength compared to Fig.4(b).However, the strong coupling resonance system can effectively broaden the quantum interference channel, the range of entanglement is also broadened.The phenomenon of multiple EIT-like quantum interference entanglement channels appearing simultaneously is beneficial to improve the efficiency of quantum information transfer.It has potential applications in the fields of quantum communication[41-43]and quantum storage,[44]etc.

4.Conclusion

In summary, multi-channel quantum noise suppression,phase-sensitive modulation and entanglement properties generated by entangled light are systematically analyzed in a coupling resonant system with different coupling strengths.Compared to the single cavity(weak coupling resonant cavity)system, the bandwidth is broadened by 2.17 (3.53) times withΔ=0 MHz (Δ=±3.1 MHz) in a strong coupling resonant system.The output field presents entanglement properties at multiple frequencies,which can effectively enhance the information carrying capacity of quantum communication systems.Our results have potential applications in fields of quantum information processing,[40,45]multi-channel EIT memory,[46]and quantum precision measurement,[47-49]etc.

Acknowledgments

Project supported by National Natural Science Foundation of China (Grant Nos.11704053 and 52175531) and the Science and Technology Research Program of Chongqing Municipal Education Commission(Grant No.KJQN201800629).