High efficient Raman sideband cooling and strong three-body recombination of atoms
2023-11-02YuqingLi李玉清ZhennanLiu刘震南YunfeiWang王云飞JizhouWu武寄洲WenliangLiu刘文良YongmingFu付永明PengLi李鹏JieMa马杰LiantuanXiao肖连团andSuotangJia贾锁堂
Yuqing Li(李玉清), Zhennan Liu(刘震南), Yunfei Wang(王云飞), Jizhou Wu(武寄洲),†,Wenliang Liu(刘文良), Yongming Fu(付永明), Peng Li(李鹏),Jie Ma(马杰), Liantuan Xiao(肖连团), and Suotang Jia(贾锁堂)
1State Key Laboratory of Quantum Optics and Quantum Optics Devices,Institute of Laser Spectroscopy,College of Physics and Electronics Engineering,Shanxi University,Taiyuan 030006,China
2Collaborative Innovation Center of Extreme Optics,Shanxi University,Taiyuan 030006,China
Keywords: matter wave,atom cooling methods,ultracold gases
1.Introduction
Laser cooling and trapping techniques enable the preparation and application of atomic ensembles at ultracold temperatures, where many quantum effects will dominate.[1-7]As a kind of sub-Doppler cooling, gray molasses has been demonstrated as a powerful tool to cool the atomic sample to a lower temperature for6Li,[8-10]7Li,[11]23Na,[12,13]39K,[14,15]40K,[9,16]41K,[17]87Rb[18]and133Cs atoms[19]than the general optical molasses cooling.In a different approach, threedimensional degenerated Raman sideband cooling(3D dRSC)was earlier used to obtain sub-µK temperature in the pioneering works on Cs atoms.[20,21]3D dRSC is also indispensable for Cs atoms to achieve their atomic Bose-Einstein condensate.[22-25]Quite recently,3D dRSC has been used for39K atoms and produces a lower temperature ofT=1.3 µK compared to the result from the gray molasses cooling.[26]For the87Rb and133Cs atoms trapped in a 2D optical lattice operating at the wavelength ofλ=1064 nm,dRCS enables the production of quantum gases by the direct laser cooling.[27,28]
Since dRSC is used to cool the atomic sample to a low temperature around 1 µK, a large volume optical dipole trap(ODT)with the shallow trapping potential is beneficial to enhance the number of atoms loaded into the ODT.[29-31]For the interacting ultracold Bose atoms in the ODT, of particular interest is the three-body recombination,in which two particles form a dimmer while interacting with a third particle.Understanding the three-body recombination has for a long time been important in the studies of both few- and manybody physics in ultracold atoms.[32]The universal scaling laws in the strongly correlated unitary Bose gases dominated by the three-body recombination have been explored experimentally and theoretically.[33-36]For the non-degenerated ultracold Bose atoms at the large scattering length,the three-body recombination induces the large atom loss and heating.[37-39]Thus, a highly efficient 3D dRSC is promised for the preparation of a large number of atoms in the optical dipole trap,and a comprehensive study of the three-body recombination is significant for understanding the unequilibrium process after loading of cooled atoms into the optical dipole trap.
In this work, we realize a highly efficient 3D dRSC for Cs atoms and obtain an ultracold temperature ofT~500 nK.The cold temperature is consistent with the theoretical estimation according to the calibrated energy spacing of neighboring vibrational levels in the lattice used in 3D dRSC.Combined with the optimized excessive levitation gradient,the cold temperature enables a large number of atoms to be loaded into the magnetically levitated ODT.The evolution of the number of atoms trapped in the ODT is measured at a large scattering length, and a strong three-body loss is observed.The threebody recombination coefficient is obtained by fitting the derived model to the data.In particular, the one-body loss due to the collisions of atoms with background gas becomes dominant after the large reduction of atomic density under the initial strong three-body loss.
2.Experimental setup and process
The experimental scheme of 3D dRCS is basically the same as the previous works on Cs atoms.[20,21,27,28]The main difference is the geometric configuration of the lasers constructing the lattice and the optical pumping laser.As shown in Fig.1,a stable 3D lattice is formed by using one retroreflected standing wave and two running waves.The standing wave has an angle of~77°with the vertical direction, and is perpendicular to another beam with an angle of~13°relative to the horizontal plane.The linear polarizations of the two running beams lie in a plane, which is formed by these two running beams.The two polarizations of the standing wave are rotated by±10°relative to the angular bisector of the two running beams.This special polarization configuration of four laser beams guarantees the maximum of the Raman coupling in 3D dRSC.The optical pump laser is calibrated to aσ+polarization and reflected by a mirror.The magnetic field is optimized to mainly parallel to the optical pump laser beam.
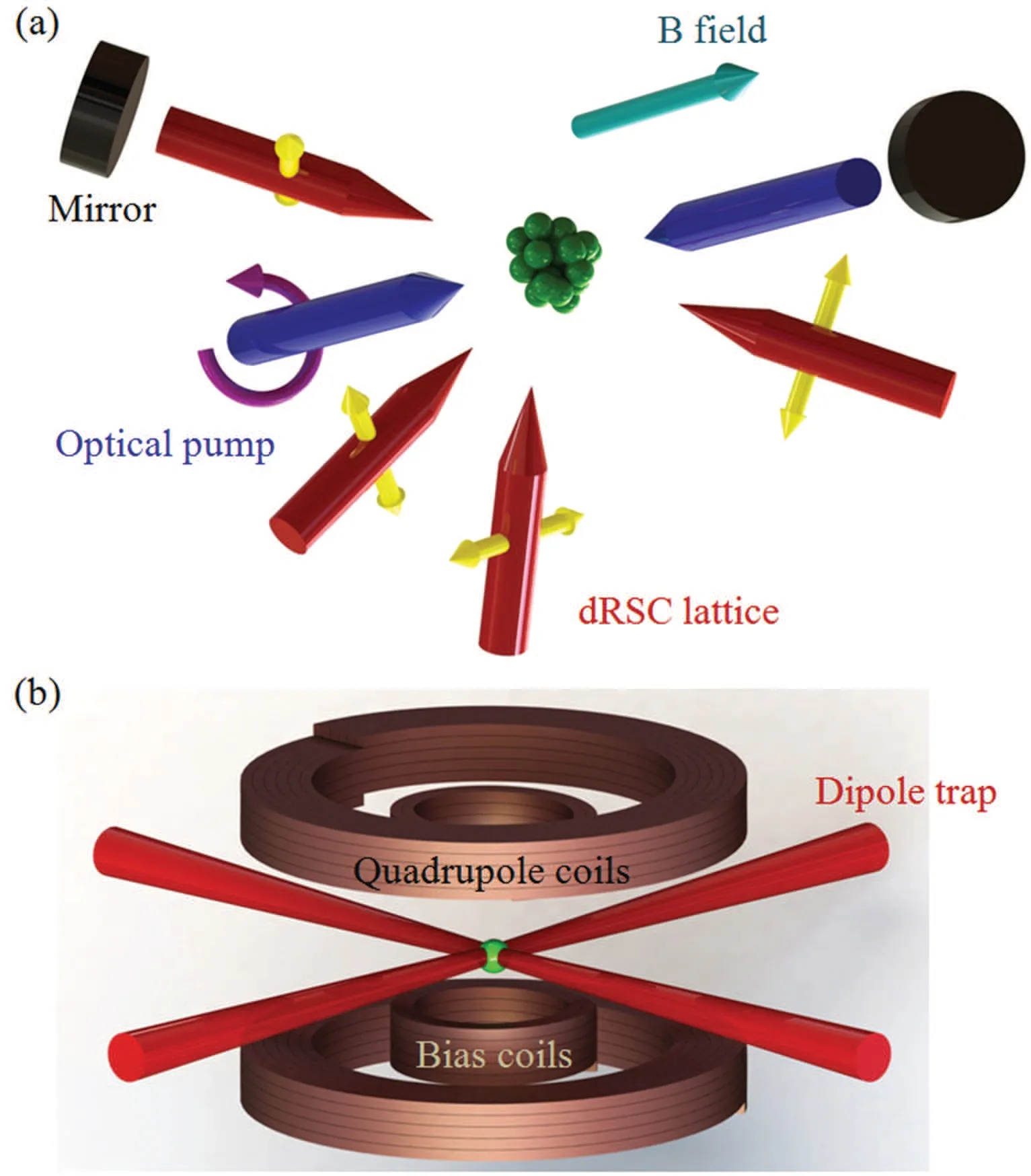
Fig.1.Experimental geometry and configuration of both lasers and magnetic coils for the 3D dRSC and the magnetic levitated loading of ODT.(a) The lattice (red inward arrows) consists of two running laser beams with the polarizations that lie in the plane determined by these two beams and the retro-reflected standing wave with the±10° polarizations(yellow arrows) relative to the angular bisector of the two running beams.The optical pump laser(blue arrows)has the σ+ polarization and reflected by a mirror.The direction of the combined magnetic field is mainly parallel with the optical pump laser beam.(b) The magnetically levitated ODT consists of a pair of quadrupole coils in anti-Helmholtz configuration, a pair of bias coils in Helmholtz configuration,and two horizontally crossing 1064-nm laser beams at an angle of ~90°.
The lattice lasers are derived from a power-amplified external-cavity diode laser(ECDL),which is operated without the frequency stabilization.The frequency is tuned to a red detuning ofΔl=-22 GHz from the 6S1/2,F=3→6P3/2,F'=4 transition of Cs atoms.The standing wave laser has the power of~46 mW,and the other two running lasers have the same power of~16.5 mW.A weak magnetic field,which is used to bring the vibrational sublevel|n〉in the|F=3,mF〉state to degeneracy with the vibrational sublevel|n-1〉in the|F=3,mF-1〉 state, is provided by the combined field of three pairs of compensation coils.This magnetic field is optimized by minimizing the atomic temperature and maximizing the number of atoms after 3D dRSC.The optical pumping laser with the power of~1.2 mW is from another ECDL,which provides the repumping laser in the magneto-optical trap (MOT), and is detuned by +10 MHz from the 6S1/2,F= 3→6P3/2,F'= 2 transition.An additional depumping laser is introduced to pump the atoms back to theF=3 ground state, since the excited atoms in 3D dRSC can decay to theF=4 ground state,in which the atoms can’t participate in the cooling process.Here the cooling laser in MOT is used for the depumping laser and is detuned by+10 MHz relative to the 6S1/2,F=4→6P3/2,F'=4 transition.
After 3D dRSC,we use a large-volume crossed ODT with the shallow potential of~kB×9 µK to capture more atoms,wherekBis the Boltzmann constant.The ODT consists of two horizontally crossing 1064-nm laser beams at an angle of~90°.These two beams have the same power of~2 W,and the beam waists arewx=310±12µm andwy=300±13µm.During the loading of ODT, the large gravity of Cs atom induces a big destructive potential in the vertical direction.[41]To compensate the gravity and form an effective trapping potential,a magnetic field gradient of∂B/∂z=31.3 G/cm needs to be applied for the Cs atoms in theF=3,mF=3 state to cancel the gravity completely, i.e.,whereµBis Bohr’s magneton,gF=-1/4 denotes the Land´eg-factor,andgis the gravitational acceleration.The magnetic field gradient is produced by a pair of quadrupole coils, as shown in Fig.1(b).
According to Maxwell’s equation of ∇·B= 0 and the cylindrical symmetry, the application of∂B/∂zleads to the horizontal magnetic field gradient of∂B/∂x=∂B/∂y=-1/2∂B/∂z, which causes the horizontal outward pointing force and leads to the anti-trapping potential in the horizontal direction.In order to eliminate the influence of the anti-trapping potential along the horizontal direction,we use a vertical bias fieldB0,which is produced by another pair of Helmholtz coils shown in Fig.1(b),to reduce the outward force.The combined field leads to a horizontal trapping frequency
whereε=0.0303 cm-2denotes the departure of the actual geometry of magnetic coils from the Helmholtz configuration.
3.Results
3.1.The 3D degenerated Raman sideband cooling
Cs atoms are slowed down by a Zeeman slower and then collected by a MOT with up to~5×108atoms.Through the compressed MOT and optical molasses cooling, we have 6×107atoms with the temperature of~8 µK.For a lower temperature,we use 3D dRSC to further cool and polarize the atoms in theF=3,mF=3 state.The lattice in 3D dRSC is adiabatically switched on before the end of optical molasses for 0.5 ms, and the depumping laser is simultaneously switched on to keep the atoms populating in theF=3 state.The magnetic fields produced by three pairs of compensation coils are adjusted to the optimized values for 2.5 ms previous to the switching of the optical pump laser, because the compensation coils have a 1.5-ms delay.During the cooling process, the atoms are transferred from the|6S1/2,F=3,mF,n〉state into|6S1/2,F=3,mF-1,n-1〉 by a two-photon Raman process, and then the atoms are excited by theσ+optical pumping laser to the|6P3/2,F'=2,mF,n-1〉state.In the lamb-Dicke regime ofwhereEris the recoil energy of photon andωis the vibrational frequency of the lattice in 3D dRSC,the vibrational quantum number is conserved in the spontaneous decay from the excited|6P3/2,F'=2,mF,n-1〉state.The cooling enables that the atoms finally populate in the|6S1/2,F=3,mF=2,n=0〉state,which is a dark state for theσ+pumping light with the 6S1/2,F=3→6P3/2,F'=2 transition.To transfer atoms to the|6S1/2,F=3,mF=3,n=0〉state, the direction of the magnetic field is slightly tilted relative to the optical pumping beam for a weaklyπ-polarized component.
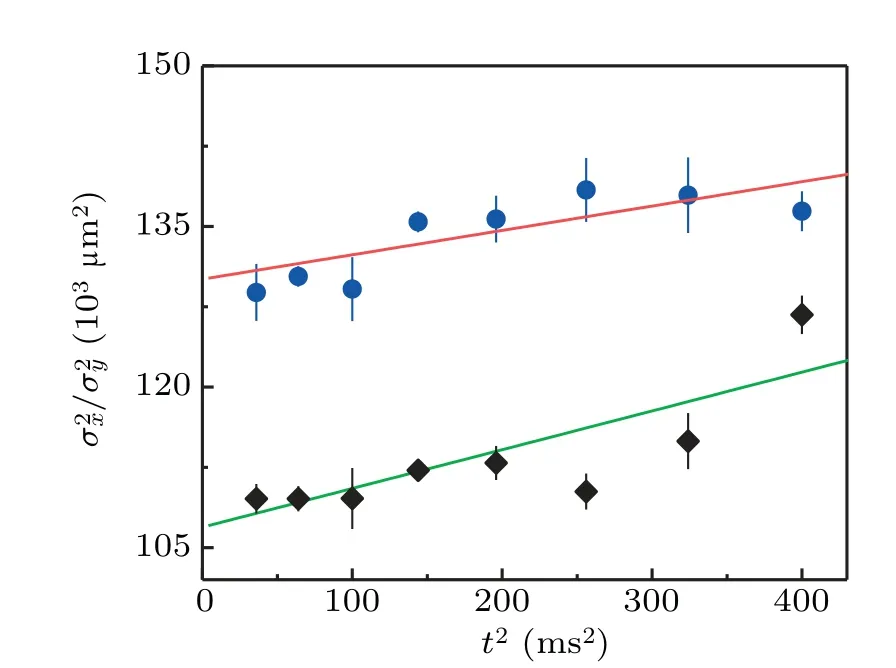
Fig.2.The square of the measured 1/e width of atomic cloud σ2x (blue circles) and σ2y (black diamonds) as a function of the square of flight time t2.The 1/e widths σx and σy are obtained through the atomic column density distribution along x and y directions,respectively.The temperature of atoms is given by using Eq.(2) to fit the data, and the red and green lines are the corresponding linear fittings.
After the 20-ms dRSC, the optical pumping laser and depumping laser are switched off,and then the lattice laser is adiabatically switched off.The number of atoms is measured asN=5×107by the absorption image.The atomic temperature is determined by fitting the linear dependence ofσ2i,tont2
whereσi,tis the 1/e width of the atomic cloud with subscriptibeing thexorydirection at the flight timet.[40]The fitted temperature isTx=360±120 nK andTy=580±160 nK,and the corresponding effective temperature is about 480 nK.
We precisely diagnose the magnetic field used in 3D dRSC by the microwave spectroscopy and estimate the atomic population in theF= 3,mF= 3 state.Here a 1-ms microwave pulse is used to pump the atoms in the 6S1/2,F=3 to the 6S1/2,F=4 state, and then the probe laser with the 6S1/2,F= 4→6P3/2,F'= 5 transition is used in the absorption image.Figure 3 shows the dependence of the number of atoms on the frequency of the microwave pulse.In Fig.3, we find five main peaks and they correspond to the transitions ofF= 3,mF= 3→F'= 4,m'F= 2, 3, 4 andF=3,mF=2→F'=4,m'F=1, 2, 3, where theF=3,mF=3→F'=4,m'F=2 transition has the same frequency with theF=3,mF=2→F'=4,m'F=3 transition.Any two adjacent peaks have the same energy spacing, which can be calculated by the Zeeman splitting under an external magnetic field.The transitional energy is given by
whereI= 7/2 is the nuclear spin of Cs atoms,EH=h×9192.63177 MHz is the hyperfine splitting of the ground state,gI=-3.98854×10-4is the nuclear Land´eg-factor,gJ=2.00254 is the fine structure Land´eg-factor in the 6S1/2ground state,andx=(gJ-gIµBB)/EH.[42]Based on Eq.(3),we calculate the splitting of the Zeeman sublevels induced by an external magnetic field, the effective magnetic field in 3D dRSC is derived for 108 mG.Thus the vibrational frequency of the lattice is determined asω=2π×50 kHz according to¯hω=ΔmFµBgFwith ΔmF=1.
In Fig.3, the population of atoms in the different Zeeman sublevels indicates that most of the atoms populate in theF=3,mF=3 state, and the other atoms mainly populate in theF=3,mF=2 state.The number of atoms populating in theF= 3,mF= 3 state is directly estimated asN ≥3.5×107by referring to the number of atoms detected with theF=3,mF=3→F'=4,m'F=3 microwave transition.The energy spacing between the two adjacent vibrational levels in the lattice of 3D dRSC defines the lowest temperature ofT=300 nK,but the obtained effective temperature ofT~480 nK is higher than the prediction.This may be attributed to the slight heating in the optical pumping process and the scattering of the photons from the lattice in 3D dRSC.The low temperature prevents the inelastic endothermic collisions of the Cs atoms in theF=3,mF=3 state and will improve the efficiency of loading the cooled atoms into the magnetically levitated ODT.

Fig.3.The number of atoms detected by using a microwave pulse instead of the repumping laser in absorption image as a function of microwave frequency.The peaks represent that the atoms in the sublevels of F =3, mF =1,2,3 are transferred to the sublevels of F =4,m'F =1,2,3,4 according to the selection rule of ΔmF =0,±1.Dots are from the experimental measurement, and the lines connecting the dots are used to guide the eyes.
3.2.Magnetically levitated optical dipole trap
During the loading of ODT, the magnetic field gradient should be switched on quickly for the formation of an effective trapping potential in the vertical direction.In our experiment,however,the eddy currents in the metal vacuum chamber and other stainless steel flanges limit the rapid variation of magnetic field gradient.When the magnetic force is increasing but has not yet compensated for the gravity completely,the remaining gravitational force always accelerates the atoms and hence leads to the heating of the atomic sample.Thus,to suppress the heating,an excessive levitation gradient of∂B/∂z >31.3 G/cm is used to reduce the velocity obtained by the atoms in the loading process of ODT.When the magnetic field gradient reaches∂B/∂z=31.3 G/cm,the atoms have the maximum downward velocity.With the continuous increase of∂B/∂z,an excessively magnetic force can reduce the downward velocity of atoms.The value of the excessive levitation gradient is optimized experimentally for a fixed duration of 4 ms.As shown in Fig.4(a), the number of atoms trapped in the ODT first increases and then decreases with the excessive levitation gradient, and an optimized value of∂B/∂z=40.5 G/cm is used to maximize the loading of atoms from 3D dRSC into the ODT.
The timing diagram for the magnetically levitated loading of ODT is summarized in Fig.4(a).When the lattice in 3D DRSC is shut down, the magnetic field gradient is switched on and quickly ramped to an excessive levitation gradient of∂B/∂z= 40.5 G/cm.After a holding time of 4 ms, the magnetic field gradient takes 2 ms to decrease to∂B/∂z=31.3 G/cm.We find that the application of the excessive∂B/∂zhas the advantages not only for improving the number of atoms loaded into the ODT but also for reducing the heating of atoms.The bias field is ramped toB=105 G within 6 ms to eliminate the horizontal anti-trapping potential induced by the application of the magnetic field gradient.

Fig.4.Optimization for the loading of the magnetically levitated ODT.(a) The number of atoms detected after 200 ms following the loading of the ODT as a function of excessive levitation field.The dots are the experimental data,and the solid line is the Gaussian fitting to guide the eyes.(b)The time sequence of magnetic field gradient ∂B/∂z and bias field B in the optimized loading of the ODT.
Based on the optimized parameters, we have loaded 1.8×107Cs atoms into the ODT.Here the number of atoms in the ODT is detected by directly imaging the atomic cloud after 200 ms following the loading of ODT.We find that the atomic cloud is heated to about 3µK after transferring into the ODT.We largely attribute the heating to the imperfect phase space matching.The atomic cloud after 3D dRSC has a 1/e of~350µm,but an equilibrium distribution in the ODT would have a 1/e of~100µm.Besides,the expansion of the atomic cloud in the levitation process leads to the increase of temperature.
3.3.Three-body recombination of atoms in the ODT
For the ultracold Cs atoms in the|6S1/2,F=3,mF=3〉state,the three-body recombination is the dominant loss mechanism.As shown in Fig.5, the number of atoms exhibits a strong three-body loss.[37]In the three-body recombination process,the interacting three particles collide and two of them form a dimmer, and then both the dimmer and the remaining particle escape from the trap.[38,39]The loss rate equation for the per-particle is given as ˙N/N=-L3〈n2〉, whereNis the number of atoms,L3is the three-body loss coefficient,andnis the atomic density.When away from unitarity,L3~¯ha4/mwith a dimensionless prefactor exhibiting a variation withain Efimov physics,[43]andais the s-wave scattering length.According to the atomic density distribution in 3D harmonic trap, the term including the average square density can be directly expressed asL3〈n〉2=βN2/T3with, anddenotes the geometrical mean of the trapping frequencies.By considering the collisions of atoms with the background gas as an additional loss term of-αN, we obtain a differential equation of the atom number,i.e.,
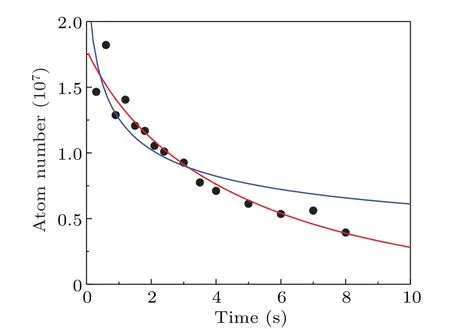
Fig.5.The number of atoms in the ODT as a function of time.The red line is obtained by using Eq.(8)to fit the data,and the fitted three-body loss coefficient is L3 =7.73×10-25 cm6/s.The blue line is obtained by using Eq.(9) to fit the data, where only the three-body loss is considered.The number of atoms shows a strong three-body loss before the intersection of two fitting curves at ~3.1 ms,and after that the onebody loss becomes the dominant mechanism in the atom loss.
At the large scattering length ofa=1418a0, the threebody recombination is so strong that both the dimmer and the third atom are immediately expelled from the trap, and the number of atoms exhibits a large three-body loss.The atoms undergoing three-body recombination have an average potential energy ofkBT/2,but the ensemble average is 3kBT/2.[37]The loss of an atom leaves an extra energy ofkBTin the remaining ensemble,and this leads to heating.The heating energy corresponding to the relative change in the temperature for the loss of one atom is related to the average energy.The rate of temperature change can be given by multiplying the loss rate of atom number:
By replacing the atomic loss rate,the evolution of temperature can be expressed as
Using Eq.(6)to substitute the termβN2/T3in Eq.(4),we can obtain the relationship betweenNandTas
whereN0andT0are the number of atoms and the atomic temperature after the loading of the atoms into the ODT.By applying Eq.(7)to Eq.(6),Ncan be eliminated and the variation ofTwithtcan be deduced analytically.The evolution of the atom number is derived by substituting the solution forTinto Eq.(7).The analytical expression of the atom number is given as
The three-body loss coefficient is derived asL3= 7.73×10-25cm6/s by using Eq.(8)to fit the experimental evolution of the atom number.
In addition, we try to consider only the three-body loss mechanism in the decay model of the atom number with the negligible collisions of atoms with the background gas, i.e.,the one-body loss rate isα →0 in Eq.(4).Equation (8) can be simplified as
However, Eq.(9) cannot provide an excellent fit for the data,as shown in the blue curve in Fig.5.Therefore the atom loss induced by their collisions with the background gas has to be taken into account.Two fitting results illustrate that the rate of three-body loss reduces with the decrease of atomic density,and the one-body loss becomes dominant.Our result also indicates the lifetime of atoms in the ODT is finally determined by the one-body loss from the collisions with the background gas.
4.Conclusion
We have used 3D dRSC to cool a large number of atoms to a cold temperature, which enables the loading of more atoms into a crossed ODT.The optimized excessive levitation is used to reduce the atomic velocity induced by the uneliminated gravity after switching off the lattice laser but before the magnetic field gradient reaches to the critical value to completely cancel the gravity.Compared to the loading of an ODT from a bare MOT or the gray-molasses cooling,there is a significant increase in the number of atoms by a factor of~10 and 3,and an decrease in the temperature by a factor of~50 and 5,respectively.
For the optically trapped ultracold Cs atoms,the number of atoms shows a fast decay because of a strong three-body loss at the large scattering length.We study the three-body recombination by analyzing the strong loss of Cs atom,and obtain the three-body loss coefficient by fitting the derived model to the experimental data.When the atomic density decreases continuously, we find that the one-body loss induced by the collisions of atoms with the background gas becomes dominant in the atom loss.Finally, the lifetime of atoms in the ODT is determined by the one-body loss.
Acknowledgements
Project funded by the National Key Research and Development Program of China(Grant No.2022YFA1404201),the National Natural Science Foundation of China (Grant Nos.62020106014, 92165106, 62175140, 12074234, and 11974331),and the Applied Basic Research Project of Shanxi Province,China(Grant No.202203021224001).
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- Corrigendum to“Reactive oxygen species in plasma against E.coli cells survival rate”
- Dynamic decision and its complex dynamics analysis of low-carbon supply chain considering risk-aversion under carbon tax policy
- Fully relativistic many-body perturbation energies,transition properties,and lifetimes of lithium-like iron Fe XXIV
- Measurement of the relative neutron sensitivity curve of a LaBr3(Ce)scintillator based on the CSNS Back-n white neutron source
- Kinesin-microtubule interaction reveals the mechanism of kinesin-1 for discriminating the binding site on microtubule
- Multilevel optoelectronic hybrid memory based on N-doped Ge2Sb2Te5 film with low resistance drift and ultrafast speed
