基于自适应波形分解与时频转换的风机工况诊断方法

黄子恒，许钊源，方辉，伍剑波*,，李晋航，石致远

基于自适应波形分解与时频转换的风机工况诊断方法

黄子恒1，许钊源1，方辉1，伍剑波*,1，李晋航2，石致远2

（1.四川大学 机械工程学院，四川 成都 610065；2.东方电气集团 中央研究院，四川 成都 611731）

目前针对风力发电机工况诊断方法的研究较为匮乏。为此，本文提出一种基于自适应波形分解和时频转换的诊断方法。该方法的算法采用了滑动间隔样本扩充、基于改进CEEMDAN的自适应波形分解方法、希尔伯特时频变换、VGG16神经网络。过程中，利用风机的振动加速度信号，通过自适应分解方法对信号进行分解降噪，将处理后信号进行变换生成二维时频谱，利用VGG16模型对时频谱样本集进行分类以达到诊断目的。为了评估该方法的有效性，将本文方法分别与传统模态分解、CNN模型进行对比，并对模型分类效果进行评估，结果表明，该方法具有更好的准确性。

风力发电机；波形分解；时频谱；VGG16

随着工业互联网的发展，机械设备的状态监测迈入了大数据时代，其具有海量数据、种类繁多、更迭极快的特点，这些都给机械状态诊断带来了新的挑战。以风力发电机为例，作为一种大型机械设备，其在全球应用颇多。但风力发电机组地处偏远，人工巡检故障排查困难[1]，给设备的运行维护带来了一定的困难。对风机的运行状态进行适时监测、预报和故障诊断，则是保证风机良好运行、企业生产正常进行的关键[2-3]。

基于信号处理与分析的诊断方法是现有设备工况诊断研究的重点。工程中通常可通过监测风机的振动、温度、转速等信号诊断风机轴承失效、机座松动、转子偏心等机械故障。发电机电气故障则通常通过监测发电机SCADA（Supervisory Control and Data Acquisition，数据采集与监视控制系统）信号参数，并对其进行处理后识别。李凤林等[4]利用总体经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）对信号进行分解，能够一定程度抑制间歇性噪音干扰，但是该方法依然存在模态混叠现象。王挺韶等[5]通过降噪编码器降噪，从噪音信号提取原始信号，从而提高在噪音环境下的故障识别效果。张龙[6]利用连续小波变换（Continuous Wavelet Transform，CWT）对输入信号进行时频变换，并将一维波形与二维时频谱进行融合，提高了故障诊断的精度。刘辉海等[7]使用自适应阈值作为风机故障检测的决策准则，有效检测重构误差的波动。

近年来，针对风力发电机的工作特点和运行工况，利用振动信号对风机进行状态分析与故障诊断受到越来越多的关注，目前研究主要集中在传动链和叶片单元。同时，有学者开展了基于模型的故障诊断研究，并采用了人工智能故障诊断技术。王博特等[8]通过对风电机组进行叶片振动测试，分析了叶片摆振和挥舞反向的振动特点，总结了影响叶片振动的相关因素。DONG等[9]通过高斯混合模型估计结构健康状态下振动加速度等数据服从的概率分布，并通过振动数据概率分布变化实现了实际服役环境因素影响下的风力涡轮发电机结构的损伤诊断。DAO等[10]基于振动信号以及SCADA数据分析实现风力发电机结构的损伤评估，虽然该方法提高了服役环境下振动状态监测可靠性，但疲劳裂纹等非线性损伤的监测效果仍有待提高。

研究显示，将经验模态分解与时频特征结合，能使信号在时频域上的分辨率更高，消噪和滤波效果好[10]，据此，本文提出一种基于改进完全噪音辅助聚合经验模态分解（Complete Ensemble Empirical Mode Decomposition with Adaptive Noise，CEEMDAN）[12]的自适应的波形分解方法。对原始信号进行分解重构，并通过希尔伯特变换[13]对降噪的信号进行时频转换，得到信号的时频分布，最后将时频图像输入VGG16神经网络来诊断风机工作状况。

1 算法基本原理

1.1 滑动间隔样本扩充

神经网络对训练样本中类别不平衡的问题十分敏感，这会使得模型训练效果下降，导致模型无法正确识别各个不同类别的特征分布。针对上述问题，本文选择使用“滑动间隔”来增加样本数量。

滑动间隔的具体方法为：从原始振动加速度数据集的第一个数据点开始，每隔slide个数据间隔点数，取长度为new，得到若干分割后的数据集，即为采样后的数据集。计算公式为：

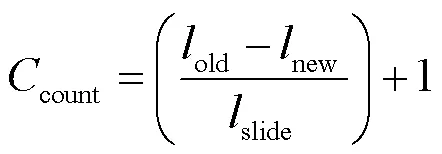
1.2 基于改进CEEMDAN的自适应波形分解方法

CEEMDAN在经验模态分解（Empirical Mode Decomposition，EMD）的基础上加入均值为0、方差为1的高斯白噪音[14]，来解决模态混杂问题。本文通过改变噪音加入策略，进一步减弱噪音干扰，其步骤如下。

（1）构造个随机高斯白噪音序列

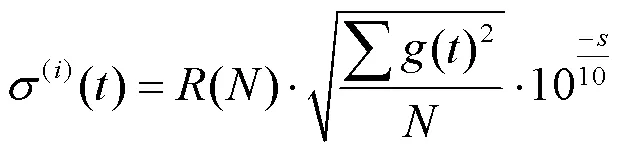
（2）将个信号添加个不同的随机高斯白噪音

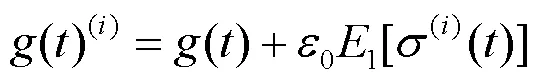
（3）求第一次迭代后含噪信号的残差，并对残差取平均

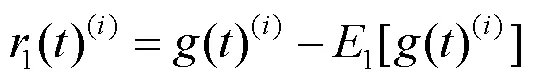
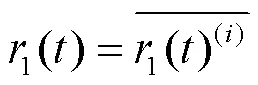
（4）求该方法下的第一阶模态分量

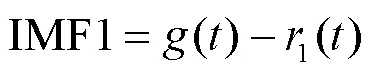
（5）使用步骤（2）中同样方法构造加噪数据集，进行次迭代。

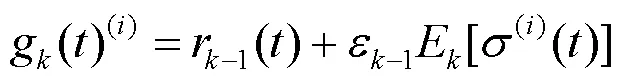
（6）由此得到该方法的第阶模态分量

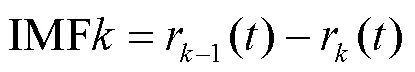
1.3 希尔伯特时频变换原理

希尔伯特变换是把一维的信号变成了二维复平面上的信号，其对于非平稳信号的处理和分析有很好的效果[15-16]，针对上文由自适应波形分解方法得到的信号分量，可得：

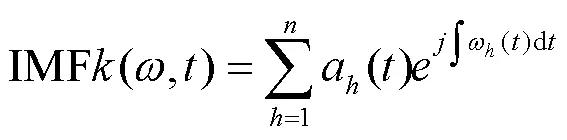
1.4 VGG16神经网络

VGG（Visual Geometry Group，视觉几何组）是一个利用GPU（Graphics Processing Unit，图形处理器）极高计算能力的深度卷积神经网络[17]，VGG16共由16层网络组成[18]。本文所用VGG16由3层全连接层和13层卷积层构成，利用池化层对卷积结果进行降维。除最后一层卷积层后采用LeakyReLU作为激活函数，其余各层卷积之后均采用ReLU作为激活函数。模型如图1所示。

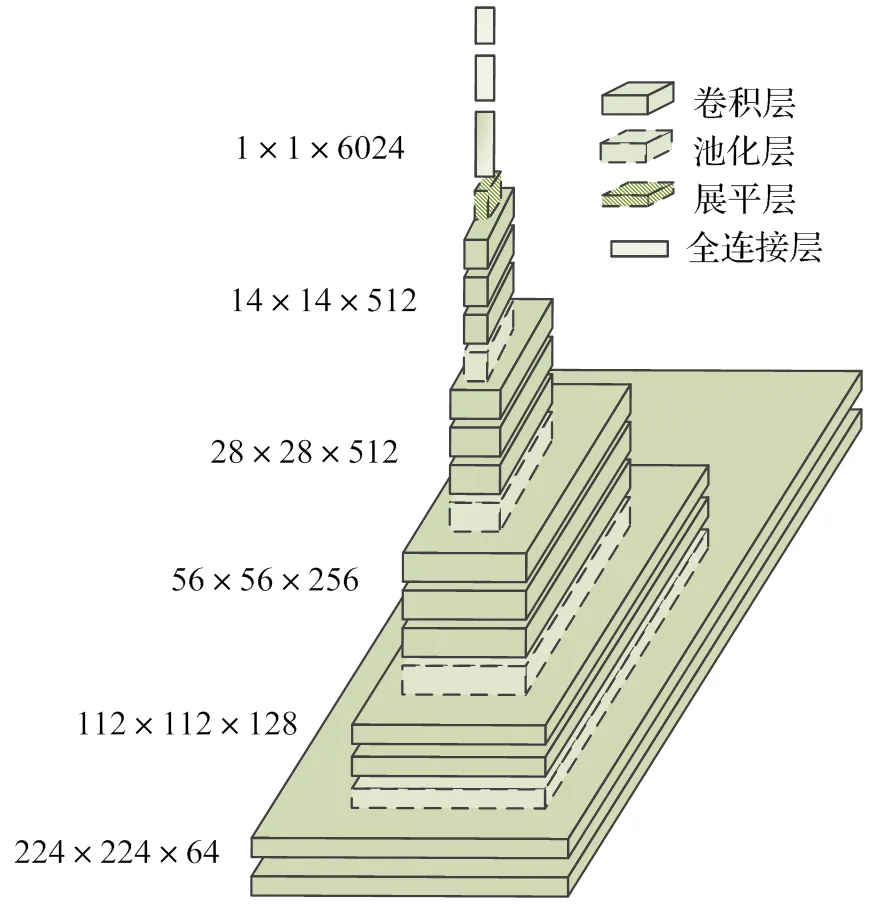
图1 VGG16网络结构图

针对多分类问题，本文采用交叉熵损失（CrossEntropy Loss，CE）作为网络模型的损失函数，其计算方式为：

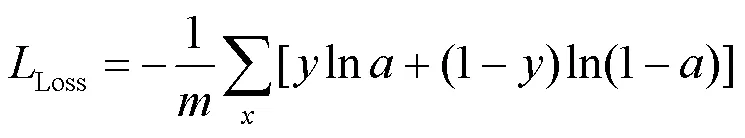
2 模型讨论与验证

2.1 自适应波形分解与时频转换的工况诊断流程

为验证本文提出方法的有效性，构造风机振动加速度样本集来分别进行波形分解和分类诊断模型的验证。采用广西某风电场2021年7月的运行数据，采集信号为风机振动加速度，数据统一为风机挥舞方向，采样频率50 Hz，包含正常运行、变桨、故障三种工况，共计2000条数据样本，每条数据由12000～15000个数据点组成，原始信号波形如图2所示。

首先对原始数据集样本进行采样与分割，针对数量较少的故障样本进行滑动间隔采样，针对数量较多的类别直接进行样本分割。为了既保证分割样本的完整性，又达到增加样本数量的目的，将新生成样本的长度定为设备一个旋转周期数据点数目的3倍，取滑动间隔长度为设备一个旋转周期点数的一半，由此将原始数据集的样本数量从2000条扩充至6024条。

然后将新数据样本进行自适应波形分解，每个样本得到若干子波分量，对分量按有效值进行排序，组合重构可得滤波后的样本。基于上述样本，利用希尔伯特变换将时域波形转换为时频域图像。将生成的图像集合按对应工况分类进行标签绑定，并按1:4的比例划分为测试集与训练集。训练集用以训练VGG16模型以达到诊断分类要求，测试集则用以检测模型效果。本文模型的具体诊断流程如图3所示。

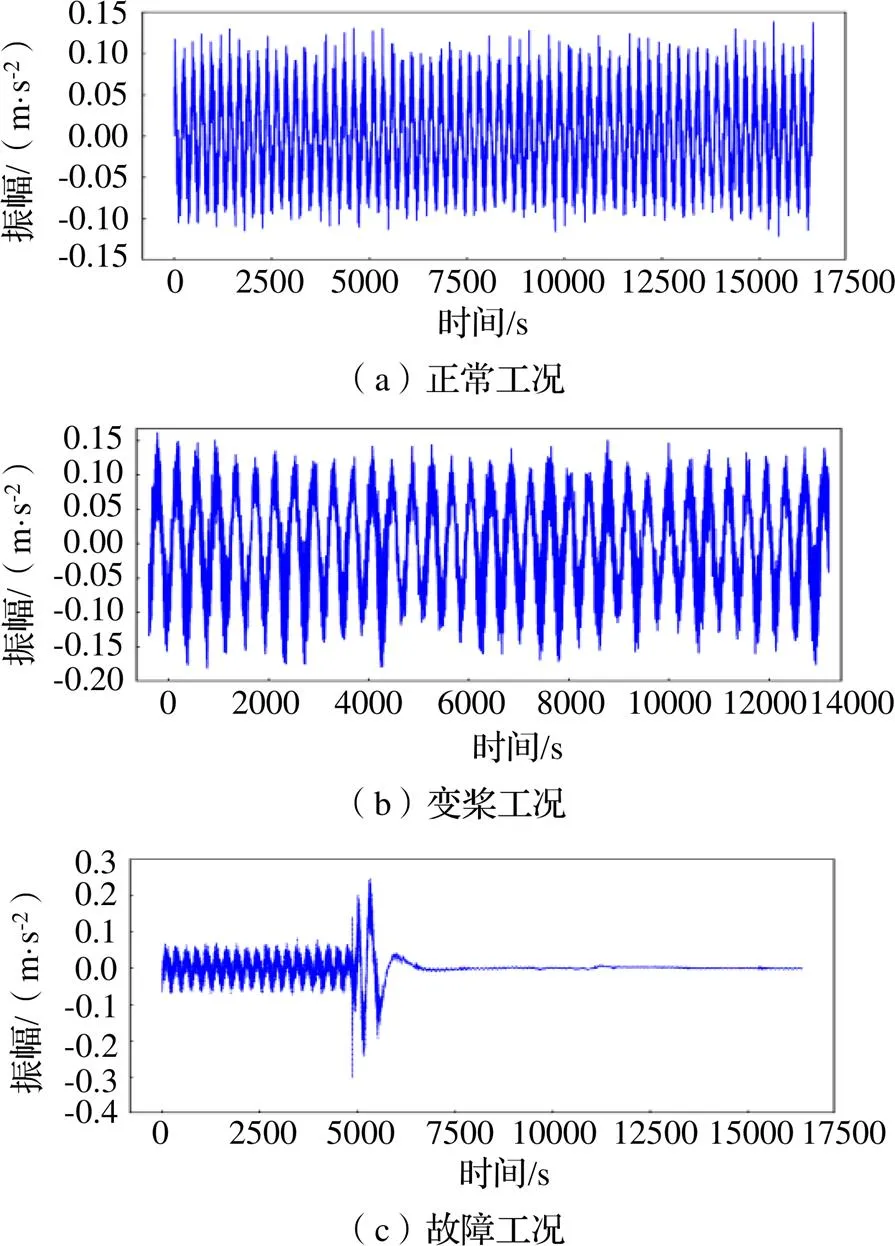
图2 三种工况下原始信号时域波形图

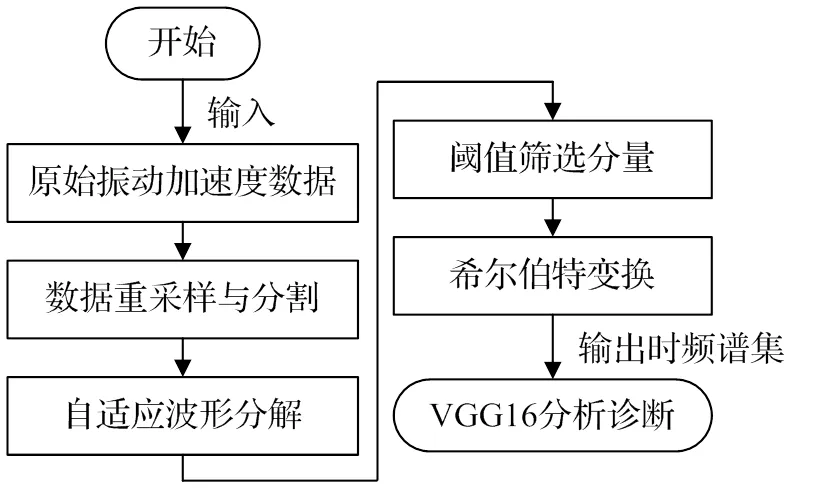
图3 诊断流程图

2.2 自适应波形分解与时频转换试验

选取正常工况下的振动加速度数据输入到自适应波形分解算法中。为验证有效性，本文选择与原始EMD方法进行对比，设置自适应分解的最大迭代次数为100次，添加噪音缩放比例为5%，两种方法波形分解结果如图4、图5所示，其中IMF1～4代表高频分量，其振动值的有效值趋向于0；而IMF5、6可看作为低频分量，其振动值的有效值不易趋近于0。可以看出，在分解结果方面，自适应波形分解下的分量IMF5和IMF6干扰较小，模态混叠现象较传统EMD方法减弱很多，而其余分量分解效果与EMD相当；在分解时间方面，原始EMD方法耗时60.02 s，自适应波形分解方法由于加入了噪音策略，分解耗时略长，为93.82 s，但综合考虑效果，该时长在工程可接受的范围内。因此证明自适应波形分解方法的优越性。

为获取风机状态关联的有效信息，选取有效值排序前5的分量进行波形重构，得到处理后的信号。对信号进行希尔伯特变换，将一维样本转成大小为(224, 224)的二维时频图像。

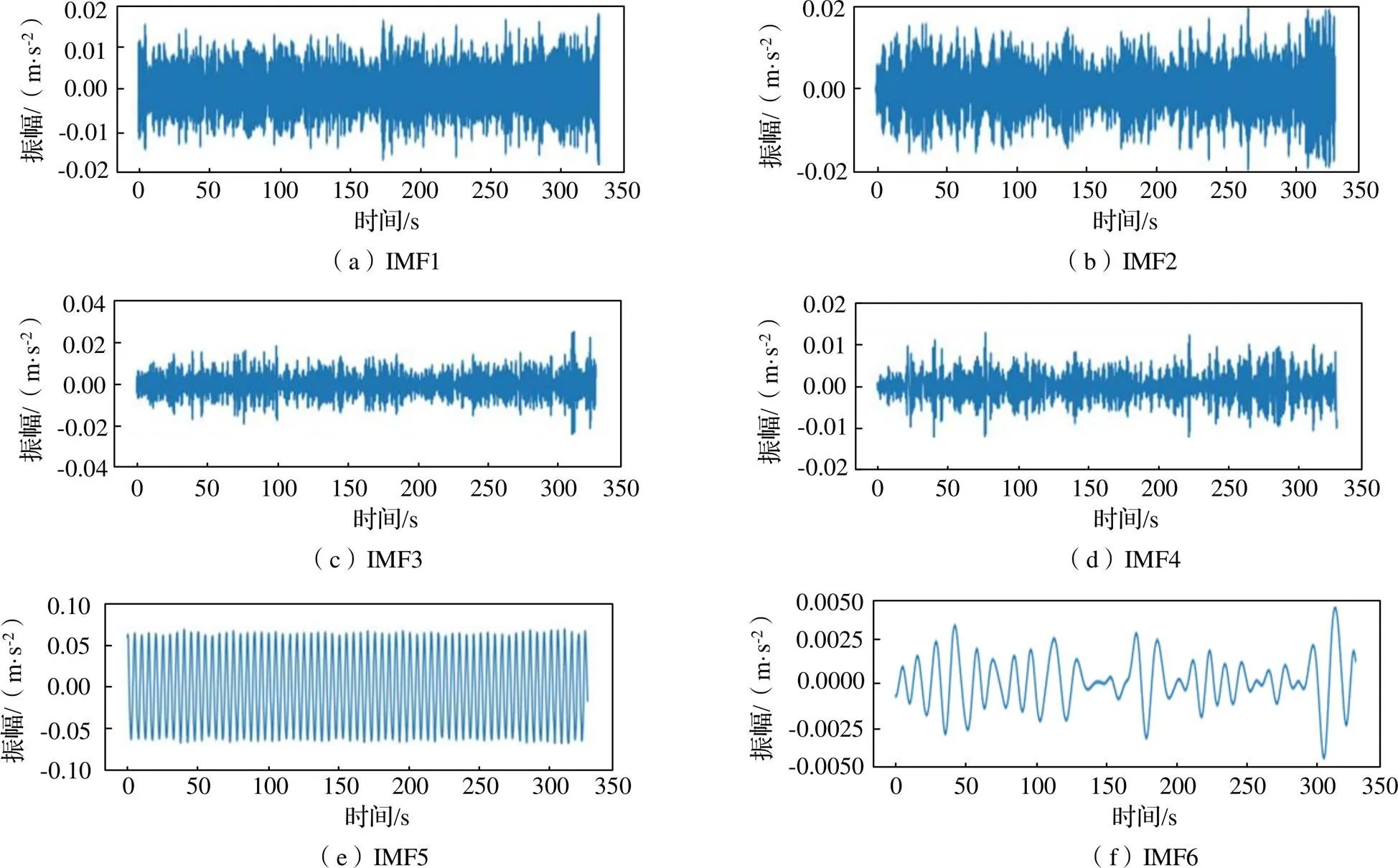
图4 EMD分解方法所得各分量图

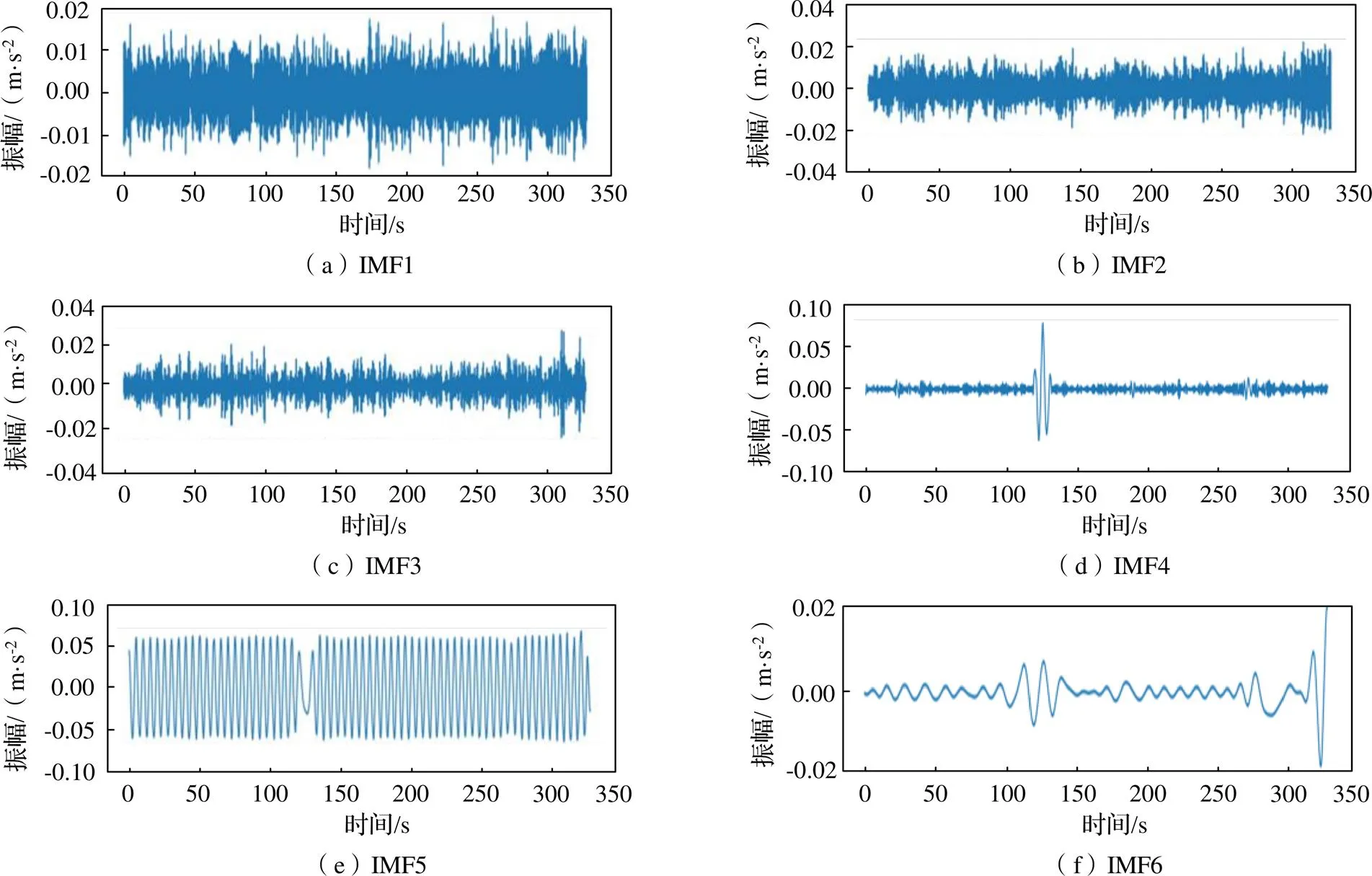
图5 自适应波形分解方法所得各分量图

为了验证本文方法在时频转换方面的可行性，采用STFT（Short-Time Fourier Transform，短时傅里叶变换）、EMD、EEMD与本方法进行时频转换对比试验。试验分解波形为一叠加了100 Hz、200 Hz、300 Hz频率的三角正弦仿真信号，采样频率为1000 Hz，最终生成时频谱如图6所示。时频谱图是IMF分量与对应能量分布的结合，每个时间与频率所对应的点代表的就是功率值。频谱图通过颜色对频率功率水平进行编码。黄色表示功率较高的频率成分；蓝色表示功率非常低的频率成分。

可以看出，受时间窗口、端点效应的影响，STFT和EMD方法均存在大量虚假模态分量，EEMD方法较前两者稍好，但300 Hz分量仍存在模态混杂现象，而本文所用自适应波形分解方法频率成分更加集中，可基本区分出100 Hz、200 Hz、300 Hz的分量。因此可以得出，自适应波形分解方法可以很好地应用于时频转换。

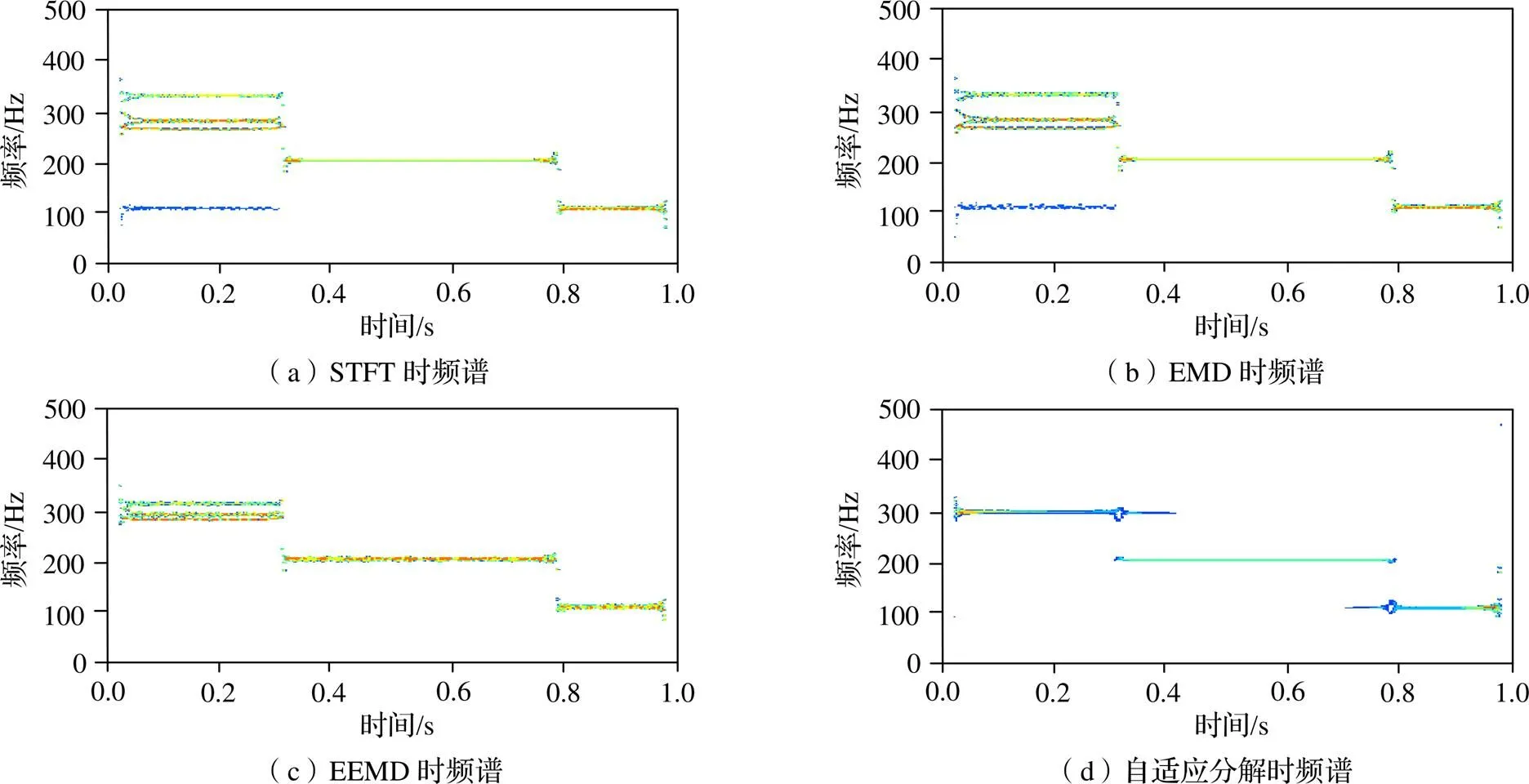
图6 不同方法时频转换对比

2.3 VGG16分类诊断试验

依据工作状态将数据分为三类：正常运行工况、变桨工况和故障工况。利用上文所述自适应波形分解方法进行时频转换，各状态时频谱示例如图7所示，图中用颜色深浅代表对应时间－频率下的频率幅值强弱。可以看出，正常状态下频率成分较为单一，主要为风机的工作频率；故障状态下频率杂乱，低频部分噪音明显增多。利用图像的纹理与色彩，神经网络可以进行后续的分类诊断。

本文构建的VGG16模型结构如表1所示，其卷积层均采用相同的卷积核参数，这样能使每一个卷积层与前一层张量保持相同的宽和高；池化层均采用相同的池化核参数，池化单元选用尺寸为2×2，步长为2；模型利用小尺寸卷积核等效大尺寸卷积核，故在特征提取效果相当时，多个小卷核与大卷积核相比，学习参数更少、计算量较小、训练更快速。该网络在构建时采用Dropout策略，可以防止模型训练过拟合的情况。经过偏置校正后，每一次迭代学习率都有个确定的范围，使参数比较平稳。

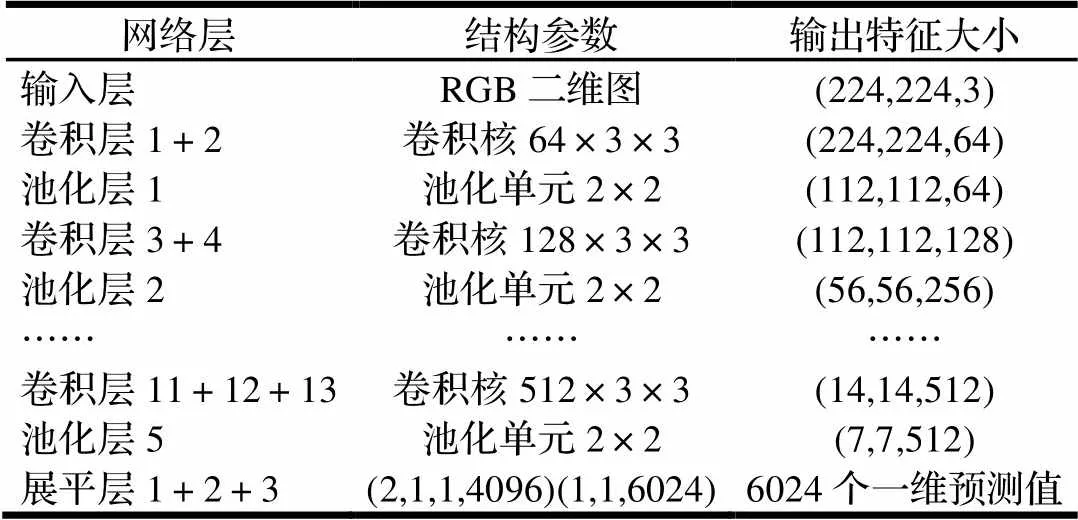
表1 VGG16网络结构图

为验证本文诊断模型的有效性，设置一组对比试验：将生成的时频谱样本集分别输入至本文VGG16模型和传统CNN（Convolutional Neural Network，卷积神经网络）模型中，进行各工况的分类测试，试验样本共计6024条，其中正常工况3024条，变桨工况2500条，故障工况500条。为了保证输入的随机性和普遍性，采用随机抽样[19]的方式生成训练集和测试集。试验所用工作站使用Windows 10操作系统，处理器为英特尔11代处理器i9-11900K，机带RAM为64 GB。

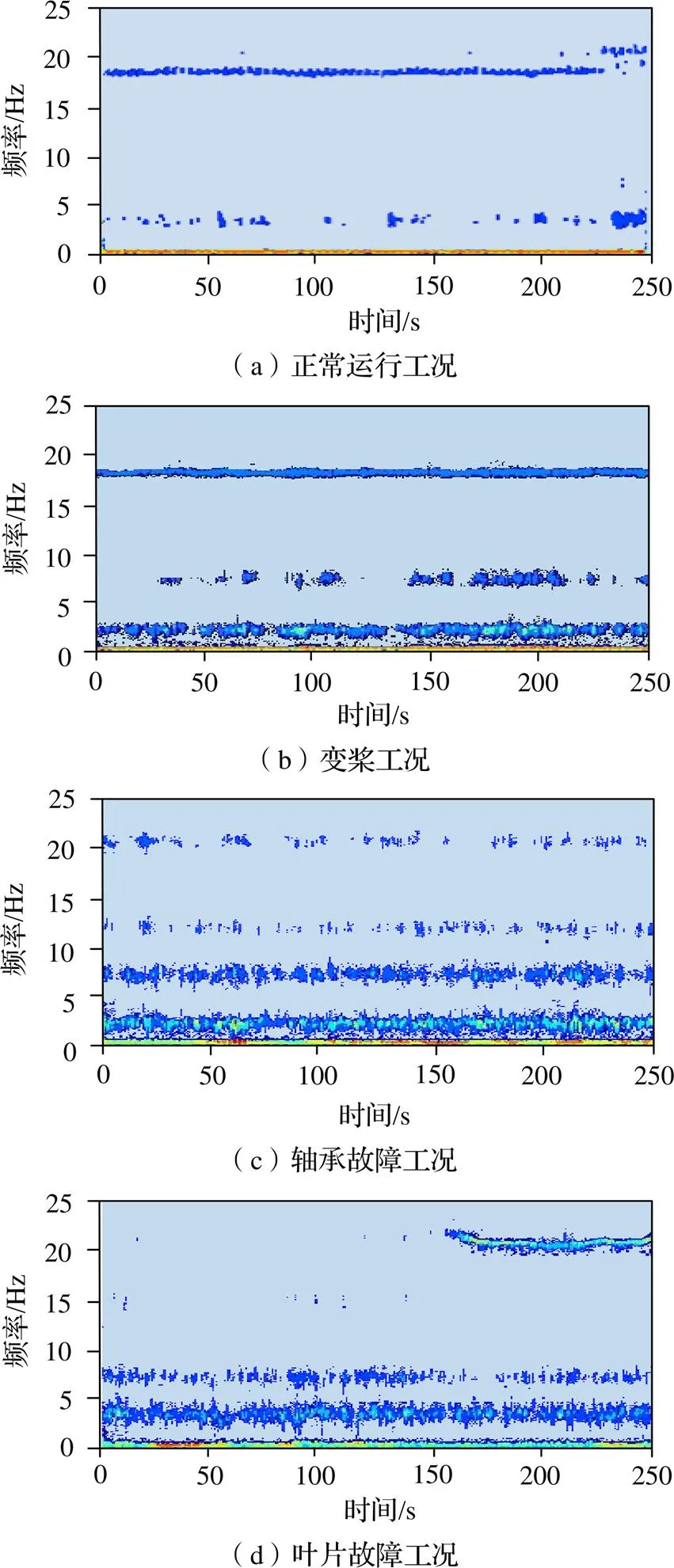
图7 各工况时频谱

本文选取的模型评价标准为准确率和损失值。准确率是在全部预测中，正确预测结果所占的比例；损失值是模型输出结果与真实值的偏离程度，本文使用交叉熵损失作为损失函数。

由图8可以看出，对于传统CNN模型，虽然验证集和训练集重合的最高准确率为92%，但模型并不稳定，10个迭代之后，验证集和训练集的波动较大，CNN模型并不能有效收敛。而在同样超参数设置下，本文所用VGG16模型可以快速收敛，且准确率在98%左右。证明基于本文的时频转换方法，VGG16模型可以达到更好更快的分类诊断效果。

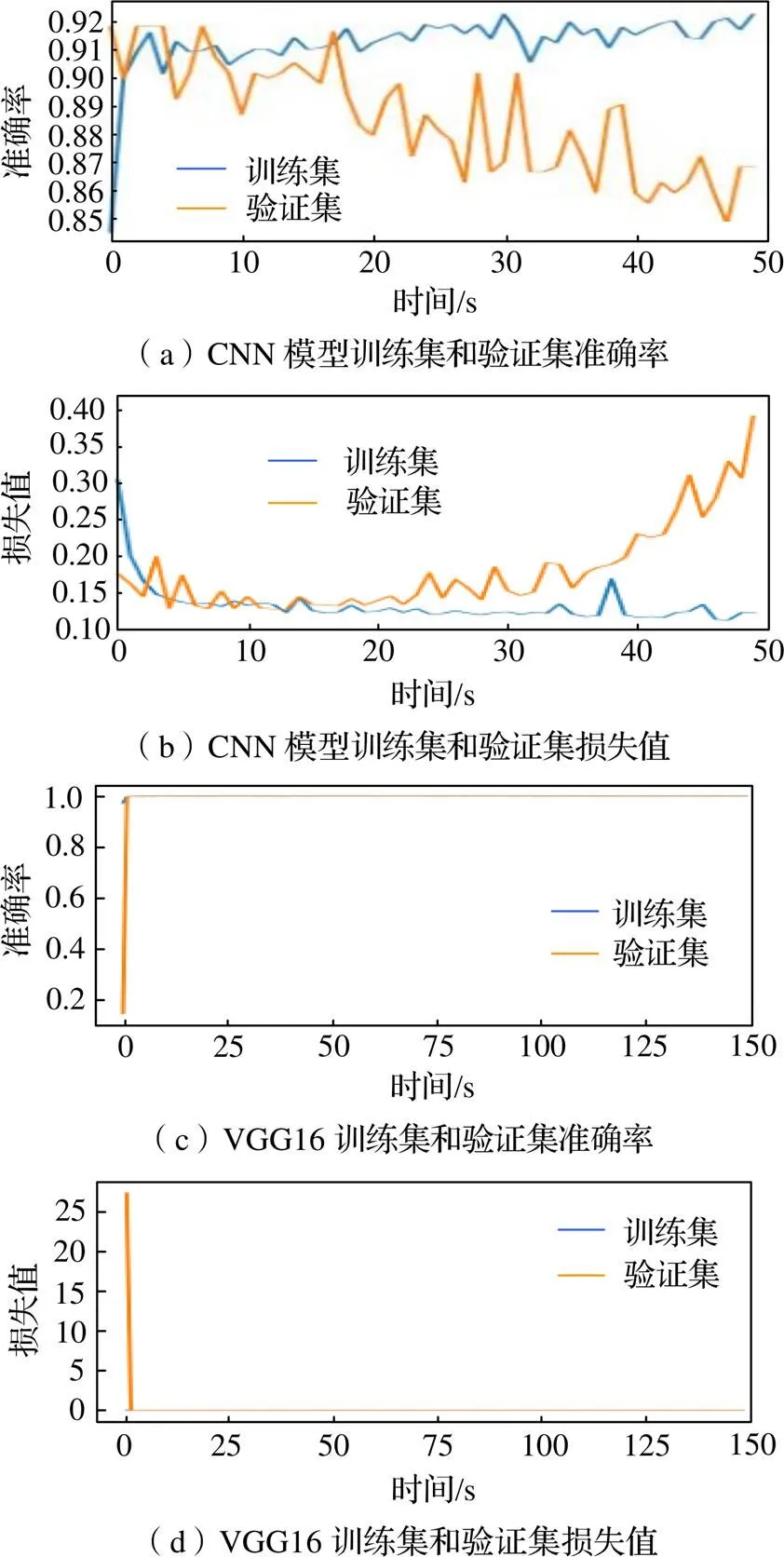
图8 模型识别结果对比

为测试本模型对本文数据的分类效果，将上述三类工况时频数据集输入至训练完成的VGG16网络中，预测结果如图9所示。可以看出，正常工况的样本完全预测正确，故障和变桨工况样本有误判现象，这一方面考虑为数据源不平衡所致，另一方面在实际工况中，较长时段的数据可能更加复杂多样，时频谱更加繁杂，且模型存在一定过拟合，泛化能力有待提升，但模型整体的预测准确性在可接受范围内。

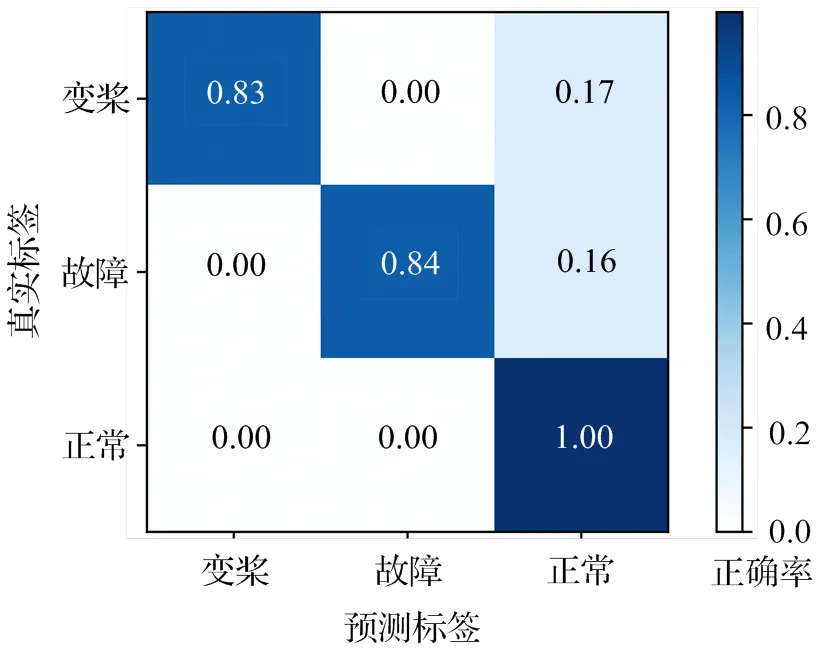
图9 VGG16预测结果混淆矩阵

3 结语

本文通过对风机振动加速度信号进行自适应波形分解，再将处理后的信号进行时频转换得到二维时频谱，将构造的时频样本集输入到VGG16模型中，进行风机工况分类诊断，可以得到以下结论：①在非平稳信号下，自适应的波形分解方法能够减少模态混杂的影响；②利用经过时频分析的二维样本与VGG16结合，可以实现风机工况信号特征的进一步抽取。

本文模型虽然在风力发电机的工况诊断中取得了较好的效果，但仍存在一定优化空间：①样本扩充存在一定的过拟合风险，对于不平衡数据的处理有待进一步研究；②目前的波形分解方法仍存在噪音干扰，可以与小波变换等方法相结合进一步滤波降噪。

[1]傅质馨，袁越. 海上风电机组状态监控技术研究现状与展望[J]. 电力系统自动化，2012，36（21）：121-129.

[2]王广斌，刘义伦，金晓宏，等. 基于时间序列分析的风机运行状态监测与预报及故障诊断[J]. 机械，2005（1）：21-23.

[3]黄子恒，许钊源，伍剑波，等. 基于优化模态分解和Xgblr的风机叶片故障诊断方法[J]. 机械设计，2022，39（7）：56-62.

[4]李凤林，杜红梅，巫忠书，等. 基于EEMD的列车车轮多边形故障诊断方法[J]. 机械，2021，48（5）：43-51.

[5]王挺韶，季天瑶，姜雨滋，等. 基于降噪自动编码器与一维卷积网络的风机故障诊断方法[J]. 电测与仪表，2020，60（1）：87-93，173.

[6]张龙，甄灿壮，熊国良，等. 基于深度时频特征的机车轴承故障诊断[J]. 交通运输工程学报，2021，21（6）：247-258.

[7]刘辉海，赵星宇，赵洪山，等. 基于深度自编码网络模型的风电机组齿轮箱故障检测[J]. 电工技术学报，2017，32（17）：156-163.

[8]王博特，王宇楠，郑涛，等. 大型风力发电机叶片振动测试与分析[J]. 噪音与振动控制，2021，41（4）：253-258.

[9]Dong Y，Fang F，Gu Y. Dynamic evaluation of wind turbine health condition based on Gaussian mixture model and evidential reasoning[J]. Journal of Renewable and Sustainable Energy，2013，5（3）：33117.

[10]Dao P B，Staszewski W J，Barszcz T，et al. Condition monitoring and fault detection in wind turbines based on cointegration analysis of SCADA data[J]. Renewable Energy，2018（116）：107-122.

[11]杨仁树，付晓强，杨国梁，等. EMD和FSWT组合方法在爆破振动信号分析中的应用研究[J]. 振动与冲击，2017，36（2）：58-64.

[12]Ren Y，Suganthan P N，Srikanth N. A Comparative Study of Empirical Mode Decomposition-Based Short-Term Wind Speed Forecasting Methods[J]. IEEE Transactions on Sustainable Energy，2015，6（1）：236-244.

[13]朱可恒，宋希庚，薛冬新. 希尔伯特振动分解在滚动轴承故障诊断中应用[J]. 振动与冲击，2014，33（14）：160-164.

[14]石琳，刘文慧，曹富军，等. 基于CEEMDAN-SVM-LSTM的高炉煤气利用率组合预测[J]. 中国测试，2022，49（1）：86-91.

[15]Huang N，Shen Z，Long S，et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society a-Mathematical Physical and Engineering Sciences，1998，454（1971）：903-995.

[16]Chen A，Wu W，Miao J，et al. Analysis of turbine-grid interaction of grid-connected wind turbine using HHT[C]. 2018 7TH International Conference on Clean and Green Energy，2018.

[17]Zhang X，Zou J，He K，et al. Accelerating Very Deep Convolutional Networks for Classification and Detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，2016，38（10）：1943-1955.

[18]朱曦. VGG16卷积神经网络的电路设计与FPGA验证[D]. 西安：西安电子科技大学，2020.

[19]黄哲学，何玉林，魏丞昊，等. 大数据随机样本划分模型及相关分析计算技术[J]. 数据采集与处理，2019，34（3）：373-385.

A Method for Wind Turbine Condition Diagnosis Based on Adaptive Decomposition and Time-Frequency Transform

HUANG Ziheng1，XU Zhaoyuan1，FANG Hui1，WU Jianbo1，LI Jinhang2，SHI Zhiyuan2

(1.School of Mechanical Engineering, Sichuan University, Chengdu 610065, China;2.The Research and Development Center, Dongfang Electric Corporation, Chengdu 611731, China )

At present, the research on the working condition diagnosis method of wind turbines is relatively lacking. In this paper, a diagnosis method based on adaptive decomposition and time-frequency transform is proposed. The algorithm of this method adopts the sliding interval sample expansion, the adaptive waveform decomposition method based on improved CEEMDAN, the Hilbert transform, and the VGG16 neural network. During the process, firstly, the vibration acceleration signal is decomposed and denoised by the adaptive decomposition method, the processed signal is transformed to generate a two-dimensional time spectrum, and the VGG16 model is used to classify the time spectrum set. In order to evaluate the effectiveness of the method, the method in this paper is compared with the traditional decomposition mode and CNN model. The performance of the classification is evaluated and the result shows that the method has better accuracy.

wind turbine；waveform decomposition；time spectrum；VGG16

TK83

A

10.3969/j.issn.1006-0316.2023.10.004

1006-0316 (2023) 10-0020-08

2022-09-23

四川省科技计划重点研发项目（2021YFG0039）

黄子恒（1996－），男，四川成都人，硕士研究生，主要研究方向为智能控制与故障诊断，E-mail：1738568615@qq.com。

通讯作者：伍剑波（1986－），男，四川眉山人，博士，教授、博士研究生导师，主要研究方向为智能控制与无损检测，E-mail：wujianbo@scu.edu.cn。