基于模糊PID的高速列车横向振动控制研究

牟如强, 陈春俊

(1.西南交通大学 机械工程学院,成都 610031,E-mail: scumrq2013@163.com;2.成都理工大学工程技术学院 自动化工程系,四川 乐山 614000;3.轨道交通运维技术与装备四川省重点实验室,成都 610031)

相比于主动悬挂系统,半主动悬挂系统不需要安装额外的能源装置,具有结构简单、能耗低等优点,因此具有广阔的应用前景[1]。针对高速列车半主动悬挂系统横向振动导致列车运行平稳性和安全性降低等问题,相关学者对高速列车横向振动控制算法进行了研究。文献[2]提出一种以车体横移振动为反馈的虚拟复合阻尼天棚控制算法,有效地改善了车体横向平稳性。文献[3-4]针对车体与构架横向振动矛盾关系,提出一种多目标约束下的混合半主动控制算法,同时提高了列车平稳性和脱轨安全性能。文献[5-6]设计了一种改进的线性连续型天棚-加速度阻尼(SH-ADD)半主动控制算法,提高了半主动悬挂在中高频区域的控制效果。文献[7]设计了一种基于开关型和连续型天棚阻尼的混合控制算法,通过优化系数,可以有效地改善列车横向平稳性。文献[8]运用经验模态分解,基于频域采样的三角级数法模拟轨道谱信号,重构得到不同频率的轨道激励,并对不同频率轨道激励下车辆横向振动和横向半主动悬挂天棚阻尼控制算法进行了研究。文献[9]以车体垂向振动加速度、二系悬挂垂向行程、构架垂向振动加速度、一系悬挂垂向行程均方根值为优化目标,应用评价函数法,建立了高速列车垂向减振器阻尼参数优化方法。模糊PID控制算法方面,文献[10]提出了一种用于航天器悬浮气垫重力补偿装置的模糊PID控制策略,仿真与实验结果验证了模糊PID在抗干扰和稳定性方面的优势。文献[11]提出了一种模糊PID控制策略,实现了电动汽车滑移率的有效控制。文献[12]基于高速列车半主动悬挂系统非线性模型的1/4车辆数学模型,设计了模糊自适应PID控制算法,仿真验证了算法的有效性。文献[13]基于萤火虫算法和反向传播(FA-BP)算法,提出了一种基于磁流变阻尼器的半主动可变论域模糊控制方法,可有效拟制振动。文献[14]为避免构架发生蛇行失稳现象,在磨耗轮轨接触状态时,以构架横向加速度和加速度变化率作为输入变量,以抗蛇行刚度和阻尼作为输出变量,设计了车辆半主动悬挂系统的混合模糊控制系统。文献[15]构造了高速列车横向半主动悬挂系统模糊控制结构,以减振器的实际阻尼力和车体、构架的横向振动加速度为反馈输入,对车体前、后端横向悬挂系统的可调减振器进行双闭环反馈独立控制,有效地拟制了车体的横向振动。文献[16]提出了一种模糊天棚阻尼控制算法,能够有效衰减车体横向振动加速度水平。文献[17]表明,模糊自适应PID控制算法可以有效提高交会气动载荷激扰下的车体横向平稳性。

总结发现,以上控制算法大多单独研究车体或构架的横向振动,由于车体和构架横向振动存在耦合,因此本文同时考虑车体和构架的横向振动,设计高速列车二系半主动悬挂横向混合阻尼模糊PID控制器,通过数值仿真,分析混合阻尼模糊PID控制算法的控制效果,为高速列车半主动悬挂系统的设计和应用提供一定参考。

1 高速列车半主动悬挂系统建模

1.1 27自由度横垂耦合振动模型

高速列车横向与垂向振动存在耦合关系,因此在17自由度高速列车横向振动数学模型的基础上[18],考虑车体浮沉与点头运动、构架浮沉与点头运动和轮对浮沉运动,建立27自由度高速列车横垂耦合振动数学模型[19],其简化模型如图1所示,模型输入、输出及符号如表1所示。

表1 27自由度横垂耦合模型输入、输出及符号

图1 高速列车简化模型

模型动力学微分方程矩阵表达式如公式(1)所示。

(1)

式中:M,C,K分别为质量、阻尼、刚度矩阵;G为轨道输入分布矩阵;w为轨道横向和垂向不平顺输入向量;X为27维状态向量,表示如下:

X=(yw1,yw2,yw3,yw4,ψw1,ψw2,ψw3,ψw4,zw1,zw2,zw3,zw4,
yt1,yt2,φt1,φt2,ψt1,ψt2,zt1,zt2,βt1,βt2,yc,φc,ψc,zc,βc)

1.2 测控系统建模

1.2.1 输入通道数学模型

根据文献[18]中的测量方法,搭建以车体和构架横向加速度为测量指标的测控系统输入通道,如图2所示。采用结构简单、制作容易、低频响特性好的应变片式加速度传感器来测量车体和构架的横移加速度。根据GB/T 5599-2019《机车车辆动力学性能评定及试验鉴定规范》要求,将加速度传感器对角布置在1、2位构架中心偏向车体一侧1 m的车内地板上,用于测量车体前、后端的横向加速度;将加速度传感器布置在1、2位构架端部轴箱上部,用来测量构架的横向加速度。

图2 测控系统输入通道方框图

车体和构架横向振动加速度输入通道传递函数如公式(2)和(3)所示:

(2)

(3)

1.2.2 输出通道数学模型

相比于可调开度减振器,磁流变阻尼器控制简单,响应速度快,因此选用磁流变阻尼器作为高速列车二系半主动悬挂横向可调阻尼执行器,磁流变阻尼横向振动测控系统输出通道如图3所示。

图3 测控系统输出通道方框图

如图3所示,输出通道传递函数如公式(4)所示:

(4)

磁流变阻尼器线圈电流i与阻尼系数C满足如下关系:

C=54.368 7i3-65.227 8i2+29.931 7i+2.474 7
(0≤i≤1.4)

(5)

2 模糊PID控制器设计

传统PID控制算法不需要建立系统的数学模型,通过设置合理的PID参数,便可以使被控系统具有较好的动态特性和稳定性,但对于非线性较强的系统而言,PID控制效果会有所降低。模糊控制是一种经验控制算法,适用于建模难度大的非线性系统。高速列车具有结构复杂、精确数学模型建模难度大、高阶非线性和时变等特点,因此将传统PID控制和模糊控制相结合,采用模糊PID控制算法来实现高速列车二系半主动悬挂横向阻尼控制。

2.1 模糊PID控制器基本结构

模糊PID控制器基本结构如图4所示。

图4 模糊PID控制器

图4(a)所示,设计了一个两输入和三输出的模糊PID控制器,以车体和构架横移加速度误差e和误差变化率ec为控制器输入,以Δkp,Δki,Δkd为控制器输出,模糊PID控制器的微分方程如下:

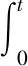
(6)

式中:kp0,ki0,kd0分别为比例系数、积分系数和微分系数初值;Δkp,Δki,Δkd分别为比例系数、积分系数和微分系数修正值;e(t),uc(t)分别为控制系统偏差和控制量。

图4(b)中,kj1,kj2分别为输入误差e和误差变化率ec的量化因子,ku1,ku2,ku3分别为输出模糊控制量ΔKp,ΔKi,ΔKd的比例因子。kp0,ki0,kd0分别为比例系数、积分系数和微分系数的初值。

2.2 模糊化

通过模糊化将误差e和误差变化率ec转化为模糊量E和EC,通过模糊推理得到模糊控制量ΔKp,ΔKi,ΔKd,然后通过清晰化将模糊控制量ΔKp,ΔKi,ΔKd转化为精确控制量Δkp,Δki,Δkd。文中将模糊量E和EC,模糊控制量ΔKp,ΔKi,ΔKd的模糊集均定义为集合F。

F={NB,NM,NS,ZO,PS,PM,PB}

F中的7个元素分别表示负大、负中、负小、零、正小、正中、正大。除模糊量E和EC模糊集中的元素零(ZO)采用高斯函数作为隶属度函数外,其余所有元素均采用三角形函数作为隶属度函数。其中,模糊量E和EC,模糊控制量ΔKp,ΔKi,ΔKd的变化分为7个等级,因此将其模糊论域均设置为:

{-6,-4,-2,0,2,4,6}

为确定模糊PID控制器的初值,通过数值仿真,分别得到被动控制和PID控制时车体和构架横移加速度,通过分析与计算确定车体和构架横移加速度误差e和误差变化率ec的变化范围,然后根据文中设置的模糊论域确定车体和构架横移加速度误差e和误差变化率ec的量化因子和PID初值;根据磁流变阻尼器线圈电流的取值范围确定模糊控制量的比例因子。本文将模糊PID的参数设置为:车体e和ec的量化因子分别为203.25, 7.50;构架e和ec的量化因子分别为43.57, 1.35;车体模糊控制量ΔKp,ΔKi,ΔKd的比例因子分别为0.42, 0.17, 0.017,构架模糊控制量ΔKp,ΔKi,ΔKd的比例因子分别为0.83, 0.001 7, 0.17;车体模糊PID控制时kp0,ki0,kd0分别为30, 1, 1,构架模糊PID控制时kp0,ki0,kd0分别为110, 0.01, 10。

2.3 模糊控制规则

本文采用如下思路设置模糊控制规则。当e和ec同号,且绝对值较大时,说明此时加速度误差和误差变化率较大,则采用较大的ΔKp,ΔKd,从而使误差快速减小;当e和ec同号,e绝对值较大,ec绝对值较小时,说明此时仅加速度误差较大,则采用较大的ΔKp,较小的ΔKi和ΔKd,从而减小误差;当e和ec绝对值均接近于0时,将ΔKp,ΔKi,ΔKd设置为0。由于模糊量E和EC均包含7个模糊子集,因此一共设置了49条模糊规则,如表2所示。

表2 模糊控制规则

2.4 模糊推理与清晰化

采用Mamdani模糊逻辑推理算法来推导模糊控制量U,推理公式如下[20]:

U=(E×EC)∘R

(7)

式中:U为模糊控制量,R为运算关系,“∘ ”为模糊关系合成运算。

采用面积重心法先将模糊控制量U转化为清晰量,然后对清晰量进行尺度变换得到能直接作用于执行器的精确控制量。面积重心法计算公式如下[20]:

(8)

式中:ucen为精确控制量,A(uj)为隶属度函数。

3 仿真分析

高速列车实车试验会影响列车的正常运营,试验前需要跟有关铁路部门协调沟通。此外,实车试验需要大量的测试设备,导致试验成本较高。由于现有条件有限,目前仅通过数值仿真方法来验证所提出的模糊PID控制策略的有效性。今后若具备条件,将进行实车试验验证。文中以我国某型动车组实际结构和真实参数建立了高速列车横向振动数值仿真模型,保证了模型精度,由此得到的数值仿真结果具有参考价值。

3.1 轨道不平顺输入

轨道不平顺是导致列车横向振动的主要原因,因此选择轨道方向不平顺、水平不平顺和高低不平顺作为高速列车横垂耦合振动模型输入,采用德国低干扰轨道谱,通过频域法模拟车速350 km/h时的轨道不平顺,模拟结果如图5所示。

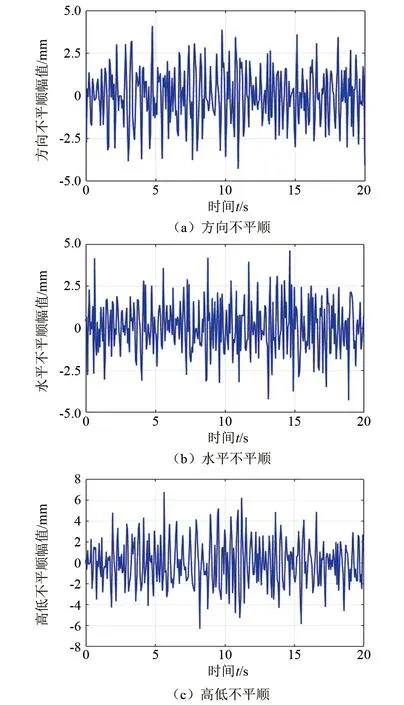
图5 轨道不平顺输入时域信号

如图5所示,轨道方向不平顺的幅值约为4 mm,轨道水平不平顺幅值约为5 mm,轨道高低不平顺幅值约为7 mm。

3.2 模糊PID控制效果分析

利用Simulink分别建立27自由度高速列车横垂耦合被动控制、车体模糊PID控制和构架模糊PID控制模型,其中二系半主动悬挂横向阻尼模糊PID控制器Simulink模型如图4(c)所示。通过仿真获得三种控制方式下车体和构架横移、侧滚、摇头、浮沉和点头加速度。仿真结果表明,模糊PID控制对车体和构架横移、侧滚和摇头加速均有影响,对车体和构架浮沉和点头加速度影响较小。车体和构架横移加速度时域特性、频域特性和功率谱密度(PSD)特性如图6～图8所示。

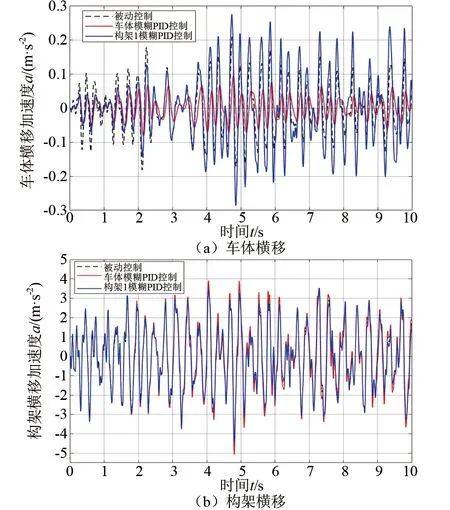
图6 车体与构架横移加速度时域特性

由图6可知,被动控制时,车体和构架横移加速度峰值分别为0.208 6和4.682;车体模糊PID控制时,车体和构架横移加速度峰值分别为0.095 8和5.082;构架模糊PID控制时,车体和构架横移加速度峰值分别为0.290 5和4.469。车体模糊PID控制使车体横向振动总体减小,使构架横向振动增大;构架模糊PID控制使构架横向振动总体减小,使车体横向振动增大。由图7和图8可知,车体和构架均表现为1 Hz～5 Hz的低频振动。被动控制时,车体和构架的主振频率峰值分别为0.046和1.022;车体模糊PID控制时,车体和构架的主振频率峰值分别为0.022和1.142;构架模糊PID控制时,车体和构架的主振频率峰值分别为0.071和0.922。车体模糊PID使车体主振频率峰值减小,使构架主振频率峰值增加,构架模糊PID的作用刚好相反。

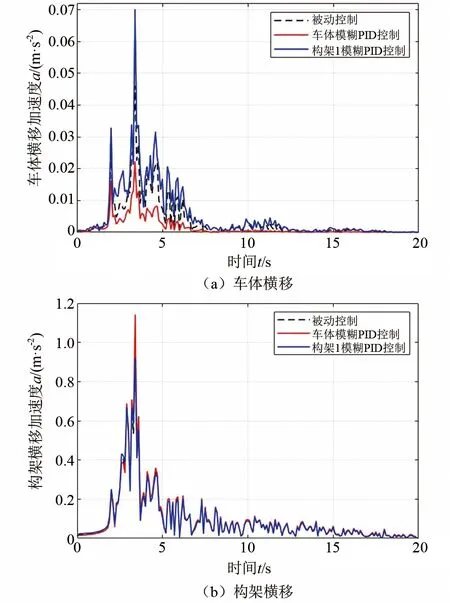
图7 车体与构架横移加速度频域特性

图8 车体与构架横移加速度PSD特性

由表3可知,相比于被动控制,车体模糊PID控制使车体横移加速度时域峰值、频域峰值和PSD峰值分别减小54.07%,52.17%,31.95%,使构架横移加速度时域峰值、频域峰值和PSD峰值分别增大8.54%,11.74%,13.52%。相比于被动控制,构架模糊PID控制使车体横移加速度时域峰值、频域峰值和PSD峰值分别增大39.26%,54.35%,18.43%,使构架横移加速度时域峰值、频域峰值和PSD峰值分别减小4.55%,9.78%,12.39%。综上所述,车体模糊PID控制和构架模糊PID控制存在矛盾关系。

表3 不同控制算法时车体和构架横移加速度

3.3 混合阻尼模糊PID控制器设计

为了使得高速列车车体和构架横向振动均满足要求,设计车体模糊PID和构架模糊PID各占一定权重的高速列车二系悬挂横向混合阻尼模糊PID控制器,混合阻尼C计算公式如下:

(9)

式中:λ为混合阻尼系数,且0≤λ≤1,Cc为车体模糊PID控制时二系半主动悬挂横向阻尼,Ct1,Ct2分别为构架1、2模糊PID控制时二系半主动悬挂横向阻尼,C为二系半主动悬挂横向混合阻尼。

3.3.1 混合阻尼系数λ对车体和构架横向振动的影响

由图9可知,随着混合阻尼系数λ变大,车体横移、侧滚和摇头加速度幅值和均方根RMS值均逐渐变小,车体横向振动逐渐变小,λ=1时,车体横向振动最小。

图9 混合阻尼系数λ对车体横向振动的影响

由图10(a)可知,随着混合阻尼系数λ变大,构架1和构架2横移加速度幅值逐渐变大,构架1横移加速度RMS值逐渐变大,构架2横移加速度RMS值先逐渐变小,然后逐渐变大。由图10(b)可知,随着混合阻尼系数λ变大,构架2侧滚加速度幅值逐渐变大,构架1侧滚加速度幅值、构架1和构架2侧滚加速度RMS值先逐渐变小,然后逐渐变大。由图10(c)可知,随着混合阻尼系数λ变大,构架2摇头加速度幅值基本保持不变,构架2摇头加速度RMS值逐渐变小,构架1摇头加速度幅值和RMS值逐渐变大。

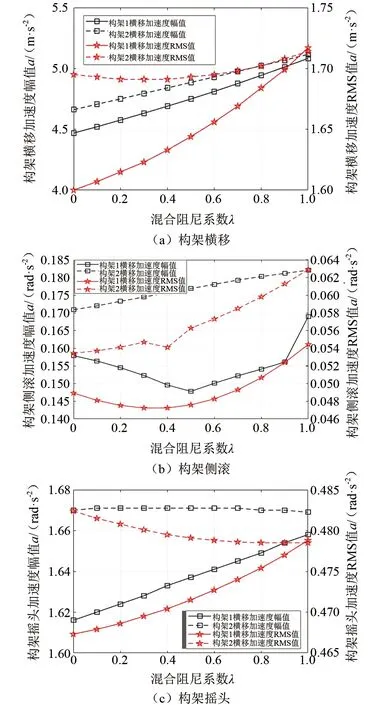
图10 混合阻尼系数λ对构架横向振动的影响

综上所述,混合阻尼系数λ对车体和构架横移、侧滚及摇头加速度均有影响,且呈现出矛盾关系,因此,实际应用时,应根据车体和构架横向振动情况,确定合适的混合阻尼系数λ,从而保证车体和构架均满足横向振动要求。

3.3.2 最优混合阻尼系数λ0

性能指标J不同时,最优混合阻尼系数λ0也不同。相比于幅值,均方根RMS值更能反映出车体和构架的横向振动情况,因此分别以车体和构架横移加速度RMS值之和最小为性能指标J1,以车体和构架侧滚加速度RMS值之和最小为性能指标J2,以车体和构架摇头加速度RMS值之和最小为性能指标J3,以车体和构架横移加速度、侧滚加速度、摇头加速度RMS值之和最小为性能指标J4,通过数值仿真,获得性能指标J1,J2,J3,J4与混合阻尼系数λ之间的关系曲线,如图11所示。

图11 混合阻尼系数λ对性能指标的影响

由图11(a)可知,随着混合阻尼系数λ变大,性能指标J1先缓慢减小,然后逐渐增大,性能指标J1的最优混合阻尼系数λ0=0.207;由图11(b)可知,随着混合阻尼系数λ变大,性能指标J2先迅速减小,然后逐渐增大,性能指标J2的最优混合阻尼系数λ0=0.814;由图11(c)可知,随着混合阻尼系数λ变大,性能指标J3先迅速减小,然后缓慢增大,性能指标J3的最优混合阻尼系数λ0=0.882;由图11(d)可知,随着混合阻尼系数λ变大,性能指标J4先迅速减小,然后迅速增大,性能指标J4的最优混合阻尼系数λ0=0.507。实际应用时,可以根据车体和构架横向振动的实际情况,选择合适的性能指标,从而实现车体和构架横向振动的综合控制。

3.3.3λ对车体横向平稳性的影响

平稳性是评估高速列车运行质量和安全性的重要指标,平稳性指标计算公式如下:

(10)

式中:W为平稳性指标,ai为车体加速度(m/s2),fi为振动频率(Hz),F(fi)为fi下的修正系数。

依据最新的GB/T 5599-2019《机车车辆动力学性能评定及试验鉴定规范》要求,分析车体横向振动加速度信号时,每5 s信号为一分析段,仿真时间为20 s,共4个分析段,对每一段进行快速傅里叶变换得到每段信号的频谱,终值为4段频谱平均值,将最终获得的ai与fi代入式(10)即可求出平稳性指标W。

由图12可知,被动控制时,车体横向振动平稳性指标W为1.747。采用模糊PID控制时,随着混合阻尼系数λ变大,车体的横向振动加速度平稳性指标W由1.92逐渐减小到1.39,车体横向振动平稳性等级为1级,评定结果为优。当混合阻尼系数分别为性能指标J1,J2,J3,J4所对应的最优混合阻尼系数0.207,0.814,0.882和0.507时,车体横向振动平稳性指标W分别为1.824,1.493,1.452和1.666。当混合阻尼系数0≤λ<0.354时,被动控制时车体横向振动平稳性优于模糊PID控制;当λ=0.354时,被动控制和模糊PID控制时车体横向振动平稳性相同;当0.354<λ≤1时,模糊PID控制时车体横向振动平稳性优于被动控制。综上所述,模糊PID控制可以有效改善车体横向振动平稳性。

图12 混合阻尼系数λ车体横向振动平稳性的影响

4 结论

数值仿真结果表明,建立的27自由度高速列车横垂耦合模型的车体和构架横向振动主频段为1 Hz～5 Hz,与实际情况相符,从而验证了模型的正确性。相比于被动控制,车体模糊PID控制使车体横移加速度时域峰值、频域峰值和PSD峰值分别减小54.07%,52.17%,31.95%;构架模糊PID控制使构架横移加速度时域峰值、频域峰值和PSD峰值分别减小4.55%,9.78%,12.39%,由此说明以上两种控制策略存在矛盾关系。

二系横向混合阻尼模糊PID控制时,混合阻尼系数λ越大,车体横向振动控制效果越好,构架横向振动控制效果越差。性能指标方面,以车体和构架横移加速度、侧滚加速度和摇头加速度均方根RMS值之和设计的性能指标Ji(i=1,2,3,4)的最优阻尼系数λ0分别为0.207,0.814,0.882,0.507。当0.354<λ≤1时,车体横向平稳性改善效果明显。本文为高速列车半主动悬挂系统的设计和工程应用提供一定研究思路。