基于改进Sigma点的无迹卡尔曼滤波水下目标跟踪算法

徐正兴，诸云，吴祎楠

（南京理工大学自动化学院，南京 210094）

1 引 言

海洋拥有广袤的资源，在经济、军事等领域占有重要地位，发展海洋成为世界发展不可或缺的一部分。因此，海洋资源的开发利用以及水下军事技术的发展受到了越来越广泛的关注［1］。水下的各种作业工具及其运动载体，是人类了解海洋、发展海洋的重要工具，其中水下航行器是探索水下世界的主要工具［2］。由于海洋中航行器的种类复杂、数量庞大，因此阵列所接收的信号也较为复杂，这些信号通常由多种水下航行器的辐射噪声、水上环境噪声和目标信号组成。同时，在复杂海洋环境（如水团、湍流、生物群体等）的作用下，一些混响、多途效应会使阵列接收信号变得更加复杂多变［3］，面对这样复杂的信号，微弱的目标信号掩埋在其中，若不对干扰信号进行抑制和消除，很难实现对弱目标的探测。目前较为广泛使用的水下目标跟踪算法有卡尔曼滤波算法以及扩展的卡尔曼滤波算法［4］，卡尔曼滤波算法开创了对噪声优化的先河［5］。在此基础上提出的扩展卡尔曼滤波算法则是较好地解决了非线性低阶系统的优化问题［6］，迈出从线性到非线性的跨越性一步。但是卡尔曼滤波使用的前提条件是已知噪声的协方差，过程噪声和测量噪声近似为白噪声，并且两者独立互不相干，因此对于非白噪声的干扰无法进行有效的抑制。而扩展的卡尔曼滤波算法只适用于低阶非线性系统，因此，为了对高阶的非线性系统的噪声干扰进行抑制，Julier等［7-9］基于近似概率分布比近似非线性函数或非线性变换要相对简单的思想，提出了采用无迹变换（Unscented Transformation，UT）结合卡尔曼滤波的无迹卡尔曼滤波算法（Unscented Kalman Filter，UKF）。文献［10］提出的算法实现了对运动噪声协方差矩阵的精确估计，具有较高的鲁棒性。文献［11］通过井下无线网络、惯性定位终端采集相关信息数据估算目标点最终的位置坐标。文献［12］有效提高了目标位置和速度的误差估计、可靠性及稳定性。文献［13］提出的算法具有更好的精度和稳定性。虽然以上算法在精度方面有所提升，但是提升的效果并不是非常显著，往往只有10%～20%的提升。因此，在此基础上本文所提出的基于改进Sigma点的无迹卡尔曼滤波水下目标跟踪算法（Improved Unscented Kalman Filter，IUKF）相对于无迹卡尔曼滤波等算法来说有着更为广泛的应用空间，在噪声的抑制、估计位置与实际位置、估计距离与实际距离的比对方面效果更好。本文的主要贡献：（1）本算法可以应用到水下航行器及声呐系统，具有一定的工程应用价值；（2）进行了二次无迹变换，使得基于Sigma点的更新值以及测量值更加的准确，从而大幅降低估计值以及预测值与真值之间的误差；（3）根据水下噪声干扰的特点，除了高阶线性以外，对于白噪声、低阶非线性等同样有着一定的抑制效果。经仿真实验验证，本方法在噪声抑制方面相比于其他算法可以取得较好的结果。

2 无迹卡尔曼滤波算法介绍

无迹变换［14］是在估计点附近确定采样，用这些采样点表示的高斯密度近似状态的概率密度函数。无迹变换实现方法为：在原状态分布中按某一规则选取一些采样点，使这些采样点的均值和协方差等于原状态分布的均值和协方差，将这些点代入非线性函数汇总，得到相应的非线性函数值点集，通过这些点集求取变换后的均值和协方差。这样得到的非线性变换后的均值和协方差精度最少具有2阶精度。对于高斯分布，可以达到3阶精度。其采样点的选择是基于先验均值和先验协方差矩阵的平方根的相关列实现的。

定义增广状态向量为

式中，令XX为水下航行器状态向量对应的Sigma点向量，XW为在航行器航行过程中所产生的噪声向量对应的 Sigma点向量，XV为观测噪声向量对应的Sigma点向量，按照增广状态向量的定义方式［15］，定义增广Sigma点向量为

UKF 算法的实现步骤如下：

①设定水下航行器的增广状态向量赋初值，给定协方差矩阵Pα0。

②记k时刻增广状态向量为协方差矩阵为Pαk，Sigma 点向量为

式中，α为可以进行设置的滤波器参数即比例缩放因子，κ为Sigma采样点间距离的比例因子，N为增广状态向量维数。

式（4）～（5）中，为Sigma点集Xi的均值对应的权值，为Sigma点集Xi的方差对应的权值。

③对时间更新进行计算，计算状态向量所对应的Sigma点的预测值，然后计算水下航行器先验状态估计值和航行器的先验协方差矩阵

式（6）～（7）中，无迹卡尔曼滤波算法的W(m)i为计算均值时对应第i个Sigma点的权值，W(c)i为计算协方差时对应第i个Sigma点的权值。

④对量测进行更新，以代替水下航行器状态变量，求取Sigma点的测量更新值，接着求取航行器的测量更新值和协方差矩阵PZk、PXkZk。

⑤求取滤波器增益矩阵，计算水下航行器的后验状态估计和状态协方差矩阵，

⑤完成后，返回②，计算下一时刻的水下航行器的状态估计值。无迹卡尔曼滤波算法的一些参数的设置如下。比例因子κ≥0 可以保证水下航行器协方差矩阵的正半定性，通常与增广状态向量的变量个数有关，为方便仿真，由于本实验的某个时刻的增广状态向量为单变量，故本文的比例因子κ=0。缩放因子α控制Sigma点的分布范围，0<α<1，通常为一个很小的正数，在本实验仿真中，令α=0.001。本文假设测量噪声满足高斯分布，参数的优化值反应状态历史信息的高阶状态特性，对高斯分布而言，参数的优化取值为2的时候最优，令λ=α2(N+κ)-N。

3 基于改进Sigma点的无迹卡尔曼滤波算法的介绍

3.1 系统的状态方程

假设水下航行器做匀速运动，水下航行器的初始位置为（X0，Y0），假设K时刻的位置为（Xk，Yk），假设初始速度为（Vx，0，Vy，0），K时刻的速度为（Vx，k，Vy，k），则X（k）=［Xk，Vx，Yk，Vy］，其中状态变量的关系为

则目标系统的运动状态方程为

式中，A为水下航行器状态转移矩阵，W（k）为系统状态噪声，G为过程噪声驱动矩阵，T为采样时间。

3.2 系统量测方程

假设岸基显控设备在水下任意位置，以岸基显控设备为原点，对水下航行器M进行跟踪，可以得到水下航行器M与岸基显控设备之间的X轴方向距离以及Y轴方向距离，如图1所示。

图1 量测模型Fig.1 Measurement model

由该水下航行器与岸基显控设备之间所得的X轴方向距离与Y轴距离可以得出在直角坐标系中，系统的量测方程为［15］

3.3 基于改进Sigma点的无迹卡尔曼滤波算法

本文提出的IUKF首先在原算法的第②步与第③步之间对Sigma点进行了再一次估计

由于水下航行器除了本身不可避免地会产生各种各样的噪声之外，还会受到周围环境的干扰噪声，因此将产生的噪声考虑进去后，对水下航行器的先验状态估计值和先验协方差矩阵的计算进行了一些改进使其可以较好地对噪声达到抑制效果。

式（19）～（20）中，G为过程噪声驱动矩阵，Q为输入白噪声w（k）的方差矩阵。接着进行二次UT变换，对水下航行器的先验状态估计值和先验协方差矩阵进行无迹变换

式中，参数λ=α2(N+κ)-N。这样进行UT变换所使用的则不是初始所给定的水下航行器的增广状态向量赋初值以及给定协方差矩阵Pα0，而是将所给定的水下航行器的增广状态向量赋初值以及给定协方差矩阵Pα0经过一次UT变换所得到的水下航行器的先验状态估计值和先验协方差矩阵，与初始的增广状态向量以及给定的协方差矩阵相比，经过了一次UT变换后得到的增广状态向量、协方差矩阵精度更高，再作为再次给定的增广状态向量以及给定协方差矩阵，这样再次进行UT变换的精度更高，与UKF算法相比，降低了估计值以及预测值与真值位置与距离之间的误差。IUKF的流程图如图2所示。

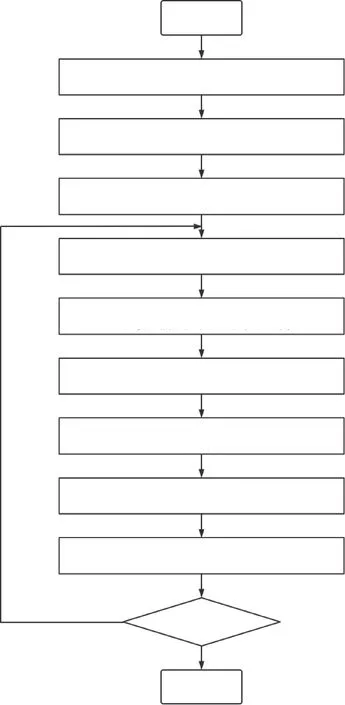
图2 IUKF的水下目标跟踪算法流程图Fig.2 Flow chart of IUKF underwater target tracking algorithm

4 仿真分析

4.1 仿真背景

以某水下航行器及其声呐系统［16］为研究对象，分别使用UKF以及IUKF对水下航行器的移动进行位置估计、距离估计。为避免偶然性，在平面随机模拟仿真选取一点为岸基显控设备，设定其坐标为（200，300），水下航行器初始位置为（-200，300），假设其在匀速运动，其在x轴上的运动速度为20 m/s，在y轴上的运动速度为4 m/s。假定随机噪声均满足高斯分布，模拟的白噪声的的方差矩阵为［0.0001 0；0 0.0001］，过程驱动噪声为［0.5 0；1 0；0 0. 5；0 1］，观测白噪声的方差矩阵为［0.001 5 0.05 0.001］；在观测过程中产生的观测噪声方差为5。为减少实验误差，将10次实验结果进行取平均值后再进行绘图，其实验结果如4.2节仿真结果所示。

4.2 仿真结果

4.2.1 UKF与IUKF下估计距离与实际距离对比仿真

图3～4是用UKF与IUKF对水下航行器与岸基显控设备距离的估计对比曲线。从图3可以看出，随着时间的增加，UKF对距离的估计与实际距离之间的偏差越来越大，而从图4可以看出，IUKF随着时间的增加，其估计距离与实际距离的曲线仍然贴合。IUKF相对于传统UKF对水下航行器与岸基显控设备实际距离的估计是更贴近实际距离的。图5～6是用UKF与IUKF对水下航行器与岸基显控设备局部估计距离与局部实际距离误差的估计对比曲线。随着时间的增加，使用UKF对水下航行器与岸基显控设备实际距离进行估测的误差随着时间的增大而变大，最终近似达到了18 m的误差，而使用IUKF对水下航行器与岸基显控设备进行估测的误差曲线一直在-3到3的误差带波动。

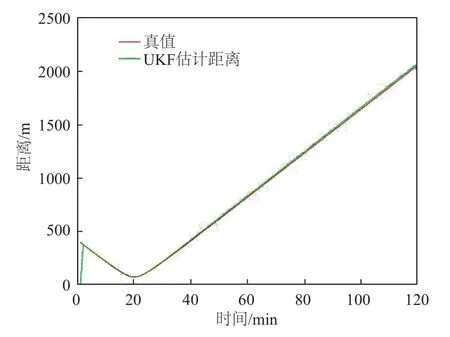
图3 UKF下估计距离与真值对比曲线Fig.3 Comparison curve of estimated distance and true value under UKF

图4 IUKF下估计距离与真值对比曲线Fig.4 Comparison curve of estimated distance and true value under IUKF

图5 UKF下局部估计距离与真值误差曲线Fig.5 Error curve of local estimated distance and true value under UKF

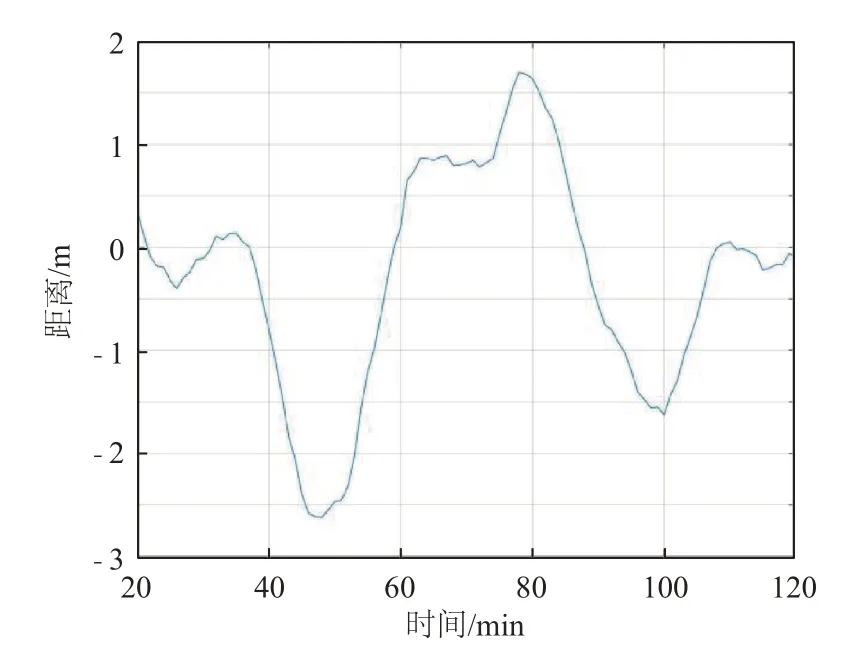
图6 IUKF下局部估计距离与真值误差曲线Fig.6 Error curve of local estimated distance and truth value under IUKF

4.2.2 UKF与IUKF下估计位置与实际位置对比仿真

图7～8是使用UKF与IUKF对水下航行器与岸基显控设备实际位置的估计对比曲线。随着时间增加，水下航行器与岸基显控设备估计位置与实际位置的误差变得越来越大，几米乃至几十米的误差在整体曲线图上很难显示出来，对于水下航行器与岸基显控设备实际位置的估计，UKF与IUKF的效果似乎相差不大。为了保证数据的严谨性，对前两条曲线的后面一段拿出来进行了量化研究。图9～10是用UKF与IUKF对水下航行器与岸基显控设备局部实际位置的估计对比曲线。当放大后，IUKF对水下航行器与岸基显控设备实际位置的估计与实际位置在曲线上较为贴合，而水下航行器与岸基显控设备的实际距离通过无迹卡尔曼滤波在放大后在曲线图上则有了略微的出入。接着计算出水下航行器与岸基显控设备局部估计距离与局部实际距离的误差。

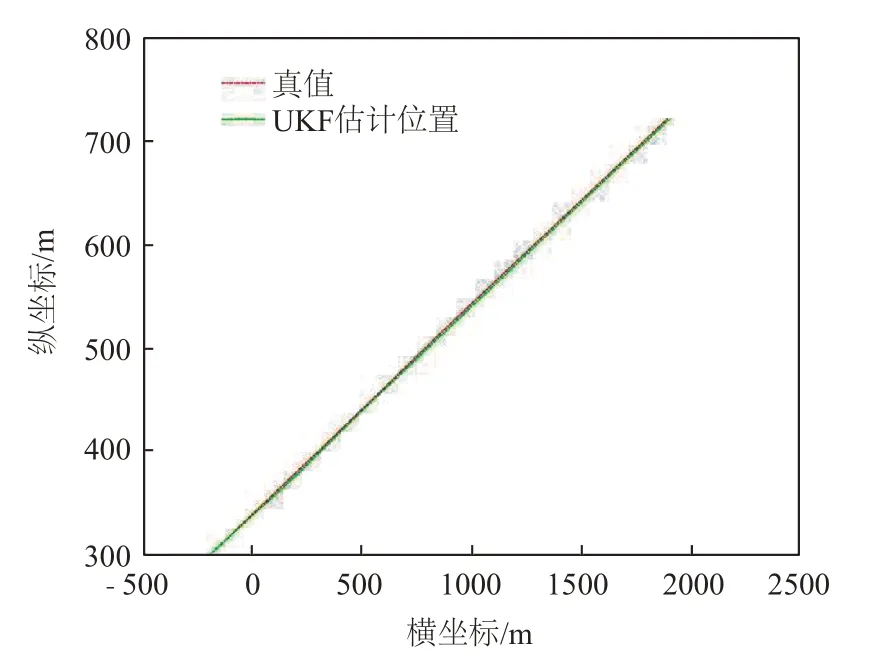
图7 UKF下估计位置与真值对比曲线Fig.7 Comparison curve of estimated position and true value under UKF

图8 IUKF下估计位置与真值对比曲线Fig.8 Comparison curve of estimated position and true value under IUKF

图9 UKF下局部估计位置与真值对比曲线Fig.9 Comparison curve of local estimated position and true value under UKF

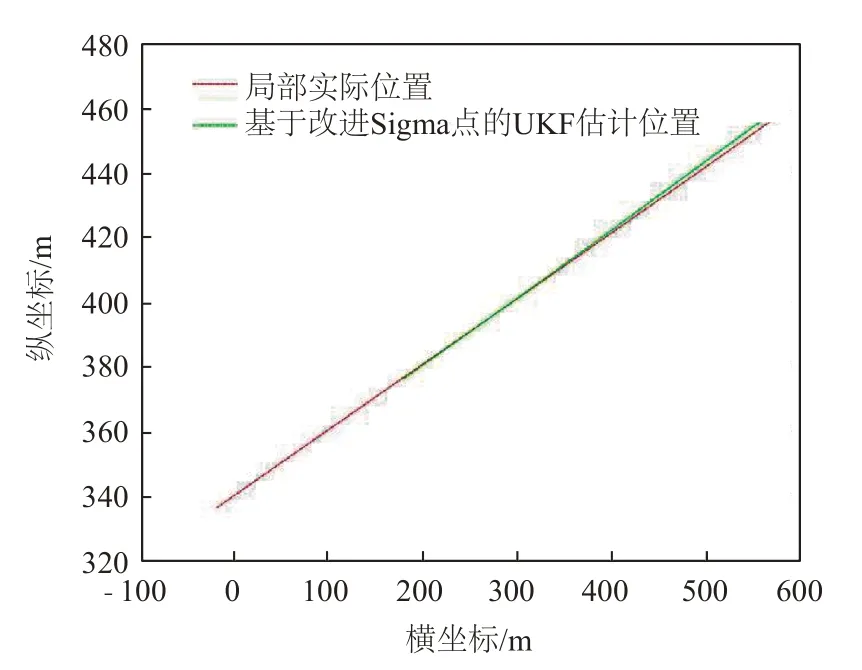
图10 IUKF下局部估计位置与真值对比曲线Fig.10 Comparison curve of local estimated position and true value under IUKF

4.2.3 UKF与IUKF对估计位置与实际位置偏差仿真

图11～12描述的是水下航行器与岸基显控设备估计距离、观测距离以及估计位置与实际位置的偏差。从曲线图中可以看出，使用UKF对水下航行器与岸基显控设备的观测距离与相应实际距离之间的误差在0的上下波动，并且误差峰值较多且相对较高，而使用IUKF对水下航行器与岸基显控设备的观测距离与相应实际距离之间的误差在0的上下波动，但是波动的峰值较低。使用UKF对水下航行器与岸基显控设备的估计位置与实际值之间的误差曲线属于随着时间呈上升状态，最终水下航行器与岸基显控设备之间的位置误差达到了18 m，而使用IUKF对水下航行器与岸基显控设备的估计位置与实际值之间的误差则不超过4 m，与传统的UKF相比误差降低了77.7%。并且随着时间的增加，IUKF对水下航行器与岸基显控设备的估计位置与实际之间的误差也一直处于10 m之内。

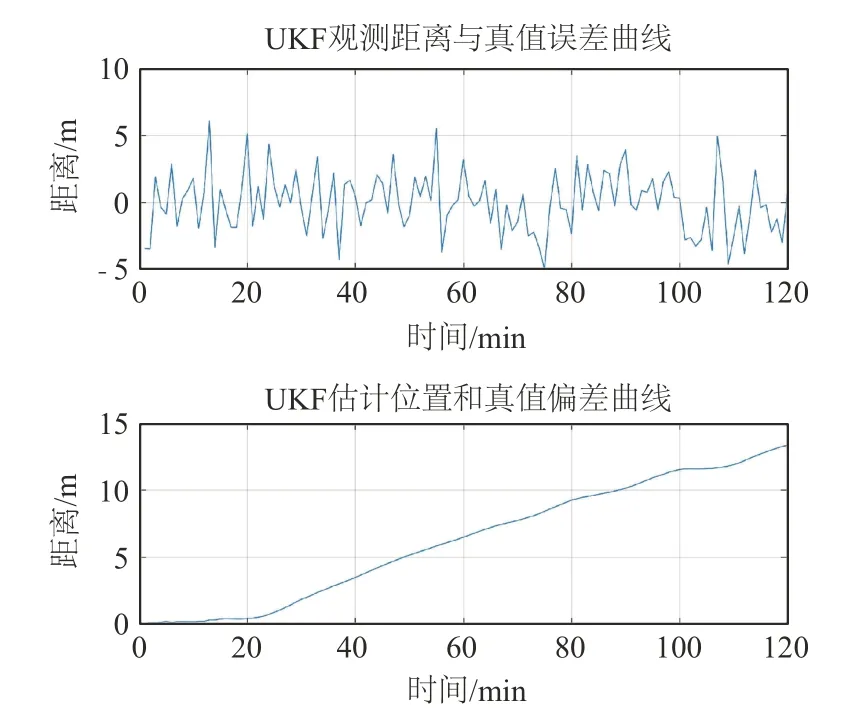
图11 UKF下估计、观测值与真值误差曲线Fig.11 Error curves of estimated,observed and true values under UKF

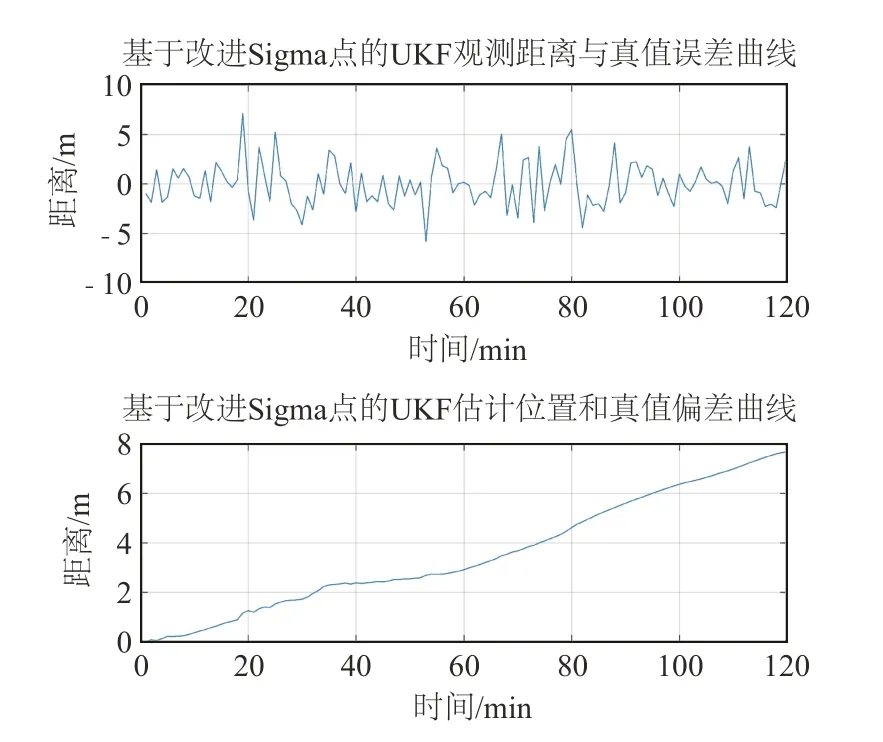
图12 IUKF下估计、观测值与真值误差曲线Fig.12 Error curves of estimated,observed and true values under IUKF

假设UKF估计位置和真值偏差为M，IUKF估计位置和真值偏差为N。UKF估计距离和实际距离误差为m，基于改进Sigma点的UKF估计距离和实际距离误差为n，则

如表1所示，使用传统的UKF对水下航行器与岸基显控设备的估计位置和真值之间的偏差在120 s内达到了13.8 m，对水下航行器与岸基显控设备的估计距离和实际距离之间的偏差峰值达到了17 m，而使用IUKF对水下航行器与岸基显控设备的估计位置和真值之间的偏差在120 s内仅仅达到了7.9 m，与使用UKF对水下航行器与岸基显控设备的位置进行估测相比精度提升了42%以上，与此同时，水下航行器与岸基显控设备的估计距离和实际距离之间的偏差峰值也仅为2.7 m，与使用UKF对水下航行器与岸基显控设备的距离估测相比精度提升了86%。

表1 UKF与IUKF估计位置、估计距离与真值误差表Table 1 UKF and IUKF estimated position,estimated distance and truth error table

5 结 论

本文以位置以及速度作为状态变量，以某水下航行器及其声呐系统为研究对象，分别使用无迹卡尔曼滤波算法以及IUKF对水下航行器与岸基显控设备进行了位置估计、距离估计［17］。主要对水下航行器与岸基显控设备的估计位置与实际位置进行了对比分析，对水下航行器与岸基显控设备的估计距离与实际距离进行了误差对比分析，对水下航行器与岸基显控设备的估计位置和真值偏差曲线进行了对比分析。还分别对比了UKF以及IUKF的滤波效果，仿真结果在肯定了UKF的基础上也同样证明了IUKF的滤波的实用性，尤其是在对水下航行器与岸基显控设备的估计距离与实际距离的误差降低以及对估计位置和真值偏差降低方面取得了显著的优化效果，并且IUKF通过二次UT变换还使得精度更高，水下航行器与岸基显控设备的估计距离与实际距离的误差相对UKF降低了86%，估计位置和真值的偏差相对UKF降低了53%，这在图10和图12中有着很好的体现。

海洋拥有广袤的资源，在经济、军事等领域占有重要地位，发展海洋成为世界发展不可或缺的一部分。在国家海洋强国战略的引导下，海洋装备的研究与发展已成为研究热点与重点，其中水下航行器更是探索水下世界的主要工具。在提出IUKF并成功实现水下航行器与岸基显控设备的估计距离与实际距离的误差以及估计位置和真值偏差的降低后，接下来将会在此基础上引入更为复杂的强干扰，实现水下航行器与动态目标的估计距离与实际距离的误差以及估计位置与真值偏差的降低。