全站仪加常数和乘常数测量不确定度研究

2023-11-01张子达杨维芳姬晓晓李文辉

计量学报 2023年9期

张子达, 杨维芳, 姬晓晓, 李文辉

(1.兰州交通大学测绘与地理信息学院，甘肃兰州730070；2.地理国情监测技术应用国家地方联合工程研究中心，甘肃兰州730070；3.甘肃省地理国情监测工程实验室，甘肃兰州730070；4.甘肃省测绘产品质量监督检验站，甘肃兰州730070)

1 引言

全站仪不仅是地理空间数据采集、变形监测和建筑物放样工作不可或缺的精密仪器,还在诸如自行火炮身管指向测量、大型立式储罐容量标定等领域用于高精度测量工作。为了保证测量精度和测量结果的可靠性,必须对全站仪进行定期检定。其中加常数和乘常数测量是全站仪测距检定中的重要检定项目,其检定采用野外基线法,依据JJG 703-2003《光电测距仪检定规程》[1]在野外足够长的基线上,按照基线分段原理选取多个固定点,形成21段组合距离,并用较高精度的测距方法(维塞拉干涉仪或因瓦基线尺测距等)测量固定点之间的距离值作为标准值,然后使用待检仪器测量21段距离,将观测值与基线标准值进行比较,依据最小二乘原理进行平差计算得到加常数、乘常数。

目前测绘仪器检定实验室的检定流程并未提供加常数和乘常数测量的不确定度评价[2,3]。而测量不确定度是表征测量结果质量的量化参数,脱离不确定度将测量结果与规程/标准中的参考量比较,进行仪器检定项目是否合格的判定是不严谨的。中国合格评定国家认可委员会发布的规范CNAS-CL07:2011《测量不确定度的要求》中明确指出[4]“检测实验室应有能力对每一项有数值要求的测量结果进行测量不确定度评估,当不确定度与检测成果的有效性或应用有关、或在用户有要求时、或当不确定度影响到对规范限度的符合性时,必须提供测量结果的不确定度。”ISO/IEC 17025《检测和校准实验室能力通用要求》中也要求[5]“开展检测的实验室应评定测量不确定度”以及“当测量不确定度与检测结果的有效性相关时”,实验室应明确判定规则,并在报告中出具相应的测量不确定度。因此测绘仪器检定实验室进行检定工作时必须考虑测量不确定度。

本文以TS06power-2″型号全站仪的加常数和乘常数测量为例,采用GUM法与MCM法2种方法评定加常数、乘常数测量结果的不确定度[6～9],并对评定方法及其结果进行比较与分析。

2 数学模型

根据加常数与乘常数测量方法可得出计算公式:

Di=Li+K+Di·R

(1)

式中:Di为各段基线的标准值;Li为待检仪器测量基线经过气象、倾斜改正后的观测值;K为待检仪器的加常数;R为待检仪器的乘常数;i为观测次数(i=1,2,…,n)。

进而:

βi=K+Di·R

(2)

式中:βi为基线标准值与观测值的差值,即

βi=Di-Li

(3)

共有21段基线标准值与观测值,即共进行了21次测量,可得出21个观测方程。按照最小二乘原理进行平差计算可得出加常数K和乘常数R的计算公式[1]:

(4)

(5)

根据《光电测距仪检定规程》测距单次测量标准偏差的计算公式与加常数和乘常数的标准偏差公式为[1]:

(6)

(7)

(8)

(9)

(10)

(11)

式中:m0为测距单次测量标准差;mK为加常数的标准偏差;mR为乘常数的标准偏差;vi为观测值的残差;Q11为加常数的灵敏度系数;Q22为乘常数的灵敏度系数。

由式(3)可表示1次独立观测的差值,则m0可表示差值βi的标准不确定度[10,11]。又由式(6)可知m0由观测值残差估计得来,而测量不确定度要求包含所有误差来源,所以从测量不确定度角度来说,m0的估计值并不能完整地表示单次测量的不确定度。单次测量的不确定度应该使用不确定度评定的方法进行评定[12～14],加常数和乘常数的标准不确定度同理。本文通过评定单次测量的不确定度u(βi)进而得到加常数的不确定度u(K)和乘常数的不确定度u(R)。由式(7)和式(8)可得:

(12)

(13)

3 GUM法评定不确定度

GUM法采用的是1个输入输出模型,即输出量是输入量的1个函数。将输入量的估值与标准不确定度按照线性化的模型进行传播,得到输出量的估值和标准不确定度;再假设中心极限定理适用,进而计算包含因子与扩展不确定度。因此使用GUM法要求[6,7]:

(1) 计算所有输入量的估值与不确定度作为不确定度分量;

(2) 数学模型的非线性化不显著;

(3) 中心极限定理适用,即输出量的概率密度函数为高斯分布或者t分布。

分析加常数、乘常数检定方法与步骤,不确定度主要来源[13～16]有待检仪器测量重复性引入的不确定度、待检仪器分辨力引入的不确定度、气象改正引入的不确定度、标准基线测量引入的不确定度、标准基线长度变化引入的不确定度。

3.1 测量重复性引入的测量不确定度分量

将待检仪器与反射棱镜置于室内约30 m距离的两端,操作仪器照准棱镜后连续读数30次并记录,计算30次读数的平均值为29.995 8 m,再计算每次读数与平均值的差值后得到表1数据。

表1 测量重复性检定数据Tab.1 Measurement repeatability verification data

由贝塞尔公式可得:

(14)

3.2 分辨力引入的测量不确定度分量

在约30 m的距离两端分别放置待检仪器和分辨力检验台,然后将仪器照准反射棱镜重复测距10次,计算平均值为测距值。

将棱镜从检验台零刻度处开始每次移动1.1 mm,共移动10次,将平均观测值先与归零后距离值作差,再和间隔值作差得到差值,计算后得到表2数据。其中归零后距离值是10组距离平均观测值归零后(减去间隔值)的距离平均值,即将每组平均观测值减去间隔值后相加,然后除以10取平均。

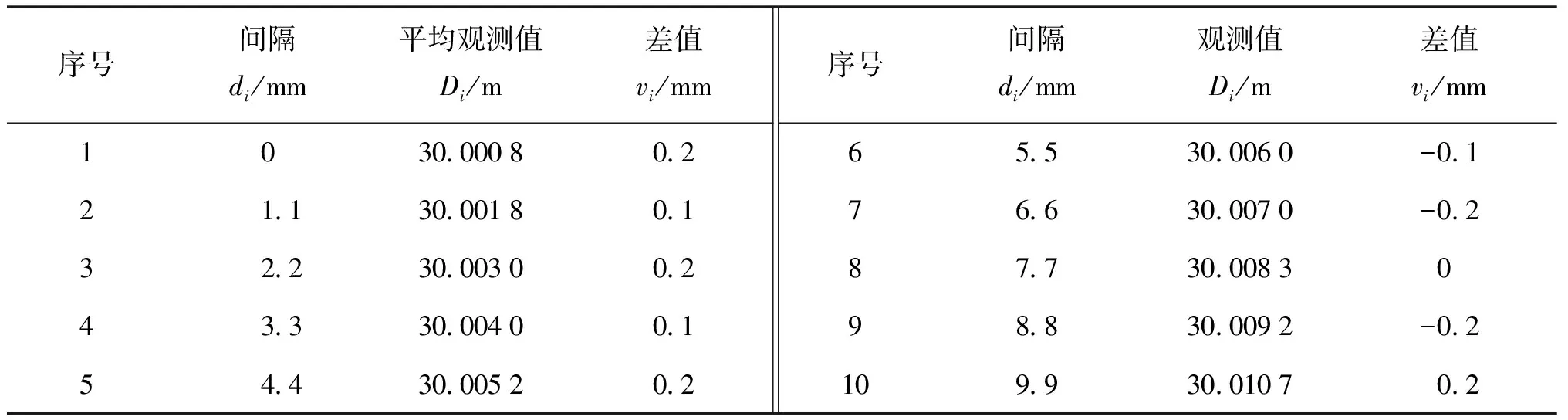
表2 分辨力检定数据Tab.2 Resolution verification data

由《光电测距仪检定规程》给出的公式:

(15)

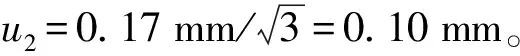
3.3 气象改正引入的测量不确定度

全站仪进行测距工作时,气温(湿温、干温)、气压、大气折射率以及全站仪的载波波长会对距离的测量值有很大影响,因此必须进行气象改正。而由于气象改正与全站仪测距载波波长有关,所以不同品牌全站仪气象改正公式有所不同。徕卡TS06系列载波波长为658 nm,其出厂说明书提供的气象改正公式为:

(16)

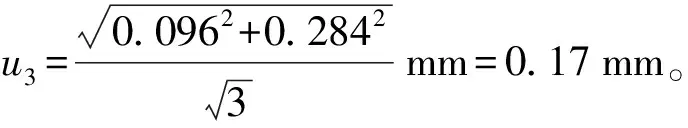
3.4 标准基线标定引入的测量不确定度

检定工作在兰州比长基线场进行,兰州比长基线场最大长度为954 m,最大误差为0.4+1×10-6×D(D为测量距离,m),mm。取其为正态分布,包含因子k=2,则由标准基线标定引入的测量不确定度分量u4=0.68 mm。

3.5 标准基线长度变化引入的测量不确定度

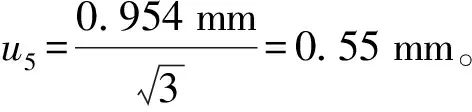
3.6 加常数、乘常数及其标准不确定度计算

根据GUM法不确定度分布传播原理[6]:

则:u(β)=0.91 mm

根据式(4)、式(5)、式(10)、式(11)分别计算加常数、乘常数及其灵敏度系数:

K=-1.1 mm
R=1.4 mm/km
Q11=0.16
Q22=0.49

则由式(12)、式(13)有:

4 MCM法评定不确定度

MCM法在不确定度评定背景下,是一种抽样技术[17～19],以数值的方式而不是解析的方式进行分布与传播。需要得到数学模型输入量的概率密度函数,根据描述输入量的概率密度函数进行重复抽样,根据数学模型以及输入量的概率密度函数得到输出量Y的概率密度函数。由输出量Y的概率密度函数可以得到输出量的所有统计量。

在加常数、乘常数检定中,以式(3)为数学模型,依据第3节分析,输入量L1作为测量重复性引入的误差,取其为半区间长0.4 mm的正态分布;输入量L2作为分辨力引入的误差,取其为半区间长0.17 mm的均匀分布;输入量L3作为气象改正引入的误差,取其为半区间长0.30 mm的均匀分布;输入量D1为基线长度测量引入的误差,取其为半区间长1.36 mm的正态分布;输入量D2作为基线长度变化引入的误差,取其为半区间长0.95 mm的均匀分布。各输入量描述与分布见表3。

表3 蒙特卡洛法输入量评定Tab.3 Monte Carlo method input evaluation

使用Matlab编程进行蒙特卡罗抽样实验[20,21],设定蒙特卡罗实验次数M=106,输出量的概率分布图如图1。

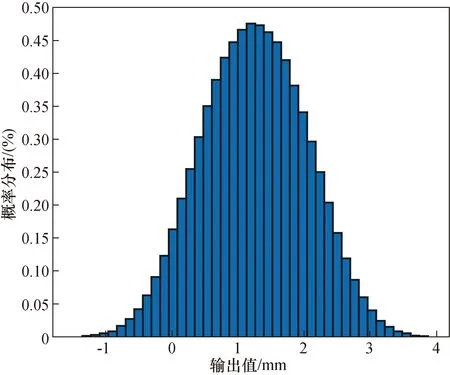
图1 蒙特卡罗试验输出值的概率分布图Fig.1 Probability distribution of Monte Carlo test output value

由图1可知,输出量的概率密度函数可由正态分布或t分布表示,即中心极限定理适用,则可说明该模型可由GUM法评定不确定度。

由蒙特卡罗法得到u(β)=0.79 mm,由式(12)、式(13)可计算加常数、乘常数标准不确定度为

5 两种评定方法比较分析

1) 将两种评定方法得到的结果进行比较得到表4。

表4 两种方法评定不确定度结果

由表4可知,2种方法评定的结果都符合《光电测距仪检定规程》的要求[6]:“加常数、乘常数测量的标准差不大于该仪器标称标准差的1/2”,从不确定度角度即标准不确定度不大于仪器标称标准差的1/2,可以判断本次全站仪加常数、乘常数检定项目结果合格。且2种方法所得结果基本吻合,因此2种方法在进行加常数、乘常数不确定度评价时都是可以采用的。

2) 评定过程中发现,GUM法中当不确定度分量呈正态分布时,依靠实际工作经验选择不同的包含因子与置信概率,对最后结果的评定有较大影响,所以需要根据不确定度分量的相关信息选择合适的置信概率。

3) MCM法是通过数值进行传递,最后结果是基于输出量的概率密度函数的统计量得出的,因此在计算重复性示值产生的不确定度时,理论依据更为充分,所得结果更为精确。

4) GUM法有适用条件,需满足数学模型非线性化不显著,输出量概率密度函数为正态分布或t分布。当适用条件不满足或不知道时,使用GUM法所得结果是不可靠的;MCM法可以得到输出量的概率分布与标准不确定度,则可用来说明GUM法的适用性与结果的可靠性。