时标上高阶神经网络的同步
2023-10-31陈秋媛宾红华黄振坤
陈秋媛,宾红华,黄振坤
(集美大学理学院,福建 厦门 361021)
0 引言
众所周知,同步在安全通信、人工智能和图像处理等[1-10]的实际应用非常广泛。近年来,越来越多的学者研究神经网络的同步问题,如投影同步[1]、滞后同步[2]、量化同步[3]、自同步[6]和指数同步[7]等。
高阶神经网络作为低阶神经网络的扩展,比低阶神经网络具有更强的收敛性和更大的存储容量,因而成为一个新的研究热点。高阶神经网络包括高阶中立型细胞神经网络、高阶Cohen-Grossberg神经网络、高阶Hopfield神经网络和高阶递归神经网络等[6-20]。Hopfield神经网络[9-10]最先由Hopfield提出,它基于由电容、电阻和放大器组成的模拟电路,建立了一个常微分方程组。文献[8]提出了一种具有线性项和间断项的新型控制方案,解决了时变时滞记忆型高阶竞争神经网络的同步问题。文献[16]研究了一类双向联想记忆高阶神经网络的有限时间稳定和固定时间稳定问题。特别地,文献[12]分析了脉冲高阶Hopfield神经网络稳定性,通过构造李雅普诺夫函数和应用线性矩阵不等式,给出了平衡点达到全局渐近稳定的充分条件。
许多关于微分方程的结果很容易转化为差分方程的相应结果,而这些结果与连续的结果在性质上完全不同。时标是研究连续系统和离散系统的有效手段,对时标上的动力学方程的研究揭示了这种差异,并有助于避免对微分方程和差分方程的结果进行两次证明。上述文献大都在连续系统上研究高阶神经网络的稳定性,对离散系统的关注较少。因此,在时标理论基础上研究高阶神经网络的同步问题很有必要。经过多年的研究,Hilger提出的时标理论已经取得了很多成果[21-24],但时标上高阶神经网络的同步尚未得到研究。因此,本文在文献[12]和时标微积分理论的基础上,讨论时标上高阶神经网络驱动-响应系统在脉冲控制下达到同步的充分条件,为时标上高阶神经网络的同步研究提供了理论基础。
1 预备知识
时标T为实数集R的任意非空闭子集,其拓扑结构继承自R。时标上的跳跃算子σ(t)和ρ(t)的定义分别为:σ(t)=inf{s∈T:s>t},ρ(t)=sup{s∈T:s
定义1[24]给定函数f:T→R且t∈Tk。对任意ε>0,若存在f△(t),对于t的某个邻域U,使得|f(σ(t))-f(s)-f△(t)(σ(t)-s)|≤ε|σ(t)-s|,∀s∈U,那么称它为f在t处的△-导数。
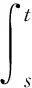
引理1[24]若f和g是两个在时标T上△可导的函数,则:i)(f±g)△(t)=f△(t)±g△(t);ii)(fg)△(t)=f△(t)g(t)+f(σ(t))g△(t)=g△(t)f(t)+g(σ(t))f△(t)。若f在t点可导,则f(σ(t))=f(t)+μ(t)f△(t)。
引理2[24]对于p,q∈R,有:i)ep(σ(t),s)=(1+μ(t)p(t))ep(t,s);ii)ep(t,s)ep(s,r)=ep(t,r);iii)若p∈R+,则ep(t,t0)>0,∀t∈T。
引理3[24]设y∈Crd,且p∈R+,若y△(t)≤p(t)y(t),t∈T成立,则y(t)≤y(t0)ep(t,t0)。
2 模型描述
考虑由n个节点构成的高阶神经网络,其驱动系统为
(1)
其中:i=1,2,…,n;t∈T;xi(t)是时间t第i个神经元的状态量;gi(xi(t))和hi(xi(t))是神经激活函数;Ci>0和Ii分别表示第i个节点的自反馈权重和外部输入量;Aij、Wij和Aijl、Wijl分别表示神经网络的一阶和二阶神经元的权重。
对应的响应系统为
(2)
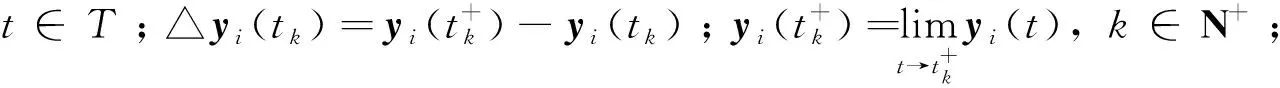
假设1 假定系统(1)的神经激活函数gi(xi)和hi(xi)(i=1,2,…,n)是连续的,且满足以下条件,即
(3)
设ei(t)=yi(t)-xi(t),i=1,2,…,n,可得
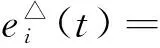
gj(xj(t))gl(xl(t))-gj(yj(t))gl(xl(t))+gj(yj(t))gl(xl(t))]}=-Ciei(t)+
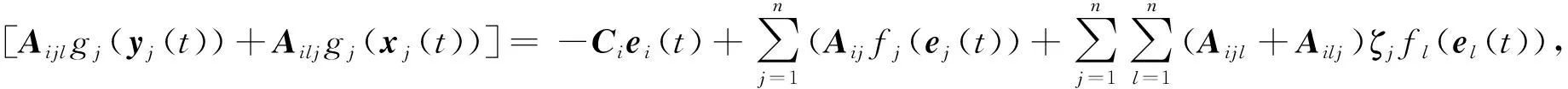
故系统(1)和(2)的误差系统为
(4)
其中:i=1,2,…,n;t∈T;fi(ei(t))=fi(gi(t))-gi(xi(t));φi(ei(t))=hi(yi(t))-hi(xi(t));ζj介于gj(xj(t))和gj(yj(t))之间;ξj介于hj(xj(t))和hj(yj(t))之间。
注1 根据函数的凸性和Aijl/(Aijl+Ailj)+Ailj/(Aijl+Ailj)=1,存在ζj介于gj(xj(t))和gj(yj(t))之间,使得Aijlgj(xj(t))+Ailjgj(yj(t))=(Aijl+Ailj)ζj成立。
相应地,假设1可改写成:
(5)
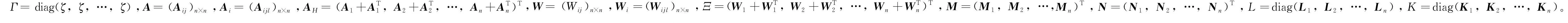
(6)
这里,对于矩阵P,λmin(P)和λmax(P)分别表示方阵P的最小和最大特征值。范数‖·‖是欧几里得范数,e表示单位矩阵。
3 主要结果
定理1 在假设1的条件下,如果
(7)
证明构造Lyapunov函数为V(t)=eT(t)e(t)/2。利用引理1得:V△(t)=[eT△(t)e(t)+eT(σ(t))e△(t)]/2=[eT(t)+eT(σ(t))]e△(t)/2=[2eT(t)+μ(t)eT△(t)]e△(t)/2=eT(t)e△(t)+μ(t)eT△(t)e△(t)/2。当t∈[tk-1,tk)T(k∈N+)时,对V(t)沿系统(6)的轨道求导。由2uTv≤uTu+vTv、ΓTΓ≤‖ζ‖2I和‖ζ‖≤‖M‖可得
eT(t)e△(t)=eT(t)(-Ce(t)+Af(e(t))+FT(e(t))AHζ)=-eT(t)Ce(t)+eT(t)Af(e(t))+
eT(t)FT(e(t))AHζ≤-eT(t)Ce(t)+eT(t)AKe(t)+eT(t)ΓTAHf(e(t))≤-eT(t)Ce(t)+
eT(t)(AK+KAT)e(t)/2+eT(t)ΓTΓe(t)/2+fT(e(t))ATAHf(e(t))/2≤-eT(t)Ce(t)+
eT(t)(AK+KAT)e(t)/2+‖M‖2eT(t)e(t)/2+eT(t)KATAHKe(t)/2=eT(t)(-2C+AK+KAT+
(8)
且有
eT(t)C2e(t)-eT(t)CAf(e(t))-eT(t)CFT(e(t))AHζ-fT(e(t))ATCe(t)+fT(e(t))ATAf(e(t))+
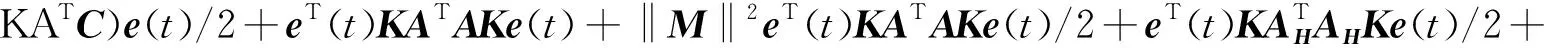
(3/2+‖M‖2/2)KATAK]e(t)≤λmax[(1+‖M‖2)C2-(CAK+KATC)+(3/2+
(9)
于是有
(10)
因此,由式(8)和式(10)有
(11)
(12)
当t=tk(k∈N+)时,有
ΦT(e(tk))Ξξ]/2≤eT(tk)[(1+‖N‖2)(E+D)2+LWT(E+D)+(E+D)WL+(3/2+
3/2‖N‖2)LΞTΞL+(3/2+‖N‖2/2)LWTWL]e(tk)/2≤λmax[(1+‖N‖2)(E+D)2+LWT(E+D)
+(E+D)WL+(3/2+3/2‖N‖2)LΞTΞL+(3/2+‖N‖2/2)LWTWL]V(tk)=V(tk)。
(13)
由引理2、式(12)~式(13)有
(14)
所以,V(t)≤Nγ(t0,t)eλ(t,t0)V(t)。因为Nγ(t0,t)eλ(t,t0)=0,故系统(1)和(2)在脉冲控制下达到同步。
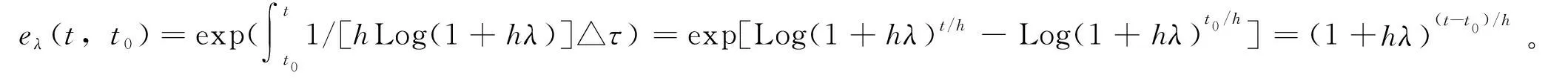
注2hZ不仅包含普通的差分方程形式(h=1),也包含非特殊的差分形式(h≠1)。当h=1时,系统(1)可改写成
本文可以得到类似定理1的结果,此结果是对文献[15]的补充。文献[15]研究了具有时滞和脉冲的离散高阶神经网络的稳定性。文献[17]提出了时标上一类中立型高阶Hopfield神经网络,讨论其概周期解的全局指数稳定性。不同的是,本文加入脉冲控制器来研究时标上高阶神经网络的同步,结果更具一般性。当T=R时,可以参考文献[12]在连续情形上研究脉冲高阶Hopfield型神经网络的稳定性。
4 数据模拟结果
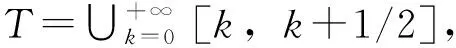
考虑高阶神经网络
(15)
和
(16)
其中:i=1,2,3;g1(z)=tanh(0.16z);g2(z)=tanh(0.14z);g3(z)=tanh(0.16z);h1(z)=tanh(0.2z);h2(z)=tanh(0.6z);h3(z)=tanh(0.5z);C=diag(1.6,1.5,1.3);D=diag(-0.21,-0.78,-0.69);
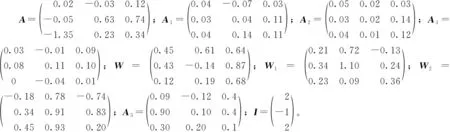
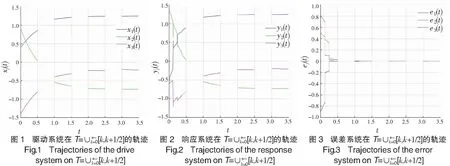
注3 上述例子是在混合时域下进行数值模拟,包含了离散和连续的结果。
