无界区域上分数阶 Klein-Gordon 方程的近似人工边界条件
2023-10-31朱荣坤梁宗旗
朱荣坤,梁宗旗
(集美大学理学院,福建 厦门 361021)
0 引言
分数阶微积分是现代数学理论和应用研究的一个新的重要分支,它不仅是传统整数阶微积分理论的推广,同时由于分数阶微分算子的非局部性,分数阶微分方程非常适合用来描述现实世界中具有记忆和遗传性质的材料,以及许多物理及动态系统过程,从而分数阶微分方程在科学与工程的各个领域得到了广泛的应用,如光学、流体力学、化学、物理学、金融和其他自然科学[1-4]。分数阶微分方程理论研究和数值计算方法[5-6]是当今国内外学术界的最热门的研究课题之一。出现在科学和工程领域中的大量问题都是建立在无界区域上的,最终大部分可归结为无界区域上分数阶微分方程,如流体在无限长管道中的流动、波在空间中的传播等。然而物理区域的无界性和分数阶微积分算子的非局部性,给无界区域上问题尤其分数阶微分方程的求解带来了本质性的困难和巨大的计算代价。如何设置人工边界并高效求解成为求解无界区域上偏微分方程和分数阶微分方程数值解的一个核心问题,人工边界方法已逐步发展成为数值求解无界区域上偏微分方程的一个重要且高效方法,在科学技术的众多领域中得到了广泛应用。
关于整数阶偏微分方程人工边界方法的研究,人们针对不同方程和物理区域的人工边界应用多种方法和技巧进行了大量研究,Han等[7]应用Laplace变换得到了热传导方程的精确人工边界条件;有文献给出了二维Laplace方程外问题的一系列各种精度的局部人工边界条件[8]、非线性KdV方程的透明人工边界条件[9]、一维三次非线性Schrödinger方程的精确非线性人工边界条件[10]等。关于分数阶微分方程的人工边界条件的研究文献很少,主要的原因是对整数阶微分方程人工边界条件本身需要较高的构造技巧和理论分析,即使是简单的线性微分方程构造,其人工边界条件也是困难的。分数阶微分方程不仅具有全局性,而且分数阶导数还存在奇异性,所以对无界区域上求得分数阶微分方程的精确人工边界条件或近似人工边界条件是困难的。Gao等[11]研究了无界区域上时间分数阶次扩散方程的精确人工边界条件;Zhang等[12]利用降阶法研究了无界区域上时间分数阶线性KdV方程的人工边界条件,得到了其精确人工边界条件。为了克服物理区域的无界性、分数阶导数的非局部性,减少计算代价,本文提出了一种利用人工边界方法[11,13-15]和Lagrange插值[16]求解无界区域上分数阶偏微分方程的新的方法,可将无界区域分数阶微分方程近似转化为有界区域上人工边界条件下整数阶偏微分方程的初边值问题,从而达到计算代价小、简单、高效的目的。
本文主要研究如下的无界区域上时间分数阶Klein-Gordon方程为
(1)
u(x,0)=φ(x),ut(x,0)=ψ(x),x∈R,
(2)
u(x,t)→0,|x|→∞,t∈(0,T]。
(3)

1 人工边界方法
1.1 预备知识
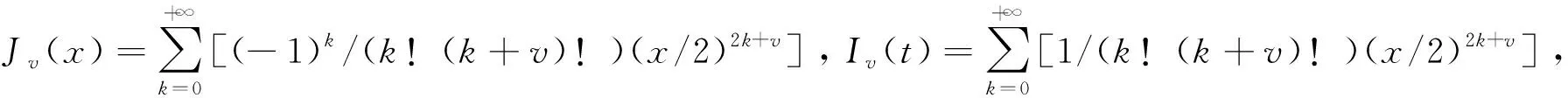
引理2I0、I1分别为0阶和1阶广义的Bessel函数,则有I0′(x)=I1(x)。
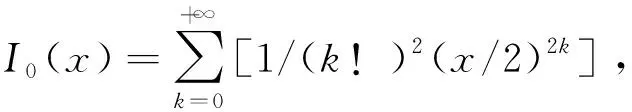
引理3Iv为v(v≥1)阶广义的Bessel函数,则有递推式2Iv′(x)=Iv-1(x)+Iv+1(x)。
1.2 人工边界条件
Caputo分数阶导数的非局部性,导致当前时间层的计算需要存储之前所有时间层的数据,这给分数阶导数的计算带来了巨大的存储代价。为了克服这一困难,对Caputo分数阶导数做Laplace变换,可得
(4)
对sα做Lagrange线性插值逼近,可得
sα≈(α-1)s2+(2-α)s。
(5)
将式(5)代入式(4)式中,可得
(6)
对式(6)做Laplace逆变换,可得
(7)
将式(7)代入方程(1)中,得到问题(1)~(3)的近似问题为
(8)
其中g(x,t)=(2-α)ψ(x)+f(x,t)。
现引入人工边界∑r={(x,t)|x=xr},∑l={(x,t)|x=xl},人工边界∑r、∑l将无界区域R=(-∞,+∞)分割为Ωi=[xl,xr]和Ωe=(-∞,xl)∪(xr,+∞)两部分。
考虑无界区域上Ωe问题(8)的外问题
(9)
对方程(9)做Laplace变换,得到如下的常微分方程为
求解以上常微分得其解为
(10)
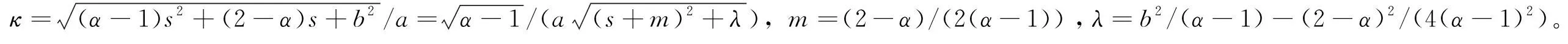
式(10)等价于
(11)
当λ满足不同的条件时,式(11)会得到所对应的人工边界条件,因此分3类情况讨论。
情况1 当λ=0,即b2=(2-α)2/(4(α-1))时,式(11)可写为
(12)
对式(12)做Laplace逆变换,可得
即
从而,当λ=0时,得到与问题(1)~(3)等价的人工边界条件下的初边值问题为:
(13)
情况2 当λ>0,即b2>(2-α)2/(4(α-1))时,式(11)可写为:
(14)
当x∈(xr,+∞)时,式(14)等价于
(15)
对式(15)做Laplace逆变换,并利用引理1和Laplace逆变换的平移性及分部积分,得到:
即
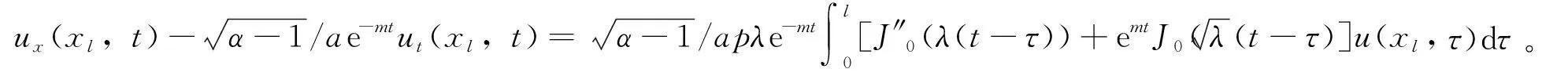
(16)
情况3 当λ<0,即b2<(2-α)2/(4(α-1))时,式(11)可写为
(17)
即
(18)
对式(18)做Laplace逆变换,并利用引理1和Laplace逆变换的平移性,同理得到
(19)
利用引理2、引理3和分部积分,式(19)可写为
同理得到当x=xl时的人工边界条件,当λ<0时,从而得到与方程(1)~(3)等价的人工边界条件的初边值问题为
(20)
根据λ的正负,本节给出了无界区域上时间分数阶Klein-Gordon方程(1)~(3)3类情况下的人工边界条件。不失一般性,本文只研究人工边界条件下初边值问题(20)的稳定性。
2 稳定性分析
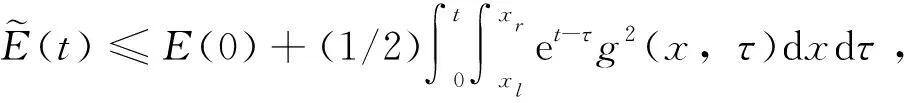
证明用ut(x,t)乘以方程组(20)的第一个式子,在[xl,xr]上积分,并利用式(20)的二、三个式子,得到
即
(21)
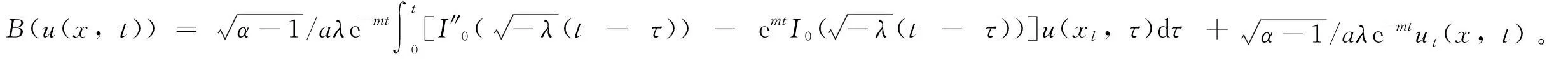
(22)
(23)
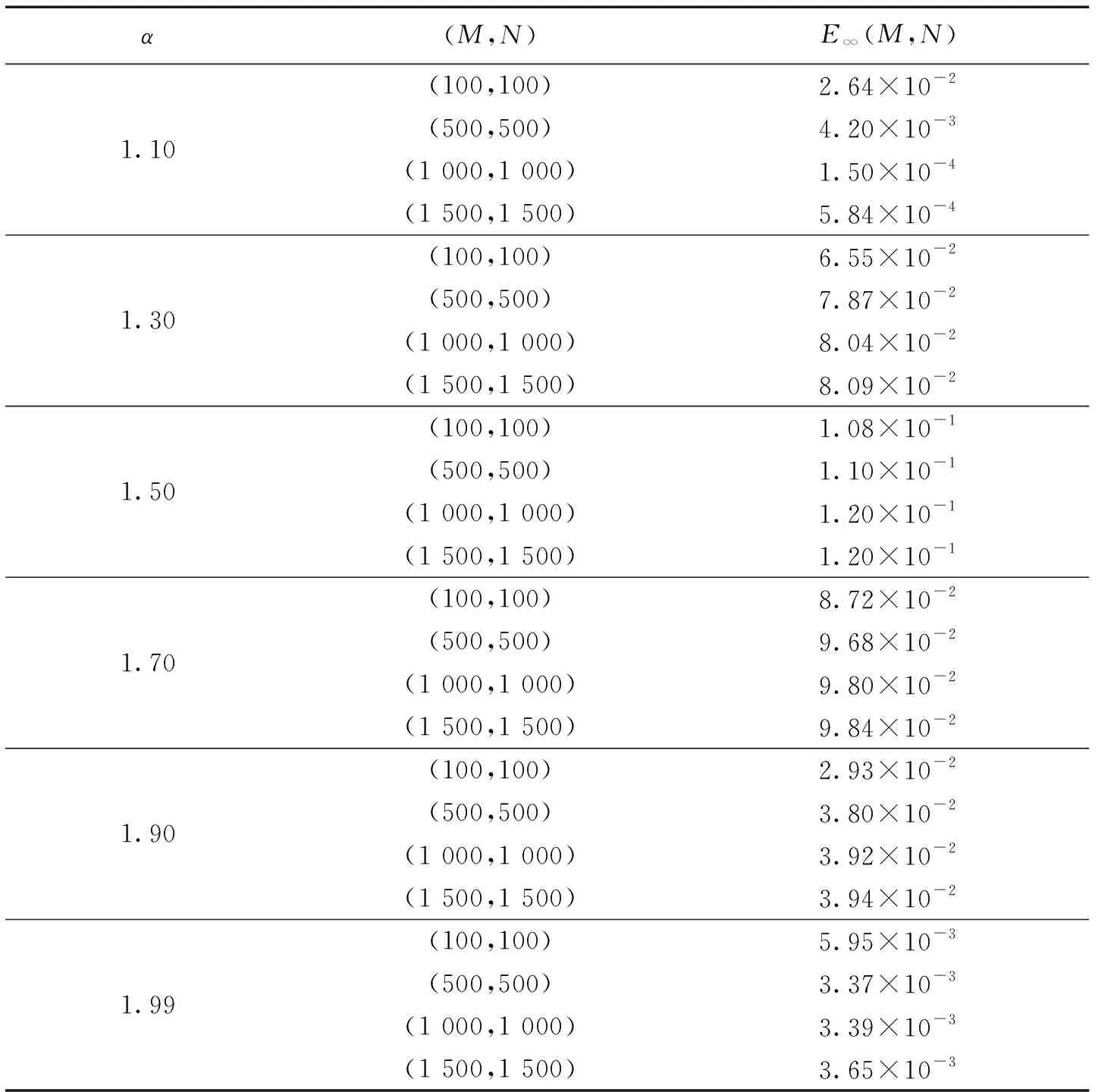
其中:Dr={(x,t)|1≤x<∞,0≤t≤T};Dl={(x,t)|-∞≤x 用w(1)(x,t)、w(2)(x,t)分别乘以式(22)和式(23),在[xr,+∞),(-∞,xl]上积分,并利用式(20)的第二、三个式子,得到 (24) (25) 将式(24)和式(25)代入式(21),得到 (26) 令 (27) (28) 为了验证利用Laplace变换与人工边界方法来求解无界区域上时间分数阶Klein-Gordon方程的有效性,本节仅对问题(13)做数值离散和模拟。 记Λ:=[xl,xr],I=[0,T],Ω=Λ×I,将求解区域Ω={(x,t)|xl≤x≤xr,0≤t≤T}进行网格剖分。取正整数M、N,令h=(xr-xl)/M,τ=T/N,xi=x0+ih(0≤i≤M),tk=kτ(0≤k≤N),其中,h是空间步长,τ为时间步长。 引理4[15]设y(x)∈C3[xl,xr],其中xl=x0,xr=xM,则有:y″(x0)-2[(y(x1)-y(x0))/h-y′(x0)]/h=-h/3y‴(x0+θ1h),θ1∈(0,1);y″(xM)-2[(y′(xM)-y(xM-1))/h]/h=-h/3y‴(xM-θ2h),θ2∈(0,1)。 利用中心差分格式分别逼近时间空间二阶导数,蛙跳格式逼近时间二阶导数,并结合引理4将问题(13)离散成 (29) 本节将通过数值例子来验证有限差分格式(28)的有效性。 表1 不同时间空间步长下的最大误差Tab.1 The maximum errors with different temporal and spatial nodes 利用Laplace变换和Lagrange插值方法,首先将分数阶微分方程转化为近似整数阶微分方程,再利用人工边界方法,将无界区域上时间分数阶Klein-Gordon方程转化为有界区域上具有精确人工边界条件的整数阶偏微分方程问题,同时证明了其稳定性。最后,构造了人工边界条件下整数阶偏微分方程的有限差分格式,并利用数值例子验证格式的有效性。该方法为无界区域上分数阶偏微分方程问题的求解提供了一种新的理论方法,不仅降低了计算代价,而且简化了原问题,说明利用人工边界方法求解无界区域上分数阶微分方程是一个简单、有效的方法。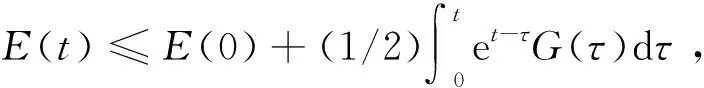
3 有限差分格式与数值模拟
3.1 有限差分格式

3.2 数值模拟
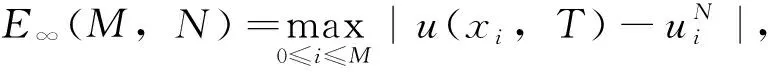
4 结论
