基于Dubins曲线的AUV集群协同搜索优化
2023-10-31刘佳宁
刘佳宁,郑 凯,梁 霄
(1. 大连海事大学船舶电气工程学院,辽宁 大连 116026;2. 大连海事大学船舶与海洋工程学院,辽宁 大连 116026)
0 引言
近年来,随着国家海洋强国战略的实施,人们对海洋领域的探索、开发越来越深入。自主式水下航行器(autonomous underwater vehicle,AUV)作为一种有效的海洋勘探装置,可以执行多种复杂任务,如资源勘探、海上救捞[1]、沉船勘探[2]等。但是,在参与韩国“世越号”客船打捞、马航MH370航班搜索、泰国普吉岛客船救援等事故过程中,由于AUV自身携带能源有限,单个AUV已不能满足大规模海洋搜索应用的需求[3]。多AUV以集群的形式开展工作,可以扩展单个AUV的感知范围,提高探测效率,目前已经成为研究的热点[4]。
目前,国内外对区域全覆盖搜索的路径规划进行了大量的研究,相关算法主要包括随机法[5]、内螺旋式[6]、循环往复式[7]等。由于AUV受运动学约束及自身转弯半径的限制,并不能直接应用陆地机器人的相关算法。乔昶超等[8]介绍了单个AUV在矩形区域内执行探测水雷任务,采用牛耕式(即循环往复式)搜索算法,并进行仿真研究。王琦斐等[9]提出多AUV构成的集群,采用内螺旋式覆盖搜索方法,在接近中心区域时AUV需要执行大量的转弯动作,实现过程较为复杂。张跟鹏等[10]分析了UUV集群采用不同的探测模式在搜索时间、效能等方面的区别,其中包括单UUV的梳状搜索、UUV集群的平行协同式搜索和交叉式搜索等。Chen等[11]对牛耕式搜索算法进行相关改进,通过调整集群中AUV的转弯时机,使集群的重复搜索区域变小,同时通过设置相邻两个搜索区域之间的重叠率,来实现对目标区域的全覆盖搜索。郝燕玲等[12]使用遗传算法在静态环境下实现AUV的三维全局路径规划。Sipahioglu等[13]将传感器探测范围与路径规划算法相融合,生成一条全覆盖路径。Wen等[14]将蚁群算法与生物激励神经网络相结合,提出了一种全覆盖路径规划算法。但上述算法中均未考虑AUV的运动学约束问题。
Dubins[15]考虑到机器人转弯半径的影响,利用几何方法求解了机器人初始状态与结束状态之间的最短路径问题。张骁等[16]和胡蔷等[17]分别将Dubins曲线加入到A*算法、遗传算法中,当AUV在航行过程中遇到障碍物时,生成的最终路径能够避开障碍物并且满足AUV的运动学约束,进而使AUV集群的路径满足约束条件。
针对大范围开阔海域的目标搜索问题,采用牛耕式搜索法[18]可覆盖大部分目标搜索区域。由于AUV转弯过程受自身转弯半径约束,在转弯的相反方向会存在遗漏的搜索区域,随着AUV转弯次数的增多,遗漏区域的面积会逐渐增加,因此使用牛耕式搜索方法无法实现目标区域的全覆盖搜索,并且集群中邻近两个AUV之间存在大量的重复搜索区域,造成资源浪费。针对该问题,Chen等[11]通过设置邻近两个AUV之间搜索区域的重叠率,来实现全覆盖搜索,然而该方法会增加AUV集群的总体搜索时间,不适合任务初期的目标搜索。
本文在文献[11]的基础上,提出一种新型协同搜索算法,在外侧路径中融合Dubins曲线特征进行路径规划,调整集群中不同位置AUV的转弯时机,减少重复探测区域,使得AUV集群在实现全覆盖的条件下重复搜索面积最小。
1 问题描述
本文主要针对开阔海域,使用多个相同类型的AUV,以集群形式执行搜索任务这一问题。设搜索海域为S,面积为Lx×Ly,其中Lx表示区域长度,Ly表示区域宽度。海域内目标的位置、数量等信息均未知。共使用n个AUV构建集群,每个AUV上均搭载相同的探测设备,传感器探测区域为一个Rx×Ry的矩形,在AUV航行的正前方,Rx和Ry分别为相对于AUV的横向和纵向距离,且Rx≥2Ry。AUV的速度为恒定值V,最小转弯半径为RL。AUV集群对该区域搜索的场景,如图1所示。
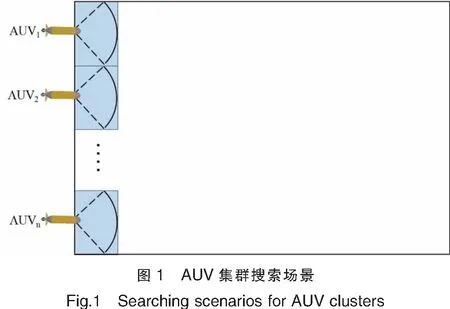
设第i个AUV在整个区域搜索过程中的扫描范围为Si,则AUV集群搜索范围Sall为:
Sall=S1∪S2∪S3∪…∪Sn。
(1)
AUV集群对目标区域实现全覆盖搜索时应满足
S⊆Sall。
(2)
针对上述问题做出如下假设:
1)若整个搜索区域S的长度Lx、宽度Ly,均大于AUV集群的探测宽度nRx,即AUV集群不能不经历转弯就完成对目标区域S的搜索;反之,AUV集群组成一排横队直线航行即可完成目标区域的全覆盖搜索。
2)AUV搭载的传感器探测宽度Rx大于其自身的最小转弯半径RL,在AUV转弯过程中需要执行一段直线航行。
3)AUV集群始终航行在目标物的上方,因此,在搜索过程中AUV集群航行深度保持不变即可完成目标区域的探测任务,故集群航行的区域可以看作一个二维平面。
2 集群搜索方案
多AUV以集群的形式协同执行搜索任务时,为尽快搜索目标物,减少搜索时间,需要明确集群的起始搜索方向及集群内部的队形。
2.1 确定起始搜索方向
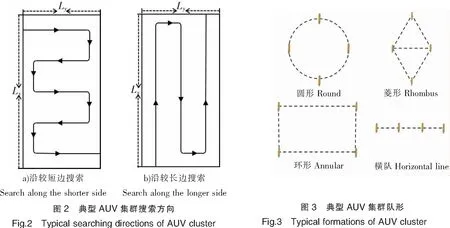
AUV在运动过程中,由于其转弯半径的影响,转弯航行比直线航行需要消耗更多的能源和时间,因此,在集群搜索过程中应尽可能减少转弯航行。单AUV根据起始搜索方向的不同,最终的搜索轨迹差距很大,如图2所示。图2a为起始搜索方向平行于搜索区域的较短边Ly,搜索整个区域,共转弯8次;图2b的起始搜索方向平行于搜索区域的较长边Lx,共转弯4次。因此为减少AUV路径中的转弯次数,AUV集群的起始搜索方向应平行于搜索区域的较长边。
2.2 确定集群队形
AUV集群中常见的编队队形有以下几种:圆形队形、菱形队形、环形队形、横队队形等[19-20],如图3所示。针对本问题,规划时应使用最少数量的AUV,尽可能实现最大的搜索范围。横队队形相较于其他的队形,航行过程中重复搜索区域最小,能最大展现该AUV集群的搜索能力,因此选用横队队形来进行搜索。
3 基于Dubins曲线的改进搜索
3.1 传统牛耕式搜索
AUV集群采用横队队形来进行搜索,常见的方式即牛耕式,如图4所示。图4中三种不同颜色的线条分别代表不同AUV的规划路线,箭头方向代表AUV的运动方向,蓝色矩形代表AUV在当前位置的搜索区域。当AUV航行至区域最右侧时,分别以最小转弯半径向右侧转弯,待恢复至垂直方向之后继续向前直线航行。当驶离已经搜索过的区域后,AUV分别向右侧转弯恢复至水平方向,直至将目标区域搜索完毕。
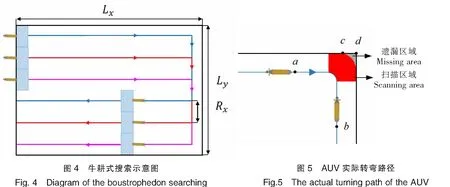
使用该搜索方式时,当AUV集群到达最右侧边界之后开始转弯,此时由于受转弯半径及运动学约束的影响,AUV实际并不能按照规划的预定路线进行直角转弯,而是以合适的转弯半径来改变方向,即转弯过程航行的路线为圆弧状。如图5所示,AUV由a点航行至b点,图5中红色扇形区域为AUV在实际转弯过程中扫描区域的左侧部分,而从点c开始出现灰色的遗漏区域,并且在转弯之后的航行过程中存在大量的重复搜索区域。线段cd的长度Rcd为:
Rcd=Rx/2+RL-Ry。
其中Rx、Ry分别为传感器的水平探测距离与垂直探测距离。由此得Rcd大于0,因此该遗漏区域一直存在,且AUV每次转弯过程均会产生一个相同大小的遗漏区域。当AUV集群搜索的目标物位于这些遗漏区域中时,无论AUV集群如何搜索,均无法将目标物探测到。假设最坏的情况,所有的目标物均散落在这些遗漏区域中,则AUV集群的搜索成功率为0,搜索任务失败。该集群搜索方式并没有实现对目标区域的全覆盖搜索,此时AUV集群搜索区域Sall与目标区域S之间的关系为:
SallS。
3.2 基于Dubins曲线优化搜索方式
对于上述传统牛耕式搜索最外侧AUV转弯过程产生的遗漏区域,需对该搜索路径进行相关改进。Dubins曲线由直线段与最大曲率弧线段组成,两段圆弧线满足最小转弯半径的约束,直线为连接两段圆弧航线的公共切线,常用于解决满足曲率约束且带有方向的起始位置与终止位置之间的最短路径问题,主要应用于运动体的轨迹规划,因此将Dubins曲线融入到AUV的转弯轨迹中求解上述问题。典型的Dubins曲线有以下四种:LSR、RSL、RSR、LSL。其中:L代表逆时针向左旋转;R代表顺时针向右旋转[15](见图6)。
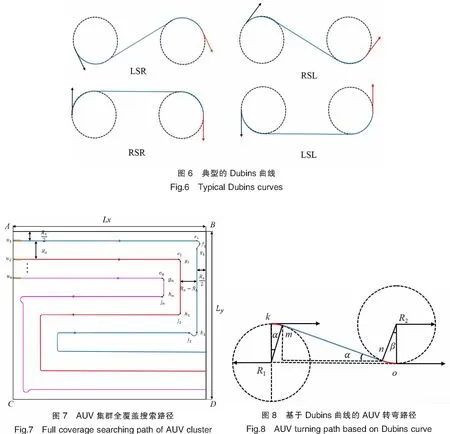
以n艘AUV构成集群为例,假设矩形ABCD为搜索区域S,对该区域进行全覆盖搜索,如图7所示。图7中蓝色、红色、紫色线条分别代表3艘AUV的航行路径。具体路径为:
1)整个搜索区域为S,其中Lx大于Ly,因此以AC边作为AUV集群的起始边界,起始航行方向为水平向右,集群内AUV采取横队队形。AC边上的点u1,u2,…,un作为AUV集群的起始位置,其中AUV1与A点之间的距离为Rx/2,集群内部相邻两个AUV之间的间隔同样为Rx。
2)AUVn的unen段路径相较于其他AUV的航线最短,因此其最先到达en点,之后以最小转弯半径RL向右转弯,执行en至jn段路径,其中gnhn段直线航行距离为Rx-2RL。同理,集群中各个AUV到达各自的e点之后,除AUV1外第i个AUV的eigi段直线距离为(n-1)Rx+Rx-2RL。
3)当AUV1航行到距离右侧边界Ry的e1点时,AUV1开始以最小转弯半径RL向右转弯,转弯角度为90°,此时AUV1到达f1点,运动方向为平行线段BD向下,但此时AUV1的搜索范围已经超出目标区域,即当前搜索存在部分的无效区域,且AUV2转弯过程会存在遗漏区域,因此需要使AUV1的航线恢复至距离BD边界Rx/2处,且运动方向为平行BD向下,进而来弥补AUV2搜索的遗漏区域。
此时起始点与终止点的位置、方向均已知,在路径中结合Dubins曲线中的RSL,如图8所示,假设起始R1与结束R2两个圆半径分别为AUV的最小转弯半径RL和RL2。
图8中,k点为AUV1的当前位置,对应AUV的运动方向应水平向右,为Dubins曲线的起始点;假设O点为AUV1恢复至距右侧边界Rx/2处,方向与点k相同,则该点为终止点。在k点到O点的路径中加入Dubins曲线,整段曲线L由R1圆上的红色弧线L1,R2圆上的红色弧线L3,以及两个圆R1、R2之间的切线L2组成。L1、L3分别为AUV绕其转弯半径旋转α°、β°航行的路径,则
L=L1+L2+L3。
其中:
L1=αRL(0°≤α≤60°);
L2=((RL+RL2-(RL2/cosα))/tanα);
L3=βRL2(α=β);
RL2≥RL。
那么k点至O点之间的水平距离
Lko=((RL+RL2)cosα-RL2/tanα))+(RL+RL2)sinα。
该段路径在规划时应使整段曲线L尽可能小,即RL2=RLcosα/(1-cosα)取极值时。
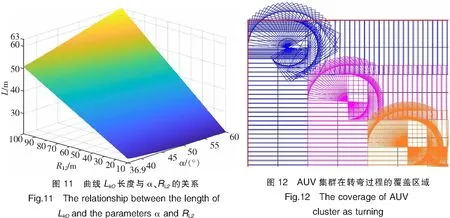
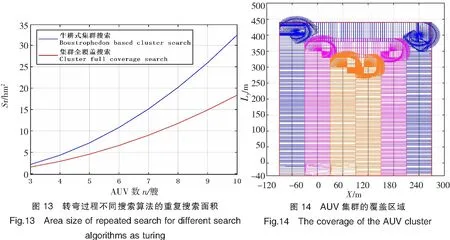
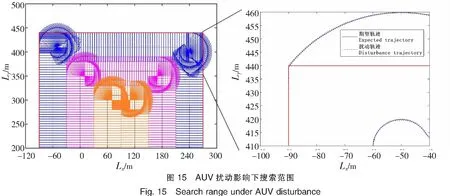
根据实际情况,与AUV1邻近的AUV2在转弯过程中同样会产生一个相同的遗漏区域,因此,为实现全覆盖搜索,应对LkO长度加入以下限制,即O点应在AUV2搜索范围的左侧:LkO 4)AUV1到达g1点之后,沿线段g1h1航行。如图9所示,AUV1在g1点时搜索范围超过c点,此时AUV1将AUV2的转弯过程的遗漏区域覆盖,满足局部的全覆盖要求,相邻两个AUV之间的距离为Rx/2-RL,且AUV集群又重新恢复至横队队形。 5)之后AUV集群重复步骤1)~4),AUV集群在每次转弯的过程中,最外侧AUV按照改进之后的预定路线航行,内侧AUV均按照最小转弯半径转弯,直到完成目标区域的全覆盖搜索。 针对上述设计的AUV集群全覆盖搜索路径,在Matlab R2018b环境下进行仿真验证,整个搜索区域S大小为360 m×480 m。AUV的最小转弯半径RL=10 m,传感器水平探测距离Rx=60m,垂直探测距离Ry=30 m,则设计的路线中水平距离LkO与AUV转弯过程的旋转角度α和圆R2的最小转弯半径RL2之间的关系如图10所示。根据上述条件,在实现全覆盖的前提下,要使重复搜索区域最小,LkO应小于20 m,在RL2=RL的情况下,旋转角度α最小取36.9°。 路径中Dubins曲线L的长度与旋转角度α、圆R2转弯半径RL2的关系,如图11所示。在航行过程中,应尽可能使路径最短,根据L取最值时RL2与角度α之间的关系,求解得当角度α为60°、RL2取10 m时,Dubins曲线L达到最小长度20.944 m。 根据上述所求旋转角度α,使用3艘AUV构成集群对目标区域进行搜索,搜索区域的四个顶点坐标分别为:(-90,40)、(-90,440)、(270,440)、(270,-40)。AUV集群的初始坐标为:(-60,-40)、(0,-40)、(60,-40)。 AUV集群根据上述规划的路径对目标区域执行搜索任务,其中AUV1在转弯过程的搜索区域,如图12所示。从图12中可以看到AUV1转弯航行过程的搜索区域将传统牛耕式搜索算法遗漏的区域全部覆盖,同时在转弯之后将AUV2转弯航行产生的遗漏区域同样覆盖,因此,实现了目标区域全覆盖搜索的要求。 使用传统牛耕式路径规划算法对集群搜索路线进行规划时,在集群到达区域最右侧后,多艘AUV重复航行一段直线区域,在该段直线路径中,每艘AUV搜索区域为(n-1)Rx2。基于Dubins曲线的集群协同全覆盖搜索算法仅在相邻两艘AUV之间存在重复搜索区域,则重复搜索区域面积为: 根据最初假设Rx>RL,当n(2≤n≤10)艘AUV构成集群时,两种集群搜索算法的重复搜索面积,如图13所示。图13中横轴表示集群中AUV的个数,纵轴表示一次转弯过程集群中的重复搜索区域面积Sr。由图13可得,本集群搜索算法比传统牛耕式集群搜索算法重复搜索面积更小,且集群中AUV越多,本集群搜索算法在重复搜索方面越占优势。 AUV集群根据上述规划路径搜索目标区域,如图14所示,其中蓝色、紫色、橙色区域分别为3艘AUV实际搜索到的区域,搜索区域内的黑色线条分别为集群中3艘AUV的航行路线。从图14中可以看到,集群中相邻AUV搜索区域之间没有产生遗漏部分,对目标区域实现了全覆盖搜索,该集群协同搜索路径实现了对目标区域的全覆盖搜索,此时AUV集群搜索范围Sall与目标区域S之间的关系为:S⊆Sall。 在实际搜索时,AUV航行会受到外部扰动影响,从而改变AUV的实际航迹。为验证在这种条件下,本文方法仍然有效,图15给出了在扰动影响下AUV在转弯处的覆盖结果。由于受扰动影响,其覆盖边缘出现了一定范围的变化,但图15显示仍可以实现对搜索区域的全覆盖,因此,可以说本文方法对外部扰动也具备一定的鲁棒性。 本文针对开阔海域AUV协同搜索问题提出了一种基于Dubins曲线的集群协同全覆盖搜索算法。本算法首先对集群中不同位置AUV的转弯时机进行了调整,然后融合Dubins曲线到AUV集群的外侧路径规划中,实现了目标区域的全覆盖搜索。通过对协同覆盖算法进行仿真实验,本算法的重复搜索区域较牛耕式搜索算法更少,从而验证了本算法的有效性和优越性。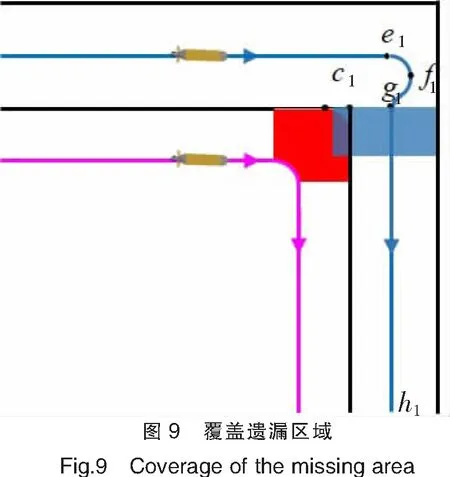
4 仿真实验

5 结论
