基于ReliefF和最大相关最小冗余的多标记特征选择
2023-10-31孙林徐枫李硕王振
孙林,徐枫,李硕,王振
(河南师范大学 计算机与信息工程学院,河南 新乡 453007)
目前,多标记学习是数据挖掘、人工智能等领域的一个重要的研究方向[1].作为数据挖掘的预处理技术,多标记特征选择策略可分为过滤式、封装式和嵌入式[2].过滤式在效率上有一定的优势,而如何构建合适的评价指标来评价候选特征是过滤式的关键,并且不依赖特定分类器,由此选择出来的特征子集对于不同的分类器适用性更强[3].王晨曦等[4]通过融合标记权重与对象平均间隔构建了邻域信息熵,进而设计了信息粒化多标记特征选择模型.但是该方法未涉及标记之间以及特征与标记集之间的相关性.魏葆雅等[5]使用标记对对象的可分性赋予标记权重,并联合特征权重对特征进行排序,基于标记重要性提出了多标记特征选择模型.但是该模型未涉及特征与标记间的相关性.综合考虑上述缺陷,利用互信息计算标记权重,由此设计特征和标记集间的相关度,初选与标记集相关度高的特征,提高特征与标记集之间的相关性.ReliefF是一种基于过滤式与特征加权的特征选择算法.陈平华等[6]结合ReliefF和多标记贡献值改进特征权值,基于互信息与ReliefF设计了多标记特征选择算法.但是这种方法未计算标记之间的相关性.REYES等[7]提出了扩展的多标记ReliefF的特征选择模型.但是,该模型未涉及特征间的相关性和冗余性.刘海洋等[8]利用ReliefF算法度量标记间的依赖关系,提出了基于ReliefF剪枝的多标记分类算法,但是,该算法未考虑特征与标记的相关性.针对以上算法存在的问题,本文改进ReliefF方法,引入标记权重构建特征权值更新公式,提高特征与标记间的相关性.
最大相关最小冗余算法是一种有效的过滤式特征选择模型,其评价函数考虑了特征与类别、特征与特征之间的相关性,因此基于mRMR的多标记特征选择得到了越来越多的关注.LI等[9]为了选择更相关和紧凑的特征子集以及探索标记相关性,基于互信息和mRMR构造了多标记特征选择模型.但是该算法计算复杂度较高.LIN等[10]考虑了标记之间的相关性、特征依赖性与冗余性,基于mRMR设计了多标记特征选择模型.但是,它未涉及特征和标记之间的相关性而造成分类精度低且时间代价大.HUANG等[11]将邻域逼近精度与mRMR结合,基于邻域粗糙集构建了多标记特征选择方法.但是该方法的计算复杂度较大.SUN等[12]提出了一种基于模糊邻域粗糙集和mRMR的缺失标记特征选择算法.然而,该算法没有考虑标记间相关性,造成去除冗余特征精度不高,不能完全剔除所有的冗余特征,降低多标记分类的预测结果.基于上述分析,使用互信息和标记权重改进最大相关算法,提出了新的mRMR评价准则,以此来衡量标记间的相关性以及特征之间的冗余度,有助于对多标记数据集去除冗余特征,获得最佳分类性能.
针对传统ReliefF算法仅能处理单标记数据并且未充分考虑特征和标记集之间的相关性,以及传统mRMR算法没有考虑标记间相关性而造成分类精度偏低等问题,对传统ReliefF算法和mRMR算法进行改进,提出了基于ReliefF和mRMR的多标记特征选择算法.首先,根据标记和标记集之间的互信息定义相关度,计算该相关度所占的比例来构建新的标记权重,构造特征和标记集之间的相关度,初选与标记集相关度较高的特征;然后,计算对象在特征上的距离,构建新的特征权值更新公式,并结合标记权重改进多标记ReliefF特征选择模型;最后,结合互信息和标记权重定义最大相关性,使用标记权重值与特征权值之和构建新的mRMR评价准则,有效提高模型的分类性能.
1 基础理论
1.1 互信息
给定A={a1,a2,…,an}为一个随机变量,p(ai)为变量ai的先验概率,则A的信息熵[13]表示为:
(1)
给定A={a1,a2,…,an}和B={b1,b2,…,bm}为随机变量,p(ai,bj)为A和B的联合概率,i=1,2,…,n,j=1,2,…,m,则A和B的联合信息熵[13]表示为:
(2)
给定A={a1,a2,…,an}和B={b1,b2,…,bm}为随机变量,p(bj|ai)为条件先验概率,i=1,2,…,n,j=1,2,…,m,则B在给定A下的条件熵[13]表示为:
(3)
随机变量A和B的互信息[13]表示为:
(4)
然后对互信息量进行归一化处理[13],归一化处理公式表示为:
(5)
易证明NMI(A;B)∈[0,1].NMI(A;B)=0表示A和B相互独立,NMI(A;B)=1表示可通过A和B之一确定另一个.
1.2 ReliefF算法
在ReliefF算法中,两个对象R1和R2在特征f上的距离[14]为:
(6)
其中,R1(f)表示对象R1在特征f上的值;R2(f)表示对象R2在特征f上的值;max(f)表示在特征f上的最大值,min(f)表示最小值.更新每个特征的权重的公式为:
(7)
其中,Hj和Mj分别代表对象R的第j个近邻同类对象和异类对象,diff(f,R,Hj)和diff(f,R,Mj)分别表示对象R与Hj和Mj分别在f上的距离,m为算法的迭代次数,k为近邻对象数,LRi是对象Ri的标记,P(LRi)是对象Ri所属标记的概率,P(l)表示标记l的概率.
2 多标记特征选择方法
2.1 标记权重
假设一个多标记决策系统表示为MDS=〈U,C,D,T〉[15],其中U={x1,x2,…,xn}是对象集;C是条件特征集和D是对象对应的标记空间;T={(xi,ti)|i=1,2,…,n}是在标记上的映射关系.若对象xi有第l个类别标记,记为ti(l)=1,否则记为ti(l)=0;且∑ti≥1,其中每个对象xi由f维表示,即xi∈Rf,对应的标记集由ti∈{0,1}l表示,这里l∈D.
为了解决未考虑特征和标记集之间的相关度而造成分类精度偏低的问题,利用互信息和标记权重,计算特征和标记集之间的相关度,使其有效筛选出与标记集相关度较高的特征子集.
定义1在MDS=〈U,C,D,T〉中,L⊆D,lk∈L,k=1,2,…,m,基于互信息计算标记和标记集之间相关度公式为:
(8)
定义2在MDS=〈U,C,D,T〉中,L⊆D,lk∈L,k=1,2,…,m,计算每个标记和标记集相关度,并计算其相关度的和,用两者的比例来定义标记权重为:
(9)
定义3在MDS=〈U,C,D,T〉中,F⊆C,fj∈F,j=1,2,…,z,L⊆D,lk∈L,k=1,2,…,m,根据互信息和标记权重计算特征f和标记集L之间的相关度为:
(10)
2.2 改进的ReliefF
为了解决传统ReliefF不适用于多标记特征选择的问题,根据标记权重设计新的ReliefF模型,由此构建特征权值更新公式,提高ReliefF算法的分类性能.
定义4在MDS=〈U,C,D,T〉中,X⊆U,xi,yi∈X,i=1,2,…,n,F⊆C,fj∈F,j=1,2,…,z,任意两个对象xi和yi在特征fj上的距离被定义为:
(11)
其中,xi(fj)是xi在fj上的特征值;yi(fj)是yi在fj上的特征值;max(fj)和min(fj)分别是fj在对象空间上的最大值和最小值.
定义5在MDS=〈U,C,D,T〉中,X⊆U,xi∈X,i=1,2,…,n,F⊆C,f∈F,L⊆D,lk∈L,k=1,2,…,m,结合标记权重和距离定义特征权重更新公式为:
(12)
其中,NMl(xi)是在l中xi的最近邻异类对象,NHl(xi)是在l中xi的最近邻同类对象.diff(xi,NMl(xi))和diff(xi,NHl(xi))分别是在f下xi在l中与其最近异类对象的距离和最近同类对象的距离.
2.3 改进的mRMR
为解决mRMR未涉及标记之间的相关性,导致删除冗余特征后的分类精度出现不理想的问题,运用互信息和标记权重更新最大相关性公式,并结合特征权值之和,提出新的mRMR评价准则,并将其应用于多标记特征选择.
定义6在MDS=〈U,C,D,T〉中,L⊆D,l∈L,F⊆C,fj∈F,j= 1,2,…,z,结合互信息和标记权重定义最大相关性的计算公式为:
(13)
定义7在MDS=〈U,C,D,T〉中,F⊆C,fi,fj∈F,i,j=1,2,…,z,基于互信息定义最小冗余性的计算公式为:
(14)
定义8在MDS=〈U,C,D,T〉中,特征集合F⊆C,L⊆D,l∈L,结合特征权重定义新的mRMR计算公式为:
(15)
其中,∑w(F)为特征集合F中每个特征的特征权重之和.
2.4 多标记特征选择算法
由此,设计基于ReliefF和mRMR的多标记特征选择算法(Multilabel feature selection algorithm using ReliefF and mRMR,MFSRM).首先计算新的标记权重和每个特征和标记集之间的相关度,初次筛选特征子集;然后计算特征权重选择出中间特征子集;最后计算MR值得到最终特征排序.其伪代码为:
算法1 MFSRM
输入MDS=〈U,C,D,T〉.
输出 最优特征子集R.
步骤1 For每个标记l∈D和每个特征f∈C;
步骤2 根据式(9)和式(10)分别计算标记权重WOL(lk)和特征和标记集之间的相关度Corr(f,D);
步骤3 End For;
步骤4 根据特征和标记集之间的Corr(f,D)值初次筛选出特征子集R0(特征个数关系:|R0|=2|R1|=4|R|).
步骤5 Forxi∈U;
步骤6 计算xi的NMl(xi)和NMl(xi);
步骤7 End For;
步骤8 For 每个特征f∈C;
步骤9 根据式(12)计算特征权重wf;
步骤10 End For;
步骤11 根据特征权重选择出中间特征子集R1(特征个数关系:|R1|=2|R|).
步骤12 For 特征子集R1;
步骤13 根据式(15)计算MR(R1);
步骤14 End For ;
步骤15 对MR值进行排序并选择前c个特征作为最终特征子集R.
3 实验分析
3.1 实验准备
为了测试MFSRM算法的分类性能,选取了Mulan数据库(http://mulan.sourceforge.net)中的8个数据集进行实验,表1描述了8个数据集的详细信息.依据文献[16]的平均分类精度(Average Precision,AP)、覆盖率(Coverage,CV)、汉明损失(Hamming Loss,HL)、1错误率(One Error,OE)、排序损失(Ranking Loss,RL)指标作为分类性能和排序性能的5个评价指标.为了充分验证本文算法的有效性,采用上述的5个基于对象的评价指标和选择特征比例来评价算法的性能,其中AP值越大表示算法性能越好(最优值为1),其余4个指标值和特征选择比例越小则算法性能越好.采用多标记K最近邻(Multilabel k-nearest neighbor,ML-KNN)分类器,设置近邻个数为10,平滑参数为1.实验环境为Windows 10、CPU Intel(R)Core(TM)i5-8500 3.00 GHz和内存8.00 GB,采用MATLAB 2019a工具箱进行编码.
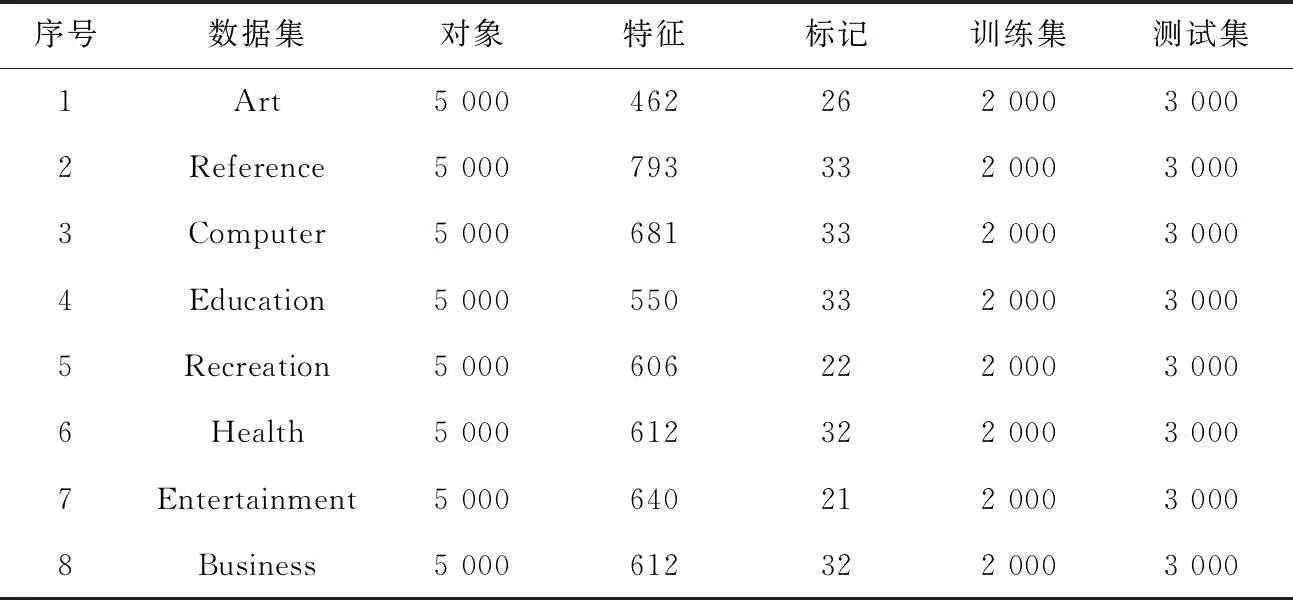
表1 8个多标记数据集的信息
3.2 ML-KNN分类器上的实验分析
为了充分展示MFSRM算法在不同数据集上的有效性,选择5种对比算法:MLNB(Feature selection for multi-label naive Bayes classification)[17]、PMU(Pairwise Multivariate Mutual Information)[18]、MLRF(Relief for multi-label feature selection)[19]、MFSR(Multi-label feature selection algorithm based on improved ReliefF)[20]和WFSNR(Weak label feature selection method based on neighborhood rough sets and Relief)[21],进一步呈现MFSRM算法在ML-KNN分类器上的5个指标(AP、HL、CV、OE和RL)的实验结果.各个数据集进行实验时所选的特征个数见文献[22].表2描述了MFSRM算法与5种多标记特征选择算法在5个指标下的实验结果.

表2 8个数据集上6种算法在5个指标下的比较结果
由表2可知,在AP指标下,MFSRM算法在除Education外的7个数据集上,MFSRM算法的实验结果均优于其他5种算法;尤其在Recreation数据集上,MFSRM算法比次优的MLNB算法高0.066;在Education数据集上,MFSRM算法为次优,比最优的MFSR算法低0.116 2,但MFSRM算法比其他4种算法高0.013 2~0.072 3.在HL指标下,MFSRM算法在8个数据集上的表现均为最优.在CV指标下,在Business数据集上,MFSRM算法比最优的PMU算法和次优的MFSR算法分别高0.057 4和0.008 2;在Health数据集上,MFSRM算法比最优的PMU算法高0.072;但在其他6个数据集上,MFSRM算法均优于其他5种多标记特征选择算法.在OE指标下,在这8个数据集上,MFSRM算法均为最优.在RL指标下,MFSRM算法在除Business和Health以外的6个数据集上的实验结果均为最优;在Business数据集上,MFSRM算法比最优的PMU算法高0.001 6;在Health数据集上,MFSRM算法为次优,比最优的PMU算法高0.001 9,但总体上仍优于其他4种算法;在Recreation数据集上,MFSRM算法明显优于其他5种算法,比其他算法低0.014 9~0.034 6.从整体来看,MFSRM算法在大部分数据集上的表现均为最优,在极个别数据集上的指标表现为次优,如在CV和RL指标下,Business和Health这2个数据集上MFSRM算法的表现较差,原因是Business和Health这2个数据集是稀疏矩阵数据集,证明了MFSRM算法在这类稀疏矩阵数据集上的分类性能不佳.通过观察发现:这6种算法在Art和Recreation这2个数据集上的AP值均过低(低于或略高于50%).究其原因可能是:在Art和Recreation这2个数据集上,收集数据和划分数据时可能对平均分类精度有所限制,从而导致在现存大多数流行算法的实验结果中呈现的平均分类精度均不高.综上所述,MFSRM算法的性能得到了有效地提升.
在本节实验的第2部分是将MFSLM算法与第1部分的4种多标记特征选择算法:MLRF算法、PMU算法、MFSR算法和WFSNR算法作对比分析,给出表1中Art、Business、Computer、Entertainment、Reference这5个数据集各特征选择算法在不同特征比例下的分类情况.图1展示了5种算法在不同特征比例下AP指标的变化趋势对比图.由于篇幅限制,其余4个指标的变化趋势图可以单独提供.
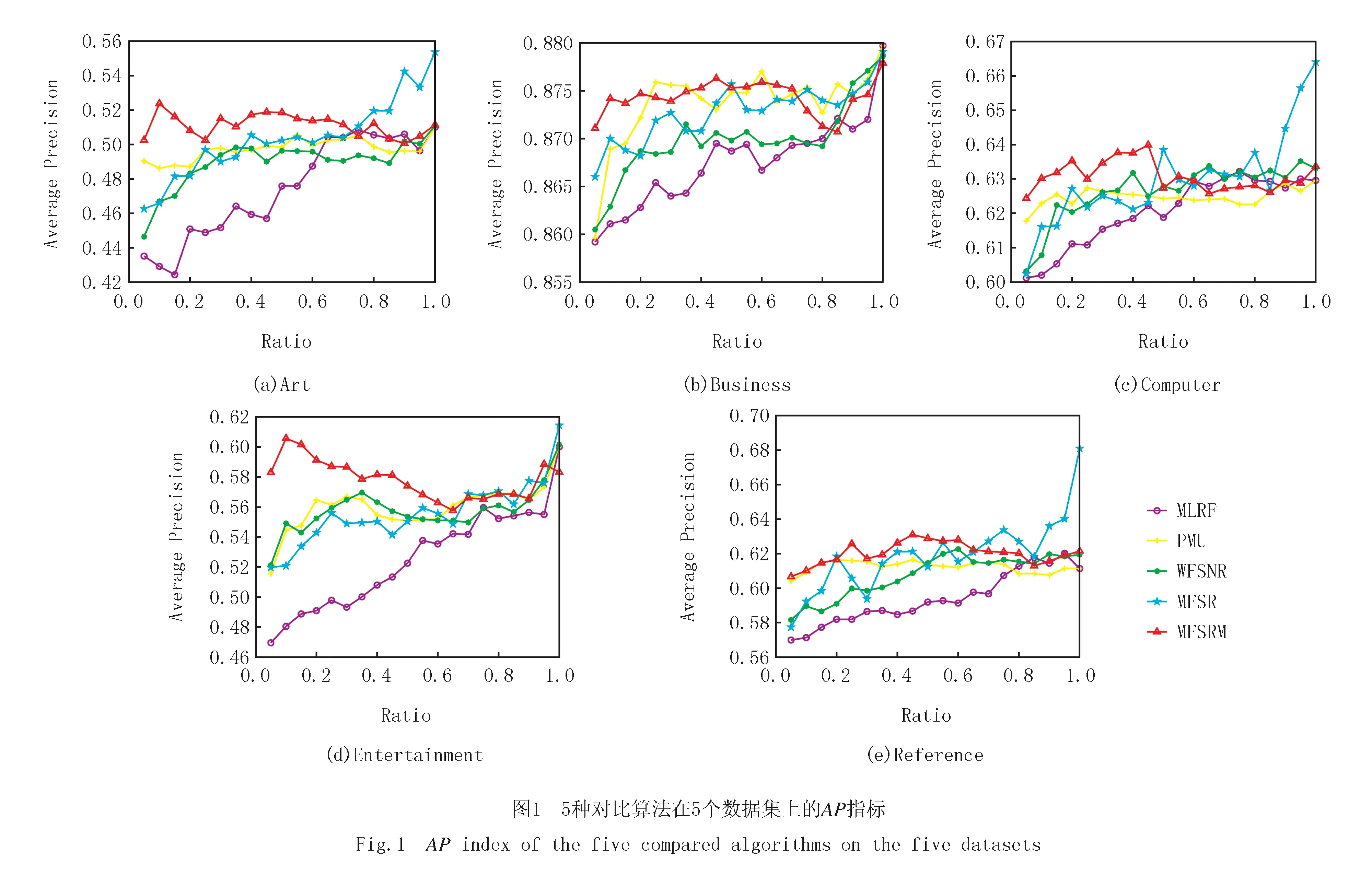
由图1可知,在AP指标下,在Art和Entertainment这2个数据集上,MFSRM算法在选择特征比例较小时,算法性能较好,在选择特征比例大于0.7时,MFSRM算法的性能差于MFSR算法.在Business数据集上,在选择特征比例为0.25~0.35时,MFSRM算法差于PMU算法;在选择特征比例为0.40~0.45和0.65~0.70时,MFSRM算法为最优;在选择特征比例大于0.5时,MFSRM算法性能较差.在Computer数据集上,在选择特征比例小于0.5时,MFSRM算法优于其他算法.在Reference数据集,MFSRM算法在选择特征比例较小时优于其他算法,但选择特征比例大于0.6时,MFSRM算法差于MFSR算法.
整体来看,在选择特征比例较小时,MFSRM算法优于其他4种算法,其原因可能是:在选择特征比例较大时,冗余特征较多,分类性能下降.但综上所述,MFSRM算法的改进是有效的,提升了算法的性能.
3.3 统计分析
本节使用Friedman测试[23]和Nemenyi测试[24]验证多标记特征选择算法对于不同数据集分类结果的统计重要性.Friedman测试公式为:
(16)
(17)
其中,T是数据集的数量,s代表对比算法数量,Ri是每个算法在所有数据集上的平均排序.临界距离表示为:
(18)
其中,qα是测试临界值,α是Nemenyi测试中的一个重要指标.
参考文献[23]的统计计算方法,检测本文MFSRM算法与其他5种对比算法在AP、HL、CV、OE和RL这5个指标上是否存在显著差异.表2中的实验结果对应的统计结果如表3所示,CD图如图2所示.图2展示了表2中5个指标上的6种算法的对比结果.接下来,使用了Friedman检验判断这6种算法在分类性能上是否相同.由文献[25]中表2.6的F检验的常用临界值可知,在α=0.1,s=6且T=8时,F检验临界值是2.019,而由表3可知,这5个评价指标的FF值均大于临界值2.019.因此拒绝“所有算法性能相同”这个假设,需要进行后续检验.于是,本文采用Nemenyi测试执行后续检验.而对于Nemenyi测试,当q0.1=2.589,s=6且T=8时,CD值为2.421 8.文献[25]指出:若两个算法存在性能显著不同,则它们的平均序值之差会超出临界值CD,否则它们之间有一条直线连接,表示它们没有显著差别.从图2中可以得到如下结论:本文MFSRM算法在5个评价指标上分类性能均排名第1.详细来讲:在AP指标上,MFSRM算法与WFSNR和MLRF这2种算法的性能显著不同,与其他3种算法的分类性能没有显著差别;在HL、CV和RL这3种指标上,MFSRM算法与PMU和MLNB这2种算法之间不存在显著性差异,MFSRM算法与MFSR、WFSNR和MLRF这3种算法之间存在显著性差异;在OE指标上,MFSRM算法与PMU和MFSR这2种算法之间不存在显著性差异,MFSRM算法显著优于与MLNB、WFSNR和MLRF这3种算法.总之,与其他5种对比算法相比,MFSRM算法表现出了良好的分类性能.

表3 5个评价指标下6种算法的统计结果
4 结 论
针对一些多标记特征选择算法未充分考虑特征和标记集之间的相关性导致算法分类性能偏低的问题,本文考虑标记之间的相关性以及特征与标记集之间的相关性,提出了基于ReliefF和mRMR的多标记特征选择算法.首先,基于互信息计算标记和标记集间的相关度来改进标记权重,并结合标记权重计算特征和标记集之间的相关度,提高了特征和标记集之间的相关性.然后,改进ReliefF模型,结合标记权重和基于对象在特征上的距离更新特征权值公式,提高算法分类精度.最后,结合互信息和标记权重定义最大相关性,使用特征权值之和构建了新的mRMR评价准则,得到最优特征子集.在8个多标记数据集上进行实验,结果表明所提算法性能有所提高.

