基于神经网络的微波滤波器设计综述
2023-10-31张安学杜浩戴新月杨倩郭诚廖学文
张安学,杜浩,戴新月,杨倩,郭诚,廖学文
(西安交通大学 电子与信息学部,西安 710049)
在微波领域的迅速发展中,目前已经出现很多新型的滤波器结构[1-2],主要研究方向是通过寻找新的结构或材料,实现可重构或可支撑性和小型化.随着微波滤波器领域研究的不断深入,也越来越需要寻找新的建模技术[3-4].通用的数值方法使用商业软件创建微波器件的3维模型,但计算过程十分耗时,当微波器件结构复杂时,计算可能需要数小时甚至数天[5-6].
基于以上所述的缺点,在微波器件领域中除了传统方法之外,基于神经网络的方法也被广泛应用.深度学习作为人工智能技术的分支,已经成功地应用在众多领域,如图像处理[7]、声音处理[8]和金融市场预测[9].神经网络是深度学习的基础,它是受到人类大脑结构启发而诞生的一种算法,具有可以精确地模拟任意非线性函数的能力.经过学习的神经网络可以轻松地模拟复杂的非线性关系.凭借这种优势,基于神经网络的研究方法已经广泛地应用于微波领域[10-15].与传统的微波器件设计方法相比,基于神经网络的设计方法可以大大加快分析或合成微波器件的过程[16-17],在更短时间内设计出满足设计要求的器件模型.
本文在介绍了神经网络基础的模型结构和常用的训练方法之后,对现有的基于神经网络的微波器件设计方法进行了对比和综述.在此基础上,提出一种基于训练和精调的神经网络方法,在双通带滤波器LC电路的参数提取实验中验证其有效性.提出一种基于数据自生成的神经网络方法,在带通滤波器的结构参数估计和带宽可重构带通滤波器的设计实验中进行了实例验证.实验结果表明,神经网络可以有效利用滤波器的S参数信息,经过学习训练之后,准确的预测出满足设计要求的LC电路参数/器件结构参数,减少滤波器设计过程的人工干预,实现更加快速高效的器件设计过程.
1 神经网络概述
1.1 神经网络的结构
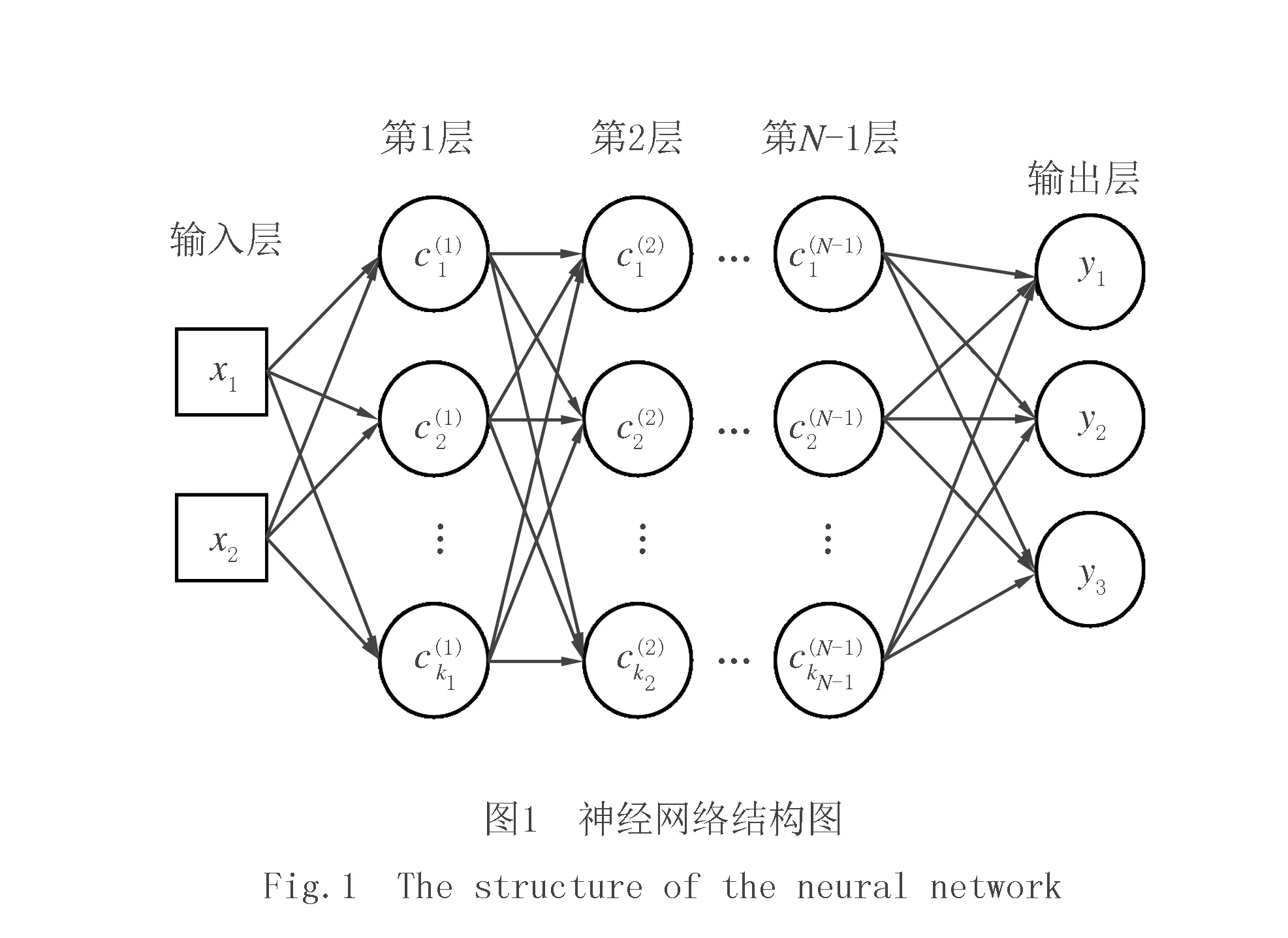
神经网络的基本结构包括输入层、隐含层和输出层.输入层是神经网络的第一层,用于输入特征矩阵,每个神经元上都是一个特征向量;隐含层至少一层,前后连接输入层和输出层,隐含层中任意2层的神经元都是互相连接的,每个神经元上都有一个激活函数,第N+1层的神经元处理的是第N层神经元经过激活函数之后的数据;输出层是神经网络的最后一层,用于输出神经网络的预测结果.在实际应用中,隐含层的层数以及每层的神经元个数如何设定会影响最终的训练精度和算法最终的学习效果,需要根据设计要求来确定.
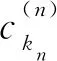
1.2 神经网络的训练
基于神经网络的优化算法中最重要的步骤就是对网络的训练,训练的主要目的是最小化训练误差.训练过程中不断更新网络权重,降到要求的误差之内后得到最终输出结果.
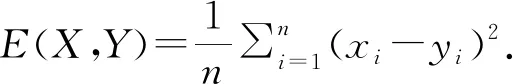
更新网络权重通常使用反向传播算法[18]、拟牛顿法[19]和共轭梯度法等.这些方法可以有效降低训练误差.针对容易陷入局部最小的复杂优化问题,可以使用全局优化算法来解决,如遗传算法[20]、模拟退火算法[21]等.
神经网络的训练方式包括在线训练和离线训练2种.在线训练又称逐样本训练,当神经网络输入一个训练样本时更新权重;离线训练又称批量训练模式,给神经网络输入全部训练样本之后再对权重进行一次更新.
2 基于神经网络的微波器件设计方法
2.1 传统神经网络建模方法
结构参数的优化是微波设计中不可回避的重要任务,但随着滤波器参数个数的增加,优化时间也随之增加.因此,基于神经网络的微波器件设计方法受到广泛关注和研究.早在1993年,就有文献中提出将神经网络应用于微带电路的设计中[22].之后,有大量文献中提出神经网络在模拟电磁仿真的学习之后,根据滤波器的结构参数计算频率特性,可以作为耗时的电磁仿真软件的替代模型,加快滤波器优化过程[23-29].针对复杂的微波器件,神经网络的输入输出关系也会更加复杂、在不增加网络结构复杂度的情况下,建立神经网络正向模型,更新正向模型的输入参数,使模型输出与理想输出的误差达到最小[30].
2.2 基于极限学习机的设计方法
极限学习机是一种单隐层神经网络,它适用于无微分激活函数,并在很大程度上避免了训练会遇到的某些问题,如停止准则、学习率、训练时间和局部最小[31].极限学习机通过固定输入层和隐含层的网络权重,将学习过程转化为矩阵计算,相比传统神经网络中的反向传播算法其学习速度更快[32].由于这种方法的计算效率较高,目前已经较好地应用于微波器件的设计[33-34].内核极限学习机是极限学习机的扩展版本[35],与极限学习机相比引入了内核函数,且隐含层的节点个数是没有限制的,通过引入的核函数可以获得较好的泛化性能,并且降低计算成本.动态调整内核极限学习机[36]中包含增加学习、简化学习和混合学习,当训练数据的样本数过少导致神经网络无法获得准确结果时,使用增加学习来解决欠拟合问题,当样本数过多而无法获得准确的结果时,使用简化学习来解决过拟合问题,当训练数据需要替换和扩展,则使用增加学习和简化学习相结合的混合学习,直接获得最终结果.
2.3 基于知识神经网络的设计方法
基于知识的神经网络[37]是一种将经验信息融入神经网络内部结构,将先验知识与神经网络的学习能力相结合的建模方法.在微波器件设计应用中,先验微波知识被嵌入到神经网络内部,微波知识通过提供额外的信息,如解析表达式[38],经验模型[39],或等效电路[40],补充了神经网络的学习和泛化能力.相比现有神经网络模型学习输入-输出关系的复杂性,基于知识神经网络的差分法和先验知识输入法具有更高的准确度[41].先验知识输入法神经网络将等效电路的S参数作为先验知识与神经网络相结合进行训练,可以获得更高的训练精度[42].当训练数据的样本数量有限时,在神经网络中增加经验知识可以补充其学习能力和泛化能力,减少收集大量训练数据的时间成本,加快建模速度[37,43].针对先验知识获取困难的问题,采用将神经网络与仿真软件相结合的方法,将ADS和电磁仿真软件HFSS的仿真结果作为神经网络的先验知识和指导信息,可以有效降低神经网络结构的复杂度[44].
2.4 神经网络和传递函数结合的设计方法
神经网络和传递函数的结合是电磁响应参数化建模的一种先进方法.在没有精确的等效电路或经验模型的情况下,用传递函数表示微波器件电磁响应随频率的变化.这种神经网络和传递函数相结合的方式也可以很好地用于电磁响应的参数化建模[45].
这种建模方法利用向量拟合技术获得电磁响应对应的传递函数系数作为神经网络的训练数据[46].神经网络的输入是器件结构的几何变量,输出是微波器件电磁仿真的S参数,经过训练,神经网络可以学习到传递函数系数与几何参数之间的非线性未知关系[47].
3 基于神经网络的带通滤波器设计
3.1 基于训练和精调的LC电路参数提取方法
上述大多基于神经网络的微波器件设计方法只对网络进行了训练过程,但是往往不能在短时间内达到较高的精度.基于深度信念网络[48-49]的思想,对神经网络采用先预训练后微调的学习算法,提出一种基于神经网络的双通带带通滤波器(DB-BPF,dual-band bandpass filter)的LC电路参数提取方法[50-51].
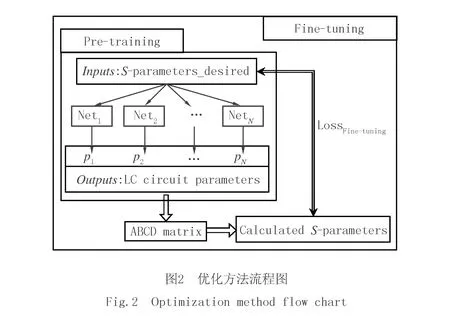
如图2所示,该参数提取方法由2个阶段组成.第一个阶段是用数据集对网络进行预训练,经过预训练的神经网络可以获得接近最优值的LC电路参数的初始值;第2个阶段是根据期望的频率响应对网络进行微调,微调的过程是对预先训练好的网络进行优化,以提高提取参数的精度,从而获得LC电路参数的最优值.训练数据除了S参数的幅度信息,还加上了相位信息,以提高网络提取参数的能力.
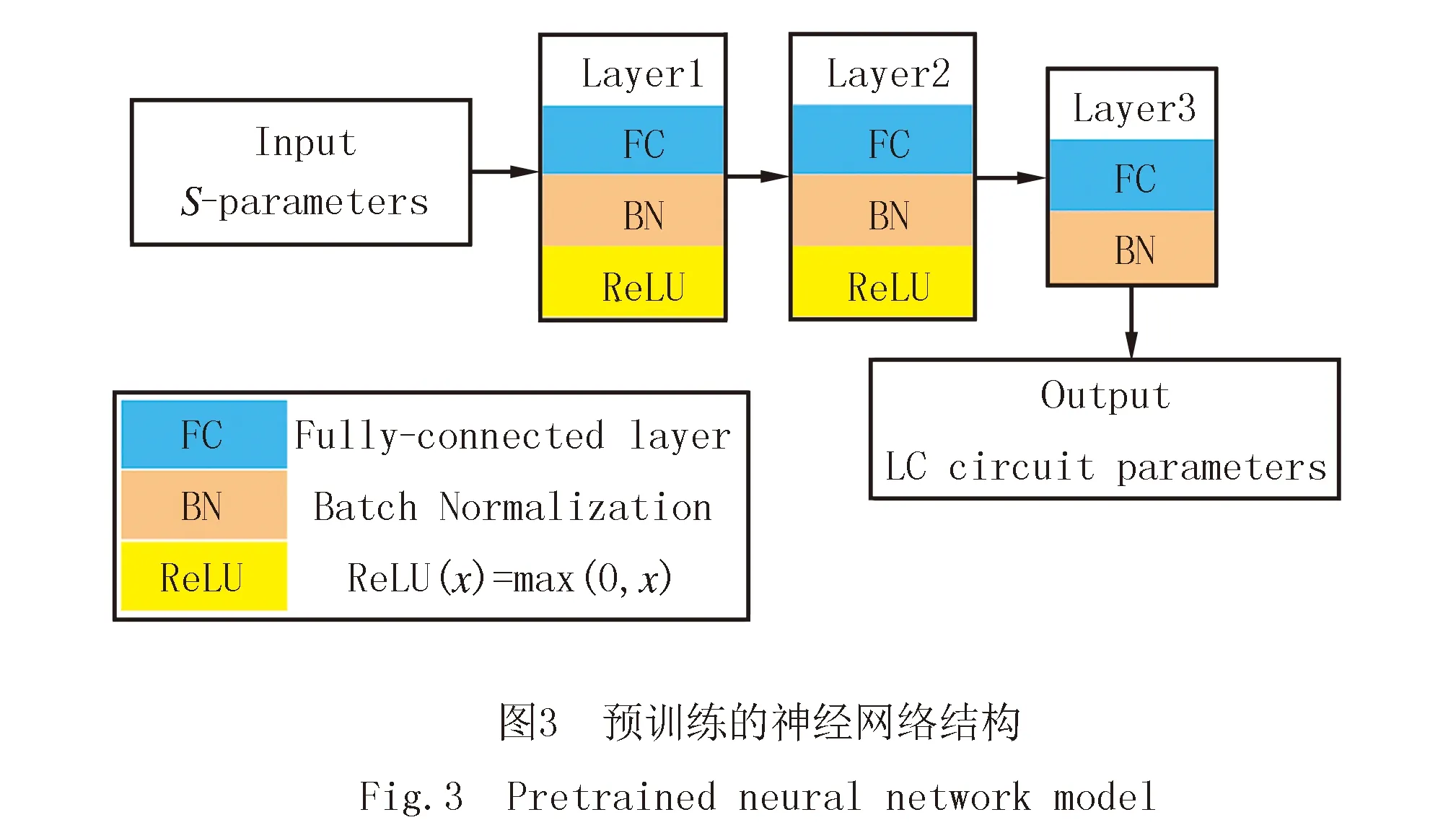
预训练的神经网络结构如图3所示,由于LC电路参数与滤波器频率响应之间是一种复杂的非线性关系,因此选择非线性表达能力较好的全连接层网络结构.前2层由全连接层、块归一化[52]和ReLU激活函数组成,第3层是输出层,没有激活函数.块归一化是一种归一化网络层,可以加快训练速度,提高网络的泛化能力.ReLU激活函数可以使网络收敛更快.
神经网络预训练的数据集包括输入数据和标签.标签是LC电路中的电感值和电容值,定义为P=p1,p2,…,pN,其中N表示LC电路参数的总个数.输入数据是根据A,B,C,D矩阵计算得到的频率响应.根据不同的电感和电容值,获得不同的S参数,收集10万组数据作为预训练的数据集.
如图2参数提取的第一阶段用N个网络分别预测N个LC电路参数,其中每个网络的结构如图3所示.使用Adam优化算法[53]更新各个网络的权值.训练过程中的损失函数为LTrain=MSE(Poutput,Plabel).N个神经网络经过预训练后,以目标S参数为输入,分别输出N个准确度不高的LC电路参数值.
使用第一阶段预训练的N个神经网络作为第2阶段的初始网络.参数提取的第2阶段是对神经网络进行微调,如图2所示,每个网络以目标S参数为输入,输出N个LC电路参数的预测值.然后通过求解LC电路的A,B,C,D矩阵方程,根据LC电路参数的预测值计算对应的S参数.每个网络的权值由损失函数LFine-tuning来更新,LFine-tuning=MSE(Scalculated,Sdesired).重复上述迭代步骤,直到计算S参数与目标S参数基本一致.迭代停止准则是LFine-tuning<0.000 1.经过微调后,N个网络可以分别输出N个最优LC电路参数值,最优LC电路参数值对应的频率响应与目标频率响应基本相同,满足设计要求.
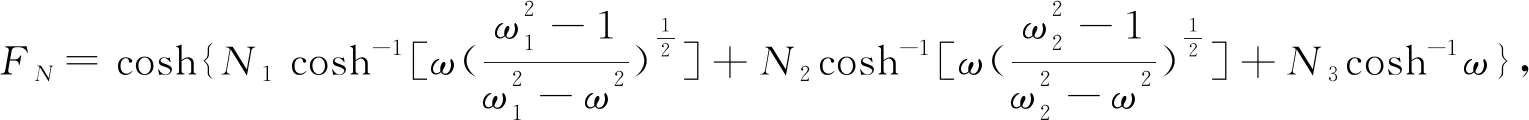
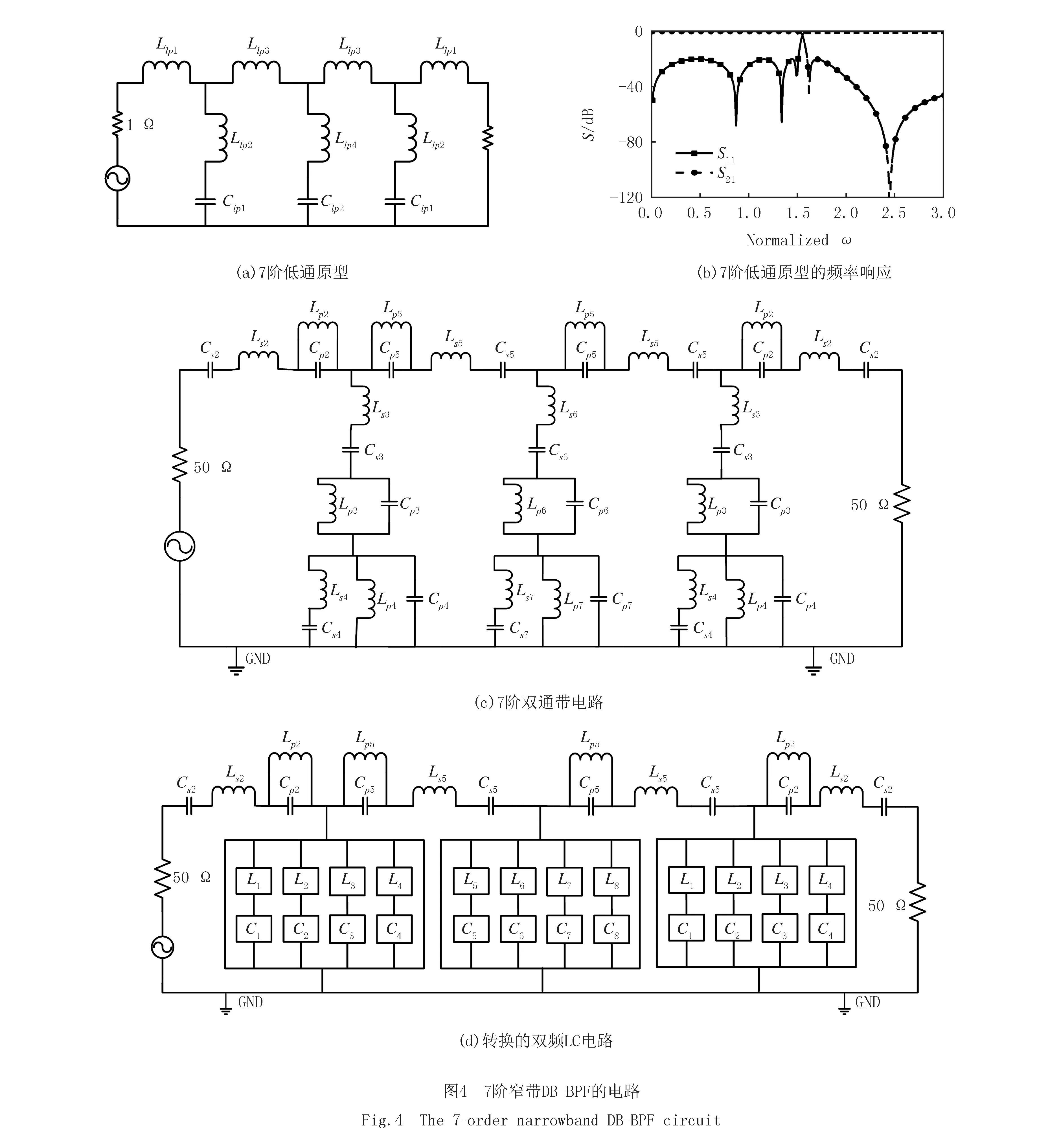
设计指标:Norder=7.0,N1=2.0,N2=4.0,N3=1.7阶低通原型及其响应如图4(a)和图4(b)所示.已知电路参数Llp1=0.770 nH,Llp2=0.380 nH,Llp3=1.073 nH,Llp4=2.160 nH,Clp1=1.110 pF,Clp2=0.446 pF.根据低通到双通带的频率转换方法得到如图4(c)所示的7阶双通带电路.电路参数可以根据设计要求计算得出.该电路给出了在微调阶段作为网络输入目标S参数(包括S11、S21的幅值和S11的相位).将图4(c)中的并联模块转化为4个并联串联谐振模块[54],得到如图4(d)所示的转换双频LC电路.对于该电路来说,需要提取的LC电路参数个数N=16,其中包括8个电容值和8个电感值,定义为C1,C2,…,C8,L1,L2,…,L8.根据这些参数使用A,B,C,D矩阵计算S参数,作为神经网络预训练的标签.神经网络预训练的数据集是在L和C的取值范围内均匀采样得到的,其中电容值范围是0.01~30.00 pF,电感值范围0.1 ~500.0 nH.
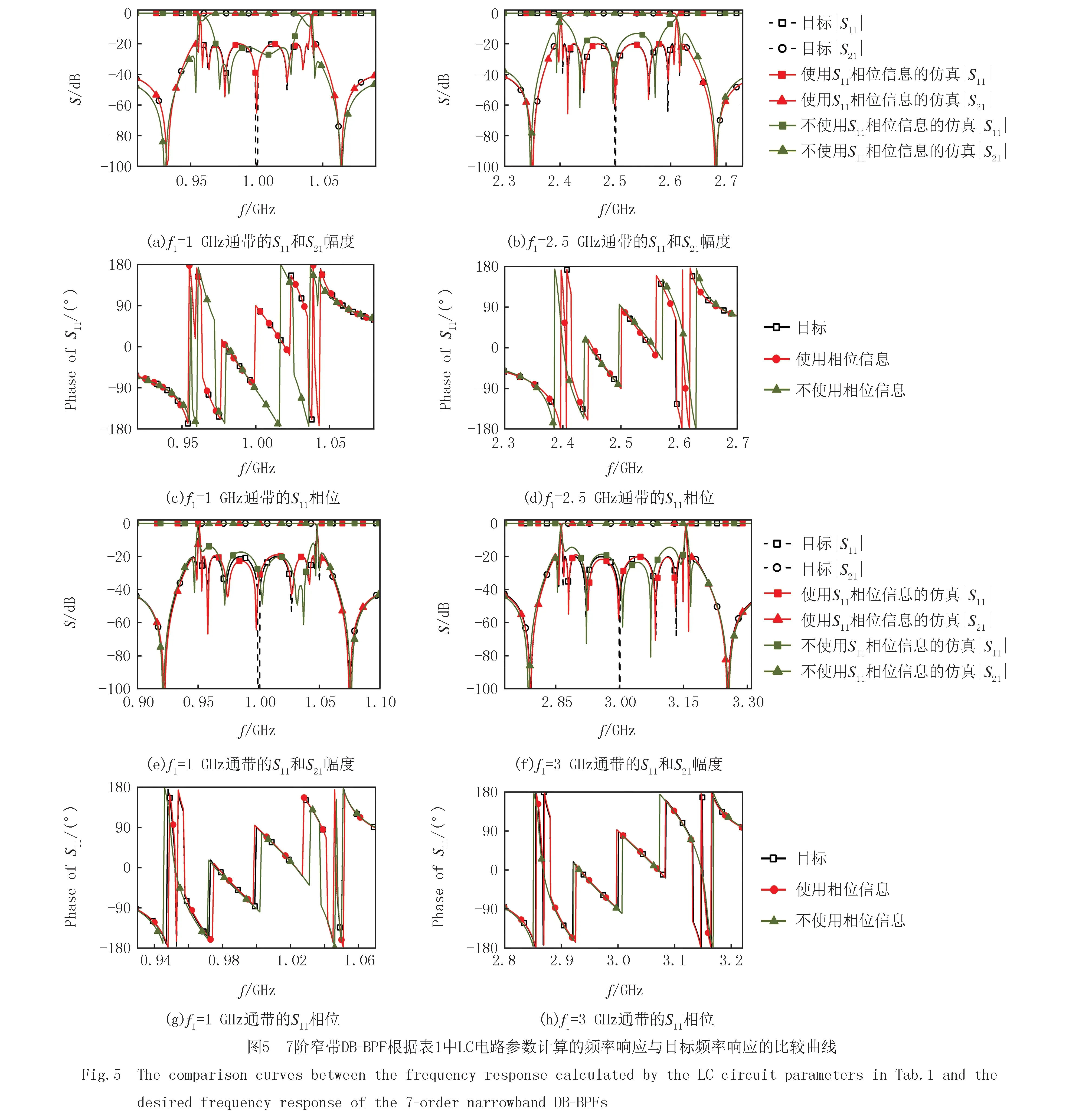
第1个7阶窄带DB-BPF,2个通带的中心频率分别为1.0 GHz和 2.5 GHz,2个通带的分数带宽分别为8.60%和8.56%.带内回波损耗20 dB,4个传输零点分别位于0.928 GHz、1.060 GHz、2.348 GHz和2.679 GHz.图4(c)所示的电路参数计算得:Ls2=20.424 9 nH,Cs2=0.496 1 pF,Lp2=18.382 4 nH,Cp2=0.551 2 pF,Ls5=28.462 2 nH,Cs5=0.356 0 pF,Lp5=25.616 0 nH,Cp5=0.395 5 pF,在0~3 GHz频带范围内以0.001 GHz的间隔计算S参数;第2个7阶窄带DB-BPF,2个通带的中心频率分别为1 GHz和3 GHz,2个通带的分数带宽分别为10.04%和10.07%.带内回波损耗20 dB,4个传输零点分别位于0.915 GHz,1.073 GHz,2.790 GHz和3.247 GHz.电路参数:Ls2=15.318 7 nH,Cs2=0.551 2 pF,Lp2=20.424 9 nH,Cp2=0.413 4 pF,Ls5=21.346 6 nH,Cs5=0.395 5 pF,Lp5=28.462 2 nH,Cp5=0.296 6 pF,在0~3.5 GHz频带范围内以0.001 GHz的间隔计算S参数.
对于这2个7阶DB-BPFs,通过上述的LC电路参数提取方法,经过>10 min的训练和<10 min的微调,提取出LC电路参数的最优值如表1所示,对是否使用相位信息的结果也进行对比.根据表1的LC参数计算得到的频率响应如图5所示.
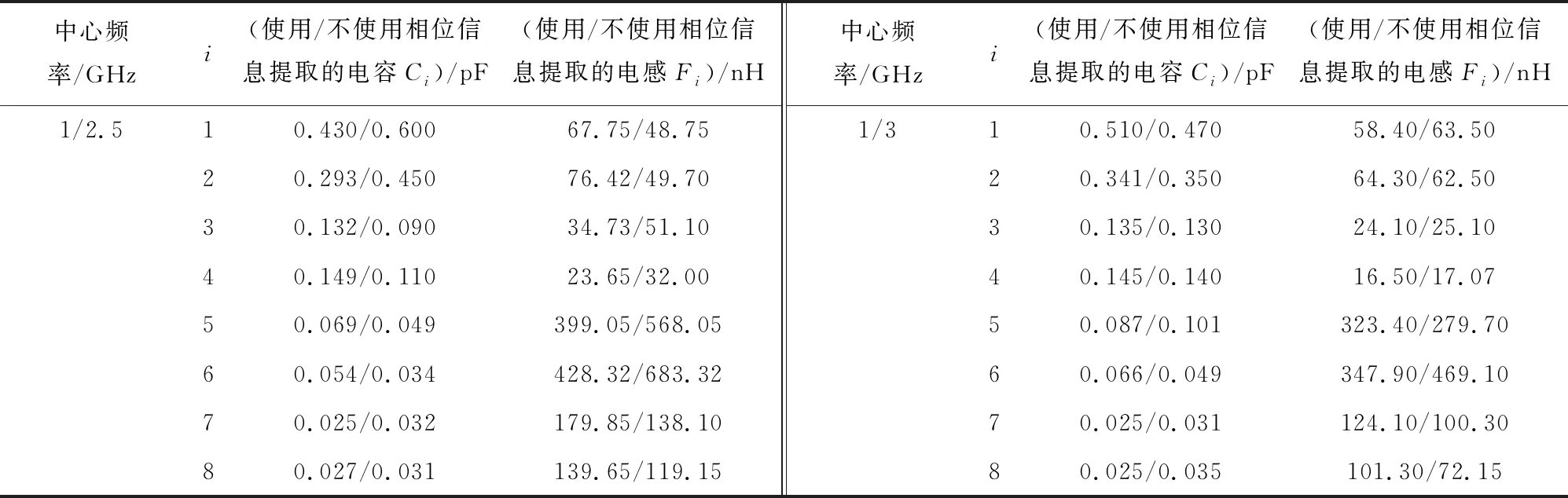
表1 不同中心频率的7阶窄带DB-BPFs的LC电路参数
实验结果表明,基于训练和精调的神经网络可以利用相位信息在短时间内获得不同中心频率、不同带宽的DB-BPF的最优LC电路参数.由最优LC电路参数计算得到的频率响应与期望频率响应几乎一致.这种方法还可以扩展应用到其他类型的滤波器的电路.
3.2 基于数据自生成的结构参数估计方法
对于前面综述的大多数方法,在滤波器设计中使用的基于训练的神经网络的方法,收集数据集都是一个烦琐的过程,需要耗费大量的时间和精力,尤其是在参数数量较大的情况下成本倍增.
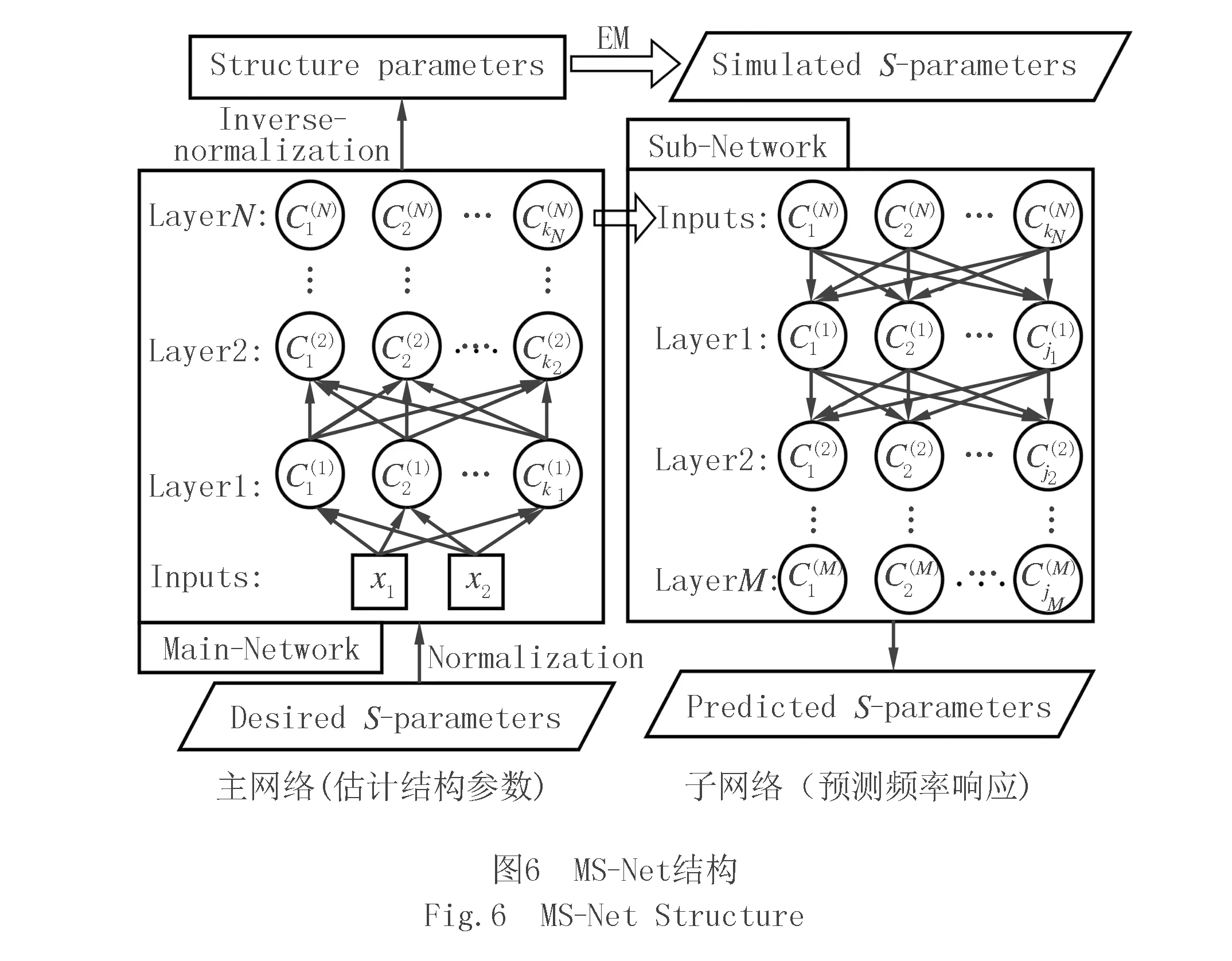
针对上述难题,提出一种基于数据自生成的微带带通滤波器(BPF)的结构参数估计方法[55].设计一种神经网络MS-Net,如图6所示,包括主网络Main-Net和子网络Sub-Net,分别用于估计BPF的结构参数和频率响应.与其他基于神经网络的优化方法相比,MS-Net可以在学习过程中生成自己的数据,而不需要收集数据集和对网络进行预训练.MS-Net在每一次学习时,主网络输出的估计结构参数可以作为子网络的学习数据.在迭代学习过程中,主网估计的结构参数将逐渐满足设计要求.
基于神经网络的微带带通滤波器的设计过程为:
1)目标S参数是神经网络的学习目标,根据需要设计的滤波器的理想耦合矩阵或理想滤波特性函数计算获得;
2)主网络以目标S参数作为输入,输出滤波器的估计结构参数,并将其送入电磁仿真得到仿真的S参数.之后,子网络将主网络的输出和相应的仿真S参数作为自己的学习数据和标签,对电磁仿真过程进行建模.MS-Net的整个学习过程也是数据自生成的过程,不需要在开始学习之前进行额外的数据收集过程;
3)当仿真S参数,即对主网络输出的预测结构参数进行电磁仿真得到的频率响应,满足滤波器的设计要求时,学习停止;
4)学习完成之后,根据主网络输出的预测滤波器结构参数,对滤波器结构进行建模,设计完成.
在学习过程中,主网络的损失函数LM-Net是目标S参数和预测S参数的均方误差,子网络的损失函数LS-Net是仿真S参数和预测S参数的MSE.LM-Net=MSE(Spredicted,Sdesired),LS-Net=MSE(Spredicted,Ssimulated).MS-Net利用Adam算法[53]根据计算的误差更新权值.当子网络的训练误差逐渐降低,其模拟电磁仿真过程的能力越强;当通过主网络估计的结构参数进行电磁仿真得到的仿真S参数越来越逼近于目标S参数时,主网估计的结构参数将逐渐满足设计规范.
基于上述结构参数估计方法分别设计1个3阶窄带BPF和1个5阶宽带BPF.主网络的输入xmain=(S11,desired,S21,desired),输出是ymain=(y1,y2,…,yL),其中L表示待估计的结构参数个数.子网络的输入是主网络的输出xsub=ymain,输出是ysub=(S11,predicted,S21,predicted).

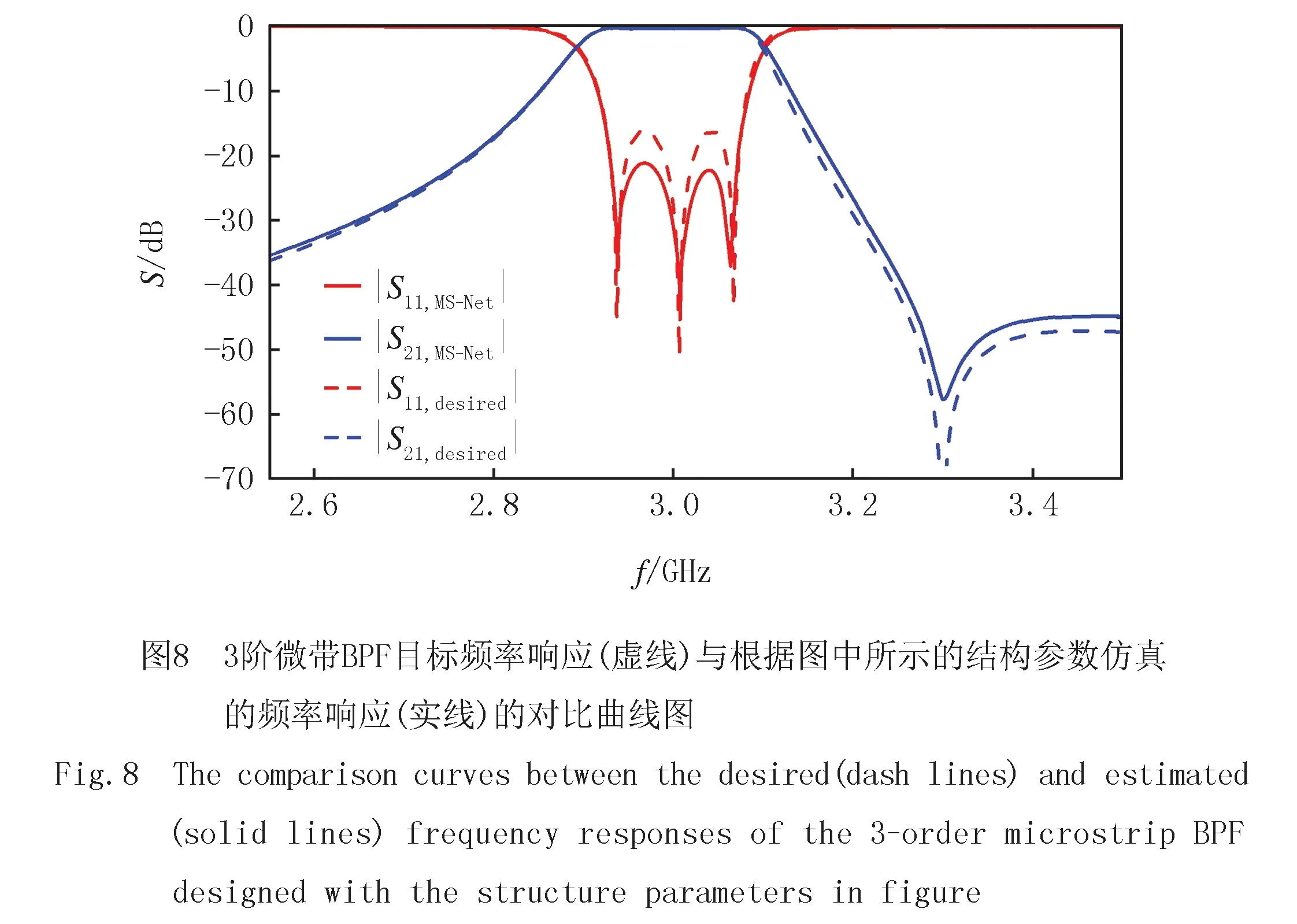
第一个例子是并联耦合结构的微带BPF,如图7所示.需要估计的结构参数的数量L=4,各参数的取值范围如表2所示.滤波器的设计要求[56]是中心频率3 GHz,分数带宽FBW为 5%,带内回波损耗RL为16 dB,传输零点3.3 GHz.使用2个5层神经网络作为MS-Net的主网络和子网络,每层的神经元个数如表3所示.目标S参数根据理想耦合矩阵计算得到.学习过程在1 h内,得到一组满足设计要求的结构参数(表1).其电磁仿真频率响应如图8所示,带内回波损耗可以优于-20 dB,虚线表示目标频率响应.与文献[14]相比,该方法无需收集数据集来训练神经网络,在节省大量时间成本的同时很快实现了滤波器模型的设计.

表2 3阶带通滤波器的结构参数范围

表3 用于3阶带通滤波器的MS-Net中每层神经元数

表4 5阶带通滤波器的结构参数范围
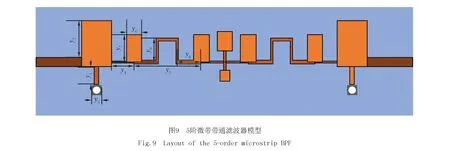
第2个例子是宽带BPF,如图9所示,需要估计的结构参数的数量L=9,各参数的取值范围如表5所示.设计的滤波器中心频率2 GHz,分数带宽40%,带内损耗15 dB,2个传输零点分别位于1.53 GHz和2.55 GHz.

表5 用于5阶带通滤波器的MS-Net中每层神经元数
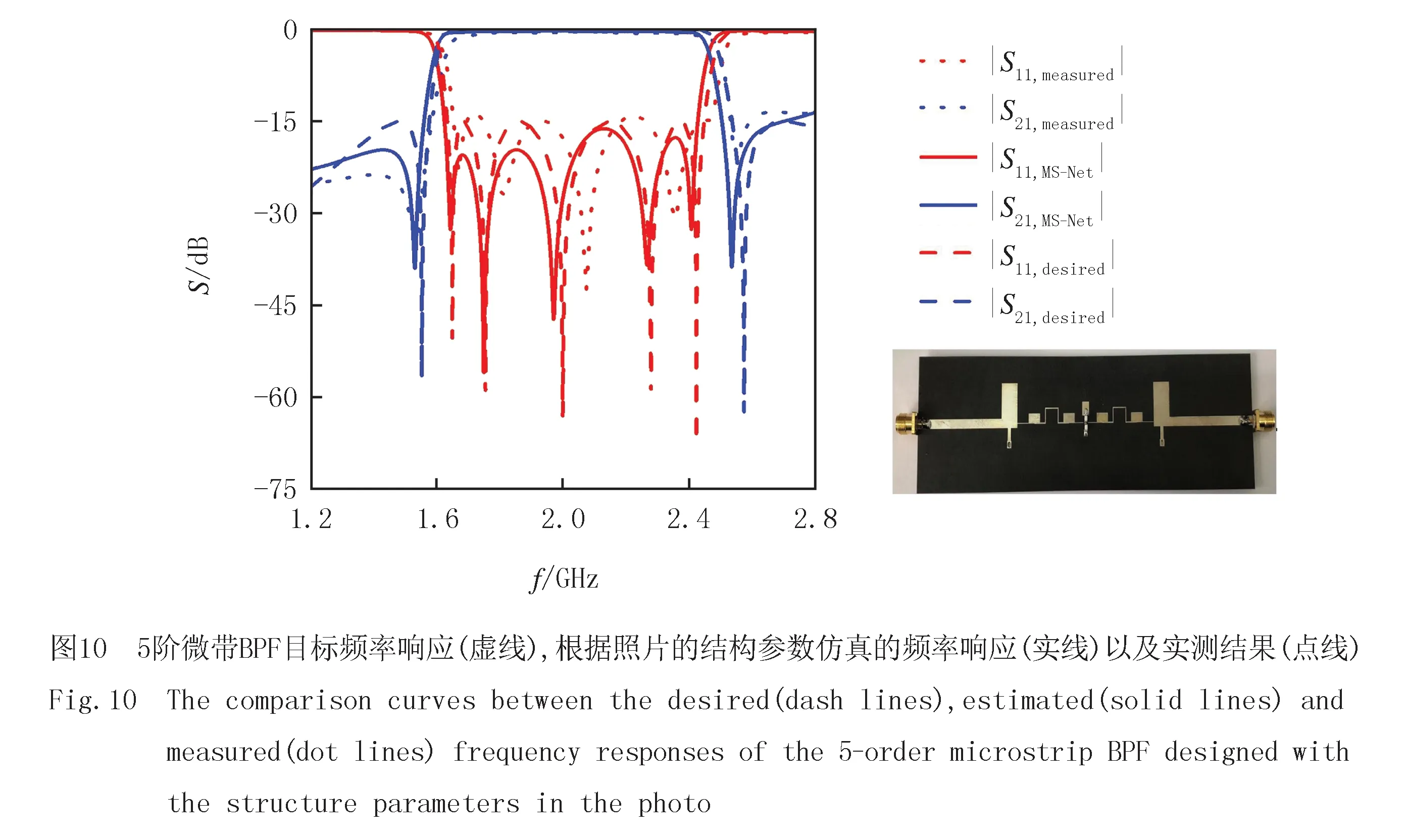
使用2个6层全连接网络作为MS-Net的主网络和子网络,每层的神经元数量如表6所示.目标S参数是根据理想滤波特性函数计算得到的.因为这个例子中需要估计的结构参数的数量相比3阶BPF更多,所以使用更多的网络层数和更多的神经元.在3.5 h内得到一组满足设计要求的结构参数(见表4).为了实现该设计,使用介电常数2.65,厚度为0.1 mm的基板(图10).根据实验结果表明,采用该方法估计的结构参数设计的滤波器可以很好地达到预期的效果.
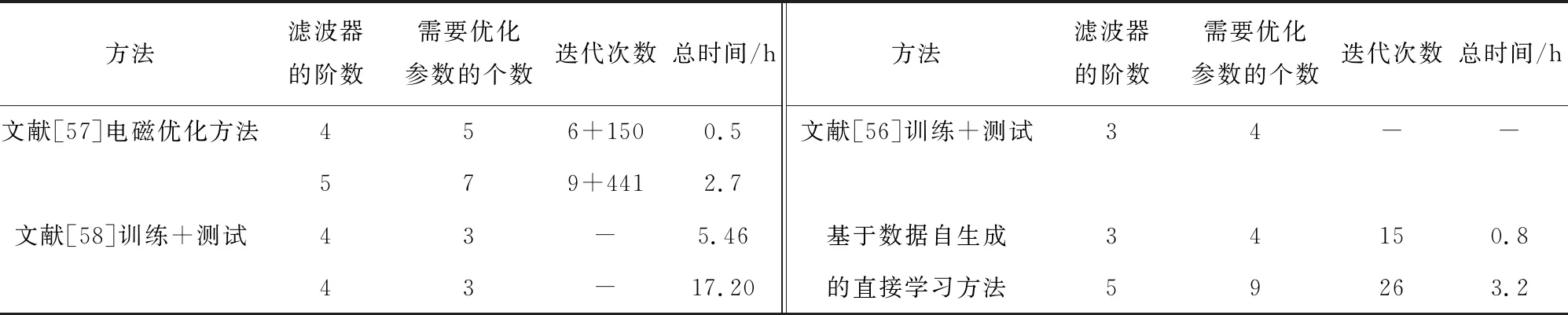
表6 不同优化方法的比较
这2个实验表明,提出的基于数据自生成的结构参数估计方法可以有效地根据滤波器的目标S参数估计结构参数.最先进的优化方法与本工作的比较见表7.除了使用理想的S参数作为神经网络的输入外,阈值和置信区间也可以作为神经网络的输入.该子网络能够在每个学习步骤中使用主网络的生成数据,不需要额外的收集数据集,可以省去网络预训练的工作,减少时间成本.
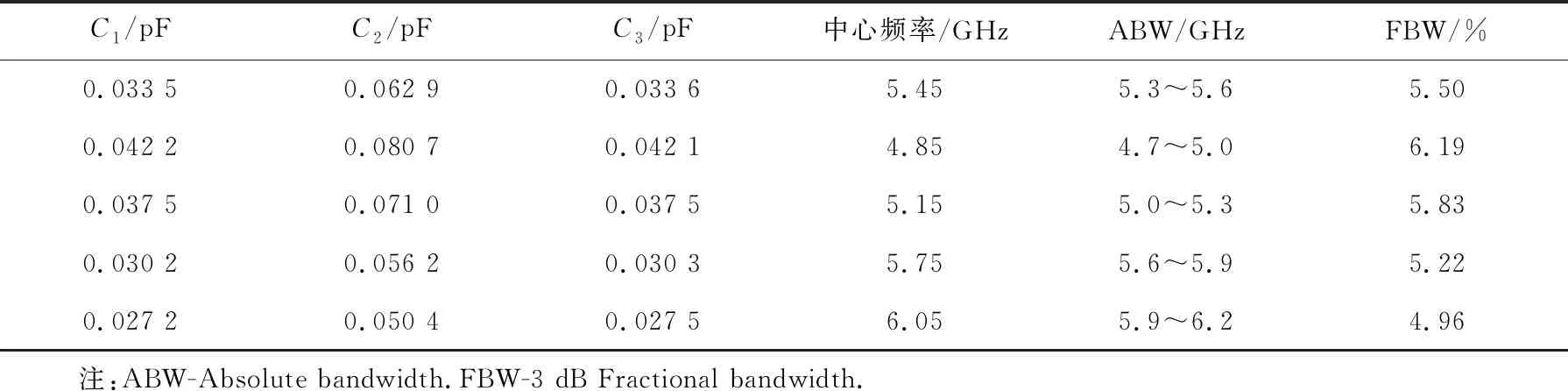
表7 不同中心频率、ABW和FBW范围下的电容
3.3 基于神经网络的带宽可重构滤波器设计方法
可重构滤波器是无线通信系统的重要组成部分.可以实现可重构功能的方法包括半导体变容管、射频微机电系统等[59-60].此外,一种基于集总元件的可调滤波器[61],由串联LC和阻抗逆变器组成.使用分支线型谐振器的3比特可重构带通滤波器[62],可以实现低插入损耗.为满足不同系统的需要,提出一种可调通带边缘和带宽的可重构带通滤波器,可以使2个通带独立可调[63].通过选择谐振腔上负载变容二极管的特定位置,设计一种具有恒定绝对带宽的高选择性可调谐平衡带通滤波器[64].首次设计了一种中心频率、带宽和零点控制的3极可调组合带通滤波器[65].
不同于上述的可重构滤波器设计方法,提出一种基于神经网络的带宽可重构滤波器设计方法[66].采用集总元件电路设计可重构BPF,电路由5个串联LC电路组成.3个串联支路可以提供3个传输极点,而2个并联支路可以引入2个相同的传输零点.利用神经网络优化LC电路的电感和电容值来达到中心频率可调、绝对带宽恒定的设计要求.单次参数优化可在30次迭代内完成.
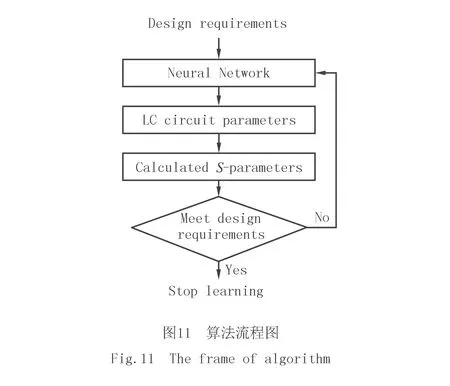
具体包括2个步骤.第一步是在确定的设计要求下优化LC电路参数(电容值和电感值).第2步是保持LC电路中的电感值不变,与第一步优化方法相同,但是只优化电容值,以达到恒定带宽改变中心频率的效果.这2个设计步骤中都采用3层全连接网络作为LC电路参数的优化工具.如图11所示的算法流程图,网络的输入是滤波器的设计要求,输出6个电路参数值.然后根据神经网络输出的LC电路参数值计算相应的S参数.以计算得到的S参数与设计要求之间的误差函数作为损失函数,更新网络权值.误差函数包含绝对带宽误差、回波损耗误差和中心频率误差,L=E(ABW,ABW′)+E(RL,RL′)+E(CF,CF′),其中ABW′、RL′和CF′分别表示满足设计要求的绝对带宽、回波损耗和中心频率,函数E是平均绝对误差.经过迭代学习之后,网络输出满足设计要求的电路参数值.
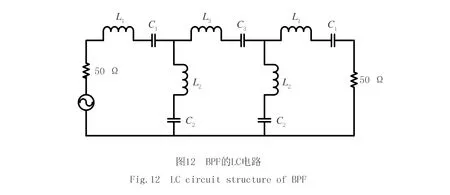
如图12所示,BPF的LC电路基于广义切比雪夫BPF[67]改进的对称结构,LC电路参数包括3个电感值L1、L2、L3和3个电容值C1、C2、C3.这个电路是对称的,3个串联支路(L1和C1,L3和C3,L1和C1)实现3个传输极点,传输零点是由L2和C2在其共振频率处的并联的串联支路短路引起的.
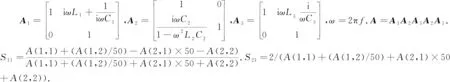
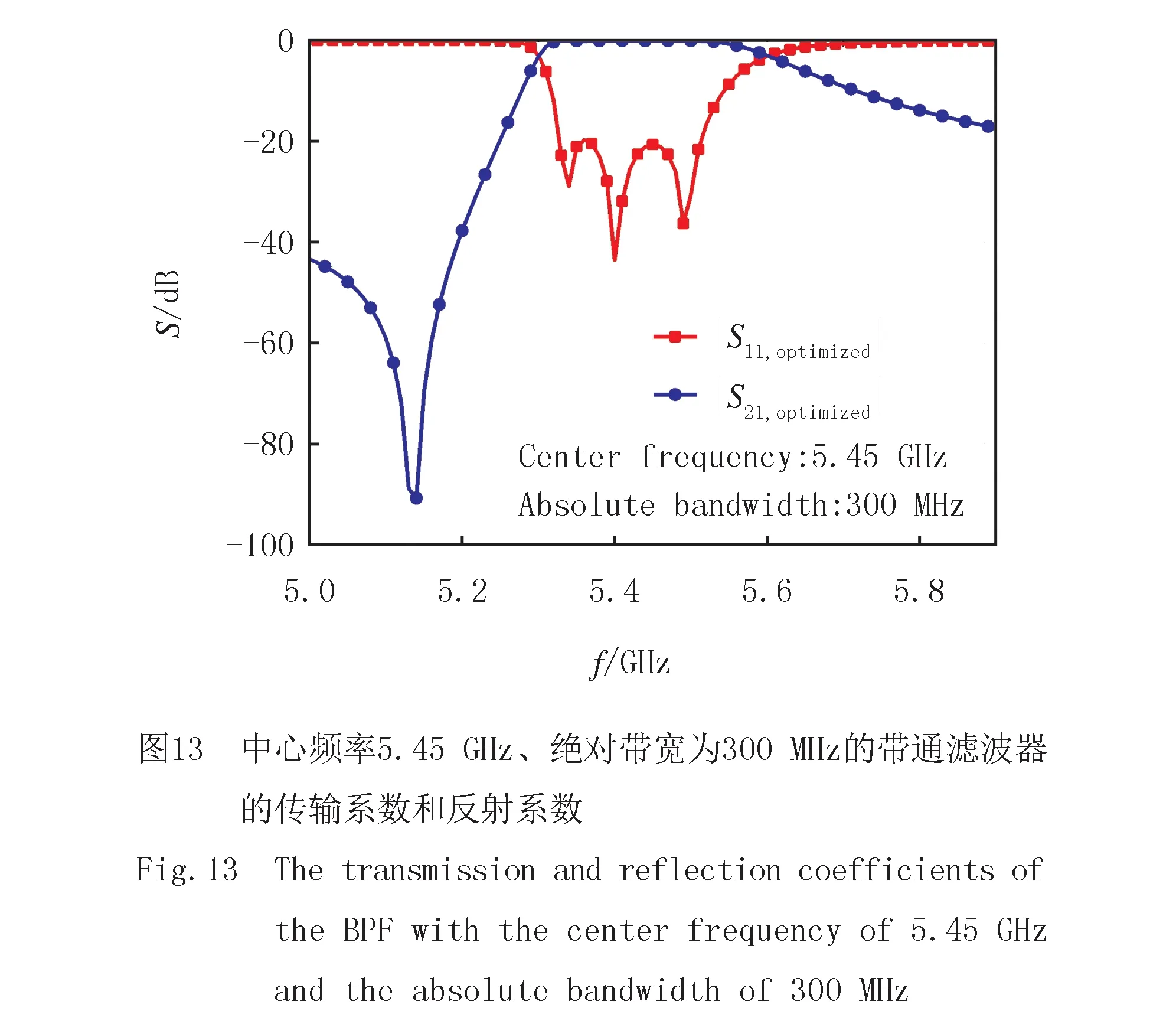
为了验证该方法,设计一种适用于高速数据通信的可重构带通滤波器.设计要求:绝对带宽300 MHz, 回波损耗20 dB,中心频率5.45 GHz.优化出一组满足要求的参数值:C1=0.033 5 pF,C2=0.062 9 pF,C3=0.033 6 pF,L1=24.85 nH,L2=15.27 nH,L3=23.65 nH.对应的频率响应如图13所示,满足设计要求.
在可重构滤波器设计中,由于电感值不能调节,因此仍然使用第一步得到的3个电感值保持不变,只优化3个电容值.对绝对带宽和回波损耗的要求与前面相同.中心频率要求为4.85~6.05 GHz之间的一个频率点,间隔0.3 GHz.在绝对带宽为300 MHz时,不同中心频率下的频率响应如图14所示.优化得到的满足设计要求的3组电容值、绝对带宽和分数带宽的范围分别列在表8中.每组电容值在30次迭代内得到.
以上实验结果表明,绝对带宽为300 MHz的可重构带通滤波器,其中心频率可在0.6~0.8 GHz(5.45~6.05 GHz)之间调谐.这种基于神经网络的可重构滤波器设计方法能够在相同ABW、不同中心频率的情况下,有效、准确地优化满足设计要求的多个BPF的 LC电路参数,证明了该方法的有效性.这种方法将深度学习方法应用于可重构滤波器设计领域,验证了深度学习方法可应用在不同的微波器件设计中,加快设计速度和提高设计效率.
4 结 论
本文描述了神经网络的基础模型结构和常用的训练方法,从传统神经网络建模方法、基于极限学习机的设计方法、基于知识神经网络的设计方法、神经网络和传递函数相结合的设计方法这4个方面对基于神经网络的优化算法在微波器件领域中的应用进行综述和比较,阐述了在微波器件设计中引入基于神经网络优化方法的优势.基于此,提出3种基于神经网络的带通滤波器设计方法:
1)基于训练和精调的神经网络方法,在双通带滤波器的LC电路参数提取任务中,利用滤波器S参数的相位信息在短时间内获得不同阶数、不同中心频率、不同带宽的最优电路参数.
2)基于数据自生成神经网络的带通滤波器结构参数估计方法,有效地根据滤波器的目标S参数估计出最佳的滤波器结构参数,无需网络的预训练过程,缩短了设计时间.
3)带宽可重构的带通滤波器设计方法,可以在较短时间内准确的设计出相同绝对带宽、不同中心频率的带通滤波器.
这些方法验证了基于神经网络的优化方法可以应用于不同的微波器件设计任务,不仅可以获得较高的设计精度,还能降低数学复杂度、加速设计速度,有效降低设计成本.
