基于流固耦合的液环泵转子动力学特性分析
2023-10-31吴港永张人会芦维强陈学炳
吴港永,张人会,2,芦维强,陈学炳,2
(1.兰州理工大学 能源与动力工程学院,兰州 730050;2.甘肃省流体机械及系统重点试验室,兰州 730050)
0 引言
液环泵是一种用来抽送气体的流体机械,常用于抽吸和压缩易燃易爆、含粉尘、有毒性的气体,由于其具有大流量、等温压缩、转子与泵体无接触等特点,被广泛应用于石油、煤矿、化工及核电等领域[1-7]。在叶轮的高速旋转作用下,液环泵内气液两相流动近似呈气液分离状态,其气液分界面呈不规则的锯齿形[8],由于叶轮偏心地安装于壳体中,叶轮及壳体内气液两相流动在周向呈非对称特性,叶轮旋转时,液环泵转子受非稳定应力作用导致转子运行稳定性变差[9-11]。目前,对于液环泵内非稳态气液两相流动的分析[1-5,8]及其叶片与壳体型线的水力优化[2,6,10-11]已经做了大量的研究工作,但对于泵内非稳态气液两相流动引起的转子结构响应特性分析尚无相关进展。对于流固耦合分析是当前流体机械领域研究的热点之一[12-17],滕爽等[18]结合单向流固耦合方法,分析了多级冲压泵转子部件的等效应力、变形量分布情况,发现最大等效应力出现在轮毂处,最大变形量则出现在叶片外缘处;袁寿其等[19]发现考虑流固耦合作用后,泵进口处的压力波动加剧,出口压力波动强度降低;江伟等[20]分析叶轮流固耦合作用对其内部流场的影响,发现流固耦合作用对流场计算结果的影响的确存在,而且规律较为复杂。目前随着液环泵应用领域的拓展,在核电、航空航天等领域的应用对其运行稳定性提出了更高的要求,但目前针对液环泵转子动力学特性的分析却少有相关研究报道。
本文采用ANSYS软件对液环泵的转子部件进行流固耦合计算分析,分析转子的应力及变形沿圆周方向的分布特征及其非稳态特性,分析叶片上的应力及变形量的分布特征,分析转子的模态特性,期望为液环泵的结构优化设计提供一定理论参考。
1 数值计算
1.1 研究对象和网格划分
以2BEA-202型液环泵为研究对象,其主要参数见表1。

表1 2BEA-202型液环泵主要参数Tab.1 Main parameters of 2BEA-202 liquid ring pump
固体计算域由叶轮和泵轴组成,流体计算域由吸气口、排气口、叶轮和泵壳体组成,创建固体计算域和流体计算域的三维模型。使用ANSYS ICEM软件对流体计算域进行六面体结构网格划分,液环泵计算域各部分网格如图1所示,经过网格无关性验证,最终确定的网格数量为262万。使用ANSYS 软件对固体计算域进行了四面体非结构网格划分,固体计算域各部分网格如图2所示,固体计算域的网格数量为11万。
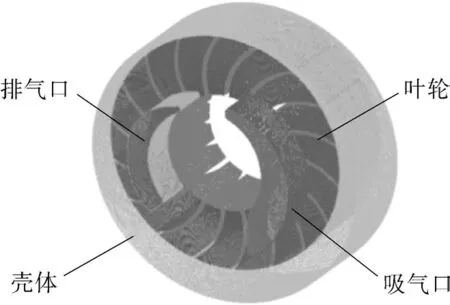
图1 流体计算域网格Fig.1 Computational domain grids of fluid
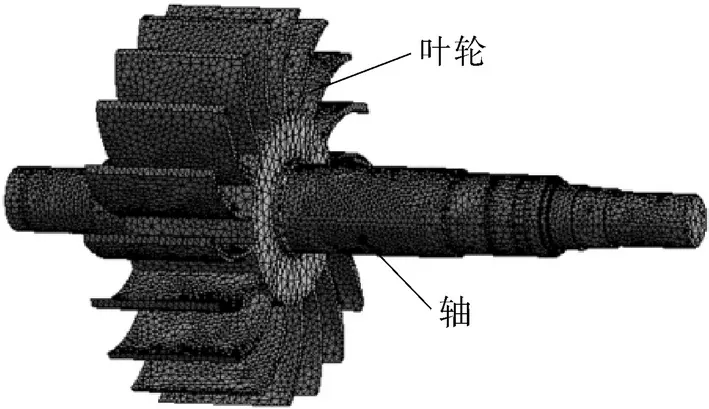
图2 固体计算域网格Fig.2 Computational domain grids of solid
流体介质为可压缩空气和常温清水,固体计算域中的泵主轴和叶轮的材料分别为45号钢、304不锈钢。
1.2 流场边界条件
利用ANSYS FLUENT软件对液环泵内的流动进行数值计算。选择RNG k-ε湍流模型与VOF气液两相流模型,进口边界条件设置为质量流量进口,出口边界条件为压力出口,壁面采用的是无滑移边界条件,计算过程中采用PISO压力速度耦合算法,压力项、湍动能项以及相态体积分数项均采用一阶迎风格式,时间步长定义为Δt=2×10-5s。利用流固耦合求解器System Coupling进行流场与结构场的耦合求解。在瞬态结构场计算时,时间步长的设置与流场计算中一致。
1.3 载荷与约束
轴承接触的两侧轴面上添加圆柱面约束(A,B),轴与电机的连接端添加固定约束(E),对整个转子部件添加离心载荷和自身重力(D,C),通过流固耦合交界面将内流场的载荷传递到叶片表面(F),载荷与约束分布如图3所示。
1.4 试验装置及方法
为了验证数值模拟的准确性,采用如图4所示的试验装置对液环泵的外特性进行测量,该试验台主要由液环泵、电机、进出气口管路等组成。
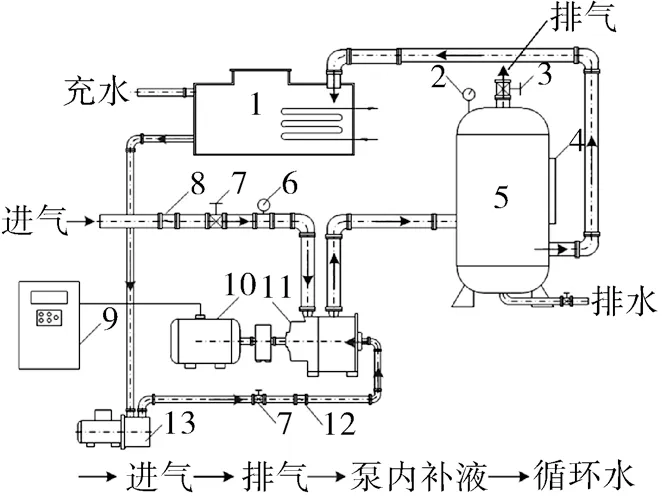
图4 液环泵试验系统Fig.4 Experimental system diagram of liquid ring pump
液环泵效率的计算式为:
式中,Qv为液环泵进口的气体体积流量;p1,p2分别为液环泵的进、出口压力;p为输入功率。
由进口压力传感器测得p1,其测量范围为-100~0 kPa,精度为0.5%,p2为大气压力,p由控制柜采用电测法测量,Qv由孔板流量计测量,其中的压力变送器测量范围为0~40 kPa,泵壳体动态压力传感器型号为CY100,其精度为±0.25%FS,量程为0~0.8 MPa。通过调节进气阀来改变液环泵的进口气体体积流量,进而对各工况点的数据进行测量。
2 计算结果与分析
2.1 液环泵的外特性分析
图5示出液环泵水力性能的数值模拟与试验结果对比分析,由图中可以看出,二者数值基本吻合,液环泵的进口压力随着质量流量的增加而增加,效率则呈现出先增加后减小的变化趋势。各流量工况点的效率及进口真空度的模拟值均高于试验值,真空度的预测值在大流量点有一定的偏差,在0.05 kg/s工况点效率的模拟值和试验值分别为14.8%,11.2%,预测偏差为3.6%,其主要原因是在数值计算时忽略了叶轮轴向端面间隙泄漏流动,未考虑间隙泄漏损失,且由于网格分辨的限制,部分小尺度流动结构引起的损失无法预测。由上可知,本文模型具有良好的计算准确性。
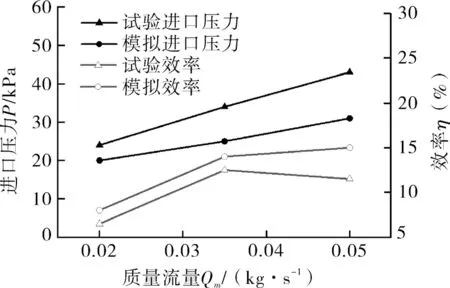
图5 液环泵数值模拟与试验结果对比Fig.5 Comparison between numerical simulation and experimental results of liquid ring pump
液环泵内轴垂面上的相态及压力分布如图6所示,泵内气液两相流呈气液分离状态,气液交界面近似呈锯齿形分布;泵内压力沿半径方向逐渐增大,在气液交界面存在较大的压力梯度。
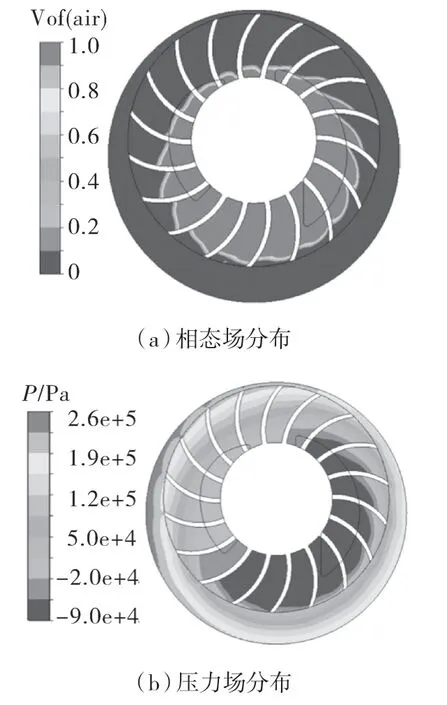
图6 液环泵内相态及压力场分布图Fig.6 Distribution of phase state and pressure field in liquid ring pump
2.2 转子部件的应力应变分析
2.2.1 转子部件最大等效应力和最大变形量随旋转角度的变化
叶轮高速旋转使液环泵内产生复杂的非稳态气液两相流动结构,由于叶轮出口流动的不均匀性导致泵内流动的不稳定性,引起叶轮及壳体应力的脉动。以图7示出的叶片18正对y轴正半轴为基准,定义α为叶轮叶片旋转角度。
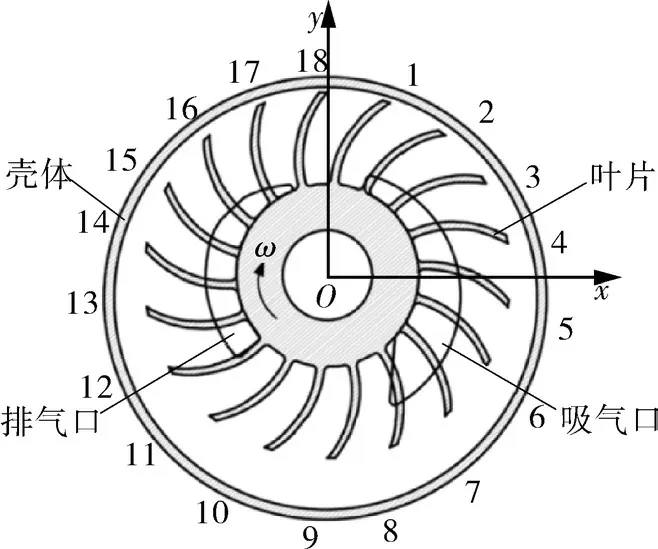
图7 叶片与蜗壳相对位置Fig.7 Relative position of blade and volute
由于叶轮旋转引起叶轮及壳体应力应变呈一定周期性脉动,对不同流量工况下α=0°、4°、8°、12°和16°时转子部件进行应力应变分析。转子部件最大等效应力σmax及最大变形量Smax随叶轮旋转角度α变化如图8所示。
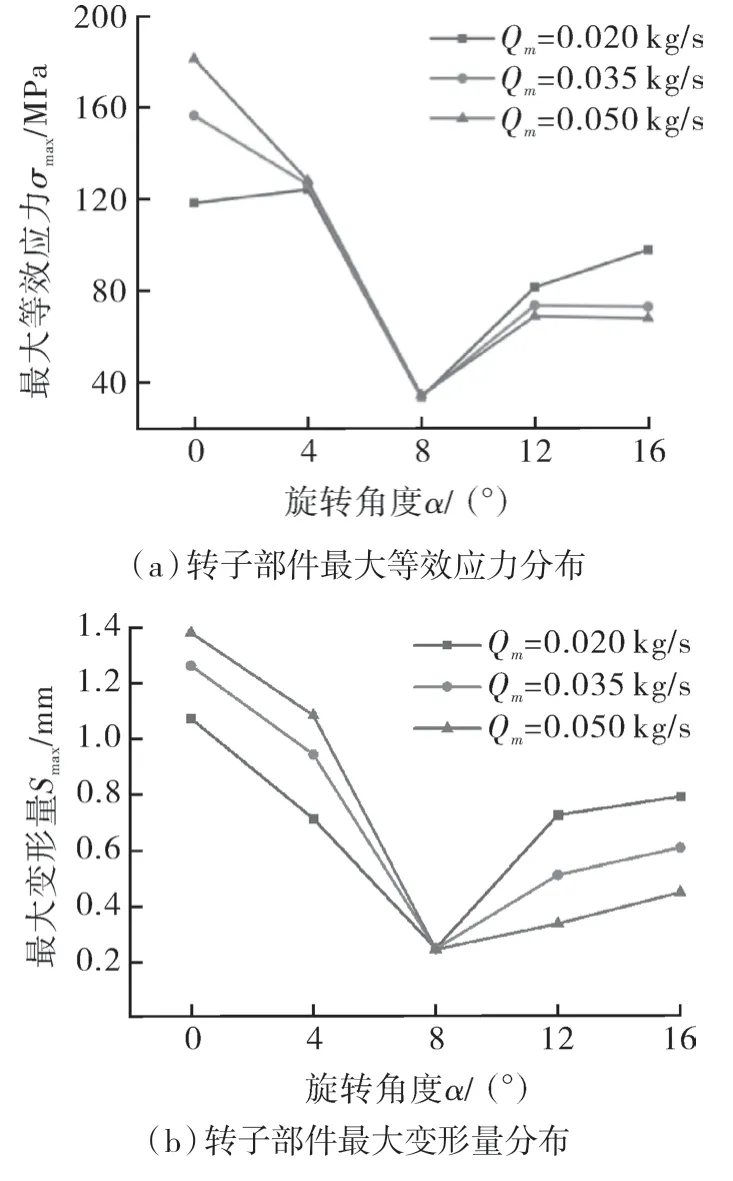
图8 转子部件应力应变分析Fig.8 Stress and strain analysis of rotor components
由图8可以看出,在一个叶片夹角的旋转周期内(α=0°~20°),随着旋转角α的增大,最大等效应力先减小后增大,当叶片尖部与壳体内壁距离最小时(α=0°)的最大等效应力为最大值;转子最大变形量随转角α的变化趋势与最大等效应力的变化趋势完全一致;转子的最大等效应力及最大变形量均呈周期性脉动。当α=8°叶片最大变形量及最大等效应力值均达到最小,此时由于叶片17与18之间的中间位置正好旋转到壳体顶部,叶片与壳体间的最小距离最大,相对径向间隙为最大值,叶片与壳体相对位置的变化引起叶片载荷的变化。
2.2.2 不同叶片的最大变形量沿圆周变化
当旋转角度α=0°,流量Qm=0.050 kg/s时,转子部件最大等效应力及最大变形量为最大值,对该工况下叶轮18枚叶片的最大变形量进行分析,如图9所示。从图中可以看出,叶轮旋转角从0°~16°变化时,18枚叶片的最大变形量整体上先减小后增大,旋转角为8°,12°和16°时各叶片的最大变形量比0°和4°时的最大变形量下降明显。变形量较大的叶轮旋转角0°和4°时,叶片最大变形量从吸气区始端(叶片18)开始逐渐减小至压缩区始端(叶片10),从压缩区始端(叶片10)到排气区末端(18)叶片最大变形量逐渐增大。
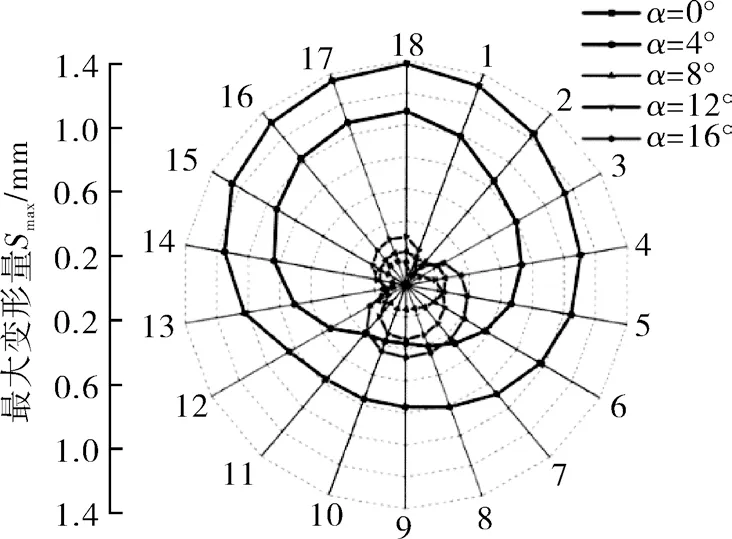
图9 不同叶片上最大变形量分布Fig.9 Distribution of maximum deformation on different blades
2.2.3 叶片的应力应变分布规律
由上述分析可知,叶片应力分布沿周向变化,α=0°时,叶轮叶片18的变形量最大,具体分析每个叶片上的应力分布,选取应力最大的叶片18进行应力应变分析。为了分析叶片上的应力及变形量变化规律,对叶片的4条边界线(a,b,c,d)定义如图10所示,分别分析4条边界线上的应力及变形规律。
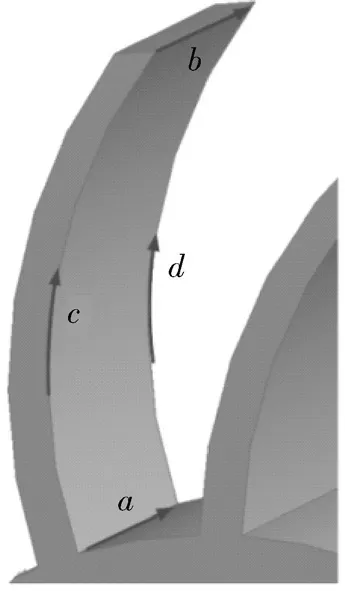
图10 轴向和径向方向的路径Fig.10 Axial and radial paths
通过静力学分析可得叶轮叶片选取位置上的变形量分布规律,如图11所示,横坐标为边界线上的无量纲的距离,可以看出沿轴线方向路径a,b,变形量基本保持不变,沿径向方向路径c,d,从轮毂到叶片顶部,径向方向的变形量近似线性增大。为进一步计算叶片18的强度是否符合工程实际,给出了该叶片沿轴向和径向方向的等效应力变化规律,如图12所示。从图中可以看出,径向方向的等效应力呈现出先急剧增加后缓慢减少的趋势,且在0.1r2位置处达到最大值,沿轴向方向的平均等效应力几乎保持不变,但越靠近叶片根部,等效应力的波动幅值越大。
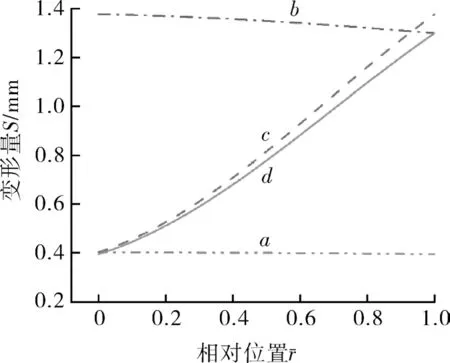
图11 轴向和径向方向的变形Fig.11 Deformation in axial and radial directions
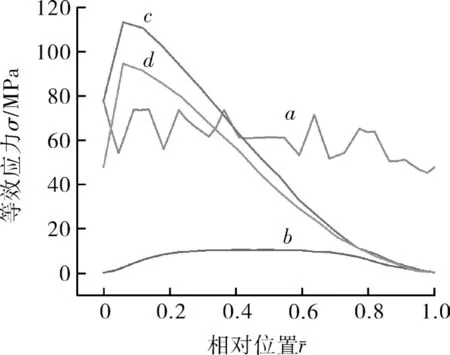
图12 轴向和径向方向的等效应力Fig.12 Equivalent stresses in axial and radial directions
2.3 转子部件模态分析
通过求解液环泵转子部件动力学方程得到其各阶模态固有频率及其振型。由于前几阶模态对转子运动起主导作用,考虑到液环泵的振动主要发生在中、低频段[21-22],因此本文选取液环泵转子部件的前6阶模态进行分析。
图13示出当Qm=0.050 kg/s工况时液环泵转子部件前6阶模态振型。从图中可知,第1阶模态振型为叶轮绕着旋转轴的扭动变形。转子部件的第2,3阶模态振型模态相似,均以摆动变形为主,不同的是两者摆动方向不一样,正好相差90°,即第2阶振型为沿x轴方向摆动,而第3阶模态则是沿着y轴方向摆动。第4,5,6阶模态振型同样比较相似,都是叶轮部分叶片绕旋转轴的摆动,不同之处是每次发生摆动的叶片有差异。

图13 转子部件前6阶模态振型Fig.13 The first six-order modes of rotor components
图14示出在不同流量下转子部件前6阶固有频率变化情况。从图中可看出,转子部件的第1阶固有频率最小,其值为145.6 Hz;第2阶与第3阶模态频率相近,这主要是由于液环泵转子部件属于对称结构,模态解耦过程中出现重根模态,也就是说第2阶与第3阶模态频率相同,相位之差为90°,图14中的振型恰好印证了这个观点。第4~6阶固有频率差别不大,其值约等于665 Hz,主要是因振动方式相同导致的。
从图15可以发现,第3,4阶振幅的变化最为剧烈,幅值变化高达38.1 mm,这主要是转子部件的振动变形方式存在很大差异。第2阶和第3阶振幅比较接近,此时转子部件的振型相近,相位相差90°。不同的流量下,转子部件前6阶固有频率和振幅变化不大,因此对液环泵转子部件进行模态分析时可以不用考虑流量对模态性能的影响。
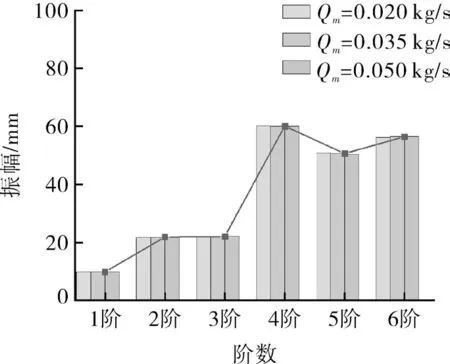
图15 不同流量下转子部件前6阶振幅Fig.15 The first six-order amplitudes of amplitudes under different flow rates
液环泵在运行时,其内部非定常流动而产生的压力脉动特性是引起结构振动的重要因素。当压力脉动的激励频率(叶频和二次倍频)与转子部件的固有频率接近重合时,转子部件会发生共振,对液环泵的稳定运行产生重大影响。因此,在液环泵稳定运行时,转子部件的固有频率要尽量远离叶频与二次倍频。研究的液环泵转速n=1 450 r/min,叶片数Z=18,液环泵叶频和二次倍频分别为435.1,870.1 Hz。由图14可以看出,第1阶固有频率比叶频低约为290.0 Hz,第2~6阶固有频率介于435.1~870.1 Hz之间,但明显远离叶频和二次倍频,因此液环泵转子部件不会发生共振。
3 结论
(1)由于叶轮出口流动的不均匀性及叶轮流场的周向非对称特性,转子的最大等效应力及最大变形量随叶轮旋转呈周期性脉动。在一个叶片夹角的旋转周期内,随着旋转角的增大,最大等效应力先减小后增大,当叶片尖部与壳体内壁距离最小时的最大等效应力为最大值;转子最大变形量的随转角的变化趋势与最大等效应力的变化趋势完全一致。
(2)叶轮沿圆周方向18枚叶片上的最大应力分布各不相同,且其随着叶轮旋转角从0°到16°变化时,18枚叶片的最大变形量整体上先减小后增大。
(3)叶片上的变形量分布沿径向由轮毂到叶尖近似呈线性逐渐增大,应力沿径向方向先急剧增加后缓慢减少,且在0.1r2位置处达到最大值。叶片上的应力及变形沿轴线方向基本保持恒定。
(4)流量对转子部件的固有频率及振幅影响很小,转子部件的第1阶固有频率比叶频低约290.0 Hz,第2~6阶固有频率介于叶频和二次倍频之间,由此表明液环泵转子部件不会发生共振。
