家用空调系统管路应变分析及优化
2023-10-31秦永强胡远培
郭 蘅,秦永强,廖 熠,胡远培
(1.空调设备及系统运行节能国家重点实验室,广东珠海 519070;2.珠海格力电器股份有限公司,广东珠海 519070)
0 引言
目前我国制冷、空调技术正处于快速发展阶段,提高产品的可靠性成为整个空调行业的基本要求。空调系统由于自身激励和结构设计的原因,在运行中不可避免会发生振动[1-4]。长期剧烈振动作用,会导致应变超标,产生疲劳,进而导致寿命降低,因此改善空调系统应变问题很有必要[5-6]。空调管路系统运行过程中,当忽略其内部流体压力脉动影响(家用小型空调系统内部流体压力脉动有限)时,其应变过大主要由以下3个方面原因导致:(1)内部的压缩机振动激励过大,带动管路振动、应变过大;(2)压缩机自身振动激励不明显,但管路自身固频与压缩机运行频率重合,形成共振,导致管路应变过大;(3)压缩机本身激励不大,管路也无共振频率,但管路系统走向紧凑、刚度过大,运行中应力集中导致应变过大。在当前压缩机技术日益成熟的条件下,后两者占大多数[7-10]。因此,通过仿真手段,对空调管路自身动态特性和应力应变进行相应的研究,并在设计阶段精准预测超标与否和识别超标原因,布置合理的管路走向,对提高管路寿命和可靠性具有重要意义。
蒋邹等[11]对空调外机管路进行了有限元仿真、模态和应力测试研究。但因其未建立准确的压缩机模型,部分仿真结果与试验结果差异较大。王枫等[12]建立了含有简化压缩机结构的系统模型,并针对空调管路振动问题,提出了优化设计方法,但未对仿真结果进行试验验证。章兰珠等[13]建立了含有简化压缩机结构的系统模型,且对其模态仿真结果进行了试验验证,但未对其振动响应结果进行实测。丁一[14]采用简化压缩机结构建模,且用试验验证了空调管路模态分析结果和谐响应分析结果,但未提出改进方案。沈慧等[15]采用简化压缩机结构建模,将测试所得减振垫圈刚度数值代入模型提高管路谐响应仿真精度,但在未对降低应力应变提出改进方案。单国伟等[16]在仿真建模过程中未建立压缩机结构,仅通过改变空调管路长度,来改善管路模态特性。黄辉等[17]通过仿真分析,仅研究了不同管路折弯厚度对模态的影响,付永领等[18]仅研究了弯管转角对该管道振动特性的影响。
当前相关研究,仿真模型不够精确(未建立压缩机模型或未考虑脚垫)、未进行试验验证、仅有模态分析(未进行谐响应分析)、未提出改进方案、未针对仿真结果详细分析而仅改变某单一因素(管路长度、厚度、转角等)进行验证。均未能包含完整的高精度建模(包含压缩机结构,并考虑脚垫)、模态和采用真实载荷的谐响应仿真、模态和应变测试、针对仿真和试验进行详细原因分析、针对分析结果提出改进方案、改进方案仿真和验证的过程。在实际研发过程中,对于管路应变超标问题,需针对实际原因具体分析,仅仅通过改变单一因素(如管路长度、壁厚或转角等)很难改善。
本文针对某家用单冷空调系统,进行了基于精确模型和真实载荷的模态和谐响应分析,提出两种改进方案,并通过试验对两种改进方案进行验证。
1 模态分析和谐响应分析理论基础
模态计算是分析所有系统动力学特性的基础。系统的固有频率和模态振型等,均可通过模态计算得到。模态分析和改进,可使系统避开共振频率。
在动力学分析中,空调管路系统可看作一个多自由度振动系统,控制微分方程为:
当不考虑系统阻尼和外力时,式(1)可简化为:
假设结构的运动为简谐运动:
将结构运动的位移和速度,代入到控制方程(2)中,可得:
对式(5)进行求解,可得到n个方程的根,这些根是其特征值。对于每一根(特征值),都对应着一个特征向量,求解即可获得系统的固有频率和对应的特征向量,也即系统的模态。
谐响应分析是确定机械结构在已知频率的正弦(简谐)载荷作用下结构响应的技术。输入已知大小和频率的谐波载荷(力、压力或强迫位移等),可输出每一个自由度上的谐位移及其他多种导出量,例如应变等。当激励频率靠近激励方向的结构固有频率时,结构会发生共振现象,响应出现峰值。谐响应分析常用于设计含有旋转设备的机械系统,故可用来计算含有压缩机(旋转设备)的空调管路系统在特定频率(段)下的应变值。
谐响应主要有两种求解方法,完全法和模态叠加法。模态叠加法通过使用具有正交关系的模态振型向量的线性组合来对谐响应分析控制方法进行解耦计算,一般情况下,求解速度快于完全法。其求解频率点可均布在整个频率求解域中,也可在结构的固有频率处产生非均匀分布,即集中分布。
本研究利用ANSYS对系统进行模态仿真,并基于模态叠加法对管路进行谐响应仿真,关注管路系统的模态和应变结果。
2 原系统仿真与试验结果
2.1 原系统仿真结果
某家用单冷空调系统,搭载某小型定频转子压缩机,压缩机运行频率47.5 Hz。原系统整体结构及关注的测点位置如图1所示。开发过程中,投入试验前,利用ANSYS对系统进行模态仿真分析。

图1 原系统方案Fig.1 Original scheme
2.1.1 几何模型
几何模型,包括详细的压缩机外部结构(压缩机脚垫在仿真过程中可用弹簧代替,不必建立实体)和空调管路(空调吸气管路和排气管路)。
2.1.2 材料
压缩机吸气管、排气管和空调管路所用材料为铜;其余零件为结构钢。材料属性见表1。

表1 材料属性Tab.1 Material properties
2.1.3 载荷计算
谐响应计算过程中,所加合力矩为3 500 N·mm(根据压缩机实际受力分析结果,由内部开发软件计算得到)。
2.1.4 仿真结果
系统管路的固频仿真结果见表2,由其可知,管路存在与压缩机基频接近的频率为46.078 Hz(图2示出该频率下的模态振型),可能会在基频发生共振。
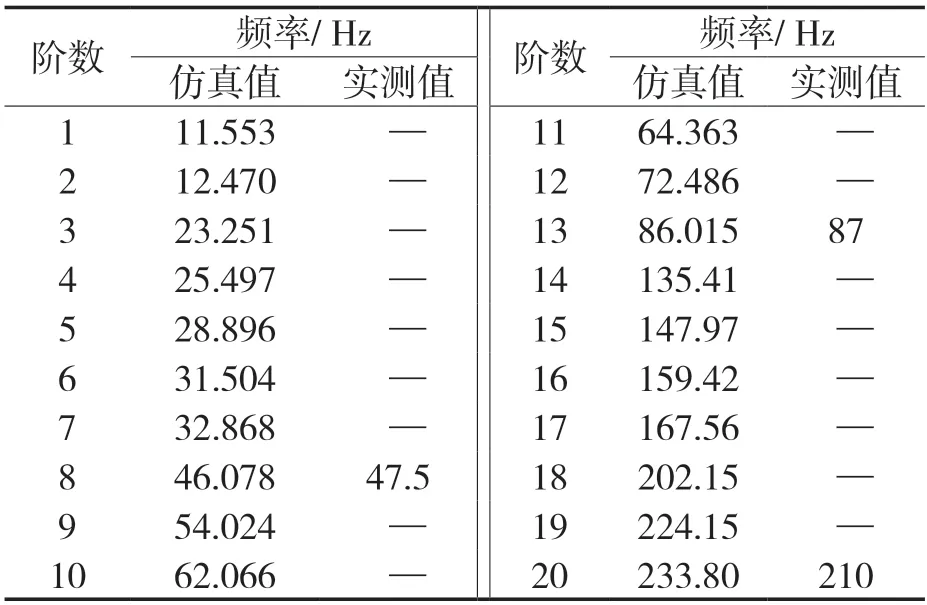
表2 原系统固有频率仿真值与测试值结果Tab.2 Simulation and test results of the natural frequencies of the original system

图2 原管路在压缩机基频附近的模态振型(46.078 Hz)Fig.2 Mode shape of the original pipeline near fundamental frequency of compressor(46.078 Hz)
同时对系统进行基于模态叠加法的谐响应仿真分析,结果如图3所示。可见,管路结构在基频处最大应变值,位于吸气管路弯头处,基频为111.65 με,预测试验结果远超应变测试标准。

图3 原管路基频(47.5 Hz)应变仿真结果Fig.3 Simulation results of the strain of original pipeline at fundamental frequency(47.5 Hz)
2.2 原系统试验结果
为确定当前仿真与试验结果的误差,以便后期利用仿真对管路系统进一步优化,故对系统进行模态和应变测试分析,并将测试结果与仿真结果进行对比。
2.2.1 测试方案
模态测试流程如图4(a)所示,所用设备为LMS Test.Lab数据采集系统、力锤和三向加速度传感器;应变测试流程如图4(b)所示,所用设备为多通道应变及振动采集仪(型号:VS-DAQ 08)、双向应变片(电阻120Ω,灵敏度 2.14)。

图4 管路测试流程Fig.4 Test flow chart of the pipeline
2.2.2 测试结果
模态测试结果与仿真结果对比见表2;原系统运行过程中应变测试结果如图5所示。

图5 原系统和改进方案Ⅱ应变实测结果Fig.5 Strain test results of the original pipeline and improved scheme Ⅱ
由表2可知,管路系统确实存在压缩机基频为47.5 Hz附近模态,且试验显示频率为47.5 Hz与仿真结果46.078 Hz一致,两者相差小于2 Hz,误差小于2.99%。
由图5可知,系统运行过程中,实测应变最大值达到109 με,远大于应变标准;且管路系统应变最大位置处于吸气管第一弯处。对比系统的应变仿真结果(图3,111.65 με)可知,应变仿真值与试验值相差2.65 με,误差小于2.37%。且仿真与试验显示的最大值位置一致。
综上所述,当前仿真方法准确度高(固频误差小于2.99%,应变误差小于2.35%),可预测试验结果。
3 对原系统分析改进
对原系统仿真和测试结果进行分析可知,其共振位置(见图2),并非应变值最大的位置(见图3,5)。因此,排气管路共振或吸气管路刚度过大是造成原系统应变超标的原因。
3.1 改进方案I
利用此仿真方法进行改进。首先从避开共振的角度出发,将排气管路减短了5 cm,如图6所示,以期改变排气管路模态,避开共振,进而降低应变。

图6 改进方案I基频(47.5 Hz)应变仿真结果Fig.6 Strain simulation results of improved scheme I at fundamental frequency(47.5 Hz)
仿真结果显示,其前20阶固频依次分别为12.262,13.614,24.009,25.938,29.689,32.005,53.863,57.079,61.143,62.01,72.113,73.531,85.149,104.7,110.3,180.32,194.35,229.28,233.94,243.66 Hz,均远离压缩机基频47.5 Hz。但管路系统应变最大值位置不变,且最大值为111.9 με(见图6),与原系统相比增加了0.25 με。改进方案I无效。
由此可知,造成此管路应变过大的主要原因非排气管路共振,而是因为吸气管路刚度过大。
3.2 改进方案Ⅱ
改进方案Ⅱ主要是从降低吸气管路刚度的角度出发,改变系统最大应变所在管路(吸气管路)的走向,主要降低吸气管路刚度,同时影响排气管路模态,避开共振频率。改进方案如图7所示。

图7 改进方案ⅡFig.7 Improvement scheme Ⅱ
3.2.1 改进方案Ⅱ仿真结果
模态仿真与试验结果见表3,此方案不存在47.5 Hz附近固频,距离压缩机基频最近的固频为38.174 Hz(振型见图8)和61.716 Hz(振型见图9),均远离基频。预测可避免共振。
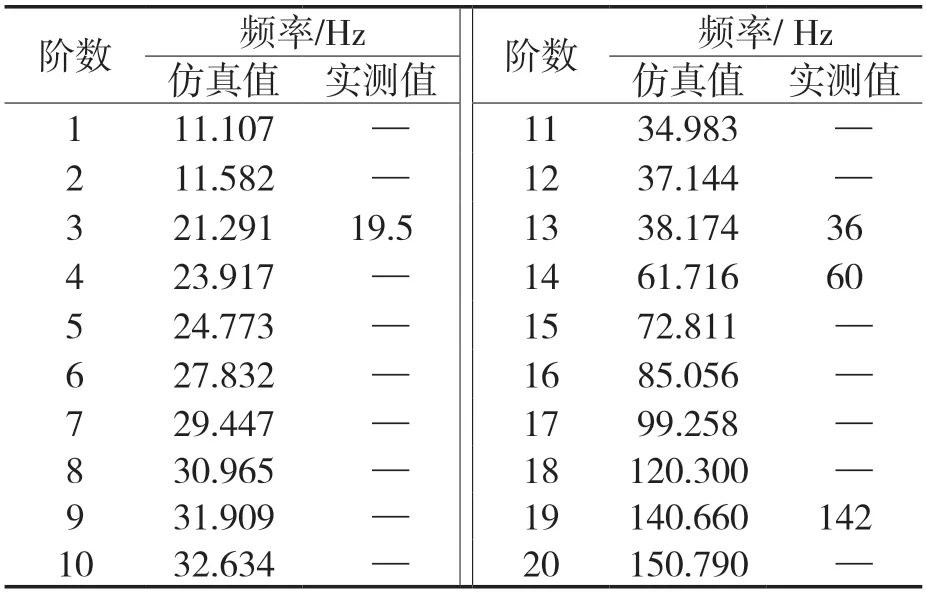
表3 改进方案Ⅱ固有频率仿真值与试验值结果Tab.3 Simulation and test results of the natural frequencies of improved scheme Ⅱ

图8 改进方案Ⅱ振型(38.174 Hz)Fig.8 Mode shape of improved scheme Ⅱ(38.174 Hz)

图9 改进方案Ⅱ振型(61.716 Hz)Fig.9 Mode shape of improved schemeⅡ(61.716 Hz)
同时,管路系统的整体应变仿真结果如图10所示,吸气管路(改进前最大应变出现的管路)应变结果如图11所示。仿真结果显示,管路最大应变转移到排气2弯处,仿真值为24.998 με;而吸气1弯处应变降低到19 με,预测可实现明显改善。
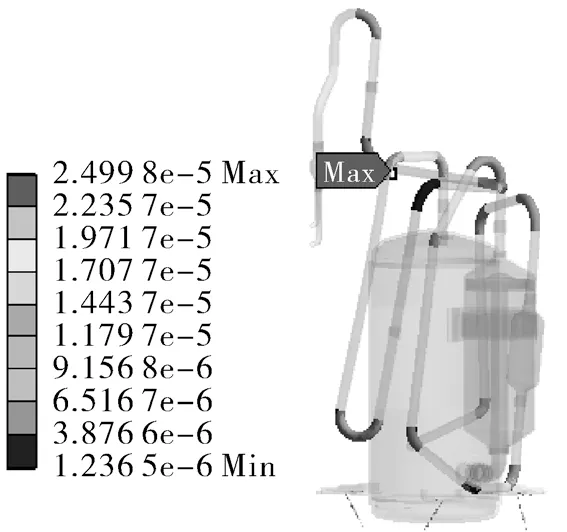
图10 改进方案Ⅱ基频(47.5 Hz)应变仿真结果Fig.10 Strain simulation results of improved scheme Ⅱat fundamental frequency(47.5 Hz)
3.2.2 改进方案Ⅱ试验结果
对改进方案Ⅱ进行验证,其管路模态测试结果对比见表3,应变测试结果如图5所示。
由表3可知,改进方案Ⅱ管路模态的确已经避开压缩机基频(不存在47.5 Hz左右模态),与仿真结果预测结果一致。
由图5可知,所有测点中应变最大值为27 με,与仿真结果(图10,24.998 με)误差为2.002 με;且最大应变位置与仿真结果一致,均位于排气2弯处。同时,原系统应变最大位置处(图3,吸气1弯),在改进方案中实测为20 με,与其仿真结果(图11,19.083 με)基本一致。再次证明此仿真方法准确度高,可精确预测试验结果。
同时,吸气1弯(20 με)与改进前相比(109 με),应变值降低89 με,降幅达到81.7%。充分证明,此仿真方法可用于分析改进空调系统管路应变问题。
此外,对比改进方案I和Ⅱ可知,家用空调管路应变问题,并非简单通过优化单一因素(如管路长度)就可改善;整体管路走向是影响此类问题的最关键因素;通过良好的布局,能有效避免共振及刚度过大的问题,进而改善应变。
4 结论
(1)本文仿真方法采用高精度建模(包含压缩机结构,并考虑脚垫)、谐响应分析采用压缩机真实载荷,准确度较高,管路固频仿真值与试验结果相差小于2 Hz,误差小于2.99%。管路运行应变仿真值与试验结果相差不超过3 με,误差最小可达2.37%。且仿真与试验显示的最大值出现位置一致。可用于精确预测试验结果。
(2)采用优化管路走向的方法可有效降低管路应变。应变最多降低89 με,降幅达到81.7%。
(3)整体管路走向,才是影响家用空调应改问题的最关键因素。针对仿真结果,分析具体原因,建立良好的管路布局,能有效避免共振及刚度过大的问题,进而改善应变。
(4)对家用空调系统管路动态特性和应变进行研究,在设计阶段精准预测试验结果,并识别应变超标原因,进而合理布置管路走向,提高空调系统可靠性,对提高产品品质具有重要意义。
