空调用前掠式轴流风叶优化
2023-10-31黄愉太
黄愉太
(佛山市云米电器科技有限公司,广东顺德 528000)
0 引言
常用的轴流式、离心式、横流式三大通风系统已广泛应用于各行各业,对于空调室外机散热通风系统,考虑其低噪声、大流量、高效率等需求,前掠式低压轴流风叶为其不二选择。作为空调外机的核心系统,长期以来轴流风叶的优化设计很大程度依赖于大量试验,开发成本高且周期长,尤其无法直观地分析风叶内流场特征,难以给出合理的优化方向。随着CFD,CAE等仿真技术的快速发展,轴流风叶也得以从气动性能及噪声特性等各方面进行系统和参数化研究,极大地提高了设计水平[1]。
空调室外机散热系统对轴流风叶效率和噪声要求非常高,良好的噪声表现可满足人们舒适体验,张伟捷[2]采用边界涡量流(BVF)对轴流风叶气动噪声进行了系统研究,对于轴流风叶的优化方向,现有文献主要集中于叶片安装角[3]、尾缘凹陷[4]、叶片弯掠[5]、截面型线[6]及风道系统匹配等[7-10]。众所周知叶片的弯掠形式对其性能最为重要,但现有文献对具体的叶片弯掠优化方法介绍较少,且研究内容未见系统性的风叶设计研究思路。
本文创新性地将轴流叶片切分为不同径向截面,通过调整各径向截面角度,重构为不同弯掠形式的新型风叶,并对叶片进行气动性能分析、噪声分析及最终试验验证。具体为选取叶片的若干径向弯掠截面作为优化位置,采用CFD气动优化方法对各径向弯掠截面角度进行调整,得到最优径向弯掠角优化风叶,并进行噪声分析和试验验证。
1 轴流风叶流场模型
1.1 建立流场仿真模型
空调室外机整体结构如图1所示,散热风道主要部件为轴流风叶、前面板、蒸发器、中隔板、电机支架等。本文主要研究对象为轴流风叶优化,对于室外机风道结构,前面板的导风圈对风叶性能影响较大,因此为提高计算效率,建立如图2所示包含导风圈的风叶流场模型。模型主要由进风域、出风域及旋转域组成,风叶位于旋转域内,外围采用导风圈结构,进风域和出风域通过旋转域连接。综合计算效率和精度,将进风域长度设计为风叶直径的2倍,出风域长度为风叶直径的5倍。风叶直径为340 mm,叶高为125 mm。
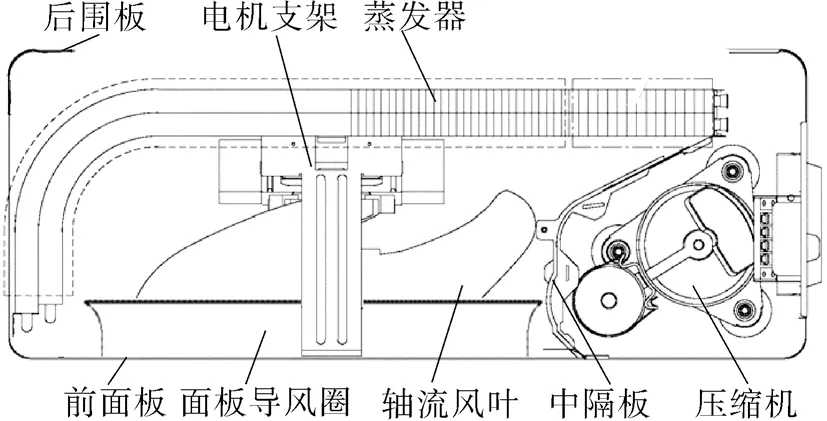
图1 空调室外机主要结构Fig.1 Main structure diagram of outdoor unit of air conditioner

图2 风叶流场模型示意Fig.2 Schematic diagram of fan blade flow field model
运用CFD进行流场仿真分析,研究叶片不同径向弯掠角的气动性能。采用Segregated隐式算法,运用多参考系坐标模型(MRF)定义旋转域,SIMPLE压力-速度耦合算法,湍流模型选择修正k-ε模型(RNG k-ε),壁面条件为多尺度壁面函数法,湍流动能、湍流耗散项、动量方程均采用二阶迎风格式。零静压进、出口(pressure-inlet和pressure-outlet)边界条件。
1.2 网格无关性验证
对初始风叶模型使用四面体网格进行划分,并对旋转域进行加密,在同条件下监控出口体积流量,并选定叶片压力面尾缘局部区域作为静压监控,如图3所示,设定风叶转速为800 r/min。图4示出不同网格划分方式下出口流量和监控静压曲线,表1以Case4为基准将Case1~3流量与之作差,静压同样基于Case4按比值处理,结果表明随着网格密度由Case1增加到Case3时,出口流量和监控区域静压随之增大,说明合理的网格密度和质量对控制计算精度十分重要。当进一步加大网格密度到Case4后,出口流量和监控区域静压基本保持不变,说明此时计算结果已趋于稳定,与网格密度关联性不大。考虑计算效率,后续优化模型的网格种子布置将采用Case3规格进行网格划分。
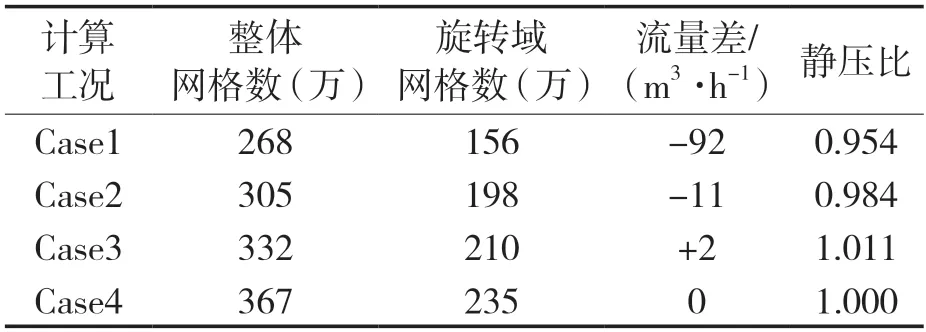
表1 网格无关性验证结果Tab.1 Grid independence verification results

图3 风叶网格及静压监控区Fig.3 Fan grid and static pressure monitoring area

图4 不同网格数量结果对比Fig.4 Comparison of results at different grid numbers
1.3 初始风叶内流场分析
从叶片表面压力和流道内涡量两个维度对初始风叶模型进行内流场分析。从叶片压力面静压(见图5)可知,由叶片外缘向轮毂方向看,叶片外缘由于旋转速度最大,压力相对叶片内部更大,由外缘的最大值49 Pa逐渐减小到轮毂附近的5 Pa。从叶片前缘至尾缘方向看,压力逐渐增加,且在靠近导风圈位置变化最明显,由前缘的10 Pa增加到导风圈附近的49 Pa,说明叶片外缘尤其是靠近尾缘的后半段为主要做功区域,受导风圈影响,在其附近气流压力最大,此处叶片做功能力最强。
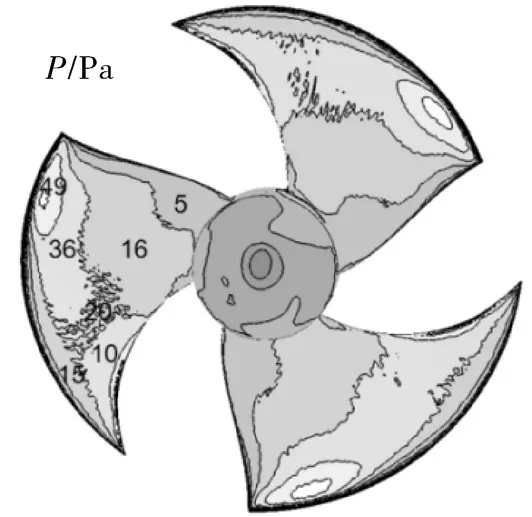
图5 初始风叶压力面静压Fig.5 Static pressure diagram of initial fan blade pressure surface
根据叶片周边涡量(见图6)可知,在叶片外缘后半区存在大量的泄漏涡,涡形以螺旋发散为主,并延伸至下一叶片从而直接冲击表面。同样可看到在叶片表面包裹着涡流,这是因为受边界层作用,气流经过叶片表面时产生了细微涡流,但相比泄漏涡,叶片表面涡流较小,对风叶气动性能影响有限。

图6 初始风叶涡量Fig.6 Figure of initial fan blade vorticity
由噪声原理可知,涡是产生气动噪声的主要原因,因此叶片外缘即最大做功区域是造成风叶噪声的主要位置,如何抑制或减小叶片外缘泄漏涡是风机降噪的重点研究内容。基于上述初始风叶内流场特征,通过调整叶片径向弯掠角,在确保叶片做功能力的同时降低外缘泄漏涡,实现以最合理的叶片弯掠角达到增风降噪目的。
2 叶片径向弯掠角优化
2.1 径向弯掠角定义
为研究风叶外缘不同径向弯掠角对风机气动性能的影响,将初始风叶沿径向等分为4部分,由轮毂往外缘依次将截线分为1#~4#,沿周向均分成3部分,其截线分别为a~d,如图7所示,自定义叶片径向弯掠角为沿叶片径向切线与水平方向夹角α,如图8所示。

图7 风叶区域划分示意Fig.7 Schematic diagram of fan blade area division

图8 叶片径向弯掠角定义Fig.8 Definition of fan blade radial sweep angle
由于主要研究叶片外缘泄漏涡,因此将以圆周c线为起始线进行径向弯掠角的调节,比如1#截线径向弯掠角为该截线与c线交点的切线,与过该交点的水平面夹角,命名为α1,其它截线的径向弯掠角定义以此类推分别为α2,α3,α4。采用控制变量法对不同径向弯掠角流场进行气动仿真计算。
2.2 不同径向弯掠角全压效率结果
通风机全压效率计算公式如下,其综合考虑风叶流量、压力、轴功率等关键气动性能,可较全面评估风叶性能,因此将全压效率作为轴流风叶优化评价指标较为合理。
φ=(PQ)/W
式中,φ为全压效率;P为风叶全压;Q为风叶流量;W为风机轴功率。
根据叶片径向弯掠角定义方式,以初始风叶角作为0°,将α1,α2,α3,α44个弯掠角通过控制单一变量法分别按表2进行独立旋转,如当α1旋转1个角度时,其他弯掠角保持0°初始状态,向压力面旋转为“+”,反之为“-”。当某个径向弯掠角完成旋转后,采用二次曲面修正模型并进行流场计算,得到其全压效率。

表2 弯掠角旋转角度Tab.2 Angle of rotation of sweep angle (°)
图9示出4个径向弯掠角经二次拟合的全压效率曲线,可知各旋转角度对风机效率均有不同程度的影响。整体观察4根曲线,从α1到α4曲线峰值逐渐增大,曲线平缓度也逐渐降低,说明叶片外缘不同位置的径向弯掠角对全压效率的影响具有最合理范围。提取每根曲线对应的峰值点并统计,见表3,得到各径向弯掠角独立变化后的最优效率参数。从表格峰值看出α1和α2提升量较小,无明显变化,而随着弯掠角往尾缘延伸,至α4时其效率提升了3.15%,效果显著提升,因此从叶片前缘至尾缘,径向弯掠角的调整对全压效率的改善作用逐步增加,即叶片做功能力越强区域,对全压效率的影响越明显。
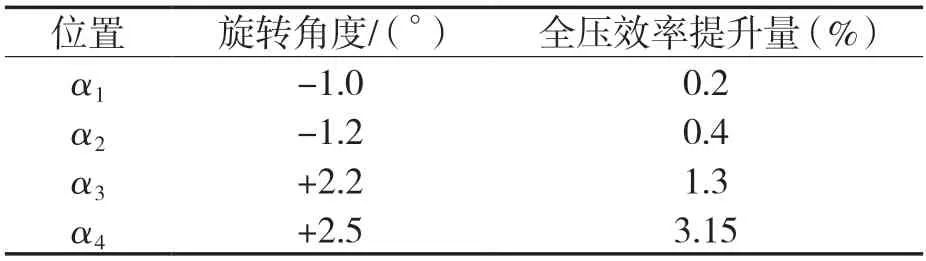
表3 不同径向弯掠角的全压效率提升值Tab.3 Total pressure efficiency improvement values at different radial sweep angles
2.3 优化风叶内流场分析
采用表3所示的各弯掠角最佳旋转角度重新设计风叶模型,形成最终优化风叶,并进行流场仿真。将计算结果与初始风叶进行比较,如表4所示,优化风叶风量增加58 m3/h,全压基本持平,但轴功率降低了1.3 W,综合而言全压效率由初始风叶的73.1%提升到76.7%,提升3.6%,改善效果显著。
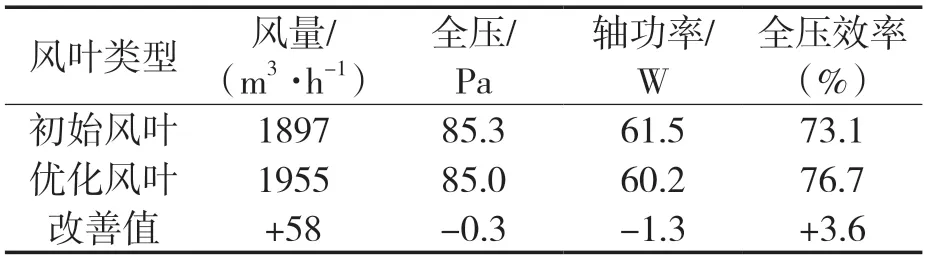
表4 风叶全压效率Tab.4 Total pressure efficiency of fan blade
图10示出优化风叶表面静压分布,与1.3节的初始风叶计算结果进行比较,可看出优化风叶静压峰值由原来的49 Pa增加到53 Pa,叶片外缘整体压力明显增大,其他相同区域压力也得到提升,压力梯度分布更为均匀,说明优化风叶做功能力增强,叶片表面气流流动更流畅。

图10 优化风叶压力面静压Fig.10 Static pressure diagram of optimized fan blade pressure surface
同时结合图11的涡量进行分析,可知靠近叶片尾缘(尤其叶片进入导风圈区域)周围涡量仍存在明显泄漏涡,但相比初始风叶减少很多,泄漏涡得到明显改善,而泄漏涡的有效抑制促进了风叶有效做功能力,这也是全压效率得以提升的主要原因,此外也会对噪声产生有利的影响。

图11 优化风叶涡量Fig.11 Vorticity diagram of optimized fan blade
2.4 优化风叶气动噪声仿真分析
对于单级旋转风叶,通过风叶与气流的冲击作用进行做功,其噪声源主要为偶极子,因此本文首先运用非稳态LES大涡模拟湍流模型得到稳定的风叶流场,然后采用FW-H声比拟方法对优化叶片和初始叶片进行气动噪声仿真,并设置风叶为噪声源,距离风叶正前1m处设为噪声接收点。流场和噪声计算时间步均为0.000 1 s,风叶转速仍为800 r/min,总计算时长为1 s,得到5 000 Hz的频谱。
图12示出优化风叶和初始风叶声压级频谱曲线,从曲线中可看出,不同频段的两种风叶噪声趋势基本相同,在500Hz内优化风叶噪声值与初始风叶相当,这是因为在低频率时主要以旋转噪声为主,对于同为旋转风叶而言二者相差不明显,而在500Hz以上时,优化风叶噪声幅值低于初始风叶,说明以气动噪声为主的高频段,优化风叶具有较好的降噪效果。
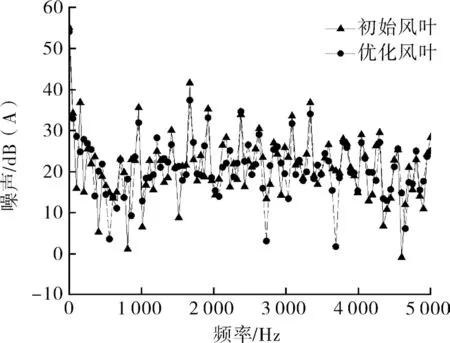
图12 风叶声压级频谱曲线Fig.12 Spectrum curve of sound pressure level of fan blade
同时根据接收点噪声结果,优化风叶噪声值为56.6 dB(A),初始风叶为57.7 dB(A),噪声降低1.1 dB(A),进一步表明优化风叶具有较好的噪声表现。如前所述轴流风叶的叶片外缘做功能力强,气流对叶片的冲击大,且外缘的泄漏涡较为集中,从而冲击噪声和涡流噪声均较大,因此通过改善叶片外缘径向弯掠角,减小泄漏涡对降低风机整体气动噪声有积极效果。
3 风机性能试验验证
3.1 试验与仿真数据对比
将优化风叶和初始风叶分别制作精密手板,并安装于同一台空调室外机,在风量试验台和半消音噪声室进行同条件下两风叶的风量、功率、噪声性能测试。其中噪声测试时室外机放置在台面上,底部垫0.5 cm厚橡胶垫以排除振动噪声影响,室外机风道中心距地面1.0 m,噪声探头据地面1.0 m,正对风道中心点1.0 m,如图13所示。

图13 噪声测试台Fig.13 Noise test bench
通过调节风叶电机输入电压控制风叶转速,风叶在转速为800 r/min时仿真与试验的风机性能参数对比见表5。
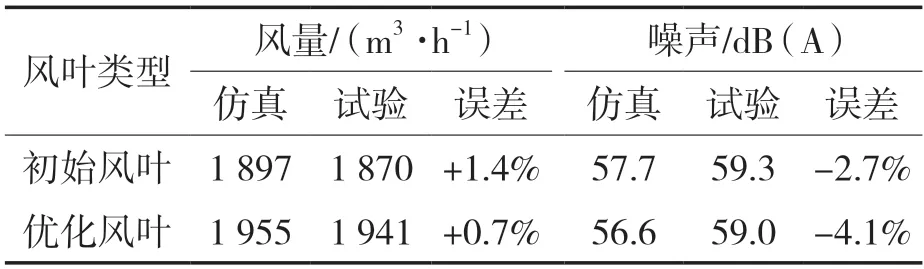
表5 风叶性能仿真与试验对比Tab.5 Comparison between simulation and experiment of fan blade
从表中看出,风量仿真值基本与测试值持平,而噪声误差较大,优化风叶噪声误差达到4.1%,这是因为噪声仿真仅考虑偶极子作用,而忽略了实际产品中振动噪声、气动四极子及其他结构作用产生的噪声,因此实际噪声值会高于仿真值,但从趋势上看还是相吻合,以此可验证前面仿真数据的可靠性。
3.2 风机性能试验数据分析
不同转速下初始风叶和优化风叶性能试验测试曲线如图14所示。从风量-功率曲线可知,优化风叶同风量时比初始风叶功率低1.9~3.1 W,从风量-噪声曲线可看出优化风叶同风量噪声低1.0~2.1 dB(A)。以1 800 m3/h为基准对比同风量下的功率和噪声差异,风叶功率由初始的56.0 W降低至53.5 W,相比初始风叶效率提升约4.5%,噪声降低1.8 dB(A),实际改善效果明显,且试验测试数据与仿真结果趋势基本相同,说明本文研究方法对轴流风叶弯掠形式优化具有可靠指导意义。
4 结论
(1)通过仿真优化叶片径向弯掠角,重构的优化风叶表面压力分布更为合理,高效做功区加大,整体全压效率提升3.6%,叶片外缘泄漏涡得到有效抑制。
(2)采用FWH模型对风叶进行噪声仿真,结果表明优化风叶降噪1.1 dB(A),频谱曲线上大部分频率噪声更低,具有较好的噪声优势。
(3)试验结果表明优化风叶同风量比初始风叶功率低1.9~3.1 W,噪声低1.0~2.1 dB(A),1 800 m3/h的基准风量下优化风叶效率提升约4.5%,噪声降低1.8 dB(A),趋势与仿真结果基本相同。
