空调室外机叶轮振动与噪声关联特性试验研究
2023-10-31代元军何振雄李保华
代元军,何振雄,李保华,吴 柯
(1.新疆农业大学 机电工程学院,乌鲁木齐 830052;2.上海电机学院 机械学院,上海 201306;3.新疆工程学院 能源工程学院,乌鲁木齐 830091)
0 引言
随着人们生活品质的不断提升,在关注空调室内机的振动与噪声的同时,也对室外机的振动与噪声关注日益增加。作为室外机主要部件之一的叶轮,其运行过程中产生的结构振动经传导至室内壁面,会造成异常的低频噪声、同时也会降低叶轮运行的可靠性和高效性。且叶轮运行过程中的气动噪声也会造成严重的噪声污染,进而影响消费者的体验感,因此,空调室外机叶轮的振动、噪声是一个亟待解决的热点性研究问题[1-4]。
关于空调室外机叶轮的噪声研究,王梦豪等[5]采用数值模拟的方法研究了4种仿鹄翼型对叶轮降噪效果。马列等[6]采用数值模拟研究了尾缘结构缺陷对叶轮噪声特性的影响。周伟峰等[7]发现出风格栅可以减小叶轮的气流旋转动能损失并提高其静压效率,从而降低叶轮的气动噪声。王梦豪等[8]把计算流体力学和声类比相结合对叶轮进行了声场研究。陈亚伟[9]研究了外缘翻边叶轮的气动性能,发现外缘翻边可以降低叶轮的噪声。李明等[10]利用有限元分析进行了高速叶轮的气动噪声仿真模拟。马丽华等[11]利用有限元分析模拟了叶轮远场接收点位置的噪声特性和气动噪声源的分布。马海林等[12]利用湍动能噪声模型仿真了风机叶轮噪声。仲惟燕等[13]利用数值模拟仿真了叶轮在设计工况下的气动噪声源和流场的分布。孙迎浩等[14]采用CFD数值模拟与试验相结合研究了不同前缘型状对叶轮的噪声影响。LIM等[15]对后缘具有小翼的叶轮进行噪声特性试验和数值分析。PARK等[16]采用CFD软件对叶轮的流场进行了模拟。IWASE等[17]采用大涡模拟计算了叶轮的气动噪声。通过上述文献分析可知:空调室外机叶轮噪声研究主要集中在叶轮优化设计,如文献中提到的仿鹄翼型、尾缘结构缺陷等与叶轮噪声形成的机理分析。
目前,研究人员对空调室外机叶轮噪声的研究较重视,但都是单独开展噪声的研究,并未涉及叶轮振动特性研究及振动与噪声耦合特性的关联性研究。为了降低空调室外机叶轮的振动和噪声,本文提出了一种空调室外机叶轮尾缘锯齿结构设计方案,并以此开展叶轮振动特性研究及振动与噪声耦合特性的关联性研究,为空调室外机叶轮的减振与降噪提供借鉴。
1 试验方案设计
1.1 叶轮的模态测试方案设计
1.1.1 被测对象
本次测试以某型号空调室外机叶轮为被测对象,叶轮直径D为400 mm,轮毂直径d为100 mm,额定转速700 r/min,叶片数为3,如图1所示。
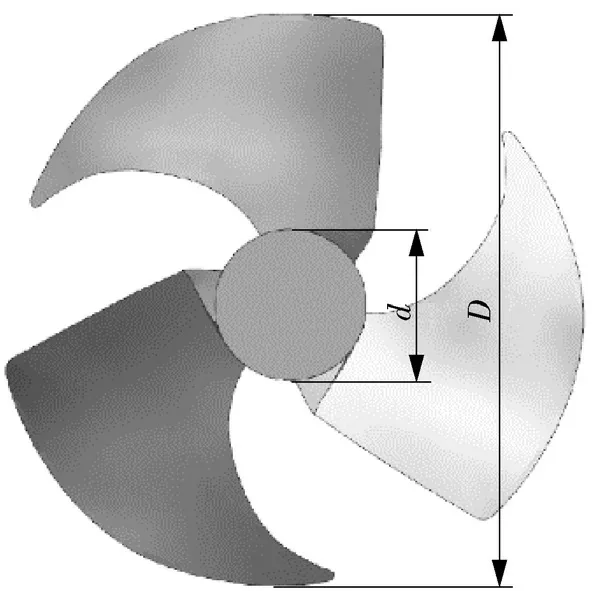
图1 空调室外机叶轮Fig.1 Outdoor unit impeller of the air conditioner
为了探究尾缘锯齿结构对叶轮的振动与噪声特性的影响,设计了一种改型叶轮,如图2所示。其锯齿参数见表1。对尾缘进行开槽,槽为三角形,其锯齿齿角θ,锯齿齿高h,锯齿齿距d。

表1 尾缘锯齿参数Tab.1 Parameters of serrated impeller at the trailing edge
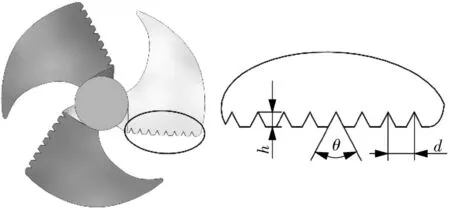
图2 尾缘锯齿叶轮Fig.2 Serrated impeller at the trailing edge
1.1.2 测试系统、试验原理与试验设备
测试系统为B&K振动分析系统,试验原理为频谱分析法。采用瞬态激励方法,测试叶轮用固定件进行安装固定,叶轮在力锤激励下,其振动信息由传感器采集,再输送给数据采集前端,最后经网线输送给振动分析单元。试验设备如下:8206-002型敲击力锤,灵敏度为2.183 mV/N;4507-B-004型加速度传感器,灵敏度为9.941 mV/(m·s-2);LAN机箱;12通道数据采集前端。
1.1.3 测点布置
按等分的原则选择了15个测点,测点布置如图3所示,1~15号点为加速度传感器布置点,16~21号点为激励点,频率范围为0~300 Hz,激励点的敲击次数为5次。
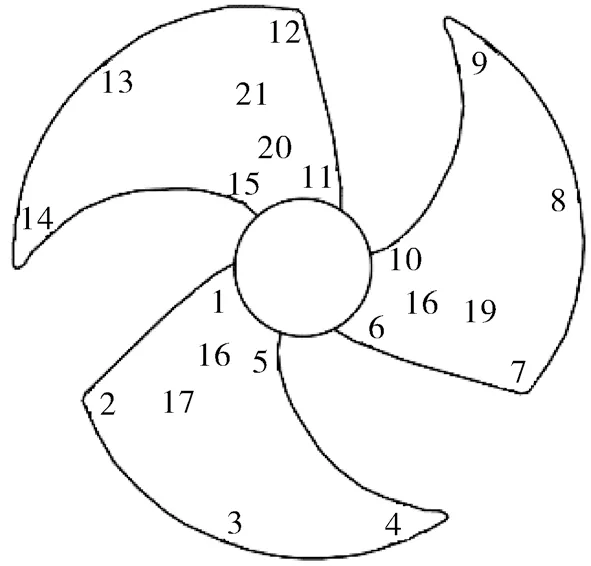
图3 激励点及测点分布Fig.3 Distribution of excitation points and measurement points
1.2 叶轮动频特性试验方案设计
1.2.1 被测对象、测试系统、试验原理及试验设备
被测对象同模态试验一致,测试系统采用B&K振动分析系统,试验原理使用频谱分析法。试验设备如下:4524-B型传感器,灵敏度为9.853 mV/(m·s-2);2981型激光转速探头,其转速范围为0~300 000转;电容电机专用变频器,其频率调控范围为0~50 Hz。
1.2.2 测点分布
在空调室外机的电动机的前端和后端安装三向振动加速度传感器,在叶轮的叶尖位置布置反光条,在距离叶尖一定距离处布置激光转速探头,叶轮动频特性测点如图4所示。
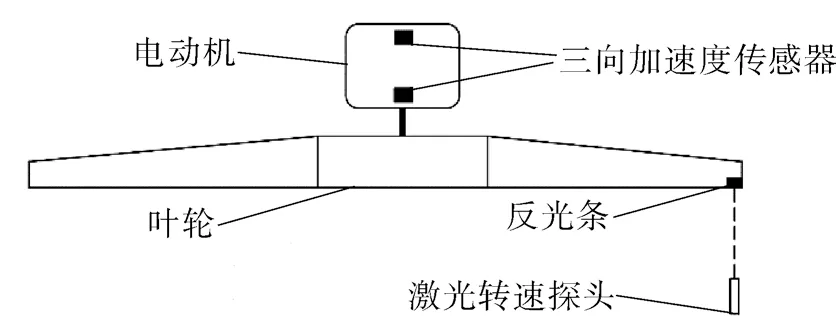
图4 叶轮动频特性测点Fig.4 Schematic diagram of measurement points for dynamic frequency characteristics of impeller
1.3 叶轮振动与噪声耦合特性的测试方案设计
1.3.1 被测对象、测试系统、测试原理与测试设备
被测对象和模态试验一致,测试系统为B&K振动噪声测试系统,测试原理为频谱分析法。振动噪声时频数据使用2只振动传感器、4只噪声传感器采集,采用频谱分析法处理分析数据。试验设备如下:声传感器使用BSWA公司的MPA 201型传感器,其灵敏度为48.4 mV/Pa,其他设备和动频特性试验设备一致。
1.3.2 测点布置
振动与噪声耦合测试的三向振动加速传感器安装和叶轮的动频试验安装一致,噪声测点如图5所示,在叶轮叶尖处布置4个声音传感器。以叶轮的旋转轴线和旋转平面的交点为原点O,轴向远离叶轮旋转平面的方向为X轴正方向,以垂直于X轴向右为Y轴正方向,测点系统距叶轮旋转平面10 cm,测点2对准叶轮叶尖,相邻2个测点的间距为3 cm。
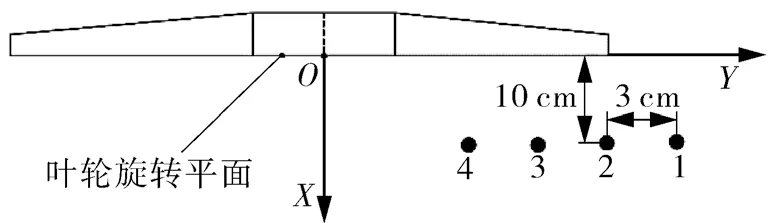
图5 振动噪声测点布置Fig.5 Layout diagram of vibration and noise measurement points
2 测试结果与分析
2.1 叶轮的模态数据分析
分析试验数据得到叶轮的固有频率和阻尼比如图6所示,物体的固有频率、阻尼比越大,其结构稳定性就越强[18-20]。由图分析可知:随着叶轮阻尼比的下降,叶轮的固有频率呈现出上升态势。随着模态阶数的上升,固有频率呈现增大趋势,且尾缘锯齿叶轮的固有频率总是高于未改型叶轮,其中1~5阶固有频率分别提高3.45%,11.18%,8.32%,20.35%,17.16%;随着模态阶数的上升,阻尼比整体呈现减小趋势,从整体上来看,尾缘锯齿结构叶轮阻尼比有所提高,其中2~5阶阻尼比分别提高10.02%,13.31%,30.46%,2.97%。
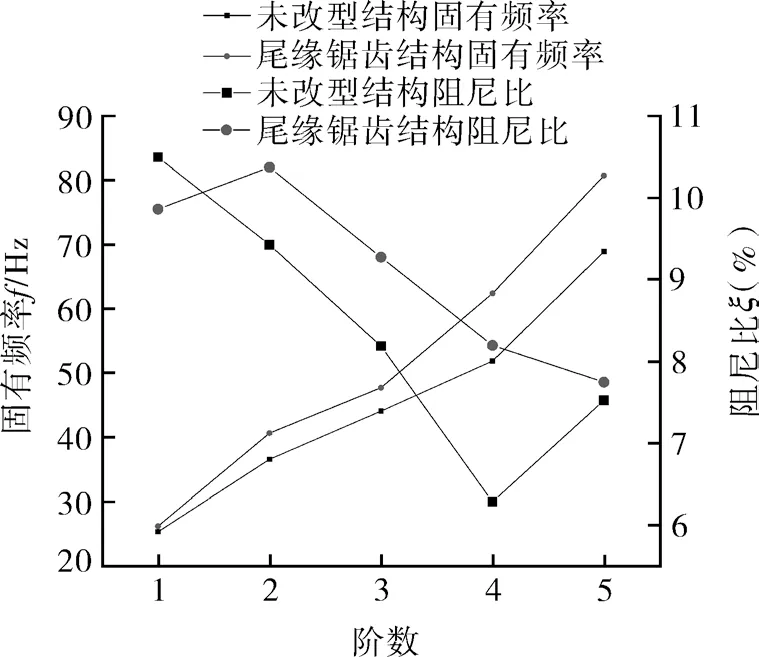
图6 叶轮各阶固有频率、阻尼比Fig.6 The natural frequency and damping ratio of each order of the impeller
尾缘锯齿叶轮固有频率和叶轮阻尼比提高原因是由于尾缘锯齿结构所特有的三角锯齿结构决定其较强的稳定性与刚度特性,且尾缘锯齿结构与未改型叶轮相比,叶轮尾缘质量减小,因此尾缘锯齿结构可以增大叶轮的模态参数。叶轮的激振频率与固有频率相等或者接近时,叶轮则会产生共振,尾缘锯齿结构能提高其固有频率,降低叶轮共振概率,增加叶轮结构的稳定性,为空调室外机叶轮的减振提供一种新的方法。
2.2 叶轮动频特性数据分析
叶轮转速n和动态频率f的曲线关系称为动频曲线图,判断叶轮是否共振的工程图解法。利用这种曲线关系图可以找出叶轮共振时的自振频率与激振频率。主要根据共振点是否位于叶轮主要运行区来判断叶轮结构的动态性能好坏。对于三叶片空调室外机叶轮,基频的3倍频为主振频率,并将主振频率3P的±10%上下区间定义为共振区。动态频率曲线与共振区会相交,且相交两点,这两交点的频率差值为频宽,且动态频率曲线和3P主射线相交的点,即为共振转速。频宽越大,共振转速越靠近额定转速,则共振机率越大,反之越小。本文以共振裕度解释这一现象,共振裕度越大,叶轮共振概率越低,且共振裕度可以表示为:
如图7示出了叶轮的动频曲线,叶轮的振动频率随着转速的增大而增大,从图中可以看出尾缘锯齿结构可以调整叶轮振动频率曲线的走势,并由软件计算得出叶轮的频宽、共振点转速、共振裕度。根据数据分析可知:未改型叶轮共振频宽为1.64 Hz,共振点对应的转速为609.47 r/min,共振裕度为12.93 %。尾缘锯齿结构叶轮共振频宽为0.90 Hz,共振点对应的转速为585.71 r/min,共振裕度为16.33%。通过和未改型叶轮对比分析,可知尾缘锯齿结构叶轮的动频曲线经过共振区的频宽较窄,共振裕度更高,因此尾缘锯齿结构能使空调室外机叶轮更快的脱离共振区,降低共振概率。其原因为在叶轮旋转机械中,叶片的稳定性关乎其能否正常运行,载荷及其振动变形量决定叶轮叶片的稳定性。其中离心力载荷、叶片质量引起的重力载荷、流体对叶片产生的气动力载荷是作用在叶轮叶片的三大载荷,尾缘锯齿结构造成的尾缘质量减少以及降低流体对叶片尾缘产生的气动力载荷,这在一定程度上减小了这三者数值的大小,进而可以减小叶轮振动频率,提高叶轮稳定性。
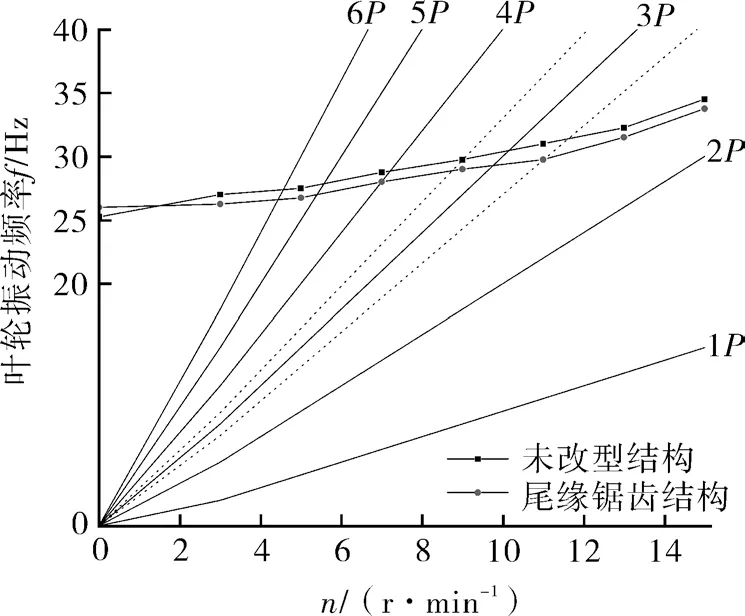
图7 叶轮一阶坎贝尔图Fig.7 First-order Campbell diagram of the impeller
2.3 叶轮振动与噪声耦合特性分析
2.3.1 叶轮近尾迹噪声变化规律
图8示出了叶轮额定转速为700 r/min时,在距离叶尖10 cm处各测点所对应的声压级关系。分析发现:随着测点位置从1号到4号推移,相应位置的声压级先增大后减小,在1号测点处未改型叶轮的声压级为84.26 dB,改型叶轮的声压级为80.89 dB,声压级下降4.00 %。在2号测点处未改型叶轮的声压级为88.43 dB,改型叶轮的声压级为85.11 dB,声压级降低3.75 %。在3号测点处未改型叶轮的声压级为86.82 dB,改型叶轮的声压级为83.43 dB,声压级下降3.90 %。在4号测点处未改型叶轮的声压级为83.56 dB,改型叶轮的声压级为80.24 dB,声压级降低3.97 %。由数据分析可知,叶轮在叶尖处的噪声值最大,且尾缘锯齿结构叶轮具有良好的降噪效果。
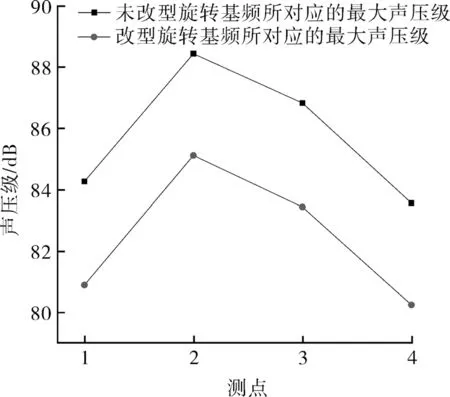
图8 转速为700 r/min,X=10 cm处各测点所对应的声压级Fig.8 The speed is 700 r/min,and the sound pressure level corresponding to each measurement point at X=10 cm
其原因是尾缘锯齿结构可以造成叶轮尾缘位置产生旋涡流动现象,减小相干性,且不同尾缘高度噪声相位不一样,从而使噪声叠加起来的声压级有所下降,同时也可以使尾缘大涡分解为小涡,促使马蹄涡的产生,造成尾迹混合,推迟边界层分离,以上变化造成了尾缘锯齿结构具有良好的降噪特性。
2.3.2 离心力载荷对空调室机叶轮振动噪声耦合特性分析
调节单项电容电机专用变频器使空调室外机电机的转数分别为300,420,540,660 r/min。单独分析离心力载荷规律增大时,空调室外机未改型与改型叶轮的振动和噪声的耦合特性。
以2号测点(叶尖位置)为例,图9示出叶轮振动特性与旋转基频噪声耦合关系,揭示了空调室外机未改型与改型叶轮在离心力载荷增大的情况下的1阶振动频率、2阶振动频率与叶轮的旋转基频、叶尖位置所对应声压级耦合关系。由图9可知,未改型叶轮的1阶振动频率分别为28,29,29.75,31.5 Hz,改型叶轮的1阶振动频率分别为26.75,28,28.75,29.75 Hz,与未改型叶轮相比,1阶振动频率分别下降4.46%,3.45%,3.36%,5.56%。未改型叶轮的2阶振动频率分别为43,43.5,45.75,46.75 Hz,改型叶轮的2阶振动频率分别为42.25,42.75,45.25,46 Hz,与未改型叶轮相比,2阶振动频率分别下降1.74%,1.72%,1.09%,1.60%。综上分析可知:叶轮1阶、2阶振动频率随着转速的增大而增加。因为叶轮转速越大,所产生的离心力也越大,从而导致叶轮的形变加大,最终致使振动频率的提高。由于改型后的叶轮尾缘质量减少,其离心力和气动力相对于未改型叶轮是衰减状态,从而导致振动频率降低。当叶轮旋转基频为15,21,27,33 Hz,未改型叶轮旋转基频的声压级分别为58.25,62.36,66.37,70.77 dB,改型叶轮旋转基频的声压级分别为55.12,59.15,63.06,67.16 dB,与未改型叶轮相比,改型叶轮旋转基频的声压级分别下降5.37 %,5.15%,4.99%,5.10%;未改型叶轮叶尖位置的声压级分别为75.56,79.45,83.12,87.13 dB,改型叶轮叶尖位置的声压级分别为72.16,76.04,79.88,83.57 dB,与未改型叶轮相比,改型叶轮叶尖位置的声压级分别下降4.50 %,4.29%,3.90%,4.09%。由声压级分析可知:叶轮旋转基频的声压级、叶尖位置的声压级随着转速的增大而增加,且尾缘锯齿结构叶轮的声压级值总是低于未改型叶轮的声压级值,因此尾缘锯齿结构叶轮具有良好的降噪性能。
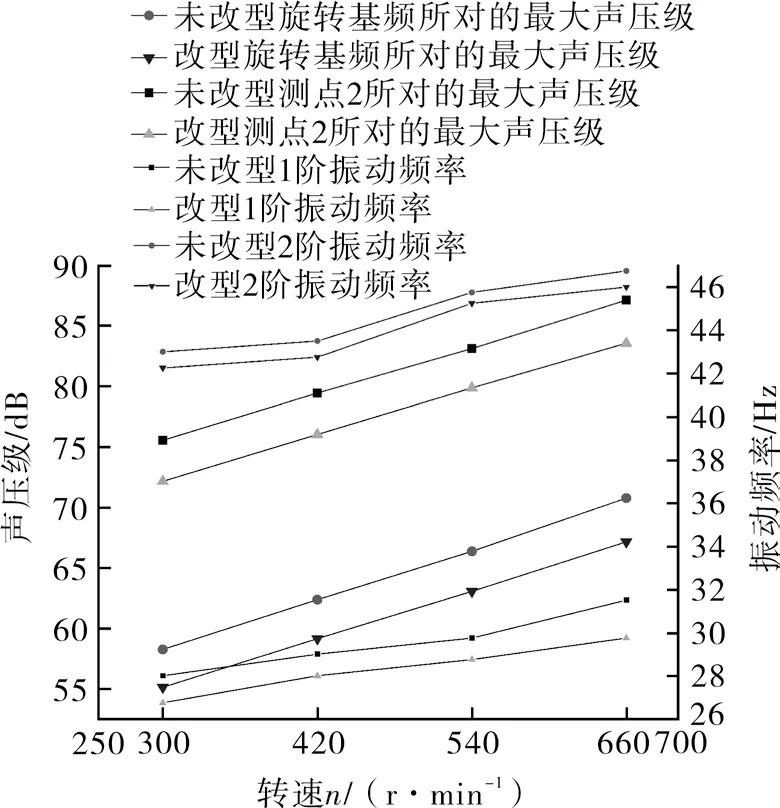
图9 不同转速下叶轮振动频率与旋转基频噪声、测点2噪声耦合关系Fig.9 Coupling relationship diagram between impeller vibration frequency and rotational fundamental frequency noise and noise of measurement point 2 at different speeds
随着叶轮离心力载荷增大,分析叶轮前两阶振动频率与其旋转基频、叶尖位置的声压级耦合关系,研究结果表明:随着离心力载荷的增大,叶轮的前2阶振动频率,各旋转基频、叶尖位置的声压级也随之增大,因此叶轮振动频率和声压级具有一定程度上的正相关性。
3 结论
(1)通过叶轮的固有频率与阻尼比分析可知,尾缘锯齿结构可以改良叶轮的模态参数,优化了其静态振动特性。
(2)通过叶轮的坎贝尔图分析可知,尾缘锯齿结构可以调整叶轮振动频率曲线走势,减小频宽、共振转速,增大共振裕度,改善了其动频振动特性。
(3)当转速分别为300,420,540,660 r/min时,未改型叶轮1阶振动频率分别为28,29,29.75,31.5 Hz,2阶振动频率分别为43,43.5,45.75,46.75 Hz;其叶尖位置声压级分别为75.56,79.45,83.12,87.13 dB,旋转基频声压级分别为58.25,62.36,66.37,70.77 dB。未改型叶轮前2阶振动频率与其旋转基频、叶尖位置的声压级随着离心力载荷的增大而增大,且其振动频率与声压级呈现正相关关系。此外改型叶轮也具有上述相同规律。
