基于自适应α-β滤波算法的机动目标跟踪方法
2023-10-31尹邦政李冠贤单梓琪
尹邦政,朱 静,李冠贤,单梓琪,魏 童
(1 广州铁路职业技术学院 广东 广州 510430) (2 广州大学 广东 广州 510006)
0 引言
机动目标跟踪技术早已成为了科学家们重点研究的热门课题之一[1]。随着现代科学和技术的进一步发展[2],出现了不少有效的机动目标跟踪算法,但因其复杂度与计算量导致难以应用在实际工程中[3]。如何在实际工程中较好的跟踪目标,一直是机动目标跟踪技术研究领域中备受重视和关注的科学技术问题之一,这不仅在学术上具有十分重要的理论意义[4],还有广泛的科学技术应用和研究前景。目标跟踪算法的核心问题是滤波,而滤波是为了预估当前运动目标的运动状态。为了跟踪不同的运动目标,人们提出了大量的滤波方法,这些方法有α-β滤波和α-β-λ滤波、最小二乘滤波、线性自回归滤波、维纳滤波、两点外推滤波、卡尔曼滤波和扩展卡尔曼滤波等[5]。而α-β系列滤波算法作为实际工程中应用最多的滤波器,它可以不依赖系统的具体模型及误差噪声分布的限制,并且通过较少的计算量便可获得较为准确的物体运动轨迹。但是该算法的不足主要体现在跟踪较为复杂的运动时,会产生较大的误差。
本文致力于寻找一种新的机动目标跟踪方法,用于上述机动目标跟踪效果不佳的场景,为此提出了“自适应滤波”方法。通过应用数值优化方法将自适应滤波设计问题变成数值优化问题。自适应α-β滤波方法是基于α-β滤波算法与α-β-λ滤波算法设计的,它的特点是以无偏估计原理和最小方差原理,设定2种不同的运动状态,以α-β滤波算法与α-β-λ滤波算法为基础,通过自适应参数实现2种状态的自由切换,获得一个更加准确的目标位置。
1 自适应滤波算法原理
1.1 机动目标跟踪模型
机动目标运动状态是一种随机过程,跟踪机动目标需要分析目标运动的特征并预测目标的运动轨迹。因此,需要建立一种数学模型来准确描述机动目标的运动状态变化,该数学模型能匹配目标真实运动状态,匹配程度越高跟踪精度越好。但是由于目标运动是频繁的、复杂多变的状态变化,大体可以分为机动和非机动,而要建立能满足两者的模型是比较困难的,如目标突然加速或者转弯,从非机动状态转变为机动状态。如果目标只是做简单的没有太大状态变化的非机动时,这种目标模型的建立就相对比较简单,且能真实地反映目标运动状态。但是在很多场合下,通过雷达等传感器所传来的数据是比较复杂且含有大量的噪声,会导致不能事先获得目标的先验知识,这种情况下只能采用估计理论知识来近似地描述。因此,目标模型地建立首先要考虑目标运动模型的不确定性和非线性,纵观现有的模型中,最为经典的跟踪模型有匀速(constant velocity,CV)模型、匀加速(constant acceleration,CA)模型和多个模型之间切换的交互式多模型等。
跟踪目标的运动状态通常分为机动状态和非机动状态2种。当跟踪目标在运动过程中出现机动与非机动状态来回切换的情况时,很难建立一个同时能够满足这2种运动条件的模型,这时就需要建立不同的数学模型来分别对应跟踪目标的机动和非机动状态。此处定义跟踪目标的非机动运动为匀速直线运动,采用CV模型匹配跟踪目标的运动状态;定义机动运动为匀加速直线运动,采用CA模型匹配跟踪目标的运动状态。
1.1.1 CV模型
CV模型被认为跟踪物体在做匀速运动时的运动模型,因为物体是在做匀速运动的,而α-β滤波器可以较为精确的跟踪匀速目标,可以通过α-β滤波器来获取目标的实时位置。经典α-β滤波器可表示为式(1)、式(2)、式(3)、式(4):
x(k|k-1)=x(k-1)+tv(k-1)
(1)
v(k|k-1)=v(k-1)
(2)
x(k)=x(k|k-1)+α[xl(k)-x(k|k-1)]
(3)
v(k)=v(k|k-1)+β[xl(k)-x(k|k-1)]/t
(4)
式(1)、式(2)、式(3)、式(4)中:x(k|k-1)为k时刻的位置预测值;v(k|k-1)为在k时刻速度的预测值;x(k)为经过α-β滤波器后k时刻的位置;v(k)为经过α-β滤波器k时刻的速度;xl(k)为每次雷达或其他测量系统在k时刻返回的数据。因为在模型中认为没有加速度,故k时刻的速度预测值就是经过α-β滤波器k-1时刻的速度。
1.1.2 CA模型
当物体开始做变速运动时,α-β滤波器已经无法较好地跟踪目标,此时通过经典α-β-λ滤波器来对目标进行跟踪,这便是CA模型。α-β滤波器只能对匀速运动的目标进行跟踪,而α-β-λ滤波器则是针对匀加速的目标进行跟踪的滤波算法。α-β-λ滤波器是在α-β滤波器的基础上增加了系统的维数,将目标的加速度作为一项参数加入到系统的状态向量中,此时的目标状态向量是三维的向量,即包含目标的位置x、速度v、加速度a这3个状态分量。
经典α-β-λ滤波器可表示为式(5)、式(6)、式(7)、式(8)、式(9)、式(10):
(5)
v(k|k-1)=v(k-1)+t·a(k-1)
(6)
a(k|k-1)=a(k-1)
(7)
x(k)=x(k|k-1)+α[xl(k)-x(k|k-1)]
(8)
v(k)=v(k|k-1)+β[xl(k)-x(k|k-1)]/t
(9)
a(k)=a(k|k-1)+2γ[xl(k)-x(k|k-1)]/t2
(10)
经典α-β-λ滤波器与α-β滤波器基本变量一致,但在CA模型中有加速度参与到运动之中,因此在α-β滤波器的基础上增加了式(7)与式(10)。
1.2 变维卡尔曼滤波算法
当运动目标做非机动运动时,基本的滤波与预测方法就可以很好地跟踪目标,但做机动运动时,其运动特征时刻在发生变化,如加速度、速度、运动方向等都会在不断地变化,当其运动状态发生改变时,由于持续的变化所带来的滤波误差有可能比较大,而具有机动检测能力的变维卡尔曼滤波(variable dimension,VD)算法非常适合处理该类误差。一旦确定目标的运动模型,就开始对运动目标进行跟踪,并不断地检测目标的状态,当检测到目标的状态发生变化时,采用VD算法来实现CV模型和CA模型的转换,实现对运动目标更准确地跟踪[6]。VD算法是在二维卡尔曼滤波的基础上采用非机动模型和机动模型2种模型,当检测到无机动时滤波器工作于正常模式(即非机动模型),当检测到机动模型时,立即增加一个状态变量,用机动模型跟踪目标,直到下一次判决而退回到正常的非机动模型。
机动目标跟踪原理框图,如图1所示。首先,通过雷达或其他测量系统所获得的实时位置数据来判断目标的机动状态,根据机动状态进行滤波模型的调整转换,当检测到机动状态发生变化后,进入加速模型开始对滤波系统的状态估计进行调整,输出目标的加速度、速度和位置信息,同时,将这些信息反馈之输入信息,不断迭代和调整加速度、速度和位置信息。

图1 机动目标跟踪原理框图
1.2.1 机动目标检测
在对系统的参数进行初始化后,开始对运动目标进行跟踪,当检测到跟踪目标的状态发生变化时,调整目标的运动模型[7]。
对于跟踪目标的状态检测,可以通过这几个参量来判断:雷达或其他测量系统所获得的实时雷达位置xl(k)、时长为s的滑动测量测量窗口ρ、俯仰角ω(k)、以及检测常量θ。
ω(k)=Δxl(k)△ρ
(11)
运用式(11)可以通过雷达或其他测量设备返回的数据不断地得到ω(k),再依次观察2个相邻的ω(k)之间的变化△σ。
△σ=ω(k)-ω(k-1)
(12)
一旦△σ的变化大于了系统所设定的检测常量θ,这时认为跟踪目标已经发生机动,状态已经发生了变化。
1.2.2 自适应调整参数
检测到机动发生后,开始对滤波系统的状态估计进行调整[8],从而实现自适应机动目标运动状态的目的。
假设滤波器每次检测的窗口长度为s,每隔s秒就检测一次物体的位置,会更倾向于相信雷达返回的数据,而不是滤波器。因为有部分滤波器在跟踪物体进行非线性运动时会出现较为明显的误差。假如在第k次检测时检测到跟踪目标发生机动,则认为在k-s时刻到k时刻中有一恒定加速度加入到滤波器中,跟踪目标开始发生机动,此时需要对滤波系统的状态估计进行修正[9-11]。下面以跟踪目标在x轴方向上的状态为例,给出具体参数调整方法。
由于k时刻的位置是基于雷达返回的数据得来的,需要将k-s时刻到k时刻的加速度先求出来,然后再根据加速度去将跟踪目标的运动状态模型(CV模型)更新成加速模型(CA模型)。
k-s时刻到k时刻跟踪目标的加速度估计为式(13):
a(k|k-s)=2[xl(k)-xl(k-s)-ω(k-s)]/s2
(13)
k时刻跟踪目标的速度估计为式(14):
v(k|k-s)=v(k-s)+t·a(k|k-s)
(14)
k时刻跟踪目标的位置估计为式(15):
x(k|k-s)=x(k-s)+t·v(k|k-s)+
a(k|k-s)t2/2
(15)
以上3步操作相当于是更新了式(5)~式(7),后面的公式按照1.1.2章节所述步骤的顺序进行迭代就可以了。
2 仿真分析
假定在一个平面坐标有一个雷达对机动目标进行观测,跟踪目标从坐标的原点开始出发,在t=0~11 s,跟踪目标沿着X轴方向,做速度为15 m/s的匀速直线运动;在t=11~20 s,X轴受到一个大小为5 m/s2的恒定加速度加入,在t=20 s时目标结束运动。雷达每隔1 s进行一次扫描,对跟踪目标进行观测,其中雷达的观测噪声的标准差为4 m,时长为1的滑动测量测量窗口ρ。本文仿真分别用经典卡尔曼滤波算法、自适应卡尔曼滤波算法、α-β滤波算法和自适应α-β滤波算法,得出结果进行比较。
跟踪目标做了一次匀速运动和加速运动,符合目标的预设轨迹。当跟踪目标处于匀速运动状态,4种滤波算法对机动目标的跟踪效果都非常好。但是当机动目标开始进行变速运动时经典卡尔曼滤波和α-β滤波的滞后性就会使跟踪目标与真实位置的误差慢慢变大,如果跟踪目标继续进行非线性运动,那么它的误差也会越变越大。α-β滤波与经典卡尔曼滤波在跟踪目标后一段时间,已经出现了较为明显的滞后,这意味着这2种算法无法较为有效的跟踪机动目标。而自适应卡尔曼滤波与自适应α-β滤波在目标进行状态转换后会出现误差,但这种误差会随着时间的推进而慢慢减小,从而获得一个较好的跟踪图像。目标跟踪X坐标误差的最小值和最大值,见表1。
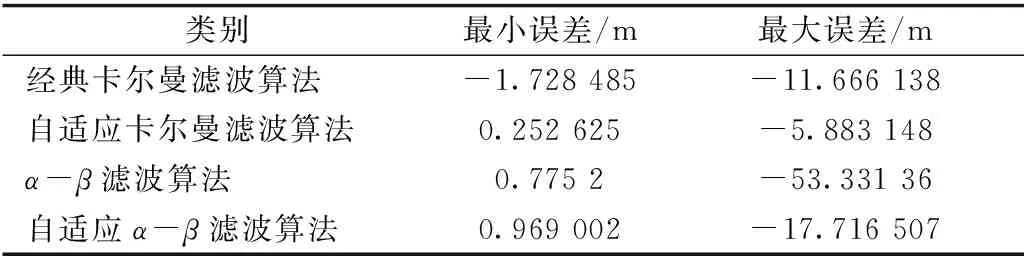
表1 目标跟踪X坐标误差的最小值和最大值
从表1可以看出,自适应α-β滤波算法的最大误差相较于α-β滤波算法的最大误差是有着较大的改善的。卡尔曼系列的最大误差相对于α-β系列的最大误差会小,但是卡尔曼系列滤波的计算量比α-β系列滤波的计算量大很多。
仿真计算出各算法与真实位置之间误差的绝对值,从各算法与真实位置之间的误差的绝对值来看,对于α-β滤波算法,当跟踪目标在进行匀速运动时它可以较为准确的跟踪,一旦跟踪目标的模型发生机动,它也会产生较大的误差。α-β滤波与经典卡尔曼滤波比较,其计算量小于卡尔曼滤波,但误差远大于卡尔曼滤波算法。而在使用了自适应α-β滤波算法之后,可以看到原来α-β滤波在非线性运动时产生的误差已经被减小许多了,而且它的计算量小于卡尔曼滤波算法,因此跟踪效果比卡尔曼滤波效果要好。
各算法仿真运行时间指的是将这4种算法各进行一次仿真,记录从运行开始到以上滤波的运动图生成之间的时间,见表2。可以通过记录这段时间来侧面看出计算量之间的大小,也可以很直观的看出α-β系列滤波的计算量是小于卡尔曼系列滤波的。由于运算量较小所看到的差异不是特别大,而一旦应用于实际工程中,运行时间差距会进一步被放大[12]。

表2 各算法仿真运行时间
3 结语
综上所述,自适应α-β滤波算法是针对经典α-β滤波跟踪复杂的目标运动时会产生较大误差所提出的,它是基于α-β滤波与α-β-λ滤波,通过俯仰角ω(k)和检测常量θ来实现跟踪物体的模型切换,从而得到一个更为精准且计算量较小的跟踪轨迹。本文用经典卡尔曼滤波算法、自适应卡尔曼滤波算法、α-β滤波与自适应α-β滤波进行仿真实验,在多重模型的比较下实验表明:自适应α-β滤波算法对于机动目标的跟踪要优于α-β滤波算法,虽然精度不足卡尔曼滤波系列,但是在加速阶段可以看到自适应α-β滤波的精度已经稍优于经典卡尔曼滤波,同时α-β滤波系列的计算量远小于卡尔曼滤波系列,更适合于实际工程中的应用。
