基于IHBA的全电驱船能量管理策略研究

徐大勇，赵 杨，舒方舟，闫 羲，戴晓强

（1.海军装备部驻南京地区第一军事代表室，江苏 南京 210006；2.江苏科技大学 自动化学院，江苏 镇江 212100）

0 引言

近年来，世界范围内对低碳式发展的呼声愈演愈烈，各行业的“绿色转型”已成为国际共识［1-2］。由于船舶具有载货量大、可远洋航行等优点，使航运业成为了国际经贸合作中的重要一环，但在保障全球物资流动的同时，船舶消耗了大量化石燃料。据英国劳氏船级社统计，目前航运业的二氧化碳年排放量占全球总量的2.33%，硫氧化物、氮氧化物年排放量占比分别为20%与30%［3-5］。

随着电力推进、电能存储与新能源发电技术的发展与成熟，逐步提高的排放限制要求，造船业面临着更换船舶主要动力来源的问题［6-7］。相较于使用内燃机、蒸汽机和汽轮机等传统能源的船舶主机，使用电动机作为全电驱船的主动力装置后，电能便成为了连接全部船载电气装置设备的纽带。因此，船舶电网的电能流动情况，将直接影响船舶航行动力。

为了在完成预期航行任务和保证船舶动力供应的前提下，降低航行过程中的运营成本，减少污染排放，应充分协调电网的各分布式电源工作状态，优化各船载设备调度计划。国内外已有相关学者对此开展研究，Kalikatzarakis等［8］基于等效能耗最小化策略与动态规划方法实时优化船舶行进策略，降低了约6%的燃油消耗成本。肖能齐等［9］基于工况识别的规则型能量管理策略，实时调节各船载设备的当前工作状态，节省了船舶燃油成本，减少了污染排放。印波等［10-13］针对同一个能量管理优化问题，通过改变算法机制提升能量管理策略的优化幅度，但并未结合优化问题本身改进算法机制。随着新能源发电装置的应用与推广，使船舶电网中的电能供给形式增多，导致上述调度工作的复杂程度呈指数规模上升，现有能量管理策略的制定方式难以应对上述变化。

综上，本文基于全电驱船的电网模型构建能量管理策略的实时优化模型，分析模型实际需求后使用蜜獾优化算法驱动模型（Improved Honey Badger Algorithm，IHBA）优化能量管理策略。此外，根据优化问题的实际特征改进标准算法，通过仿真实验验证所提方法的有效性与先进性。

1 全电驱船电网模型

图1 中全电驱船的电网模型主要由分布式电源、电力推进系统、其他电气负载3 部分组成。分布式电源包括柴油发电机（Diesel Engine，DE）、光伏发电设备（Photovoltaic Generation Equipment，PGE）、蓄 电池 组（Storage Battery Pack，SBP）、超级电容器（Supercapacitor，SC）、岸电供给设备（Shore Power Equipment，SPE）、电力推进系统（Electrical propulsion system，EPS）。EPS 包含推进电动机、螺旋桨等；其他电气负载（Load，L）指除电力推进系统外的全部电气负载，电网各装置数学模型可参考文献［10］。

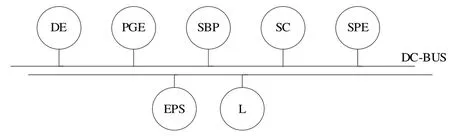
Fig.1 Power grid model of all electric ship图1 全电驱船电网模型

为提高研究成果的可扩展性与推广价值，全电驱电网模型包含了4 类不同工作特性的分布式电源，基本涵盖了目前的主流船用电源［14-16］。柴油发电机代表具有稳定输出能力，但发电过程伴有污染排放情况的一类电源；光伏发电设备代表出力情况受限于外界环境，具有波动性与间歇性的一类电源；蓄电池组代表供电能力有限，能量密度高、功率密度低的一类电源；超级电容器代表供电能力有限，能量密度低、功率密度高的一类电源。

2 能量管理策略的实时优化模型

全电驱船的实时优化模型由4 部分组成：能量管理策略即为优化变量；优化变量的评价指标即为目标函数；优化变量的取值范围即为约束条件；优化变量的求解方法即为优化算法。

2.1 优化变量

能量管理策略的实时优化模型与全电驱船能量管理策略的全局优化过程相似，需要优化分布式电源的出力方案［17-19］，但两者不同之处在于：

（1）船舶航行特性决定了它并不需要频繁、主动调整实时航速，在绝大部分航行时间内将处于巡航状态，因此在本文所建立的实时优化模型中，航速将不再作为优化变量，而是令船舶在既定航速下保持巡航状态。

（2）实时优化模型不再需要优化全航程内的各分布式电源的工作状态，因此本文建立的实时优化模型的优化变量被设置为由1 小时航时内的全电驱船中各分布式电源的出力方案组成，即每分钟的柴油发电机的输出功率PDE(t)、蓄电池组的输出功率PSBP(t)和超级电容器的输出功率PSC(t)。

综上所述，在相同的全电驱船电力系统模型条件下，实时优化模型相较于全局优化模型，优化变量与分量个数更少，但实时优化任务对算法运算速度提出了更高要求，即实时优化模型应具有快速响应特性。

2.2 目标函数

式中，S1、S2、S分别为经济成本、排放成本和总成本。

总成本S为优化模型的总优化目标，经济性目标S1由柴油发电机的使用成本CDE、蓄电池组的使用成本CSBP和超级电容器的使用成本CSC组成，排放成本S2为全电驱船航行过程中的排放废气总量EDE。

（1）柴油发电机使用成本。

其中，price为柴油油价，Vfuel为柴油发电机的燃油消耗量，α(·)为柴油发电机的运维费用系数，是负荷率LFH的函数。

（2）蓄电池组使用成本。

其中，CDeg，SBP为蓄电池组的衰退损耗费用，βSBP为蓄电池组的衰退损耗系数，BCD为蓄电池组的充、放电交替循环系数，BE为蓄电池组的过量使用幅度。

（3）超级电容器使用成本。

其中，CDeg，SC为超级电容器的衰退损耗费用，βSC为超级电容器的衰退损耗系数，CCD为超级电容器的充、放电交替循环系数。

（4）废气的环境成本。

其中，ξi为船用柴油发电机消耗燃油时排放的大气污染物中不同污染气体的转换系数。

由于本文所构建的优化模型需要具备快速响应特性，而基于Pareto 支配关系的多目标处理方法计算耗时较长。为此，将式（1）简化为：

其中，E'DE为全电驱船所排放废气的环境治理成本，ζi为各种气体的单位体积治理成本。

综上所述，通过式（6）、式（7）将多目标问题简化为单目标问题，进而使实时优化模型满足快速响应特性的需求。

2.3 约束条件

（1）功率平衡约束。

式中，PDE(t)、PPGE(t)、PSBP(t)、PSC(t)分别表示t时刻的柴油发电机、光伏发电设备、蓄电池组和超级电容器的输出功率。由前文可知，本文所建立的优化模型岸电供给设备的输出功率PSPE(t)恒等于零，PEPS(t)、PL(t)分别为电力推进系统和其他电气负载的功率需求。

（2）分布式电源输出功率约束。

（3）储能装置容量约束。

（4）爬坡功率约束。

式中，PDE(t)、PDE(t+1)分别为柴油发电机在第t、t+1 时刻的输出功率，PSBP(t)、PSBP(t+1)分别为蓄电池组在第t、t+1 时刻的输出功率，ΔPDE、ΔPSBP分别为柴油发电机和蓄电池组的爬坡功率，PDE，limit、PSBP，limit分别为柴油发电机和蓄电池组的最大爬坡功率。

2.4 优化算法

本文使用集群智能算法驱动实时优化模型，优化船舶能量管理策略。虽然，现阶段存在诸如粒子群算法（Particle Swarm Optimization，PSO）等广泛应用的集群智能算法，但应自身更新机制特点限制，PSO 的优化过程普遍会陷入停滞状态，浪费了大量的计算算力。

本文将PSO 应用于优化模型后，优化过程曲线显示确实存在停滞状态，因此PSO 无法应用于本文研究之中。此外，由NFL 定理可知，直接在新研究问题中套用集群智能算法的现有研究成果会产生不适应性；反之，在集群智能算法的实际应用过程中，更适合针对性地挑选标准算法改进适应性。

综上所述，在集群智能算法应用与本文所研究的优化问题中，需要在部分标准算法中进行测试，选择能成功应用的标准算法，结合研究问题的具体特征对算法机制进行改进，即由一种泛化能力（Generalization Ability）强的标准算法得到一种特化能力（Specialization Ability）强、针对性好的算法，从而提升算法的优化幅度。

3 蜜獾优化及其改进算法

3.1 蜜獾优化算法

蜜獾优化算法（Honey Badger Algorithm，HBA）基于蜜獾对蜂蜜的搜索与采集行为而提出的一种群体智能的演化计算方法［20-24］，具体流程如图2所示。

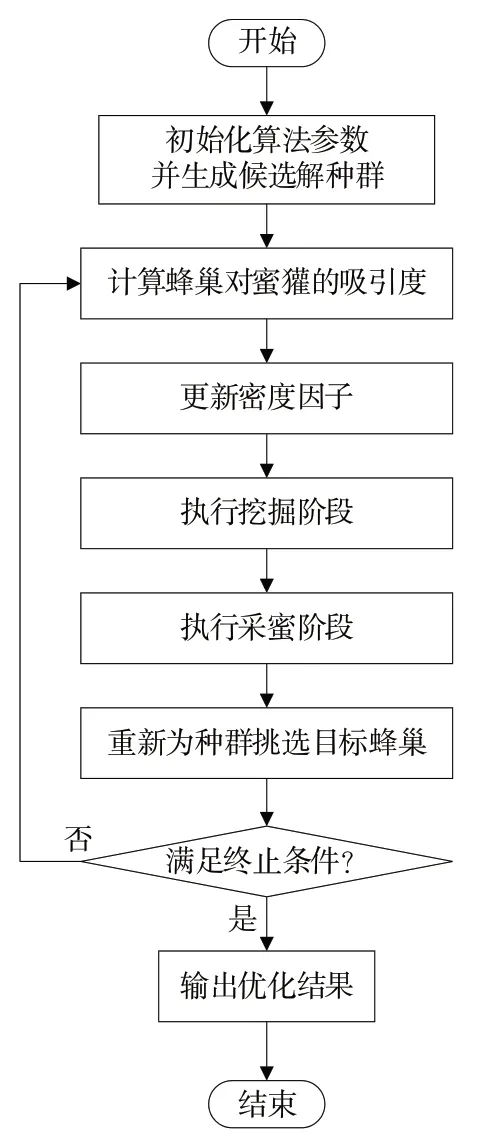
Fig.2 Flow of honey badger algorithm图2 蜜獾优化算法的流程

步骤1：算法参数初始化，生成初始候选解种群。

步骤2：设置蜂巢对第i个个体xi的吸引度Ii。

式中，xprey为蜂巢所在位置，rand为随机数。

步骤3：更新密度因子α。

式中，it、MaxIt分别为当前迭代代数和最大迭代代数，C为常数系数。

步骤4：选择行为模式。个体随机地选择行为模式，进入挖掘阶段或采蜜阶段。

挖掘阶段：

式中，F为搜索方向标志，β指蜜獾获取猎物的能力。

采蜜阶段：

步骤5：重新定位蜂巢。此时，种群评价最高的个体的位置即为新蜂巢位置。

步骤6：是否满足结束条件？若满足则执行步骤7。否则执行步骤2。

步骤7：结束运算，输出结果。

3.2 改进蜜獾优化算法

通常，集群智能算法对运算过程的实际时长不敏感，但对相对时长较为敏感，即当前迭代代数与最大迭代代数所表征的算法运行时间的相对值。为适应优化模型的快速响应特性需求，本文设计了一种时间尺度下的HBA 改进算法，提高迭代初期的搜索能力并加速搜索过程。

3.2.1 改进密度因子αS

由于集群智能算法的更新机制普遍存在强随机性，即便在相同参数设置下，每次迭代运算时长具有不确定性。为满足优化模型的快速响应需求，需要在其运算时间达到限值后，立即停止运算并输出当前的最优结果。

为此，IHBA 将核心参数密度因子由原本的随迭代代数变化方式，改进为随仿真时间变化的方式。如式（18）所示，随着运算过程进行，算法通过改变密度因子αS值，逐渐让搜索由全局探索转变为局部开发，使算法在既定仿真时限内，迅速完成搜索倾向转变，加速算法整体运算过程。

式中，time、TIME分别为当前仿真时间和最大仿真时间。

3.2.2 改变行为模式选择方式

根据分析算法更新机制，在HBA 中个体行为模式差异将导致搜索倾向发生变化。因此，IHBA 将改进个体行为模式的选择方式，使个体在算法迭代过程的不同时期能拥有适宜的搜索倾向。

在HBA 中个体根据概率随机选择，即每次选择行为模式时挖掘阶段和采蜜阶段的概率各占1/2。但在IHBA 中，个体将按优化问题实际需求选择行为模式。由于本文所研究的优化问题存在约束条件，在仿真开始后算法首要目标应寻找可行解，则个体的行为模式应以挖掘阶段为主，即此时算法更倾向于全局探索解空间，试图快速寻找可行解，保证算法结束运行后至少能输出可行的优化方案。

随着仿真持续进行，算法的首要目标转换为优化当前种群中的可行解，受仿真时间限制，算法无需再从解空间中寻找新的可行解再进行优化，而是应在有限的剩余时间内对现存可行解进行优化，因此算法需要快速转换为以采蜜阶段为主，即此时算法更倾向于搜索现有可行解周边区域，寻找可能存在的更优质的解。IHBA 中个体选择行为模式的概率计算方式为：

式中，pro为个体以挖掘阶段作为其行为模式的选择概率，选择采蜜阶段作为行为模式的概率为(1-pro)，r*为挖掘阶段的初始选择概率，设定为固定常数且r*∈(0，1)。

4 实验结果与分析

4.1 算例设置

全电驱船的预期航速恒定为12.52 海里/h，其他电气负载的功率需求曲线如图3 所示。仿真实验的模拟航行时长为1h，单位时间长度为1min。

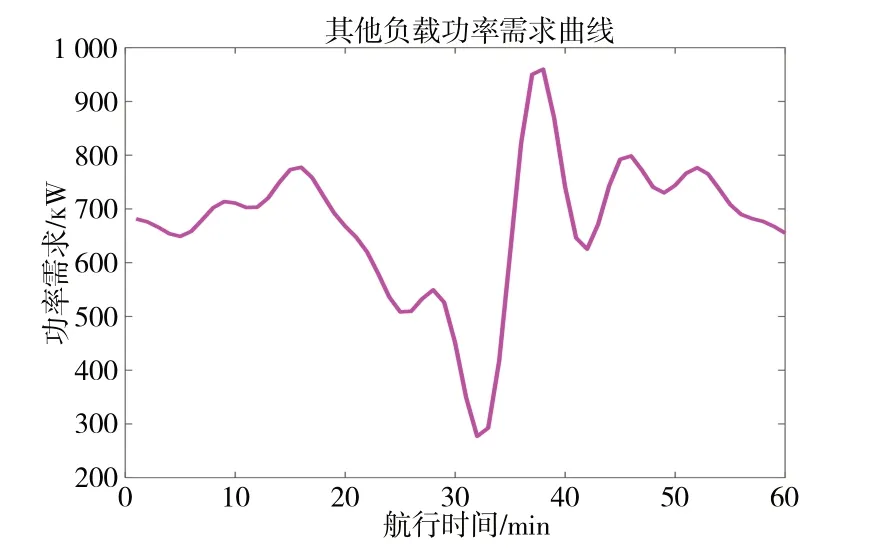
Fig.3 Curve of power demand of other electrical loads图3 其他电气负载功率需求曲线

船舶在航行过程中不可避免地会受到波浪、海风等水文要素影响，所受阻力可分为水和空气阻力。其中，水阻力占主要部分［25］。由于本文求解的是实时优化问题，无法忽略阻力对船只及推进系统的影响，当船舶处于巡航状态时，实际推进功率并非为一个既定航速所对应的固定值，因此推进系统会做一部分功克服船舶所受的阻力。

本文将航行水域的风浪等级分为3 级，不同等级下的实际推进功率曲线如图4所示。其中，“风浪等级I”代表此时航行水域风浪等级较小；“风浪等级II”代表此时航行水域相对平静，但偶尔会出现较大风浪；“风浪等级III”代表此时航行水域风浪等级较高。为体现光伏发电设备受环境因素限制而产生的输出波动性，本文按照光照强度将光伏发电设备的输出能力划分为3 个等级。具体的，当光照强度较高时，令PPGE(t)=800 kW 并标识为“A”；当光照强度一般时，令PPGE(t)=600 kW 并标识为“B”；当光照强度较低时，令PPGE(t)=200 kW 并标识为“C”。

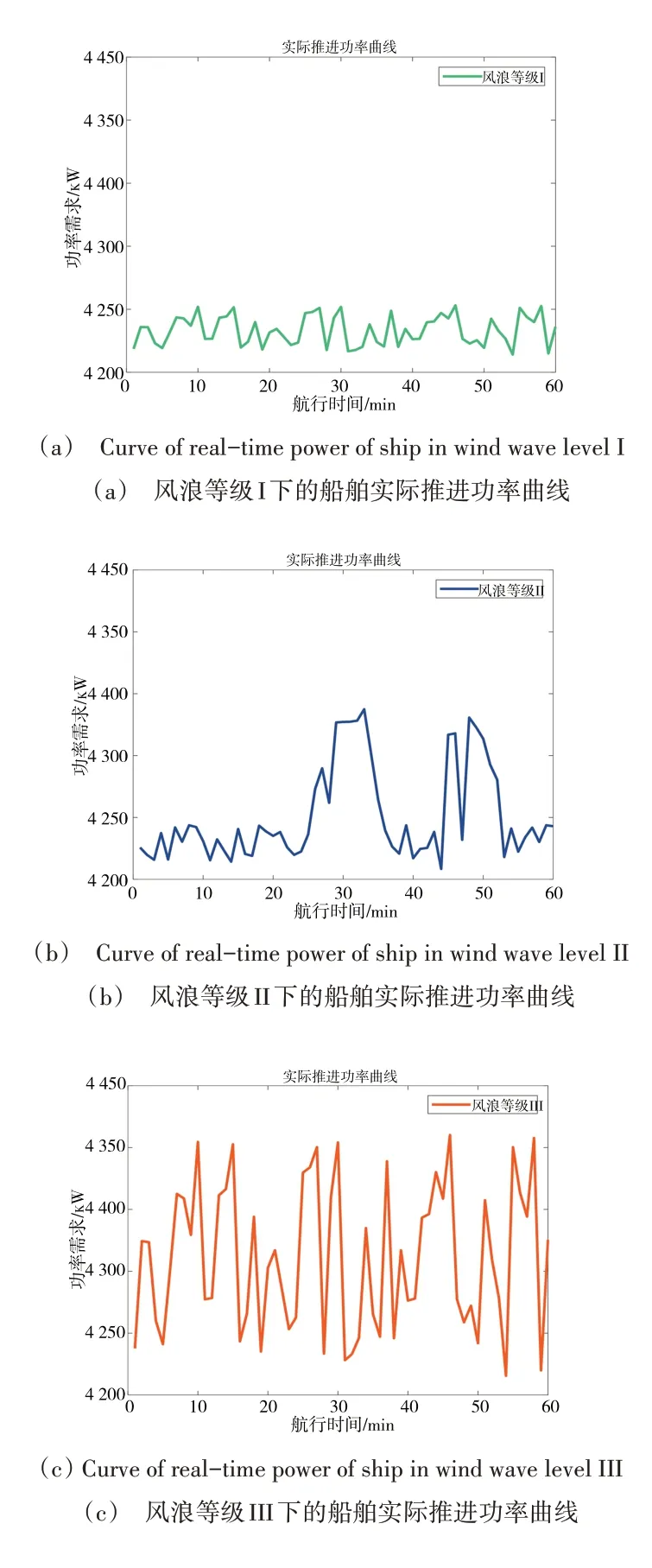
Fig.4 Curve of real-time power in different wind-wave level图4 不同风浪等级下的船舶实际推进功率曲线

为体现环境因素对全电驱船能量管理策略的影响，本文结合风浪等级与光照强度生成9 种典型航行场景，分别得到该场景下的实时优化结果见图5。其中，“A-I”表明此航行场景的光照强度较高且航行水域风浪等级较小。

4.2 结果分析

图5 为在9 种典型场景下，IHBA 与HBA 的优化过程比较，部分图中信息需要额外说明：

（1）为体现优化模型的快速响应特性，本文在评估算法性能与比较优化结果时，将以实际仿真时间作为横轴元素，而并非为常用的迭代代数。由于使用迭代代数作为横轴元素时，相同横坐标值下的纵轴数据忽略了每次迭代计算过程中的算法复杂度差异。换而言之，评价更高的结果可能需要更多算力资源，导致比较标准算法与改进算法在相同迭代代数后的性能差距有失公允。为此，本文使用实际仿真时间作为横轴元素，在基于控制变量原则、使用同一配置的计算机进行仿真实验时，通过图5 直观比较两种算法的性能差距，并且相同横坐标值下、不同算法的纵轴数据所需算力资源相同，从而使得比较结果真实可信，并且整个过程算法的复杂度为0。

（2）由于经济成本S1与排放总量EDE的数量级相差较大，为直观、清晰展示算法的优化过程，以首个最优解数值为基础归一化处理数据，因此每条曲线起点的纵坐标皆为100%。

（3）线型较粗的线条代表HBA 的优化过程，线型较细的线条代表IHBA 的优化过程，实线线型的线条代表归一化的经济成本S1，虚线线型的线条代表归一化的排放总量EDE。

如图5 所示，在C-I、C-II 和C-III 中，子目标更新曲线无法保持单调递减，表明优化过程中虽然部分当前最优解的总目标函数值低于时间更早的最优解，但前、后者互不Pareto 支配，即前者的两个子目标评价未能同时相较于后者更高。此时，模型受限于优化模型的快速响应特性需求，只能按式（6）、式（7）方式牺牲解的支配水平而提高模型总体运算速度。

本文以图5 中A-I 的优化过程为例，展示了两种算法的优化结果比较情况（见图6）。由此可见，IHBA 较大幅度地调节了柴油发电机的出力情况，仅微调了蓄电池组与超级电容器的出力情况，从而使其经济成本S1明显下降，成本S2仅存在微小降幅，总航行成本S相较于HBA 降低了13.40%。

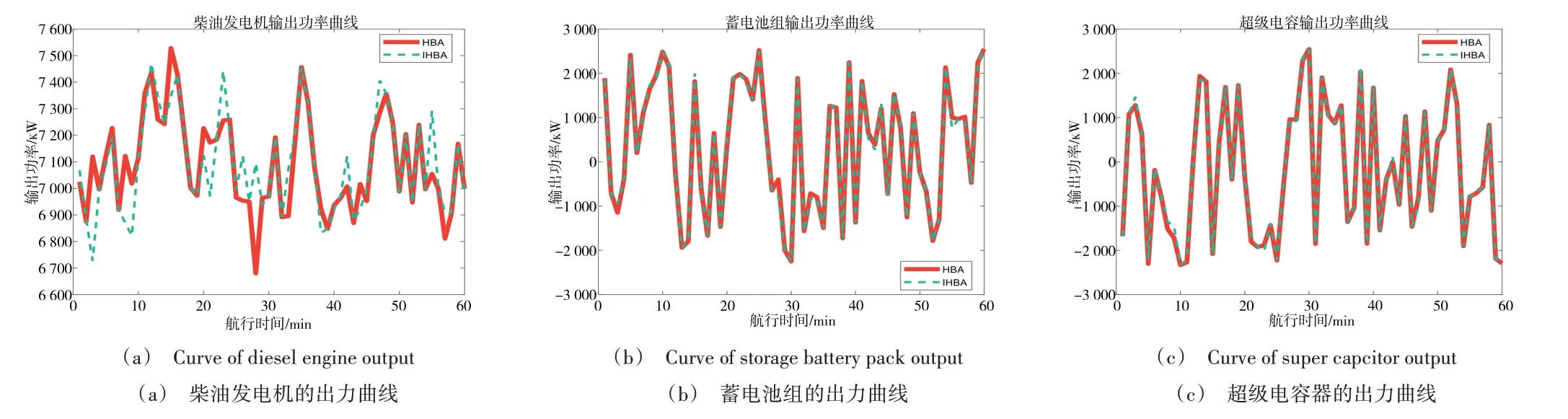
Fig.6 Curves of each distributed generation output图6 各分布式电源出力曲线

综上所述，实时优化模型在应用IHBA 后实现了预期目标，对HBA 的改进方法行之有效，原因可能为：

（1）密度因子αS控制着算法的搜索倾向，IHBA 基于最大仿真时间和当前仿真时间，使密度因子αS在迭代过程中恰当地转变搜索倾向。如前文所述，在迭代代数相同的情况下，每次HBA 仿真时间均会存在一定的差异，在计算密度因子αS时又依赖于最大迭代代数MaxIt，因此难以设置合适的MaxIt数值，导致算法在仿真末期难以拥有适当的密度因子αS。通过式（18），IHBA 能自动适应由仿真时长限制所带来的影响，恰当地在迭代过程中调整密度因子αS的取值。

（2）实时优化模型的快速响应特性需求，要求其所使用的优化算法能在迭代早期更倾向于在解空间中全局探索，以至少得到一个可行解，然后快速集中算力局部开发现有可行解。对于本文所构建的实时优化模型而言，其快速响应特性需求限制了算法的发挥空间。在此问题中，HBA 每次对个体行为模式的选择方式仅为依据概率二选一，在迭代过程中后期的全局探索行为浪费了相对有限的算法算力。然而，IHBA 通过改进个体行为模式的选择方式，将更适合本文研究的优化问题与构建的优化模型。

5 结语

本文在全电驱船电网模型基础上建立能量管理策略的优化模型，根据实际问题需求与特征，选择HBA 作为驱动算法，并对标准算法进行针对性改进。IHBA 中使用了实际仿真时长计算算法的核心参数密度因子αS，改变了个体行为模式的选择概率，使算法能在较短运算时长限制下，迅速调整搜索倾向完成搜索过程。实验表明，IHBA 能在HBA 的基础上进一步降低航行成本，使全电驱船的总航行成本S降低13.40%。

当前，国际海事组织等机构正逐步提高船舶排放限制要求，在后续研究工作中可通过结合惩罚措施调整排放成本S2中单位体积废气治理成本ζi的方式，因地制宜地调整全电驱船电力系统的调度计划，以满足不同航行水域的限制条款与环保要求。