基于伴随理论的无人机气动弹性优化
2023-10-31黄胤铮王晓喆王柳青
黄胤铮,王晓喆,王柳青
(1.北京航空航天大学 飞行学院;2.北京航空航天大学 无人系统研究院,北京 100083)
0 引言
无人机因具有体积小、成本低、对恶劣环境适应性好等优点,在民用和军用领域均有巨大的应用潜力[1]。但无人机的作战能力会受到飞机结构、气动布局、任务载荷、巡航时间等因素影响,无人机任务完成度以及生存概率也与其飞行性能和作战性能密切相关。随着航空技术的发展,未来空域的环境复杂度都会有不同程度的上升,对无人机的整体性能提出了更高要求。
随着有效载荷不断增加,无人机的结构重量系数不断下降,结构柔度不断增加,气动、结构等学科的耦合关系进一步增强,若在优化过程中采用串列优化方法会造成学科间的反复迭代,在降低设计效率的同时,也影响了整体性能的提升。气动弹性优化充分考虑了气动与结构之间的耦合效应,并以此挖掘设计潜力[2],实现飞行器在复杂环境下经济性和使用性能的提升[3]。在大型客机[4-5]和超音速客机[6]的设计中,气动弹性优化已经得到了较为广泛的应用。基于敏度信息的优化算法在求解大规模的多学科优化问题时,收敛较快[7-8],而以遗传算法为代表的进化式算法需要大量样本,不适合直接应用于多设计变量的气动/结构耦合优化问题中[9]。1988 年,Jameson[10]首次将伴随方程法应用于气动目标函数梯度的求解过程中,并对机翼进行优化设计。由于伴随理论的计算消耗与设计变量的数量无关,适合处理具有大规模设计变量的多学科优化问题,因此近年来得到了广泛关注[11-14]。Anderson 等[15]采用多学科建模优化方法和伴随理论,实现了风力涡轮机叶片的高保真结构优化和负载应力最小化;Wang 等[16]采用基于伴随方法的优化设计框架对机翼受动载荷进行了分析优化;Batay 等[17]采用多学科设计优化工具,结合伴随求解器,对风力涡轮机进行了并行气动设计优化;Wilke[18]采用自主开发的多目标优化框架实现了对直升机旋翼桨叶的优化设计;李润泽等[19]在多目标优化过程中结合伴随方法,提高了超临界机翼气动优化设计效率;刘晓东等[20]采用基于伴随理论的气动优化设计方法,实现了飞翼布局飞行器的气动优化。
随着现代无人机对高机动以及长航时性能的需求不断提高,采用基于伴随理论的气动弹性优化方法深度挖掘多学科耦合所带来的设计潜力是必要且迫切的。本文结合涡格法和有限元分析法,通过松耦合的方式实现气动弹性分析,并基于序列二次规划和伴随理论开展非线性敏度优化。分别针对长航时和高机动两类典型无人机,以最小燃油消耗为目标,对机翼的气动外形和空间梁结构等参数进行优化设计,并对优化设计的结果进行对比分析。
1 气动弹性仿真
1.1 气动涡格法
对于飞行器的气动分析本质上是对空间N-S 方程的求解。涡格法在位势流方程的求解过程中较为常见,与空间N-S 方程的求解相比,利用基于求解位势流的气动计算方法能够以更高的计算效率对启动导数进行比较准确的求解[21]。
根据边界不可穿透定理,可以在控制点处添加马蹄涡与气动表面相切的条件,如式(1)所示。其中,CC为控制点处诱导速度的系数矩阵,Γ为每个涡线涡强组成的列向量,V∞为控制点来流速度矩阵,N为控制点处单位法向量。
通过求解式(1)可得到每个涡的涡流强度和气动力,如式(2)所示。其中,Fn为涡段上的升力,ρ∞为来流密度,V∞为来流速度,Vn为当前涡段中点诱导速度,Γn为当前涡段上的涡强。
涡格法涡线布置方法如图1所示。

Fig.1 Vortex lattice method vortex line layout method图1 涡格法涡线布置方法
1.2 结构有限元法
对于组成机翼的各部分而言,机翼上下表面的蒙皮主要承载机翼上的弯曲载荷,机翼的翼梁和副梁主要承载剪切载荷,蒙皮和梁共同承载扭转载荷。在分析过程中,将机翼翼梁简化为空间梁单元的有限元模型进行分析。空间梁单元的有限元模型如图2所示[22]。
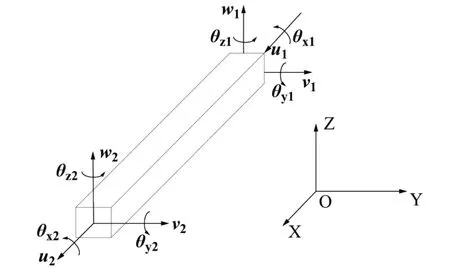
Fig.2 Finite element model of space beam element图2 空间梁单元有限元模型
通过对空间梁模型的分析,可以获得结构分析部分的控制方程如下:
其中,f为作用在节点上的力和力矩,d为节点位移列阵。通过求解式(3),可以得到各节点上的静力学载荷分布。
1.3 仿真模型
气动弹性的耦合求解采用松耦合方法,气动与结构之间的数据传递如图3、式(4)和式(5)所示[23]。

Fig.3 Aerodynamic load transfer图3 气动载荷传递
其中,i=1,2,分别代表气动网格对应有限元模型中的左右两个结构节点,T为气动网格上通过涡格法计算得到的合力,rsai为结构节点指向气动力作用点的方向向量,Fi、Mi分别为通过该牵引方案得到的节点力和节点扭矩。
在完成气动载荷传递后,通过有限元分析可以得到对应的结构位移,并传递回气动网格。
其中,i=1,2,分别代表气动网格对应有限元模型中的左右两个结构节点,di为平动位移,θi为转动位移,rsai同式(5),为结构节点指向气动力作用点的方向向量。在此基础上,结合开源框架OpenMDAO 建立无人机的气动、结构以及气动弹性耦合分析模型[24]。
2 优化算法及框架
2.1 伴随理论
传统的导数计算方法以有限差分法和复变量差分法为主,在梯度优化中,都需要对控制方程反复求解,计算量大。而伴随理论算法可以在保持精度的前提下,一次性求解出目标函数对所有设计变量的导数[3]。其计算量仅与目标函数和约束条件的数量有关,与设计变量的数量无关,适合多设计变量的优化设计问题。
本文的无人机气动弹性优化以气动结构耦合系统作为分析系统,以气动参数和结构参数作为设计变量。优化目标函数I和控制方程残差R可设定为:
其中,x表示设计变量;w、u表示气动/结构耦合系统状态变量,其中w具体表现为涡格法中网格单元的气动负载,u具体表现为有限元分析中结构有限元分析得到的结构位移;Ra对应气动分析的残差,Rs对应结构分析的残差。
令优化目标函数I和控制方程残差R分别对设计变量x进行求导,并利用恒等变换和伴随算子ψ得到伴随方程。通过求解伴随方程,可以一次性求解出目标函数针对所有设计变量的导数,如式(8)所示:
2.2 序列二次规划
常用的梯度优化方法包括BFGS 拟牛顿算法、共轭梯度法、序列二次规划算法(Sequential Quadratic Programming,SQP)等。其中,序列二次规划法对大规模数据的计算效率较高,在工程中得到了广泛应用。具体形式如式(9)所示:
其中,f(x)为目标函数,h(x)为等式约束函数,g(x)为不等式约束函数。
序列二次规划法是一种用于求解非线性最优化问题的方法,其基本思路是将原问题转化为一系列二次规划(Quadratic Programming,QP)问题进行迭代求解。在每次迭代中,通过求解二次规划问题得到下一次迭代的值,直到序列{xk}收敛于极值点。具体来说,对于某一次迭代值xk,NLP 会被近似为该点处的二次规划问题。通过求解该二次规划问题,可以得到下一次迭代的值xk+1。随着迭代次数k的增加,序列{xk}将收敛于极值点[25]。本文采用SLSQP 算法(Sequential Least SQuares Programming),该算法是由Kraft[26]于1988 年提出的一种非线性约束优化算法,通过将优化问题转化为一系列线性或二次规划子问题,用于求解无约束或约束的非线性优化问题。具体来说,SLSQP 算法采用牛顿法求解每个子问题,并利用辅助函数法处理约束条件。
2.3 气动弹性优化框架
本文所采用的气动弹性优化框架如图4 所示。具体流程如下:①设定优化目标并设置目标参数,明确目标函数、约束函数、设计变量与状态变量等相关变量及数据;②根据初始数据建立气动和结构的物理模型;③对目标函数和约束函数关于所有设计变量的总梯度进行计算;④利用序列二次规划算法进行寻优;⑤通过不断更新气动和结构的物理模型,直至得到收敛解,完成优化设计。
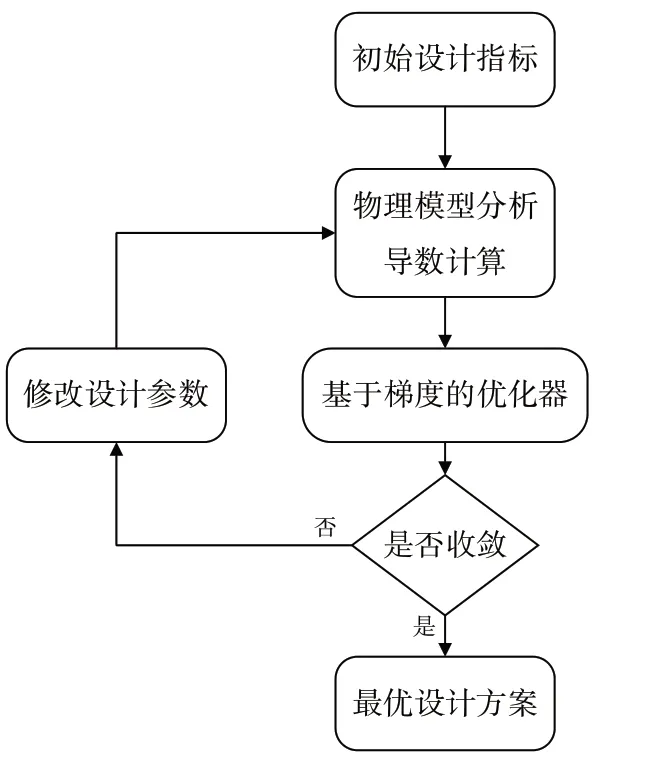
Fig.4 Basic process of optimization design based on gradient optimization algorithm图4 基于梯度优化算法的优化设计基本流程
3 无人机气动弹性优化
3.1 大过载无人机
在有人机上,8g是受过专业训练的航天员一般可以承受的最大过载[27]。而无人机没有相关限制,可以做出更多大过载的机动动作来规避潜在危险。
3.1.1 工况计算
大过载无人机具体的飞行工况如表1 所示。选取NACA0015 翼型,机翼初始参数如表2 所示,并选取7075 铝合金作为翼梁结构材料。

Table 1 High overload UAV flight state parameters表1 大过载无人机飞行状态参数

Table 2 Initial shape parameters of high overload UAV wing表2 大过载无人机机翼初始外形参数
目标函数为巡航状态下的燃油消耗量,对于飞机燃油消耗,采用Breguet 距离方程进行计算。具体方程形式如下:
其中,Wf为燃油重量,W0为飞机空重,Ws为结构重量,R为最大航程,V为巡航速度,SFC为燃油消耗率。设计变量为机翼梢根比、机翼后掠角、机翼扭转角、机翼翼梁厚度、机动状态下的机翼迎角。设计变量具体数量及数值范围如表3 所示。约束条件为:机动状态下机翼结构应力接近但不超过应力极限、机动状态下升力等于重力。

Table 3 Parameter range and number of design variables for high overload UAV表3 大过载无人机设计变量参数范围及数量
3.1.2 结果优化
经过优化设计后,可得到如表4 所示的3 种优化设计结果。无人机机翼的外形经过优化设计后的变化如图5所示。
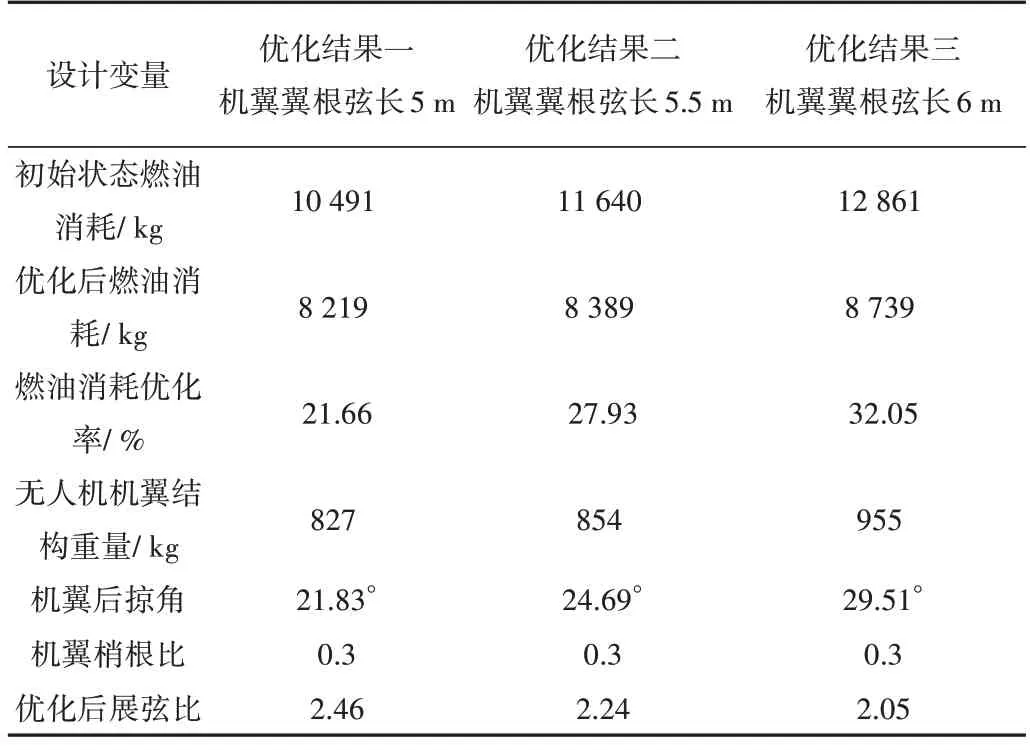
Table 4 Optimal design results of high overload UAV表4 大过载无人机优化设计结果
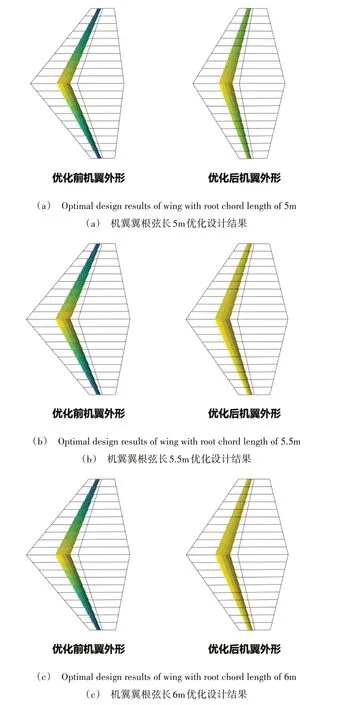
Fig.5 Optimal design results of UAV with different wing root chord lengths图5 不同机翼翼根弦长无人机优化设计结果
通过对不同机翼翼根弦长情况下机翼优化设计结果的综合分析,可以看出,在机翼经过优化设计后,大过载无人机的燃油消耗量相较于初始状态均降低了20%~30%。以机翼翼根弦长5.5 m 为例,如图6 所示,在经过优化设计后,可以看到冯米塞斯应力在巡航状态下远低于应力极限,符合基本逻辑和设计要求。在扭转角方面,机翼翼尖和翼根的相对扭转角为2.89°,符合机翼外形设计逻辑,改善了升力分布,有利于提升飞机的巡航性能[28]。设计方案总体上较为合理,符合飞行器机翼外形的设计逻辑。
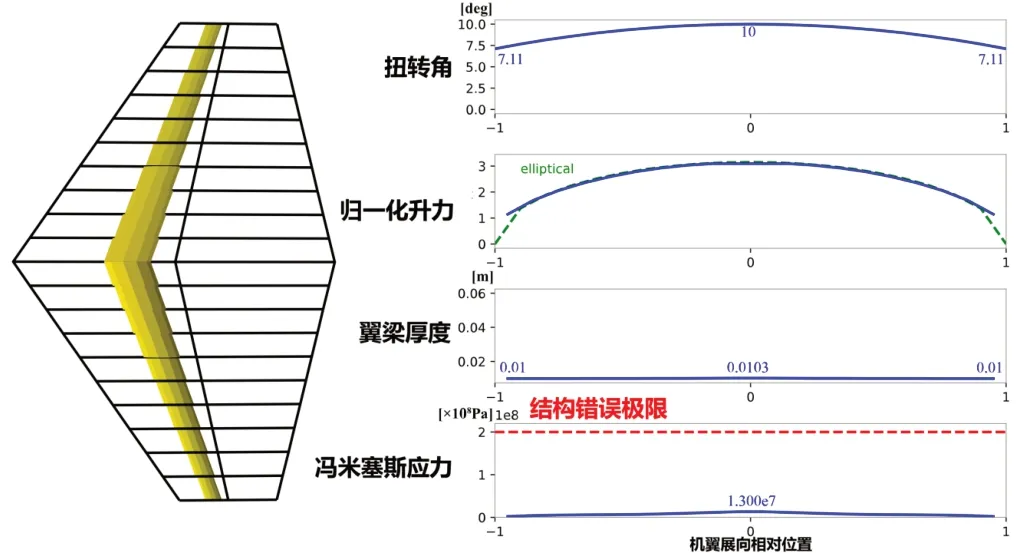
Fig.6 Optimal design results of wing with root chord length of 5.5m图6 5.5m机翼翼根弦长优化设计结果
3.2 长航时无人机
3.2.1 工况计算
对于长航时无人机,具体的飞行工况如表5 所示。选取NACA0015 翼型,采用如图7 所示的矩形机翼,初始参数如表6所示,并选取7075铝合金作为翼梁结构材料。

Table 5 Flight state parameters of long-endurance UAV表5 长航时无人机飞行状态参数

Table 6 Initial parameters of long-endurance UAV wing表6 长航时无人机机翼初始参数
目标函数为燃油消耗量,设计变量为机翼梢根比、机翼后掠角、机翼扭转角、机翼翼梁厚度、巡航状态下的机翼迎角。设计变量的具体数量及数值范围如表7 所示。约束条件为:机翼结构应力不超过应力极限、巡航状态下升力等于重力。
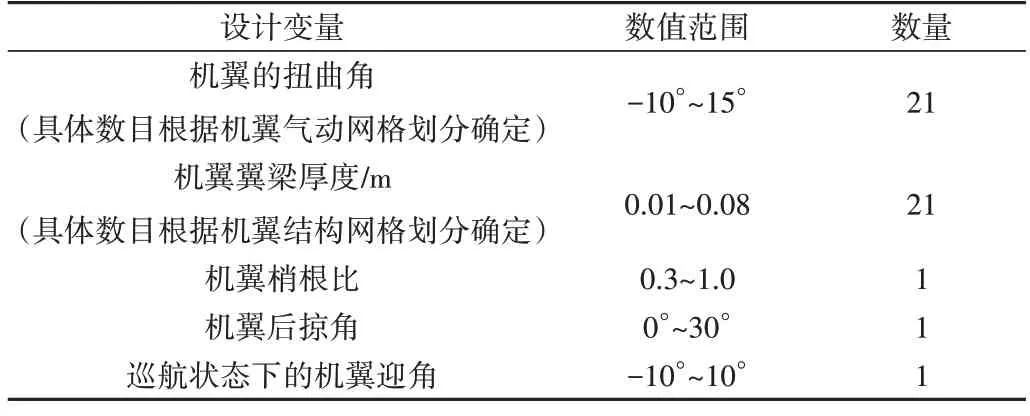
Table 7 Parameter range and number of high overload UAV flight status表7 高过载无人机飞行状态参数范围及数量
3.2.2 结果优化
长航时无人机优化后的机翼几何外形如图8所示。
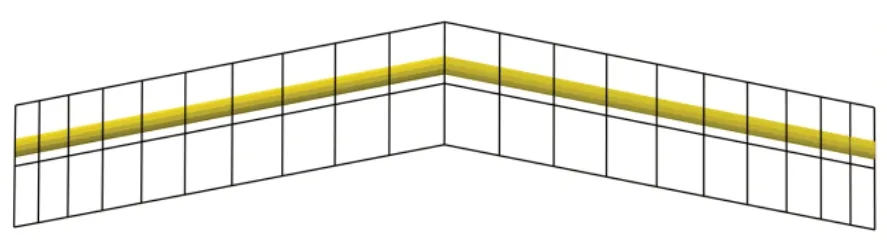
Fig.8 Optimized wing geometry of long-endurance UAV图8 长航时无人机优化后的机翼几何外形
初始状态下的燃油消耗量为3 898 kg,长航时优化后的燃油消耗量为3 004 kg,优化后的结构重量为1 761 kg。与初始状态相比,燃油消耗量降低了22.93%。优化设计后的具体参数如表8 所示。长航时情况下的优化设计结果如图9 所示。在扭转角方面,机翼翼尖和翼根的相对扭转角为5.15°,处于合理范围内。在冯米塞斯应力方面,由于需要获得最佳的优化设计结果,因此需要在设计过程中尽可能逼近结构极限。本文的优化设计方案未超出应力极限,符合飞行器外形设计逻辑。

Table 8 Optimized design results of long endurance UAV表8 长航时无人机优化设计结果
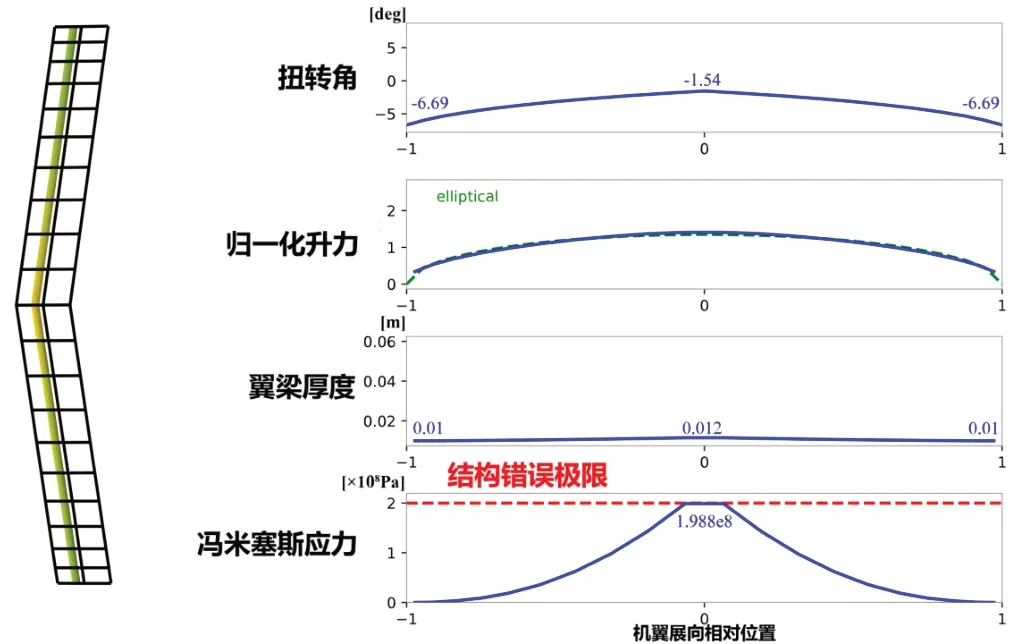
Fig.9 Optimized design results of long endurance UAV图9 长航时情况下的优化设计结果
4 结语
本文提出一种现代无人机的高效气动弹性优化方法,并通过大过载和长航时两类典型无人机进行了验证,具体如下:
(1)提出基于伴随理论的气动弹性优化方法,通过气动涡格法与有限元分析法进行气动弹性松耦合分析,并基于伴随理论和序列二次规划法进行非线性敏度优化。
(2)针对大过载无人机进行结构优化设计,以燃油消耗量为目标函数,以机翼外形参数和机翼翼梁结构参数为设计变量,结合机动状态下气动、结构两方面的约束函数,使无人机的燃油消耗量分别减少了21.66%、27.93%、32.05%。
(3)针对长航时无人机进行结构优化设计,以燃油消耗量为目标函数,以机翼外形参数和机翼翼梁结构参数为设计变量,结合巡航状态下气动、结构两方面的约束函数,使无人机的燃油消耗量减少了22.93%。
综上所述,本文提出的方法高效、稳健、可靠,时间成本和学习成本低,可为无人机气动弹性优化提供理论和方法参考。
