基于反步自适应分数阶PID的四旋翼控制

严云龙，姜文刚

（江苏科技大学 自动化学院，江苏 镇江 212100）

0 引言

四旋翼无人机是一种典型的欠驱动、强耦合的非线性系统，其结构相对简单、生产成本较低，在飞行过程中可以垂直起降，灵活改变姿态，并在固定位置悬停，因而在遥感、交通监测、救灾、环境监测、科研等领域发挥着越来越重要的作用［1-4］。

目前，四旋翼无人机的轨迹控制方法主要包括线性控制和非线性控制两种。PID（Proportion Integration Differentiation）控制［5］和LQ（Linear Quadratic ）控制［6］是两种结构简单的线性控制技术，然而这两种方法均需为四旋翼无人机系统提供高精度物理模型，当系统受到未知动力学的扰动时，其在轨迹控制方面的鲁棒性不尽如人意。反步控制［7］和反馈线性化［8］等非线性控制技术可以解决四旋翼无人机系统中固有的非线性和强耦合问题。然而当受控系统中存在不确定特性的干扰时，以上控制技术的性能得不到保证。为提高受到扰动时控制方法的鲁棒性，研究人员对PID 等线性控制策略进行了改进。例如文献［9］使用粒子群优化算法得到量化因子与比例因子，然后通过模糊化与反模糊处理动态调节权重因子，从而强化PID 的抗干扰能力。同时研究者们也提出大量非线性控制策略，包括鲁棒控制［10］、自适应控制［11］、神经网络控制［12］、滑模控制［13］、混合控制［14］等。

为解决复杂环境风干扰情况下的四旋翼控制问题，本文将反步控制理论、自适应控制理论与分数阶PID 控制理论相结合，设计了一种内外环采用不同控制策略的双闭环控制器，并通过仿真比较实验验证了其控制性能。

1 四旋翼无人机动力学模型

四旋翼无人机结构简单，主流形态为X 型，具体如图1所示。4 个电机是四旋翼无人机最重要的部分，飞行器通过4 个电机控制每个旋翼的转速以实现不同类型的运动。建立飞行器的动力学模型方程首先需要建立相应的参考坐标系［15］，分别为地面坐标系E0（O0，X0，Y0，Z0）和机体坐标系E（O，X，Y，Z），其中地面坐标系用于确定无人机的位置信息，机体坐标系用于衡量无人机的姿态。

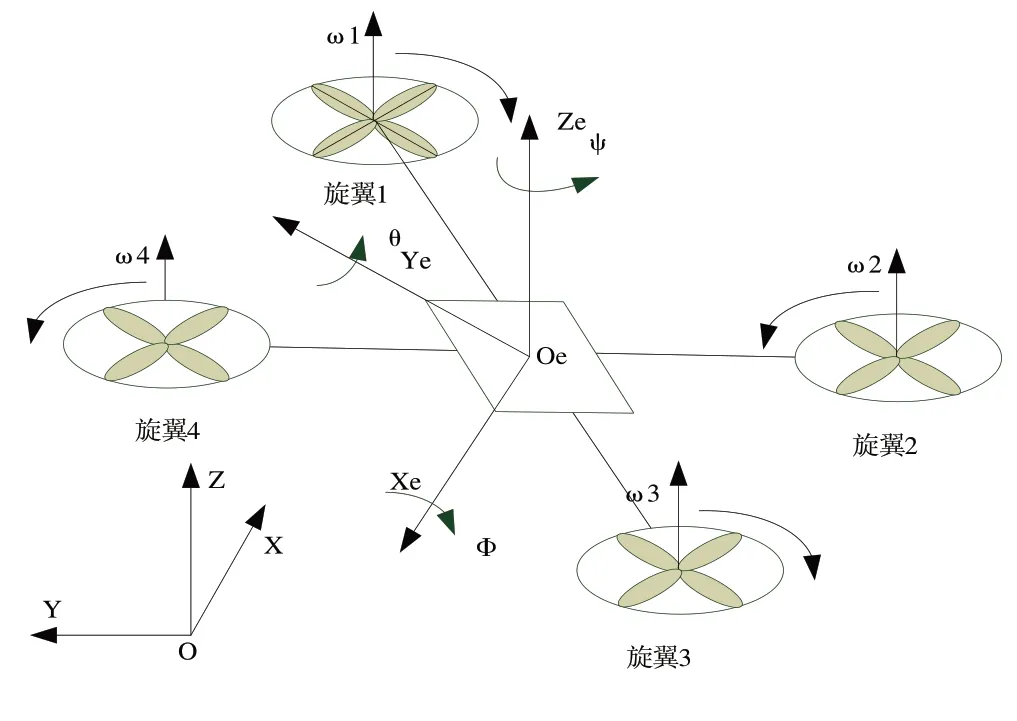
Fig.1 Structure of quadcopter unmanned aerial vehicle图1 四旋翼无人机结构

为建立科学而不过于复杂的四旋翼无人机数学模型，本文作出以下假设［16-17］：①四旋翼无人机为对称的刚体结构，机体坐标系的原点与机身质心重合；②不考虑四旋翼桨叶的弹性形变，四旋翼质心位置不受陀螺效应的影响；③飞行过程中所受空气阻力和重力不受飞行姿态的影响。

结合牛顿第二定律以及欧拉方程，建立如式（1）所示的四旋翼无人机数学模型：

式中：Ix、Iy、Iz分别为无人机绕X、Y、Z 轴的转动惯量；kx、ky、kz分别为无人机在飞行时的位置空气阻力系数；kΦ、kθ、kΨ分别为无人机在飞行时的姿态空气阻力系数；U1、U2、U3、U4为无人机的控制输入；di(i=1，2，3)为无人机飞行时各个坐标轴所受到的外界气流干扰。

2 控制方案

2.1 四旋翼控制系统结构

传统整数阶PID 控制算法仅为分数阶PID 的一种特殊情况，因此理论上分数阶PID 控制会有更高的上限。将整个飞行器控制系统分为内、外环两个回路，其中参照地面坐标系的位置控制作为外环路，以机体坐标系为基准的飞行器姿态控制作为内环路。然而两个贿赂参数都是固定的，无法响应外界干扰，又因四旋翼的姿态对其速度与方向有重大影响，故本文在内环采用反步自适应控制器，外环采用不完全微分的分数阶PID 控制器。基于改进反步自适应分数阶PID 的四旋翼无人机控制系统结构如图2 所示，其 中xd、yd、zd、Φd、θd、Ψd为期望的位置与姿态角，x、y、z、Φ、θ、Ψ 为实际的位置与姿态角，U1、U2、U3、U4为控制输入量。

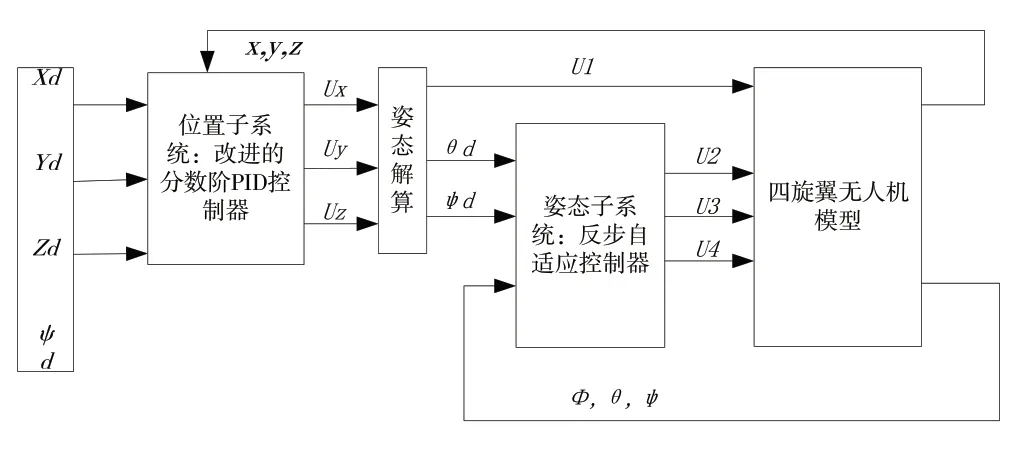
Fig.2 Four rotor UAV control system structure图2 四旋翼无人机控制系统结构

四旋翼无人机的非线性动力学方程可改写为状态方程的形式。表示为：

令Ux、Uy、Uz分别为四旋翼无人机在X、Y、Z 轴方向上的控制力，由式（1）可知，Ux、Uy、Uz与控制输入U1以及姿态角Φ、θ、Ψ的关系可表示为：

根据式（3）可以计算出U1与期望姿态角θd、Ψd。表示为：

2.2 外环分数阶PID控制器

分数阶微积分表达式为：

式中：m 和n 分别为分数阶微积分中积分的上限和下限；x 表示阶次可取任意实数，如果x 取整数，即表示整数阶微积分，反之则表示分数阶微积分。若x 大于0，nDm x表示微分，反之则代表积分。

本文采用Caputo 的分数阶微积分定义用于分数阶PID的算子［18］。具体表达式为：

式中：m-1 ＜a ＜m，m∈N。

传统整数阶PID 控制需要对比例、积分、微分3 个环节的参数进行整定，从而实现系统控制目标。分数阶PID 控制相较整数阶PID 控制拓宽了积分与微分环节的阶次范围，即增加了λ与μ两个控制参数，这意味着分数阶PID 控制有更广的控制范围，性能上限也更高。传统PID 控制引入微分信号虽然可以改善系统的动态性能，但也可能增强干扰的影响，尤其是环境风具有不确定性与突发性。因此，本文在分数阶PID 的微分环节增加一个低通滤波器，以降低阶跃信号带来的抖动影响，同时通过前馈控制器补偿扰动。改进后的分数阶PID 结构如图3所示。

Fig.3 Improved fractional PID structure图3 改进后的分数阶PID结构

在四旋翼无人机控制系统中，外环部分控制飞行器到达预定位置或沿预先设计的轨道飞行。在得到输入指令后，外环部分计算出预期姿态角，由内环姿态控制器追踪期望姿态角得出实际姿态角，从而实现位置追踪。改进的分数阶PID 控制器输出为：

式中：Kpm、Kdm、Kim（m取x、y、z）分别为各个坐标轴通道的比例、微分、积分参数；λ、μ分别为分数阶PID 的积分阶次与微分阶次；Tf为滤波器参数；Um(s)、Em(s)、Rm(s)、Gm(s)（m取x、y、z）分别为各个坐标轴通道的控制量、输入与输出误差、输入量以及系统传递函数。

2.3 内环反步自适应控制器

定 义Xd=[Φd、θd、Ψd]T为期望姿态角向量，X=[ϕ、θ、ψ]T为实际姿态角向量，E1=Xd-X为姿态误差向量。由式（2）可得：

根据Lyapunov 稳定性理论，选取正定的Lyapunov 函数V1。表示为：

对式（9）求导，得：

定义速度跟踪误差为：

式中：K1=[k1，k3，k5]T，k1、k3、k5 均为大于0 的常数。由此构造二阶Lyapunov 函数V2，可得：

对式（12）求导，得：

将式（14）代入式（13）中，得：

定义新的Lyapunov 函数V3为：

式中：λ为常数向量，λ=［λ1，λ2，λ3］T。

对式（16）求导，得：

2.4 外界自然风干扰模型

四旋翼无人机易受外气流干扰，最常见的气流为自然风。自然风具有突发性、持续性、周期性和不确定性等特点，需要考虑多种情况。参考文献［17］中介绍的包含基本风、渐变风、随机风的风场，建立其对四旋翼无人机的干扰模型。

基本风表示为：

渐变风表示为：

随机风表示为：

式中：v为基本风的风速，vmax为渐变风的瞬时最大风速，vmax2为随机风的瞬时最大风速，ωn分别为ϕ、θ、ψ。

综合上述3 种风带来的干扰可以模拟四旋翼无人机在面对自然风时沿各个坐标轴方向所受的干扰量。以X轴为例：

假设基本风速a=2 m/s；渐变风于t0=2 s，t1=4 s，t2=6 s 时刻发生变化，渐变风最大风速为1.5 m/s；随机风的峰值速度为3 m/s，其具体仿真效果如图4所示。

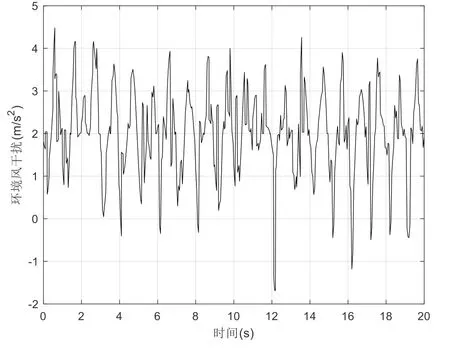
Fig.4 Interference of ambient wind on X-axis of quadrotor UAV图4 环境风对四旋翼无人机x轴的干扰

3 仿真实验与结果分析

对本文所提控制法与传统PID 控制法、反步自适应控制法进行性能比较。在MATLAB/Simulink 环境下分别搭建采用以上3 种控制器的四旋翼无人机系统模型，具体参数如表1 所示。通过仿真实验比较3 种控制策略在四旋翼无人机受到风场扰动时的控制效果。

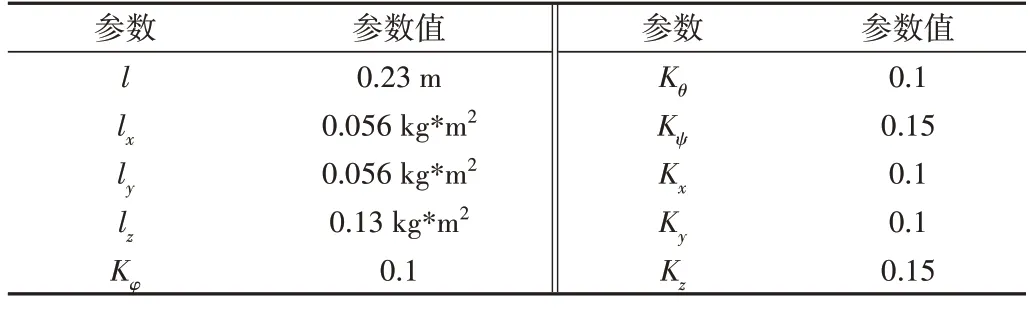
Table 1 Parameter settings of quadrotor UAV表1 四旋翼无人机参数设置

设定起始位置为地面坐标系E0的原点，各姿态角初始值均为0。参考文献［11］与文献［14］，再结合不断仿真调试优化，最终反步自适应分数阶PID 控制器的参数设置如表2 所示。作为对照的传统PID 控制器与反步自适应控制器参数设置参照文献［11］与文献［14］。

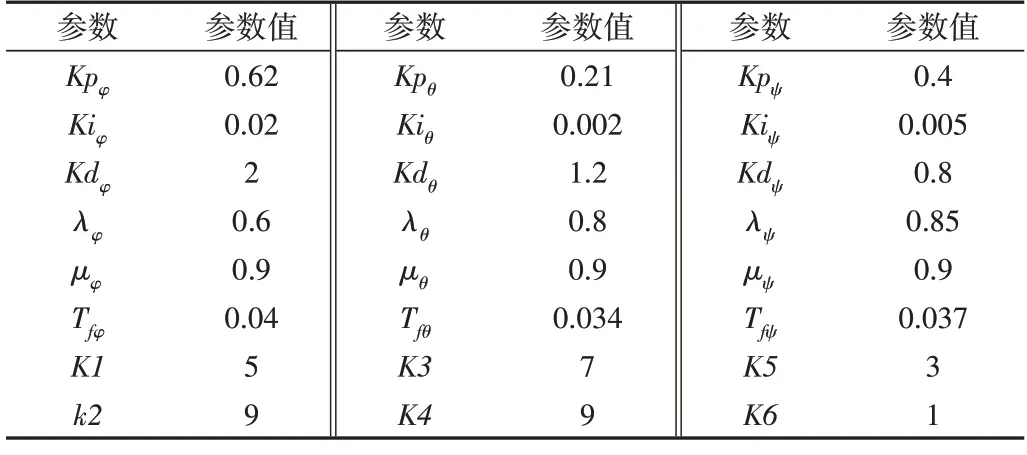
Table 2 Parameter settings of controller表2 控制器参数设置

设定四旋翼无人机预期位置为x=10 m，y=10 m，z=10 m，ψ=0.2 rad。首先忽略渐变风与随机风的影响，仅考虑基本风，则传统整数阶PID 控制器、反步自适应控制器以及本文设计的改进反步自适应分数阶PID 控制器对四旋翼无人机的控制效果如图5 所示。可以看出，传统整数阶PID 控制器在基本风干扰下虽然可以在有限时间内使飞行器达到预定值，但其调节时间较长且出现超调量，具有对外界干扰缺乏抵抗能力的缺点；反步自适应控制器与本文设计的反步自适应分数阶PID 控制器在该场景下均能有效抑制外界干扰，实现四旋翼无人机对预定轨迹的准确跟踪，但本文设计的控制算法所需调节时间更短、性能更佳。

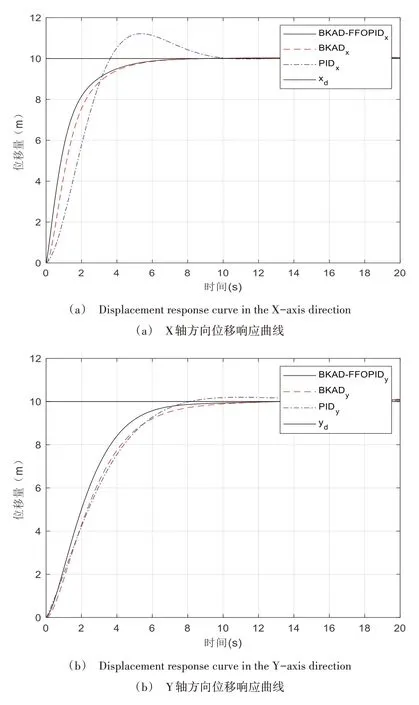
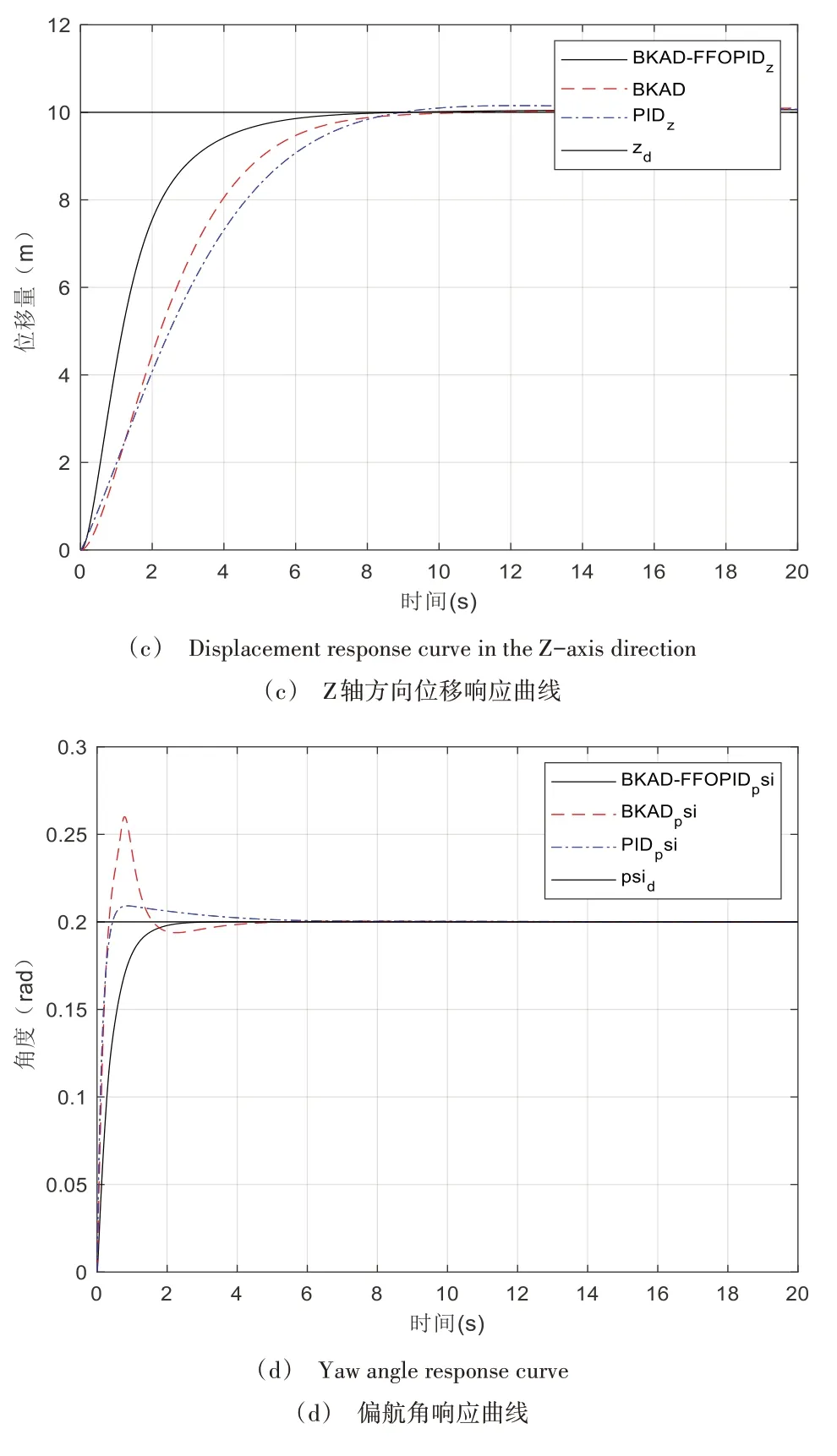
Fig.5 Control effect under basic wind图5 基本风下的控制效果

在复杂环境风干扰下进行仿真，PID、反步自适应以及本文设计的反步自适应分数阶PID 算法对四旋翼无人机的控制效果如图6所示。

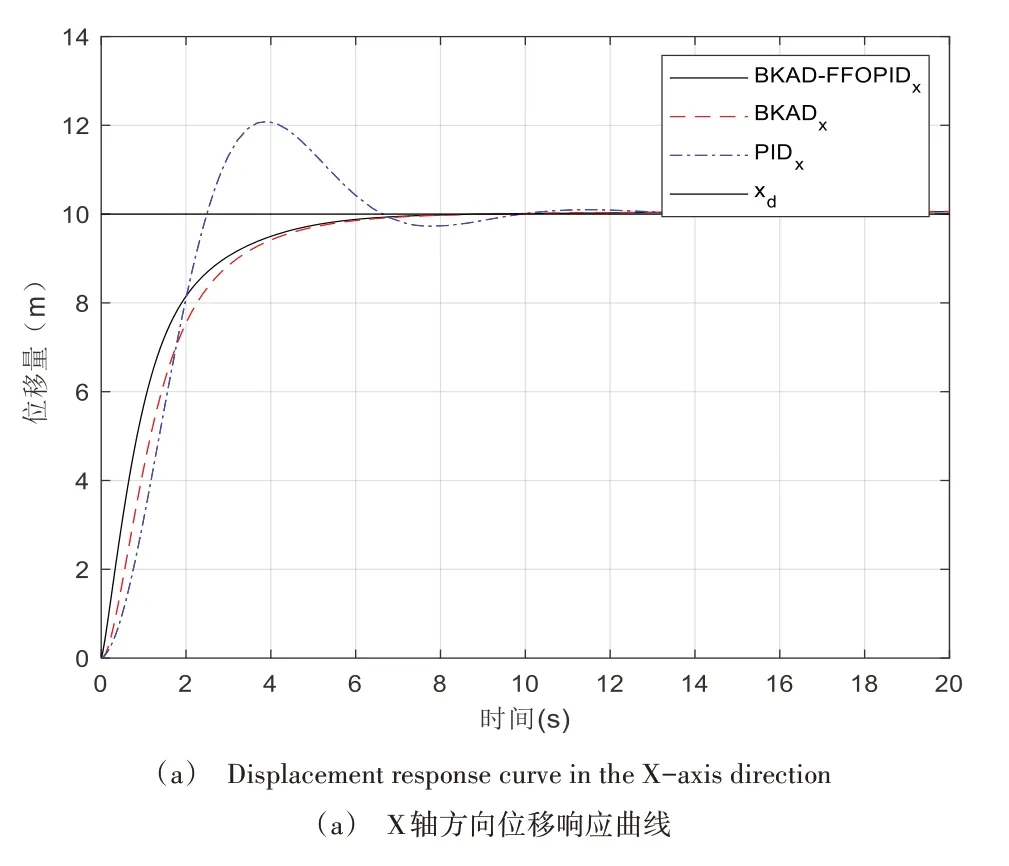
Fig.6 Control effect under complicated ambient wind图6 复杂环境风下的控制效果

可以看出，传统整数阶PID 控制在面对环境风之类复杂多变的干扰时控制效果进一步下降，所需调节时间更长的同时超调量波动也更大，反映了传统PID 控制易受外界干扰影响的缺点；反步自适应算法控制下的四旋翼无人机在环境风干扰下也能相对准确地追踪预定轨迹，但仍存在一定的稳态误差；本文设计的反步自适应分数阶PID 算法结合了上述两种算法的优点，在快速性、准确性、稳定性3个方面均优于传统PID 算法与反步自适应算法。

图7、图8、图9 分别展示了环境风干扰下本文控制算法、反步自适应算法、传统整数阶PID 算法的姿态控制效果。可以看出，传统整数阶PID 算法控制下的飞行器能基本响应姿态解算模块解得的预定姿态角，但当预定姿态角发生剧烈变化时控制器难以快速响应，从而影响无人机的实际轨迹，控制效果不理想；采用反步自适应算法的姿态变化曲线相较采用传统整数阶PID 算法更贴合预定变化曲线，且到达稳定状态用时更短，表明其响应速度与准确度均有所提高；采用本文算法控制的四旋翼无人机相较于反步自适应控制再次提高了跟踪精度且缩短了响应时间，即使预定姿态角发生剧烈变化也能及时调整。原因在于传统整数阶PID 控制是典型的线性控制器，面对复杂环境风的干扰下鲁棒性不足，超调量与调节时间远远超过其余两种控制器；反步自适应控制有效提高了系统的鲁棒性，降低了超调量，但在接近预期值时速度会显著降低；本文设计的反步自适应分数阶PID 控制保留了反步自适应控制的优点，加入改进后的分数阶PID 控制，通过低通滤波器减少高频扰动的干扰，同时引入前馈补偿提高了系统的跟踪性能，效率与准确率均有所提升。

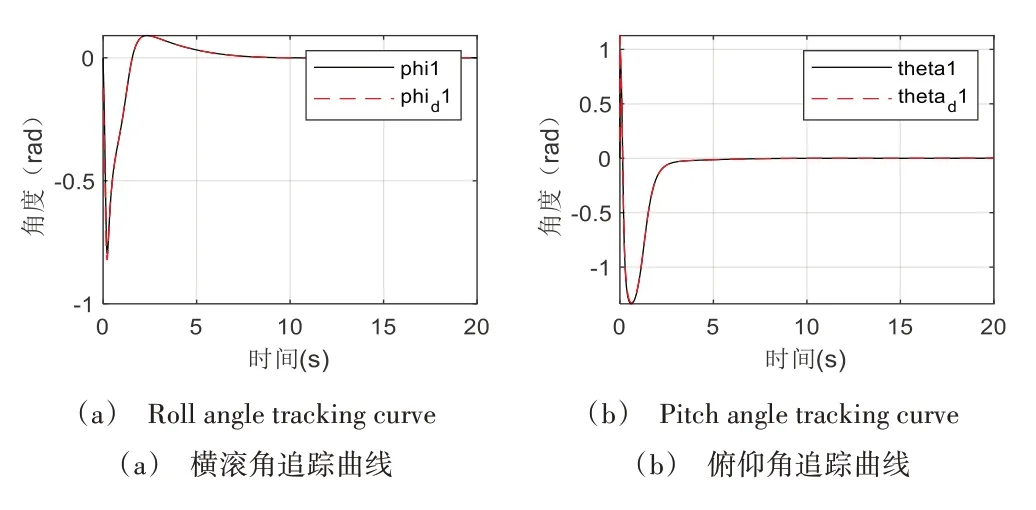
Fig.7 Attitude tracking results of the proposed controller图7 本文控制器姿态追踪结果

Fig.8 Attitude tracking results of backstep adaptive controller图8 反步自适应控制器姿态追踪结果

Fig.9 Attitude tracking results of traditional integer order PID control algorithm图9 传统整数阶PID控制器姿态追踪结果

根据仿真结果分别计算3 种控制策略的平方误差积分值（Square Error Integral，SEI），结果见表3。叠加不同算法各个坐标轴的SEI 值进行分析，可得本文控制器的SEI值较反步自适应控制器降低约27%，较传统PID 控制器降低约53%，证明改进后的反步自适应分数阶PID 控制法可使四旋翼无人机快速、平稳地抵达预期位置。

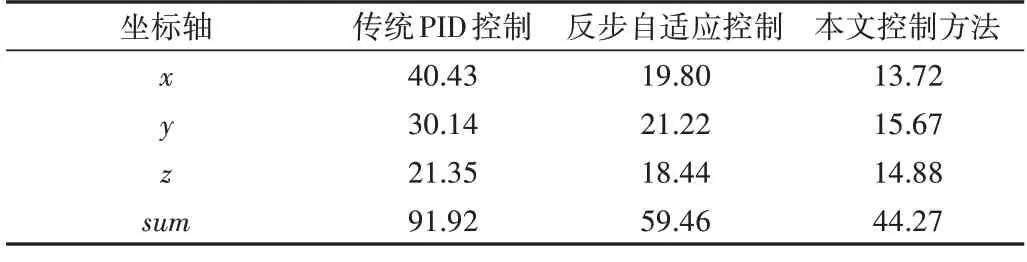
Table 3 SEI values of 3 control strategies表3 3种控制策略的SEI值

4 结语

本文对四旋翼无人机的飞行原理以及模型进行分析，以反步控制理论、自适应控制理论、PID 控制理论为基础提出一种对四旋翼无人机内外环分别采用反步自适应控制、改进分数阶PID 控制的策略，并通过仿真实验证实了改进控制策略对无人机姿态的追踪性能突出，具有鲁棒性强、响应速度快、准确性高等优点。然而本文提出的控制策略仍存在以下待改进之处：①忽略了陀螺效应对四旋翼无人机的影响，虽然降低了建模复杂度，但也因此使无人机的建模状态与实际工作状态产生偏差，未来需要考虑陀螺效应；②参数整定更多依赖经验，无法最优化算法性能，未来可通过神经网络等智能手段获取更优秀的参数；③理想适用范围存在局限，可考虑引入动态调节的特性扩大该控制算法的理想适用范围。