基于MIMU的输电杆塔螺栓状态识别

陶 慧, 贺国帅, 杨金显, 艾朋伟

(1.河南理工大学 电气工程与自动化学院, 河南 焦作 454003; 2.河南省智能装备直驱技术与控制国际联合实验室,河南 焦作 454003)

电力输电杆塔各部件常用螺栓连接,在长期风荷载影响下,螺栓连接点会发生松动,严重的松动会引起杆塔的倒塌。因此对输电杆塔螺栓进行状态识别,具有一定的研究意义[1-2]。

常用的螺栓松动检测方法有传统力矩法、压电阻抗法、图像法和振动分析法等[3-4]。传统力矩法是运维人员通过力矩扳手测量螺栓预紧力来判断螺栓是否发生松动,由于杆塔螺栓众多,检测效率较低。压电阻抗法通过对比螺栓松动前后的电阻抗来判断螺栓状态是否变化[5-6],由于压电阻抗检测设备昂贵,该方法在输电杆塔上应用受到了一定的限制。图像法对螺栓点蚀、剥落等外型损伤检测效果明显,但对于螺栓内部出现断裂和预紧力不足导致松动等故障并不适用[7-8]。振动分析法是对螺栓松动前后的振动信号必要处理,识别螺栓状态,且振动信号获取较为容易,设备成本低,适用于输电杆塔螺栓状态识别。何冰等[9]通过比较螺栓松动前后振动信号频域幅值变化来判断螺栓是否发生松动。Ji等[10]对杆塔振动信号建立风振垂直应变响应均方根差识别指标,对输电杆塔塔腿构件螺栓松动位置进行识别。Zhao等[11]提出了一种利用振动信号固有频率和径向基神经网络识别螺栓松动位置和严重程度的方法。Tan等[12]利用小波包对振动信号分析结合神经网络对输电塔松动螺栓进行识别。以上研究均使用单轴加速度传感器测量杆塔螺栓一维振动信号,对螺栓松动进行识别。相比于单轴加速度传感器,微惯性测量组合(micro inertial measurement unit,MIMU)集成3个MEMS加速度计和3个MEMS陀螺仪,测量杆塔螺栓三轴加速度和三轴角速度振动信号,可以更好地反应螺栓松动前后的状态,并且具有体积小、功耗低和成本低等优点[13],本文采用MIMU测量输电杆塔螺栓松动前后6维振动信号。

杆塔螺栓的状态识别主要是对振动信号进行分析,一般采用时域频域分析法,杆塔螺栓松动后,连接结构之间发生共振,出现非线性响应,可以利用螺栓松动前后6维响应信号的时域频域特征进行螺栓松动识别[14-15]。熵权法(entropy weight method,EWM)依据原始数据提取的方差、峰-峰值、峭度、频率方差、重心频率和能量特征,客观反应所提取特征的权重[16-17]。KL(Kullback Leibler)散度能够衡量两个概率分布之间的差异,KL散度值越小,分布越接近[18]。当杆塔螺栓松动时,相应的敏感特征及其权重也会发生变化,将特征权重作为概率空间的概率分布,构建特征权重分布,结合KL散度可以对输电杆塔螺栓状态识别。

本文提出一种基于MIMU的输电杆塔螺栓状态识别的方法。首先搭建输电杆塔模型,利用MIMU采集螺栓不同状态下的三轴加速度和三轴角速度原始振动数据,对原始数据降噪处理,提取降噪后振动数据敏感特征,根据熵权法计算敏感特征的权重构建特征权重分布,结合KL散度对输电杆塔螺栓状态进行识别。

1 数据采集与预处理

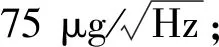
图1 输电杆塔螺栓振动数据模拟采集系统

将MIMU采集的三轴加速度和三轴角速度原始数据表示为

X={x1,x2,x3,x4,x5,x6}

(1)

式中:x1,x2,x3为三轴加速度;x4,x5,x6为三轴角速度;xi={xi1,xi2,…,xij,…,xin}T,i=1,2,3,4,5,6,n为序列长度。

因测量环境、传输路径和噪声的干扰,采集的6维惯性数据中存在随机噪声,为精确提取输电杆塔螺栓松动敏感特征,对振动数据进行降噪处理。最简单的数字滤波方法是中值滤波和均值滤波,五点三次平滑法相较于中值滤波和均值滤波,在一定程度上可减小信号中的高频随机噪声,有效处理传感器在工作中产生的低频周期信号和随机干扰信号所引起的尖峰、毛刺现象,且计算简单方便[19],本文使用五点三次平滑法对6维振动信号进行降噪处理,计算公式为

(2)

式中:yij为降噪后数据;xij为原始数据;yi={yi1,yi2,…,yij,…,yin}T,i=1,2,3,4,5,6,n为序列长度。

对试验采集的其中一组螺栓松动6维数据进行五点三次平滑滤波,得到的结果如图2所示。由图2可以看出,6维振动数据降噪处理后,没有尖峰毛刺等现象,波形更加平滑。其他采集的数据使用同样的方法处理,也可以得到较好的效果,这里不再给出。

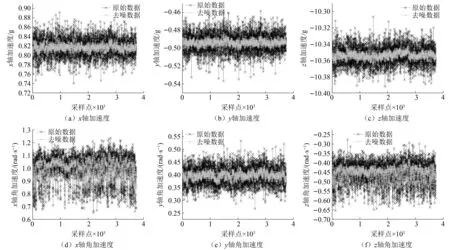
图2 模拟系统杆塔螺栓松动状态降噪结果

为了说明五点三次平滑法的效果,将其与其他常用振动信号降噪方法对比。常用的振动信号降噪方法除中值滤波和均值滤波等数字滤波外,还有小波阈值(wavelet threshold,WT)降噪和Kalman滤波降噪。这里选用db4小波对振动信号5层分解软阈值函数降噪处理;设定Kalman滤波初始参数为P=0.1,Q=0.1,R=1。由于实际测试中无法得到完全不含噪声的振动信号,无法利用信噪比(signal noise ratio,SNR)和均方误差(root mean squared error,RMSE)评价降噪效果,这里使用噪声抑制比(noise rejection ratio,NNR)来评估振动数据的降噪效果,NNR越大,噪声抑制效果越明显[20]。对采集的10组螺栓松动状态数据采用不同的降噪方法处理,得到的NNR平均值如表1所示。

表1 不同降噪方法的NNR

由表1可以看出:中值滤波和均值滤波噪声抑制效果相当,Kalman滤波噪声抑制效果最差,WT降噪相较于中值滤波、均值滤波和Kalman滤波噪声抑制效果有明显的改善,本文方法噪声抑制效果最明显。因为WT降噪存在阈值、小波基函数和分解尺度等参数选择困难的问题,且依赖噪声统计特性;Kalman滤波降噪适用于噪声特性已知的场合,由于外界环境的干扰使MIMU测量的振动信号噪声较为复杂,具有不确定性,依赖噪声统计特性的WT降噪和Kalman滤波方法,对螺栓振动数据处理难以取得理想的降噪效果。

2 振动信号敏感特征提取及权重计算

2.1 振动信号敏感特征提取

螺栓状态识别需要先提取输电杆塔螺栓振动信号的时域和频域等敏感特征。时域特征中,方差描述振动信号偏离中心的强度,峰-峰值描述振动信号变化的范围,峭度指标对振动信号中的冲击分量敏感;频域特征中,频率方差表示振动信号频率变化强度,重心频率反映振动信号频率的主频位置;当输电杆塔螺栓未松动时,振动信号能量分布较为均匀,当螺栓松动时,在外界激励的作用下,螺栓与连接物之间的局部刚度发生变化,使振动信号能量分布发生变化,能量也可以作为螺栓松动识别的敏感特征。提取降噪后振动信号的方差、峰-峰值、峭度、频率方差、重心频率和能量6个敏感特征。各特征定义如下:

(1)方差σ2

(3)

(2)峰-峰值F

Fi=max(yi)-min(yi)

(4)

(3)峭度Ku

(5)

(4)重心频率FC

(6)

式中:fij为yij傅里叶变换后的频率;sij为对应的幅值。

(5)频率方差VF

(7)

(6)能量E

(8)

分别计算降噪后一组螺栓正常状态和螺栓松动状态数据的σ2,F,Ku,FC,VF和E,得到的结果如表2所示。

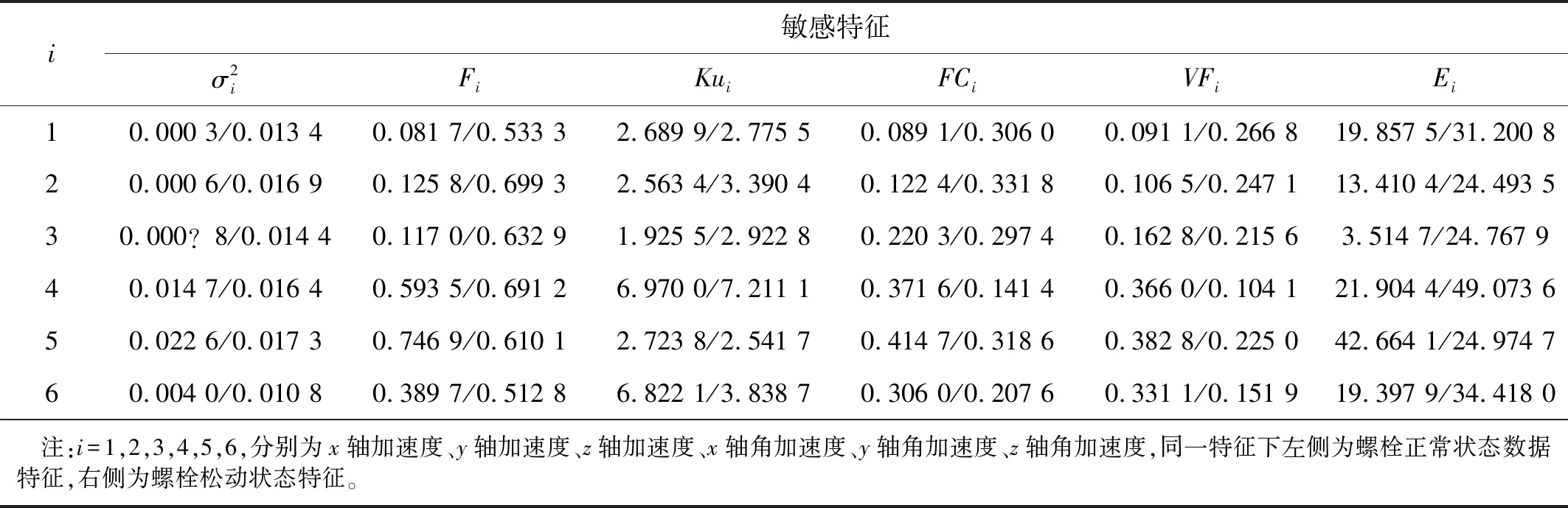
表2 杆塔螺栓正常和松动振动信号敏感特征

由表2可以看出,螺栓正常状态和松动状态的6维数据敏感特征之间的差异没有明显规律可循,直接使用提取的敏感特征难以识别螺栓状态,且数据维度较大。

2.2 熵权法求敏感特征权重

熵权法综合评价敏感特征的离散程度,熵值越小,对应的权重越大,由于测量信号的非平稳定性,避免主观性因素的干扰,采用熵权法对提取的振动信号敏感特征进行权重计算。

熵权法计算权重步骤如下:

步骤1建立特征矩阵B

(9)

式中,Ai,j为MIMU测量的第i维信号的第j个特征,i=1,2,3,4,5,6,,j=1,2,3,4,5,6。

步骤2数据归一化。根据max-min法对特征矩阵B归一化处理。

(10)

式中:max(Aj)为所提取的第j个特征的最大值;min(Aj)为所提取第j个特征的最小值。

步骤3计算特征所占的比重Pij

(11)

步骤4计算第j个特征的熵值Hj

(12)

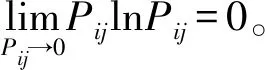
步骤5计算第j个特征的权重wj

(13)

利用熵权法对表2提取的敏感特征求权重,结果如表3所示。

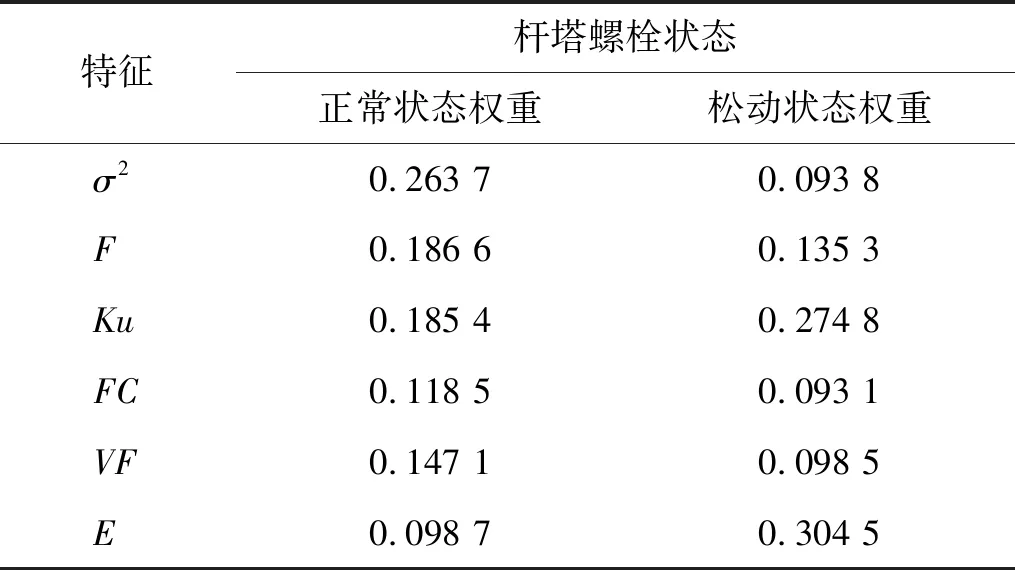
表3 杆塔螺栓正常和松动敏感特征对应的权重

由表3可以看出,经熵权法处理后,数据的维度减小,杆塔螺栓不同状态提取的特征权重不同。将提取的6个敏感特征的权重记为W=(w1,w2,w3,w4,w5,w6),为螺栓状态识别做准备。

对试验采集的20组数据降噪处理,计算6个敏感特征,建立特征矩阵B,依据熵权法计算敏感特征的权重W,20组数据的特征权重如图3所示。图3中:1～10组为螺栓正常状态数据;11～20组为螺栓松动状态数据。

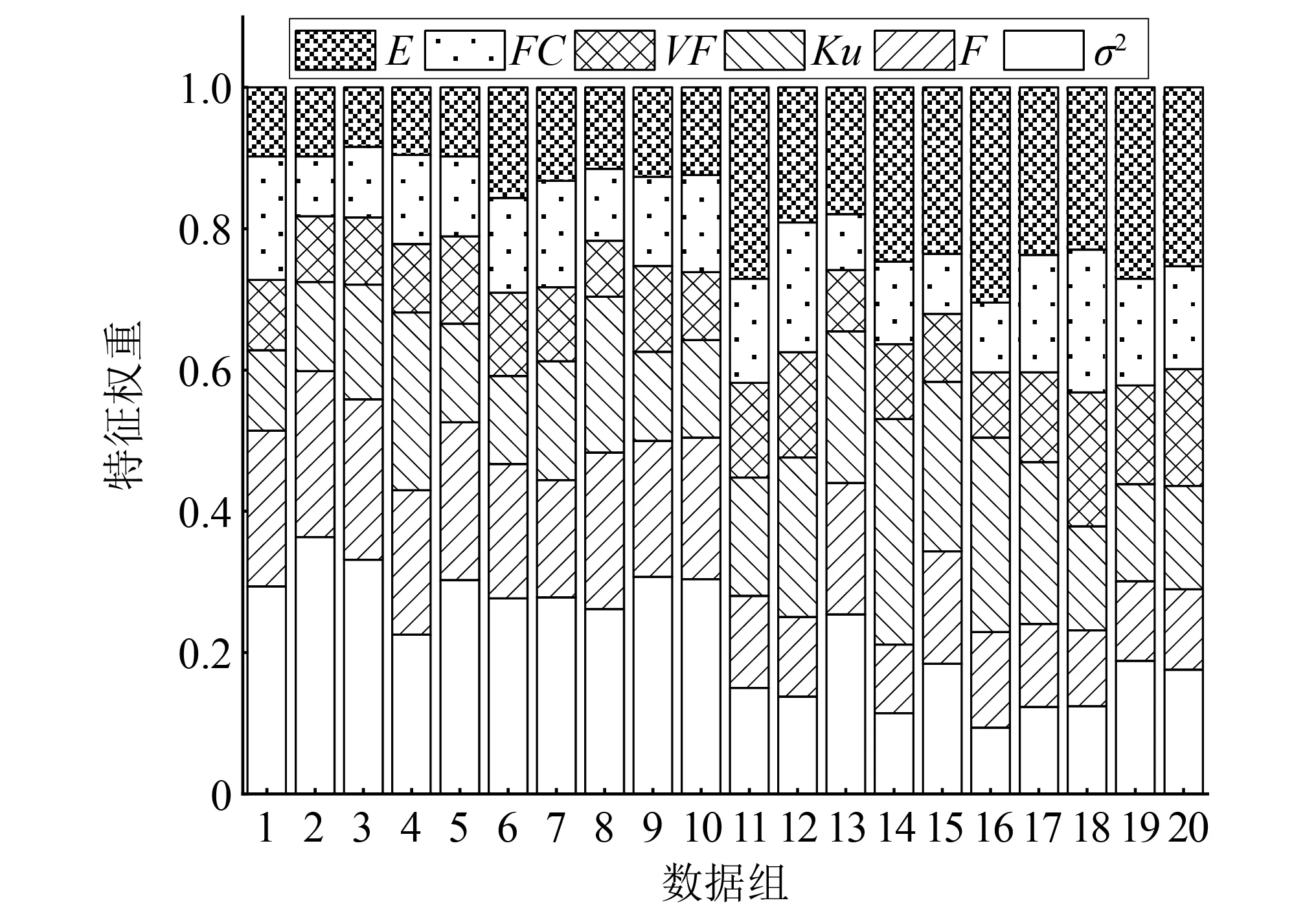
图3 模拟杆塔螺栓不同状态特征权重

由图3可以看出,螺栓相同状态数据组之间的特征权重值大致相同,螺栓不同状态数据组之间的特征权重值有一定差异。对比螺栓松动前后各敏感特征权重变化,可以得出,当杆塔螺栓松动时,σ2的权重变化趋势为明显减小,E的权重变化趋势为明显增大,F,Ku,FC和VF的权重有一定变化,但整体变化趋势不明显。

3 基于KL散度的螺栓松动识别

3.1 KL散度

KL散度用来衡量两个分布之间的差异,将特征权重作为概率空间的概率分布,构建特征权重分布,螺栓状态不同,特征权重分布不同,计算杆塔螺栓不同状态特征权重分布之间的KL散度值,对螺栓状态识别。KL散度值越小,说明特征权重分布越接近,即杆塔螺栓状态越相似。

KL散度计算公式为

(14)

式中,WⅠ(wj),WⅡ(wj)为杆塔螺栓不同状态特征权重分布。

3.2 模拟杆塔螺栓松动识别

重新采集一组螺栓正常状态数据和螺栓松动状态数据,降噪处理后,依据熵权法计算新采集数据的特征权重,构建特征权重分布,根据式(14),分别计算新采集数据的特征权重分布与图3中已采集的20组数据的特征权重分布之间的KL散度值,结果如图4所示。

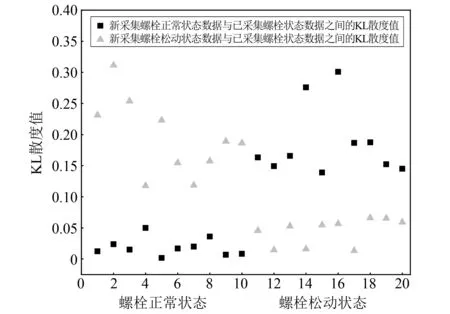
图4 模拟杆塔数据特征权重分布KL散度值

由图4可以看出:新采集的螺栓正常状态数据与已采集的螺栓正常状态数据之间的KL散度值较小,与已采集的螺栓松动状态数据之间的KL散度值较大,且有明显的区分;新采集螺栓松动状态数据与已采集的螺栓正常状态数据之间的KL散度值较大,与已采集的螺栓松动数据之间的KL散度值较小,且有明显区分,螺栓状态可以有效识别。因此可以通过比较新采集杆塔螺栓数据的特征权重分布与杆塔螺栓历史数据特征权重分布之间的KL散度值,来判断新采集的杆塔螺栓的状态,即杆塔螺栓是否松动。

3.3 实测杆塔螺栓松动识别

将N100WP型MIMU和手持风速仪固定在距离被测螺栓10 cm处,用光纤把MIMU模块和PC上位机数据采集系统连接,在自然风情况下,采集某户外正在使用的110 kV酒杯型,如图5(a)所示,输电杆塔塔底螺栓的6维振动数据。实测数据采集系统如图5(b)所示。杆塔螺栓正常状态如图5(c)所示,由于杆塔长期处于户外工作,在风吹雨淋后,会对螺栓有一定的腐蚀及风化,使螺栓预紧力降低,在风振作用下造成螺栓松动,杆塔螺栓松动状态如图5(d)所示。

图5 杆塔螺栓振动数据采集系统

根据实测的杆塔螺栓振动数据采集系统,手持风速仪测得瞬时风速17 m/s,采集10组杆塔螺栓正常状态数据和10组螺栓松动状态数据,每组采样点为3 500,采样时间为10 s。对采集的20组振动数据采用和模拟试验数据同样的方法处理,得到的敏感特征权重如图6所示。图6中:1～10组为螺栓正常状态数据;11～20组为螺栓松动状态。

图6 实测杆塔螺栓不同状态特征权重

由图6可以看出:10组螺栓正常状态数据之间的特征权重分布相似,10组螺栓松动状态数据之间特征权重分布相似;螺栓正常状态与螺栓松动状态之间的特征权重分布差异较大。当螺栓松动时,σ2的权重明显减小,E的权重明显增大,其余特征的权重变化趋势不明显,与模拟输电杆塔试验得出的结论一致。

重新采集一组现场螺栓正常状态数据和一组螺栓松动状态数据,对数据使用本文方法处理,分别计算新采集数据的特征权重分布与图6中的20组数据的特征权重分布之间的KL散度值,结果如图7所示:

图7 实测杆塔数据特征权重分布KL散度值

由图7可以看出:新采集的螺栓松动数据与10组螺栓正常数据的KL散度值较大,与10组螺栓松动数据之间的KL散度值较小;新采集的螺栓正常状态数据与10组螺栓松动数据之间的KL散度值较大,与10组螺栓正常状态数据之间的KL散度值较小,且有明显区分,可以对输电杆塔螺栓的状态进行有效识别。

4 结 论

本文利用MIMU采集杆塔螺栓6维原始振动数据,采用五点三次平滑法对数据进行降噪,利用熵权法计算降噪后6维数据的时域、频域和能量特征权重,将特征权重分布结合KL散度法对螺栓状态进行识别。

(1)利用熵权法对降噪后数据计算方差、峰-峰值、峭度、频率方差、重心频率和能量特征权重,从数据结果分析得出,当杆塔螺栓松动时方差的权重减小,能量的权重增大,螺栓不同状态的特征权重分布不同。

(2)模拟杆塔螺栓试验数据和实测现场螺栓数据处理的结果表明,将特征权重分布与KL散度结合可以对螺栓状态进行有效识别。