颗粒流变破碎与堆石料流变应变计算

迟世春，郭 宇，马锡钰，贾宇峰

(大连理工大学建设工程学部工程抗震研究所，辽宁 大连 116024)

1 问题的提出

堆石坝的观测资料显示，坝体竣工后发生的流变变形可持续几年、十几年甚至更长[1]。通常在建坝蓄水后一年可完成总流变的75%，到第二年可完成总流变的95%[2]。如1971年1月竣工澳大利亚110 m高的塞沙那(Cethana)面板堆石坝，1973年～1980年间，坝体沉降和水平位移分别以每年4 mm和3 mm的速率发展，至1980年11月坝顶最大沉降达64 mm、最大水平位移达44 mm。我国95 m高的西北口面板坝，观测竣工时最大沉降为36 cm，8年后沉降发展至66 cm。天生桥面板堆石坝建成蓄水多年，坝体最大沉降达到3.47 m，沉降坝高比为2.24%。后来建成的洪家渡、三板溪以及水布垭面板堆石坝沉降与坝高之比分别达到了0.74%、0.84%、1%[3]。堆石坝运行多年后，变形仍不稳定并持续发展是一种常见现象。流变变形还影响堆石坝施工进度安排。堆石料施工后一般需要设置预沉降时间，如面板坝堆石体填筑完成后至面板浇筑前堆石体需要的静置时间，以满足后续结构对前期堆石体变形的要求，这显然影响工程建设周期。

堆石料这种竣工后发生的流变变形，恶化了防渗面板与心墙的应力变形状态，导致面板发生脱空、裂缝、挤碎及止水破坏，心墙堆石坝则发生坝体表面裂缝、心墙内部水力劈裂等，影响大坝防渗安全，增加运维费用并影响工程效益的发挥。

堆石料流变研究目前多采用三轴流变试验方法。沈珠江[4]进行了不同围压与应力水平下的单级加载流变试验，基于Merchant模型提出了堆石料流变的三参数模型，在分离了时间因素后，给出了最终流变量的计算表达式，认为剪切流变仅与应力水平有关，体积流变与围压成正比。李国英等[5]通过对公伯峡堆石料试验，修正最终体积流变为围压和广义剪应力的函数，流变参数增加至6个。程展林等[6]开展了水布垭主堆石料的流变试验研究，提出了堆石料九参数流变模型的数学表达式及相应的参数指标，认为堆石料流变随时间增长为幂函数关系。李海芳等[7]通过九甸峡面板坝堆石料的流变试验，建议采用对数函数描述轴向流变的时间过程，采用指数函数描述体积流变的时间过程。王海俊和殷宗泽[8]对两种不同岩性的堆石料进行了室内常规三轴流变试验，发现堆石料的体积流变和剪切流变随时间均呈现双曲线变化规律，提出了双屈服面流变模型。还有许多学者开展了堆石料的流变试验，包括侧限压缩流变试验和三轴流变试验。这些研究极大地丰富了堆石料室内流变试验的成果，证实了堆石料普遍存在流变特性的事实。但这些流变公式均为试验曲线的拟合，属于经验类模型。

堆石料流变试验最大的难题是设备占用时间长。堆石坝一般由多种坝料组成，上坝堆石料控制级配范围多样。堆石料的碾压指标为孔隙率，碾压后的实际干密度一般在一定范围内变化。因流变计算多采用插值方法，一组试验一般需要进行3个围压、3个应力水平的流变试验，而每个试样的三轴流变试验需要一周以上的时间。因此，流变试验工况覆盖坝料种类、级配、密度的变化以及满足插值方法要求是比较困难的，绝大多数情况下采用简化工况，只进行代表性工况试验，故寻求更简便的流变试验方法是必要的。

流变试验的第2个问题则是稳定竖向荷载与围压。流变试验大多是在应力控制式三轴试验仪上进行，由于试样持续的流变变形，为维持恒定的应力条件，竖向荷载一直处于不断调整的波动状态，竖向加载轴不断进出压力室，也将引起围压调整，特别是每个试验持续时间长，对试验设备特别是竖向荷载的伺服系统要求高。

流变试验的第3个问题是流变的起算时间。整理流变试验结果时，首先需要将试验中的流变变形与瞬时变形分开。但目前工程学术界对于流变变形的起算时间还没有形成共识。李海芳等[7]建议将1 h作为应力加载瞬时变形与流变变形的分界点；程展林等[6]则建议采用2 h作为分界点；朱晟等[9]建议采用0.75 h作为流变变形的起算时间。图1为试验得到的流变应变与时间对数的关系。从图1可以看出，即使试样加载1 h内的变形不作为流变变形，其后1 h的流变应变可达0.08%～3%左右，约占总流变应变的30%～80%。因流变试验的前期变形占比很大，流变变形速率衰减很快，故流变应变的起算时间直接影响流变应变的量值与衰减规律。

图1 堆石料蠕变[7]

2 颗粒破碎与堆石料变形

堆石料经碾压密实，已经形成紧密的颗粒骨架结构。若只承受体积应力，在工程围压范围内堆石料不发生变形、颗粒亦不破碎，这已被三轴试验固结阶段的结果所证实。若在低围压承受剪应力，围压不足以约束颗粒间的翻越，在剪应力的作用下颗粒之间相互滑移、翻越及结构调整，进而引起堆石原有结构的丧失。实际工程中几乎见不到坝体表面自然条件发生结构性丧失的情况，说明堆石坝中低围压下剪胀变形即使有其占比也非常有限。当围压达到一定数值后，堆石料再受剪切作用，堆石料变形则由颗粒破碎引起的颗粒间填充、滑移、错动等造成。这种变形以剪切变形为主，并伴随颗粒破碎引起的体积收缩，即“剪缩”，从而出现面板堆石坝浇筑面板前上游堆石料发生的亏坡，浇筑的前期面板发生脱空等现象。因此堆石料变形与颗粒破碎密切相关。

颗粒破碎与堆石料变形的关系，贾宇峰等[10]曾进行过系列三轴试验，认为堆石料剪切过程中颗粒破碎参量与轴向应变为双曲线表达式，且试样轴向应变随颗粒破碎的增加而单调增大；吴二鲁等[11]给出了破碎指标、围压及轴向应变之间的关系式，由于三轴试验中围压固定，颗粒破碎与轴向应变的关系式也是唯一确定的；刘萌成等[12]给出了三轴试验中破碎参量与体积应力及偏斜应力的表达式，在围压固定的条件下偏斜应力与轴向应变以及体积应变与轴向应变的关系曲线由静力三轴试验唯一确定，因此其破碎参量与应变的关系也是确定的；石北啸等[13]的三轴试验表明，堆石料破坏剪胀率与颗粒破碎率具有单调关系；王启云等[14]还研究动力循环荷载作用下粗粒土填料的累积应变与颗粒破碎的关系，显示颗粒破碎与累计应变的对数成线性关系。因此，堆石料变形与颗粒破碎具有强对应关系，可以通过颗粒破碎来预测堆石料变形，包括静力瞬时变形、流变、湿化变形、动力变形等。

堆石料静力瞬时变形与颗粒受力后的瞬时破碎有关，流变变形则与颗粒的流变破碎有关。堆石颗粒的流变破碎指的是堆石料颗粒受力小于瞬时强度，不会发生瞬时破碎；但大于颗粒长期强度，在颗粒长期受力过程的某个时间点上发生破碎，进而引起堆石体流变变形。破碎时间取决于颗粒内部缺陷与受力状态。

3 堆石颗粒的长期强度

3.1 单颗粒蠕变仪确定长期强度

大连理工大学研制的单粒岩块蠕变试验仪结构示意如图2所示。其试验原理为：颗粒在试验中受到上、下平行的刚性平板挤压；利用砝码和双杠杆机构对颗粒施加长期稳定的竖向荷载，最大竖向力40 kN；手轮和丝杠可以调节杠杆平衡以保证荷载按照预定放大系数传递；横梁、调节杆、辅助杆、导向杆和定位柱共同组成具有防偏功能的荷载传导装置；利用高精度的位移传感器可以自动测定并记录颗粒在恒定荷载作用下的变形量。

图2 岩块颗粒蠕变试验装置示意

试验采用分级加载方式，每级荷载持续7 d后施加下一级荷载；分两种情况进行试验，第I类颗粒在经历一到二级恒载作用后，如果没有出现蠕变破碎现象便通过增加砝码使其发生破坏，计算颗粒瞬时强度σc；第II类颗粒在经历若干级恒载作用后出现蠕变破碎现象，即在某一恒载作用下在不足7 d的某一时刻突然发生整体劈裂破碎。位移传感器每1 h自动记录一次数据。颗粒应力指标为

(1)

式中，F为颗粒所受荷载；d为颗粒粒径。

两类颗粒试验工况分别见表1和表2。

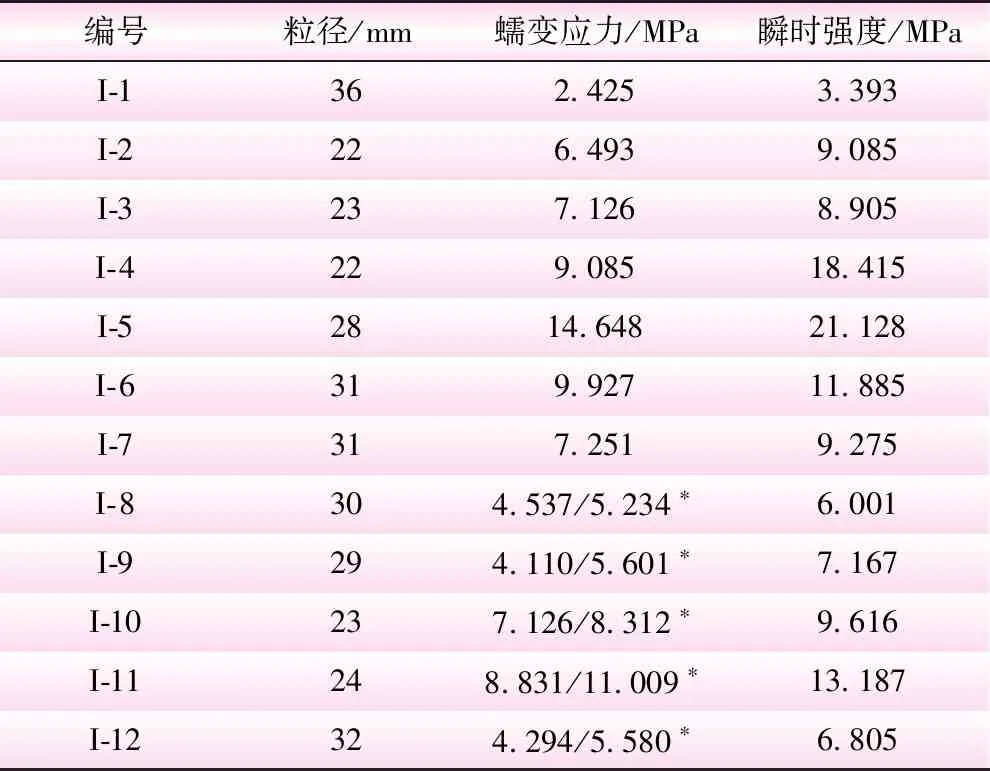
表1 第I类颗粒试验工况

表2 第II类颗粒试验工况

第I、II类颗粒蠕变曲线分别见图3、4。从图3、4可以看出，应力施加后会产生较大的瞬时应变。在恒定应力作用下应变会随时间的延长逐渐增大。当恒定应力较低时，应变会随着加载时间的无限延长而趋于某一定值；当恒定应力超过某值时，应变不再收敛，并发生蠕变破碎，蠕变破碎具有突然性。

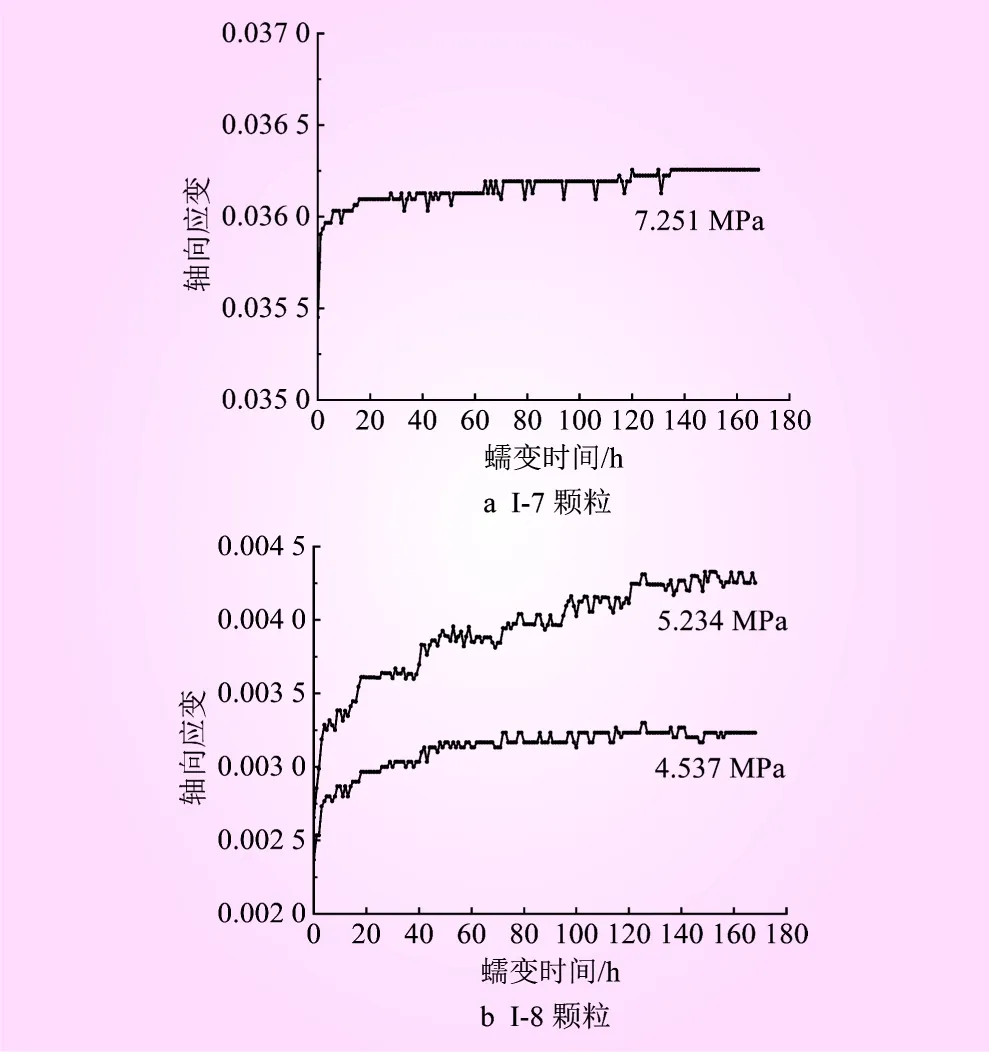
图3 第I类颗粒的蠕变曲线

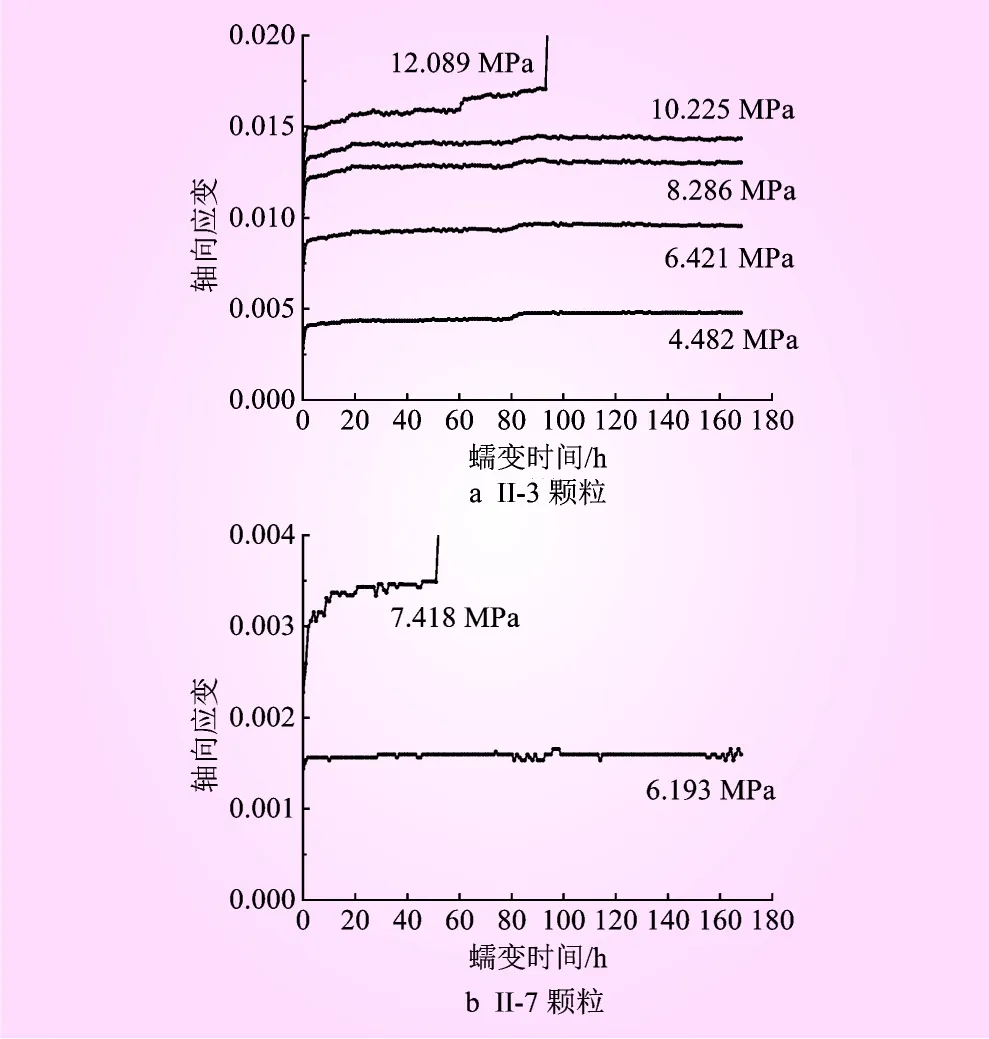
图4 第II类颗粒的蠕变曲线

颗粒长期强度指颗粒长期受力过程中破碎的最低应力。当颗粒受力大于等于瞬时强度时，颗粒会瞬时破碎；当颗粒受力不超过长期强度时，不破碎；当颗粒受力介于长期强度和长期瞬时之间时，颗粒发生蠕变破碎。确定长期强度多采用间接法，有等时曲线法和过渡蠕变法之分。根据第I类颗粒试验结果，研究应力水平和稳态蠕变速率之间的关系，估计颗粒的长期强度。稳态蠕变速率为各加载步最后3 d应变时间曲线的斜率。

定义长期强度与瞬时强度之比为长期强度应力水平S∞，当前应力与瞬时强度之比为应力水平S，即

式中，σ∞为颗粒长期强度；σc为颗粒瞬时强度；σ0为颗粒试验所受蠕变应力。

颗粒的稳态蠕变速率与应力水平的关系如图5所示。从图5可以看出，稳态蠕变速率在应力水平0.7～0.8之间存在一个临界点。在该点以左，稳态蠕变速率很小；在该点右侧，稳态蠕变速率徒增。为了确定该临界点，可取图5中应力水平小于0.7和大于0.8的部分分别进行线性拟合得到直线l1和l2，取两直线交点的横坐标为长期强度应力水平。试验得到的颗粒长期强度应力水平为S∞=77.12%。

图5 第I类颗粒试验中颗粒稳态蠕变速率与应力水平

3.2 断裂力学方法确定颗粒长期强度

格林菲斯理论认为，材料内部存在许多细微裂隙，在力的作用下，这些裂隙的周围，特别是缝端，会产生应力集中现象。材料的破坏从缝端开始，裂隙扩展，最后导致材料完全破坏。将材料中含有大量方向杂乱的微裂隙，概化一张开的椭圆形裂缝，采用格里菲斯强度公式进行计算。堆石颗粒内部存在着各种缺陷，概化为一币形裂纹，在承受挤压力被劈裂的过程中，裂纹尖端的应力强度因子为

(3)

式中，σθ为垂直加载轴的颗粒张拉劈裂应力；Y为形状因子(无量纲)，是a/R的函数；a为概化裂缝长度的1/2；R为粒径的1/2。

(4)

变换式(3)为σθ的表达式，并代入式(4)，得

(5)

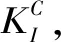
(6)

因此，长期强度应力比也可以通过测量颗粒岩石的起裂韧度与断裂韧度确定。

采用大连理工大学研制的岩石双扭试验仪量测颗粒岩石的起裂韧度与断裂韧度。首先，选择同一工程同一岩性粒径较大的颗粒若干，加工成双扭试件，试件受力见图6。试验中逐渐增大荷载，观测试样预裂。沿试件背面的沟槽预裂至新鲜裂纹出现，则根据预裂状态受力计算起裂韧度。然后固定加载位移进行松弛试验，测算亚临界裂纹扩展参数。最后增大荷载至裂纹贯穿并计算断裂韧度。

图6 岩石双扭试件及受载示意(L×W×d=150 mm×50 mm×4.8 mm)

双扭试验得到的颗粒岩石起裂韧度与断裂韧度见表3。计算起裂韧度与断裂韧度之比为长期强度应力水平，测量得到的长期强度应力水平平均值为0.78。与3.1节用常规方法确定的长期强度应力水平为0.771 2差别仅1.14%。由此也间接说明3.1节的方法确定的长期强度应力水平可行。

表3 颗粒岩石起裂韧度、断裂韧度及长期强度应力水平

4 堆石料流变应变与颗粒长期强度

4.1 堆石料流变模型

堆石料的流变模型采用分离变量法将时间项t分离出去，即

εc(t)=εf(1-e-αt)

(7)

式中，εf为最终流变应变量，可分为最终体积流变应变εvf和最终剪切流变应变εsf；α为衰减参数。最终流变应变是应力条件的函数，即[5]

(8)

式中，σ3为围压；Pa为一个大气压力；SL为应力水平；b、c、d、m1、m2、m3为试验参数。

4.2 堆石料最终流变应变和颗粒长期强度的关系

堆石体中的每个颗粒的受力状态有3种情况。一是受力形成的劈裂应力超过瞬时强度，这时的颗粒会立即破碎，形成瞬时变形，这就是通过常规三轴试验测量得到的变形；二是受力形成的劈裂应力小于瞬时强度但超过长期强度，这时的颗粒会在承受荷载后的某个时刻发生破碎，引起流变变形；三是受力形成的劈裂应力小于长期强度，这时的颗粒不会发生破碎。

实际上，三轴试验是在一定围压条件下通过连续增大轴向偏应力来实现对试样的宏观剪切作用的。这种情况下可以将施加的轴向偏应力看作无数个连续的极小荷载增量的累加。若三轴试验的加载速率越快，则每一个极小荷载增量的作用时间就越短。

首先考虑一种加载速率足够慢的三轴试验。在该试验中，每一个极小荷载增量的作用时间都将无限大。于是，在这种试验的一个极小荷载增量的作用时间内，一旦某个颗粒受力形成的劈裂应力超过长期强度，那么这个颗粒必然会发生破碎。虽然在漫长时间内，颗粒的破碎不会同步发生，颗粒的受力会因其他颗粒破碎引起的应力重分布而发生改变，但是只要新的受力形成的劈裂应力仍然超过长期强度就意味着这个颗粒依然存在发生破碎的可能。同时，因为假定极小荷载增量的作用时间无限大，所以原始颗粒或者新生颗粒都可能在这段时间内发生破碎。当所有颗粒都不符合上述那种发生破碎的受力条件时，就是已经充分破碎了。由于每一个极小荷载增量的作用都以颗粒的充分破碎而收尾，那么加载速率足够慢的三轴试验的全过程应力-应变-体变曲线自然就包括了瞬时变形和流变变形。

第二考虑常规三轴试验。该试验的每一个极小荷载增量的作用时间很短。除了因受力形成的劈裂应力大于瞬时强度而发生的与时间无关的破碎外，其他受力条件的颗粒没有足够时间发生破碎。也就是说，常规三轴试验中的每一个极小荷载增量的作用不以颗粒的充分破碎结束，而是在满足瞬时破碎受力条件的那些颗粒发生破碎之后就结束了。因此，常规三轴试验的全过程应力-应变-体变曲线自然只包括瞬时变形。

综合上述分析易知，对于同一围压条件下的加载速率足够慢的三轴试验和常规三轴试验的全过程应力-应变-体变曲线而言，在同一目标偏应力下，用前者的应变减去后者的应变即可得这一围压与目标偏应力下的最终流变变形，如图7所示，图中εaf对应最终轴向流变，εvf对应最终体积流变。

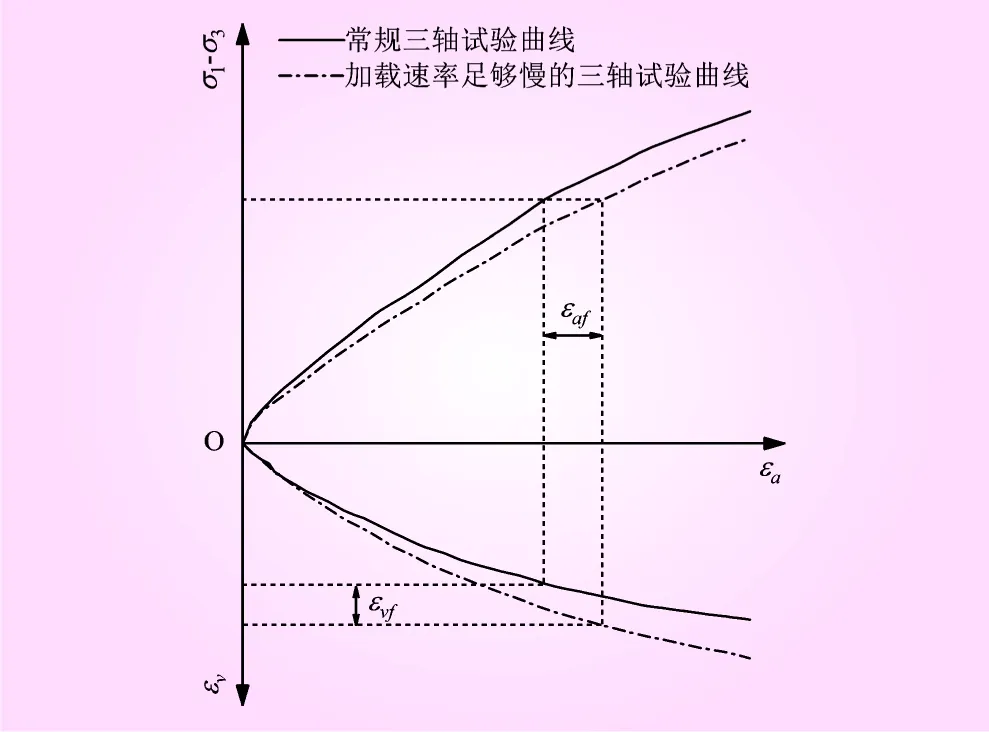
图7 加载速率足够慢的三轴试验曲线与常规三轴试验曲线

若有两个堆石料试样，从颗粒岩性到细观组构再到几何尺寸和颗粒级配等各方面均完全一致。一个试样进行常规三轴试验，试验过程中颗粒的破碎强度为瞬时强度；另一个试样进行加载速率足够慢的三轴试验，控制颗粒破碎的是长期强度。常规三轴试验中的试样中任一颗粒A，与加载速率足够慢的三轴试验中的颗粒B相对应。若两个试样破碎参量相同，即对应颗粒同时破碎或不破碎。颗粒A破碎时为瞬时强度σc，颗粒B破碎时为长期强度σ∞=S∞σc。要使颗粒A、B同时破碎，则颗粒A、B间的接触力满足

fst=S∞fct

(9)

式中，fst为加载速率足够慢的三轴试样内部颗粒接触力；fct为常规三轴试样内部颗粒接触力；S∞为颗粒长期强度应力水平。

三维状态下，颗粒集合体的等效应力和应变张量为

(10)

式中，Vσ为应力计算区域的总体积；f(c/p)为计算区域内颗粒q对颗粒p的接触力；l(c/p)为枝向量，是颗粒q指向颗粒p的向量；Vε为计算应变的区域对应的体积；Δue为构成边e的两个颗粒p和q中心的相对位移；de为边e对应的面积补偿向量。

由于两个试样的颗粒岩性、组构，级配等均相同，若两个试样内部颗粒具有相同的破碎状态时，其内部相应颗粒p对应的枝向量、计算区域体积、面积补偿向量以及内部颗粒相对位移均应相同，即

将式(9)和式(11)代入式(10)中，应力张量和应变张量满足如下关系式

=S∞σct

(12)

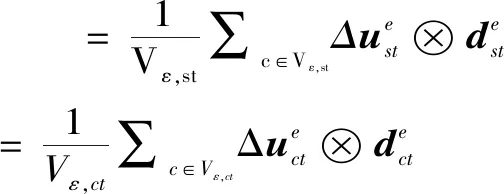
=εct

(13)

式中，σst和εst分别为加载速率足够慢三轴试样的宏观应力张量和应变张量；σct和εct分别为常规三轴试样的宏观应力张量和应变张量。

4.3 由常规三轴试验的应力应变曲线推求堆石料流变应变

为获取堆石料的变形参数，常进行堆石料饱和试样的常规三轴试验，得到应力-应变-体变关系曲线，并据此整理堆石料变形参数。

根据堆石料饱和试样的应力-应变-体变关系曲线，结合堆石颗粒的长期强度应力水平，可以推求加载速率足够慢三轴试样的应力-应变-体变关系曲线。颗粒岩性、组构、级配以及颗粒破碎完全相同的两个试样，其应力和应变张量满足式(14)、(15)，即

(σ3)st=S∞(σ3)ct，(σ1-σ3)st=S∞(σ1-σ3)ct

(14)

(εa)st=(εa)ct，(εv)st=(εv)ct

(15)

式中，(σ3)st、(σ1-σ3)st、(εa)st、(εv)st分别为加载速率足够慢三轴试样对应应力-应变曲线的围压、偏应力、轴向应变、体积应变；(σ3)ct、(σ1-σ3)ct、(εa)ct、(εv)ct分别为常规三轴试样对应应力-应变曲线的围压、偏应力、轴向应变、体积应变。

常规三轴试验与加载足够慢的三轴试验应力-应变曲线转换关系如图8所示。轴向流变应变与体积流变应变求取分3步。第1步利用颗粒长期强度应力水平将常规三轴试验的应力-应变-体变关系曲线，转换为加载速率足够慢三轴试验的应力-应变-体变关系曲线，对应图8中所示的①。转换过程中，偏应力-轴向应变曲线在应变相等的条件下偏应力降低为原来的S∞倍，同时曲线对应的围压也降低为原来的S∞倍。应变-体变曲线由于不涉及应力状态，而两种试样的应变张量相等，故曲线没有变动，但该曲线对应的围压降低为原来的S∞倍。第2步为加载速率足够慢的三轴试验曲线关于围压的插值，目的是换算成与原围压相等条件下包含流变应变的应力-应变-体变曲线，对应图8中所示的②。这样就得到了与常规三轴试验围压相同的加载速率足够慢的三轴试验的应力-应变-体变曲线。第3步，比较围压相同时常规与加载速率足够慢的三轴试验的偏应力-轴应变曲线，在同一目标偏应力下两者的差别即为轴向流变应变，见图8中的εaf；根据轴应变-体变曲线查轴向应变对应点的体积应变，两个对应点体积应变差就是流变体积应变，见图8中的εvf。

图8 常规三轴试验与加载足够慢的三轴试验应力-应变曲线转换关系

5 算 例

堆石料常规三轴试验曲线见图9中的瞬时曲线。为求取堆石料的最终流变量，采用颗粒长期强度与瞬时强度的比值，求出“颗粒长期强度”对应的加载速率足够慢的三轴试验曲线，包含最终流变应变的应力-应变-体变曲线，见图9中的长期曲线。由图9可以看出，应力-应变关系中颗粒破碎采用长期强度的曲线位于瞬时强度对应的常规三轴试验曲线的右侧。根据上节的方法，在同一偏应力下的差值就是流变轴向应变，由流变轴向应变在图9b中查对应点可确定流变体积应变。如此，可确定不同围压及应力水平下的流变应变。堆石料最终流变应变的计算值如图10所示，4个应力水平的最终流变应变见表4。

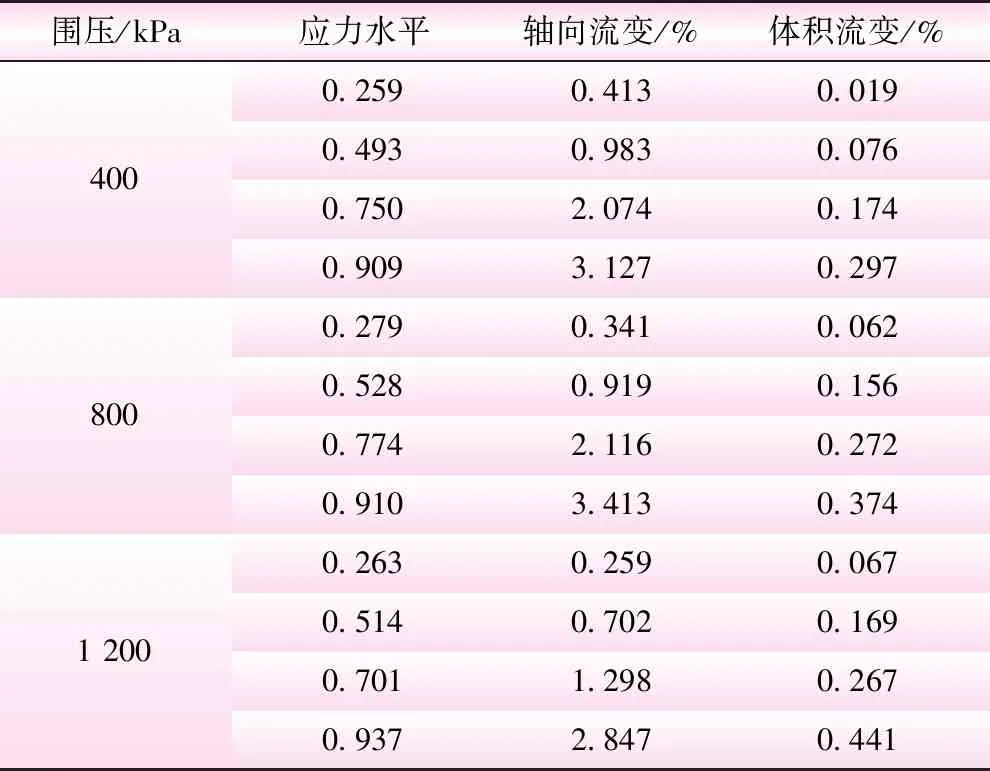
表4 最终流变应变计算值

图10 堆石料最终流变应变计算值

按照式(8)拟合最终流变量，得到式(16)和式(17)：

(16)

(17)

如果将式(17)中的剪应变εsf换成工程剪应变γsf，则有拟合结果

(18)

将式(16)和(18)给出的堆石料流变模型参数汇总，见表5。同时，将李国英等[5]对公伯峡面板堆石坝料的试验参数也列于其中。由表5可知，除m1偏小外，参数b、c、d、m2、m3的计算值与公伯峡堆石料试验参数接近。计算参数在工程经验范围之内，且符合堆石料流变工程特性，验证了本文提出方法的可行性。

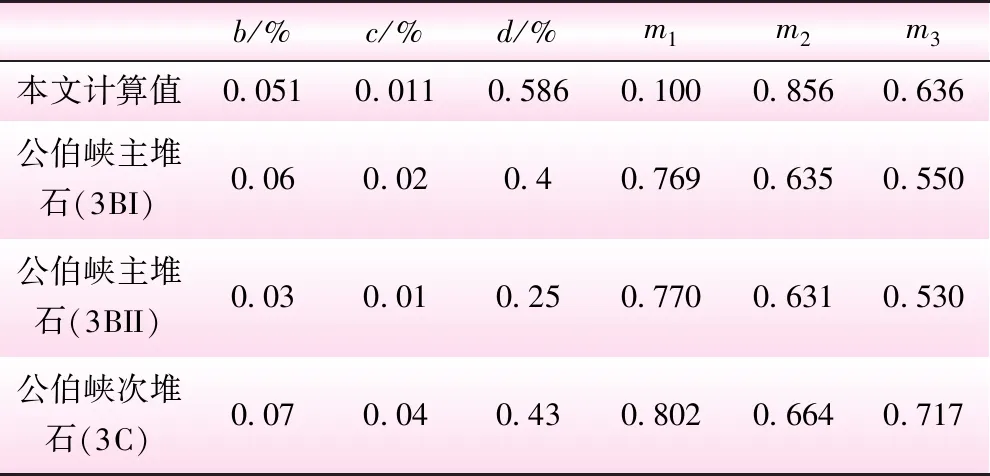
表5 堆石料流变模型参数

6 结 论

堆石料流变试验耗时过长，实际工程中流变试验工况覆盖坝料种类、级配与密度变化以及满足插值方法要求是困难的，只能进行几种简约工况的流变试验，会放大流变变形计算时的插值误差。因此寻求更简便的流变试验方法是必要的。

本文依据堆石料变形与颗粒破碎具有的强相关关系，认为堆石料流变变形与流变破碎具有对应关系。流变破碎指堆石颗粒受载一定时间后发生的破碎。设想可进行加载速率足够慢的三轴试验，即凡荷载形成的劈裂应力超过长期强度的颗粒有足够时间破碎。这样，试验得到的应力-应变-体变曲线必包含流变变形。与不含流变变形的常规三轴试验曲线进行比较，偏应力一定时，两种应力-应变曲线的差就是堆石料轴向流变变形，在体变曲线上查找对应点的体变差为体变流变。算例计算表明，通过计算得到的流变应变与试验值相当，流变模型参数符合预期。

计算中的关键参数是堆石颗粒的长期强度应力水平，即颗粒长期强度与瞬时强度之比，可通过颗粒流变试验确定，也可通过对应岩石的双扭试验测量起裂韧度与断裂韧度确定。颗粒流变试验采用双杠杆砝码加载，构造简单，多台联排可提高效率。双扭试验因不需模拟流变过程，耗时短、效率高。

中小型土石坝受工程规模等限制，一般不进行堆石料的流变试验，变形参数常参考已有试验数据与工程经验拟定，存在不确定性。本文提出的方法，利用必做的常规三轴试验数据和堆石颗粒的长期强度应力水平，直接推算堆石料流变变形，得到其流变模型参数，具有耗时短、效率高的优点。