双向串联谐振变换器固定载频积-移相控制策略

包浚炀, 李 勇, 段善旭

(强电磁工程与新技术国家重点实验室(华中科技大学), 湖北 武汉 430074)

1 引言

随着新能源发电系统的发展,新能源渗透率不断提升,储能技术作为灵活性资源,可以为电力系统提供变频、调峰等服务,已成为新型电力系统的技术支撑[1-3]。在储能系统中,连接直流母线和储能单元的双向DC-DC变换器需要具有双向变流能力和宽增益范围,以适配储能单元和直流母线电压、电流变化,其中,隔离型变换器因其优良的软开关、电气隔离性能,得到越来越多的关注[4]。

隔离型双有源全桥变换器(Dual Active Bridge,DAB)有高功率密度、高可靠性、双向结构对称等特点,得到了广泛的应用。但该拓扑效率受到高环流电流、高关断损耗、软开关范围较窄的限制。现有研究也提出了相关优化控制策略,解决了DAB变换器的部分问题[5-10]。

相比于DAB变换器,谐振型变换器通过在电路中加入谐振腔,使得变换器拥有更宽的调压范围,更好的软开关特性,可以实现开关管的零电压开通(Zero Voltage Switching,ZVS)和零电流关断(Zero Current Switching,ZCS)。按照谐振腔构成分类,现有拓扑主要分为串联谐振变换器、LLC谐振变换器、CLLC谐振变换器。

对于双向串联谐振变换器,传统脉冲频率调制(Pulse Frequency Modulation,PFM)无法实现升压的电压增益,且在轻载时失去电压调节能力[11],同时在调压过程中存在较大的无功环流[12,13]。现有相关研究提出了定频调制策略,采用移相调制方式对变换器进行控制。文献[14]采用了原副边基波同相的定频调制方式,实现了双向增益范围的拓宽与双向平滑切换,但是无法保证开关管的软开关,变换器效率不高。文献[15]提出了最小环流电流的三重移相角控制,实现了无功环流和开关管软开关的最优化设计,但是控制器计算量大、实现困难。文献[16]中采用了三电平拓扑,通过调节移相角和零电平占空比实现了宽电压范围,但在调压过程中易失去ZVS特性,且电路和控制均较为复杂。文献[17] 提出变频和副边延时开通的混合调制策略,实现了较窄变频范围内变换器的宽范围升降压控制,同时维持了开关管的ZVS,但是控制器需要电流过零信号,且无法实现双向自动切换,难以适应储能系统双向应用场景。

在串联谐振变换器中通过增加变压器气隙等方式,可以构成LLC谐振网络。LLC变换器解决了串联谐振变换器无法升压的问题,同时实现了原边开关管的ZVS和副边开关管的ZCS。但是在反向工作时谐振腔退化为串联谐振特性[18],且谐振腔双向特性不一致,双向平滑控制较为困难[19]。在副边串入谐振电容可构成CLLC型双向对称的谐振网络,但低压侧电容的电流应力较大,损耗和体积明显增加。相关学者提出利用辅助电感构成L-LLC型的双向对称谐振网络[20-22],同时引入了变频、移相等控制策略,实现了双向对称控制和自动模式切换,但是辅助电感的引入也增加了变换器的体积和损耗,不利于变换器的效率提升。

为了满足储能系统中双向DC-DC变换器宽双向增益范围、高效率、双向工作快速平滑切换的要求,本文提出了一种双向串联谐振变换器固定载频积-移相控制策略。该控制策略采用变频-移相混合调制,拓宽了双向电压增益范围。此外,分析并优化了变换器的软开关特性和环流特性,并设计了双向工作模式自动切换策略。为验证所提控制策略,搭建了额定电压340 V/52 V,额定功率2 kW的实验样机,对工作特性和双向切换过程进行了验证。

2 变换器工作原理

双向串联谐振变换器拓扑如图1所示。图1中Vbus为原边直流母线电压,Vbat为副边电池电压,开关管S1～S4构成原边全桥,S5～S8构成副边全桥,开关管的输出寄生电容分别为Coss1～Coss8。Vp和Vs分别为原边全桥、副边全桥的桥臂输出电压,Cr为谐振电容,Lr为谐振电感,Lm为变压器励磁电感,变压器的变比为N∶1,ir为谐振电流,im为励磁电流,it为变压器副边绕组电流。

图1 双向串联谐振变换器拓扑Fig.1 Bidirectional series resonant converter

2.1 双向工作原理

在变频移相调制方式下,变换器的开关频率始终高于Lr、Cr的串联谐振频率,且所有开关管导通时间均为开关周期的一半。在正向工作时,副边全桥相对于原边全桥的移相角φ>0,即副边全桥滞后原边全桥动作;反向工作时,φ<0。正向和反向工作波形如图2所示。

图2 变换器主要波形图Fig.2 Main waveforms of converter

图2(a)中,α、β为全桥电路电压、电流的相角,谐振电流ir滞后原边电压Vp的相位角为α,副边电流it超前副边电压Vs的相位角为β。

在t0时刻,原边开关管S1、S4导通,原边谐振电流和副边电流均快速上升至正值。在t1～t2的死区时间内,副边电流it为开关管结电容Coss5～Coss8进行充放电,实现S5、S8在t3时刻的零电压开通。

在t4～t5时刻,原边谐振电流ir在死区时间内为结电容Coss1～Coss4进行充放电,实现了原边开关管S2、S3在t6时刻的零电压开通。因此,当原边电流ir滞后全桥输出电压Vp,即α>0时,可以实现原边开关管的ZVS,同样当β>0也可以实现副边开关管的ZVS。

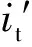
2.2 稳态分析

为了分析变换器的增益特性和相角特性,采用基波近似分析法,对双向串联谐振变换器变频移相调制方式下的稳态特性进行分析推导。

2.2.1 正向工作

正向工作基波等效电路如图3所示。由于副边电压电流存在相位差β,等效负载ZAC并非纯阻性。

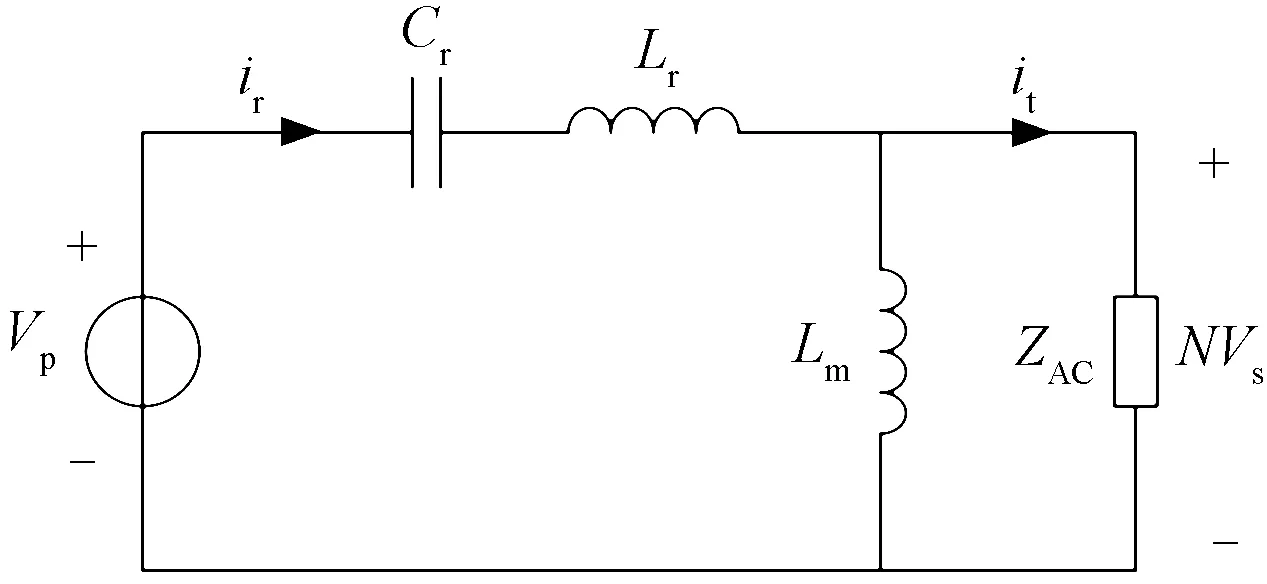
图3 正向工作基波等效电路Fig.3 Equivalent circuit under forward mode

根据有功电流和无功电流的关系可以得到副边电压电流相量表达式为:

(1)

式中,Po为变换器的输出功率。

因此,基波等效负载为:

(2)

式中,Zr和Q分别为谐振腔特征阻抗和品质因数,其表达式为:

(3)

(4)

根据图3等效电路,列写基尔霍夫电压、电流方程,如下:

(5)

式中,fs为变换器的开关频率。

根据图2中的相位关系和电压关系,并以原边电压Vp的相位角作为参考零相位,原边相位角α、副边相位角β、移相角φ和归一化电压增益G可表达为:

(6)

求解式(5)、式(6),并将式(2)代入,可以得出原边相位角α、副边相位角β、电压增益G的表达式,如下所示:

(7)

(8)

(9)

式中,Ln为励磁电感Lm和谐振电感Lr之比;fn为归一化频率,是开关频率与LC串联谐振频率之比,fn=fs/fr;k频率相关变量,k=fn-fn-1。

2.2.2 反向工作

反向工作基波等效电路如图4所示。与正向工作分析过程类似,通过电压电流方程和相位关系,求解基波等效电路,可以得出角度关系和变换器增益表达式,如式(10)～式(12)所示。

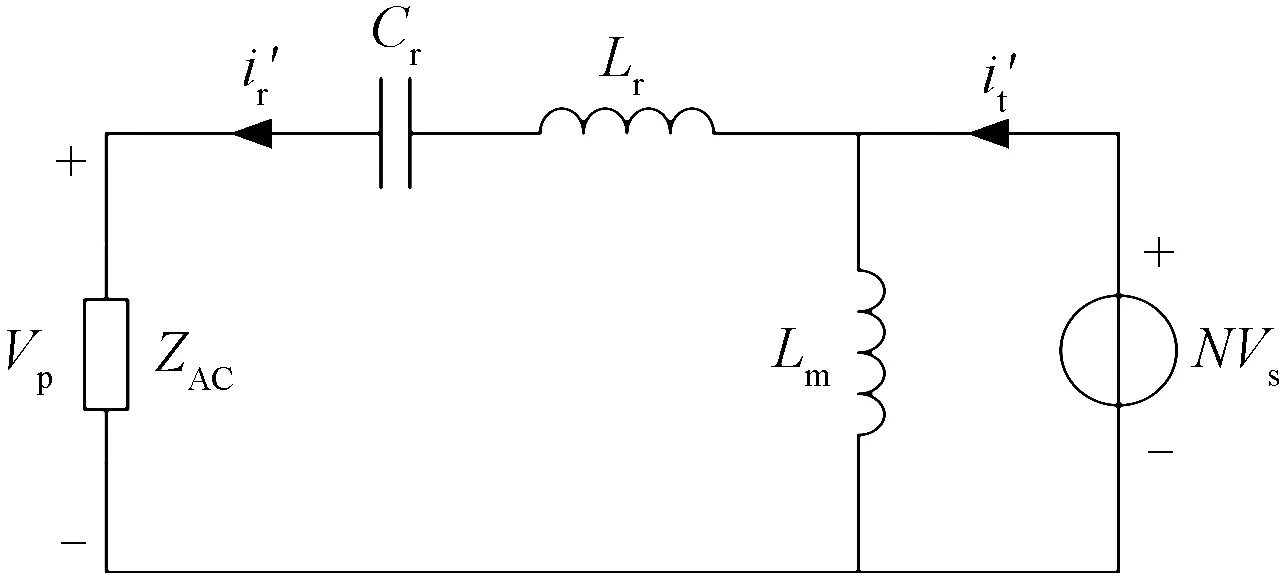
图4 反向工作基波等效电路Fig.4 Equivalent circuit under backward mode

(10)

(11)

(12)

式中,Q′为反向工作品质因数,如下:

(13)

2.3 增益特性

由式(9)、式(12)中增益表达式可以得出,变换器在正向和反向工作模式下均可以实现升压、降压运行,并且在引入移相角控制后,增益范围得到拓宽,变换器的控制也拥有了更多的自由度。

以正向工作为例,图5展示了谐振腔品质因数Q=0.8时电压增益与fn和φ的关系。相比于传统的变频控制,变频移相混合控制通过改变原副边全桥之间的移相角,在移相过程中增加了流入谐振腔的能量,因此电压增益随着移相角的增大而提高,且可以实现双向的升压变换。

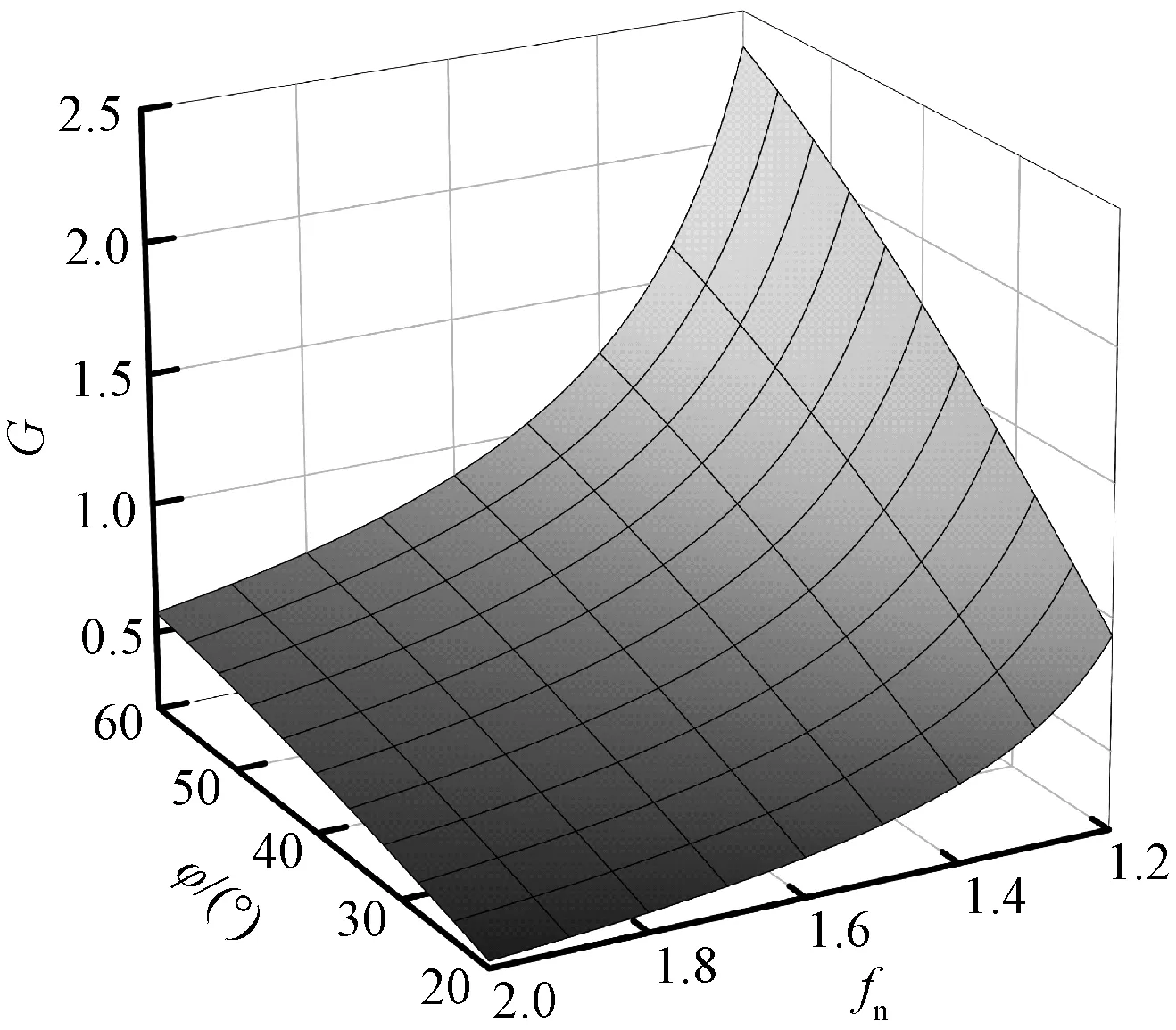
图5 Q=0.8时变换器的增益特性Fig.5 Voltage gain characteristics when Q=0.8

而当品质因数Q变化时,电压增益也随着品质因数的减小而增加,如图6所示。

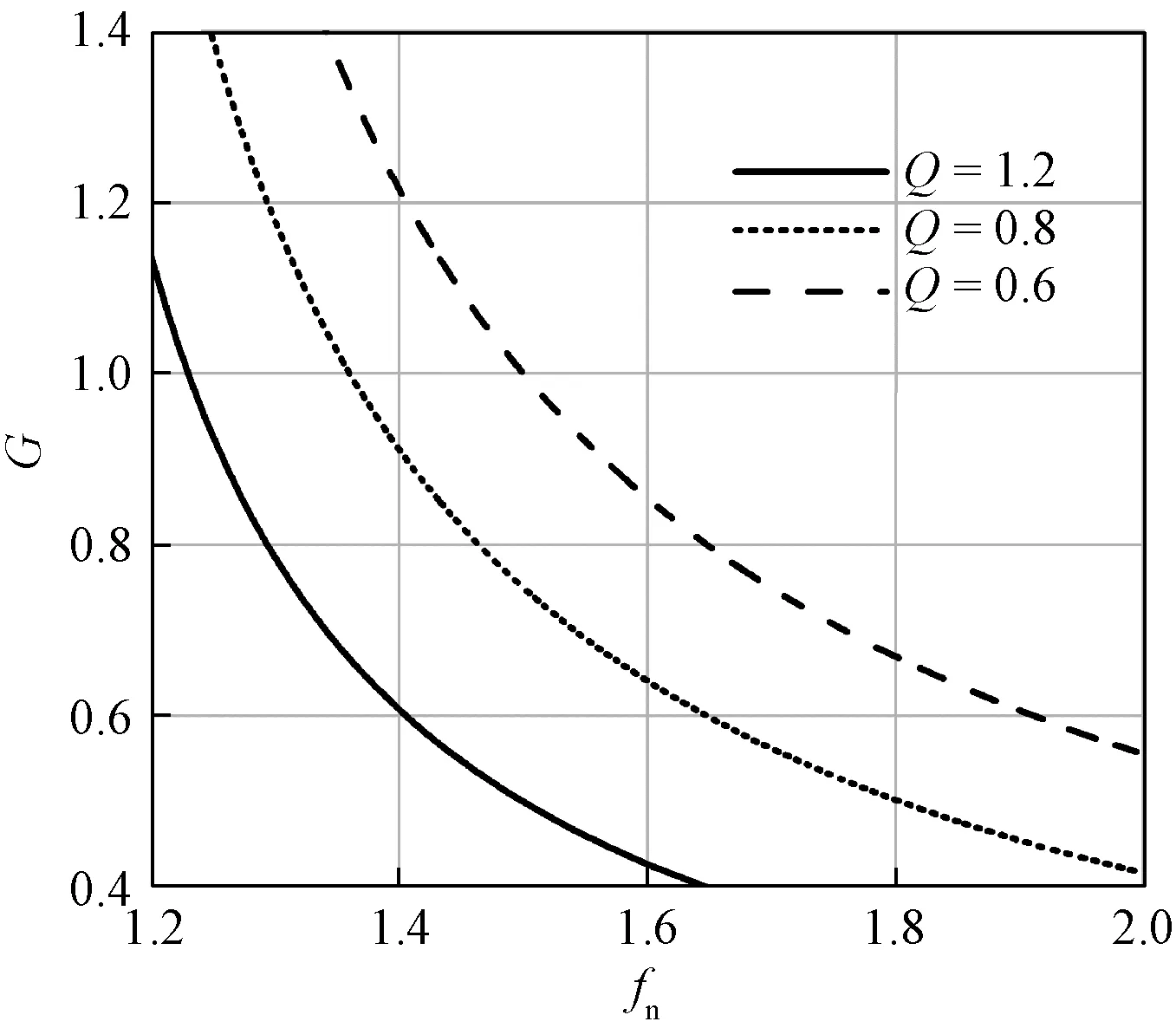
图6 增益与频率、品质因数的关系(φ=30°)Fig.6 Relationship between gain,frequency and Q when φ=30°

正反向品质因数的关系如式(14)所示:

(14)

式中,Ibat为副边电池侧的输出电流。

综合式(9)、式(12)中正反向增益和式(14)中品质因数的关系,可以统一变换器双向工作下电压增益表达式,如下:

(15)

由于变压器绕组始终受到副边全桥钳位,励磁电感不参与功率的传输,因此变换器正向工作和反向工作的谐振回路相同,工作模态类似,电压增益有统一的表达式,有利于变换器的双向运行和切换过程控制的分析和优化。

2.4 软开关特性

为了满足开关管ZVS开通的必要条件,需要维持谐振腔输入阻抗为感性,即α>0、β>0、α′>0、β′>0。代入式(7)、式(8)、式(10)、式(11)中阻抗角的计算,可以得出ZVS条件分别为:

(16)

(17)

(18)

(19)

式(16)、式(17)分别表示了正向工作时原边和副边ZVS的条件;式(18)、式(19)分别表示了反向工作原边和副边ZVS的条件,各个ZVS区域示意图如图7所示。若变换器的频率、移相角选择不当,谐振腔进入容性区域,将无法实现开关管的ZVS,导致变换器的开关损耗提升。为此,需要提出一种控制策略,维持双向工作条件下原边、副边实现所有开关管的软开关,提高变换器的效率。

图7 正向工作和反向工作ZVS区域Fig.7 ZVS region for switches in forward and backward mode

3 固定载频积-移相控制策略

由变换器ZVS条件和增益特性可以得出,品质因数Q和频率变量k的乘积影响了变换器增益范围和软开关特性,成为决定变换器工作特性的重要变量。因此定义Qk乘积为变量C,称C为变换器的“载频积”,如式(20)所示:

C=Qk=Q(fn-fn-1)

(20)

代入式(16)～式(19)可得,若变换器的增益范围确定,载频积的大小决定了变换器是否满足ZVS条件。因此,为了在给定增益范围内实现变换器所有开关管的ZVS,提高变换器效率,本文提出了一种固定载频积-移相控制策略:控制变换器的载频积C为优化选取的固定值,同时通过改变移相角调节变换器的增益。在该控制策略中,控制器测量负载的品质因数,当负载功率提高,品质因数Q增大,则控制开关频率降低;当负载功率降低,开关频率随之提升,以维持载频积为固定值。

3.1 增益特性

引入固定载频积-移相控制策略后,将式(20)代入式(15)可得,变换器增益特性将与负载功率解耦,仅与移相角φ有关,如式(21)和图8所示。

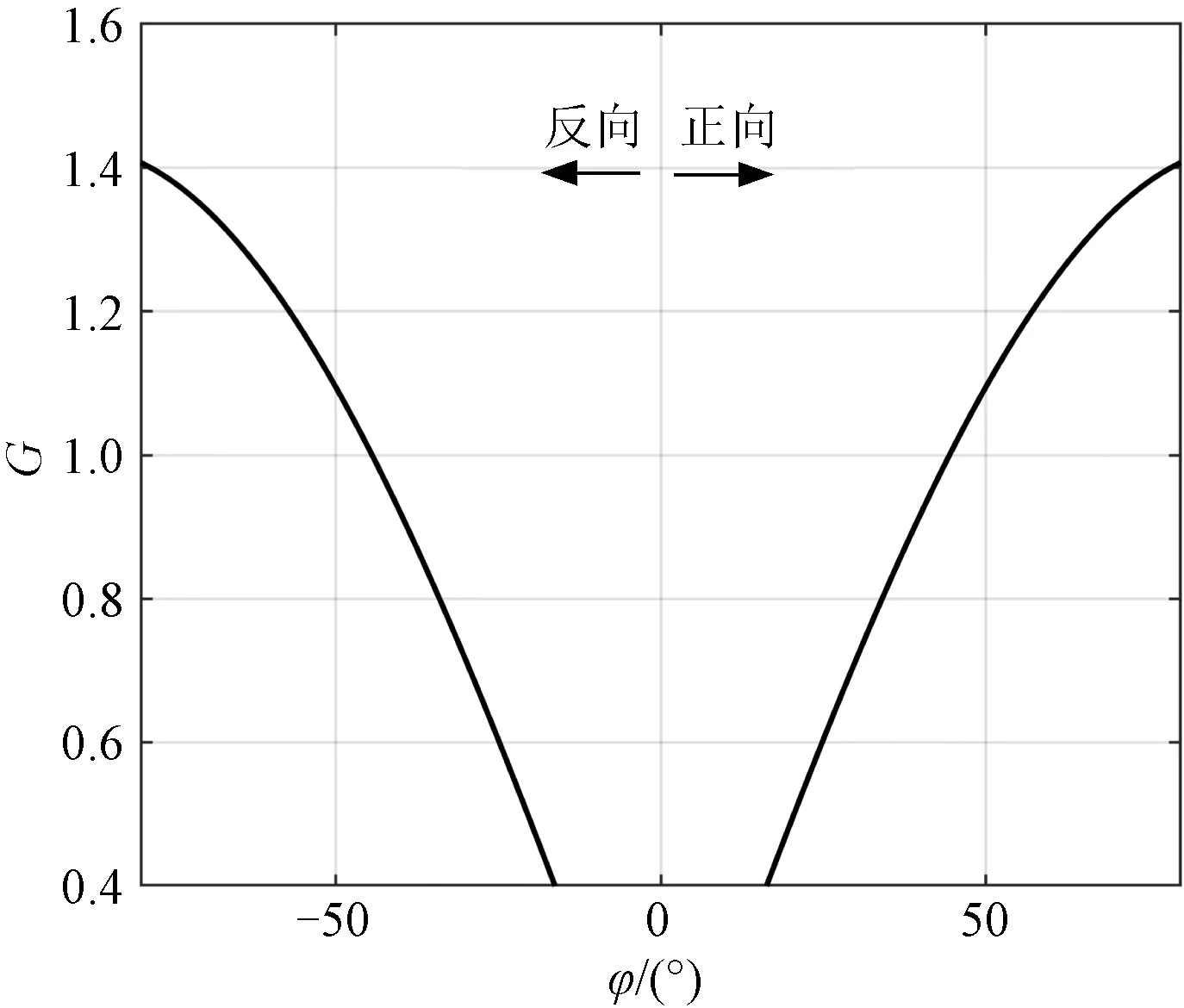
图8 固定载频积-移相控制策略下增益特性(C=0.7)Fig.8 Gain curve under proposed control strategy (C=0.7)

(21)

在正向工作和反向工作模式下,变换器电压增益特性对称,均可以实现升压工作,且在较宽的增益范围内变化。因此,可以通过改变变换器的移相角来调节变换器的正向、反向工作增益。

3.2 环流特性

当载频积满足ZVS条件,变换器所有开关管可以实现零电压开通,因此损耗主要来源于导通损耗。为了优化变换器的效率,减小导通损耗,需要对变换器谐振腔内的环流能量进行分析计算和抑制。

变换器谐振腔内的功率因数(Power Factor,PF)可以反映无功环流能量与输出能量的比例。根据谐振腔电压电流相位角表达式,可以分别推导出正向工作和反向工作的功率因数。以正向工作为例,功率因数表达式如式(22)所示。忽略影响较小的励磁电感,可以绘制功率因数与载频积取值、增益的关系,如图9所示。

(22)

由图9可以得出,在增益确定时,载频积的增大将导致谐振腔的功率因数降低。因此,为了抑制谐振腔内的无功环流,应限制载频积C的最大取值。

3.3 双向模式切换策略

根据式(20)可以看出,若负载功率减小直至空载,变换器为了维持载频积固定,会随着品质因数的减小而升高开关频率,若不进行限制,将影响变换器的正常工作。因此,为了实现变换器的双向工作模式切换,需要在式(20)的基础上,针对较低负载的运行工况进行优化,当功率较小时限制开关频率的上升,以维持正常工作,如式(23)所示:

(23)

式中,kmax为预设最大频率系数。

以电压增益G=1.2,最大频率fn_max=3,载频积C=0.7为例,移相角φ、归一化频率fn和功率的关系如图10所示,图10中,Pnor为额定功率值。

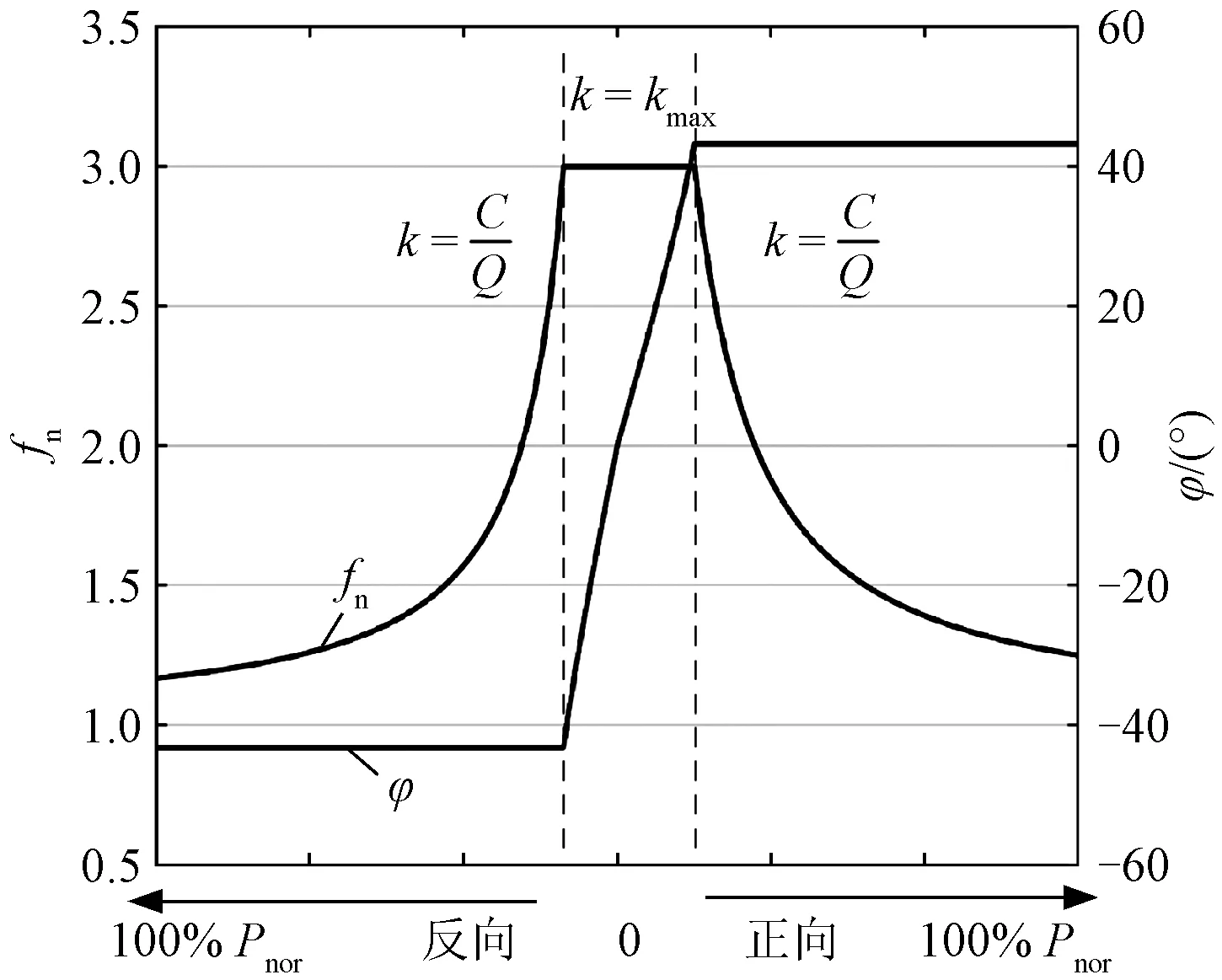
图10 移相角φ、归一化频率fn和功率关系曲线Fig.10 Plots of φ and fn with regard to output power

以正向额定功率切换至反向额定功率的过程为例,变换器首先处于k=C/Q的固定载频积区域,随着负载功率减小,变换器的开关频率升高,直至即将超过设定的最大开关频率时,变换器进入定频区域,移相角φ开始减小。当移相角变化为负值,即副边全桥超前原边动作时,变换器进入反向工作模式。随着反向功率增大,变换器重新进入固定载频积区域,开关频率降低,直至达到反向额定功率。

引入最大频率的限制后,变换器可以实现双向能量流动的自动切换,且过程中无控制策略的改变,可以保证切换过程的平滑、快速。

3.4 控制策略实现

综合上述分析,固定载频积-移相控制策略的控制框图如图11所示。

图11 固定载频积-移相控制框图Fig.11 Block diagram of proposed control strategy

以副边电流闭环控制为例,控制器测量副边电压、电流,计算当前的品质因数Q,进行固定载频积控制,并对最大频率进行限制,得到变换器的开关频率fs。同时,闭环控制器对副边直流侧电流进行控制,得到移相角φ,最终生成开关管的驱动信号。

4 载频积参数优化设计

本文双向串联谐振变换器具体电路参数见表1。

表1 双向串联谐振变换器参数Tab.1 Parameter of bidirectional series resonant converter

为了实现变换器所有开关管的ZVS,需要对载频积的取值进行限制,以满足谐振腔感性阻抗的条件。假设所有工况下,归一化频率fn>1.2,可以计算出式(16)～式(19)中对载频积C的限制,如式(24)所示:

(24)

式中,增益最大值Gmax=1.21;增益最小值Gmin=0.82;频率最小值fn_min=1.2。

为了保证所有增益条件下变换器不进入容性区域,以维持原边、副边所有开关管的ZVS,载频积应同时满足式(24)中的所有限制条件,如式(25)所示:

C>0.681

(25)

同时,为了抑制谐振腔内的无功环流能量,优化变换器效率,限制额定工作条件下,功率因数PF>0.9,代入式(22)可以计算出载频积的对应限制条件为:

C<0.722

(26)

为了同时满足式(25)、式(26),以减小变换器环流能量,提高变换器效率,并实现所有开关管的ZVS,选择载频积C=0.7,此时变换器的工作区间如图12中黑色粗线所示。在工作区间内,变换器始终保持较高的功率因数,且处于实现双向工作ZVS的区域。

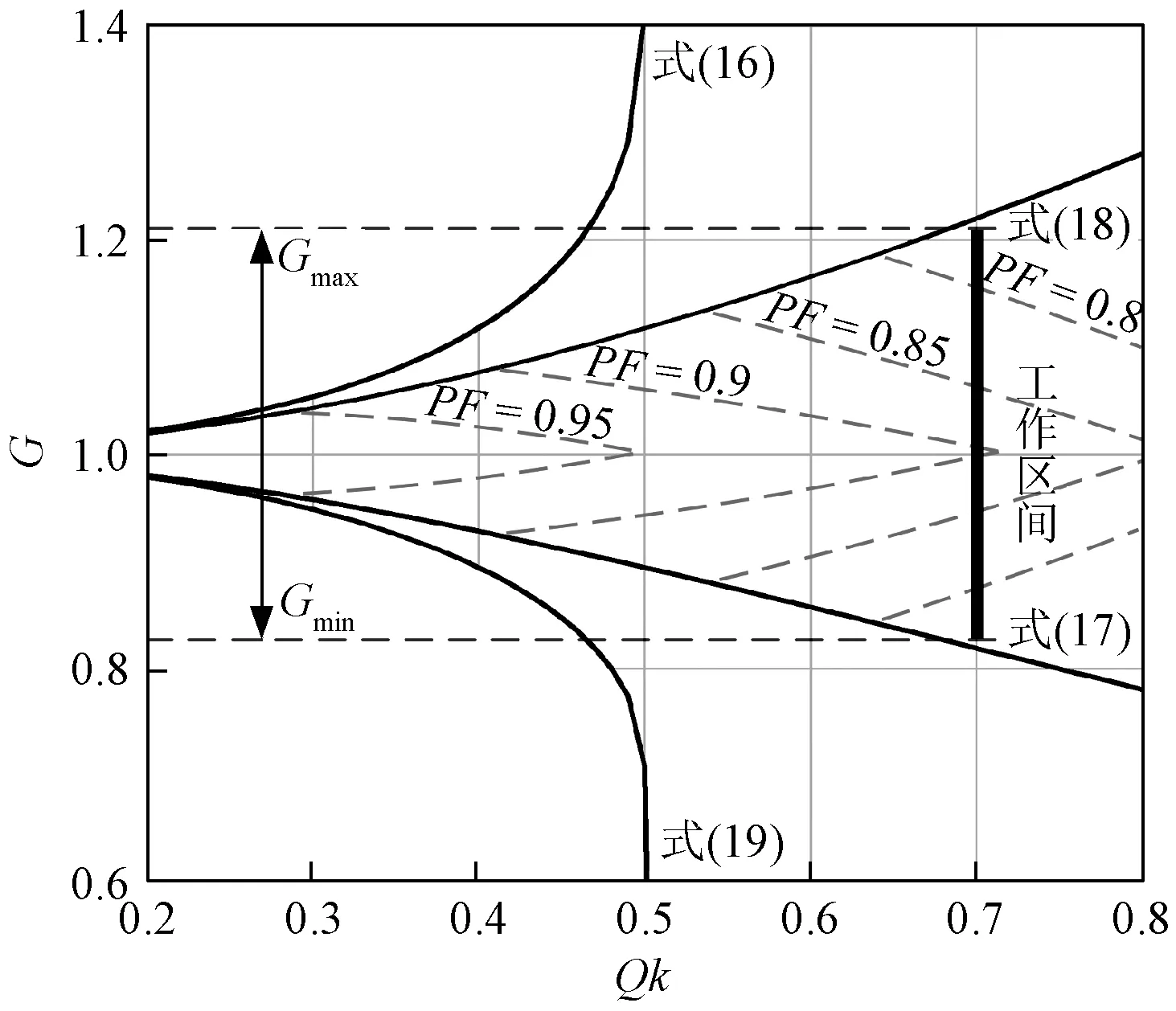
图12 工作区间示意图Fig.12 Operating region of proposed control strategy

在该载频积参数下,额定工况的功率因数为0.91,在增益变化时最低功率因数为0.78,可以将无功环流能量控制在较低的水平。在该条件下,变换器最大品质因数Q=1.79,计算可得此时最小归一化频率fn=1.21,因此满足前文fn>1.2的假设。限制变换器最大开关频率fn_max=3,以实现轻载下变换器的正常工作和双向工作模式的平滑、快速切换。

5 实验验证

为验证本文所提控制策略,搭建了原边额定电压340 V、副边额定电压52 V、额定功率2 kW、参数如表1所示,实验样机如图13所示。原边开关管选用C2M0025120D,副边开关管选用CSD19505,并采用Xilinx公司的嵌入式平台ZYNQ7010对变换器进行控制。

图13 双向串联谐振变换器实验样机Fig.13 Experimental prototype

图14(a)和图14(b)分别展示了变换器正向工作在额定电压条件下2 kW满载和20%负载的波形。变换器满载工作时,开关频率约为96 kHz,略高于谐振频率;而20%负载时变换器开关频率提升至200 kHz,维持了载频积为固定值。从实验波形可以看出,原边全桥和副边全桥的输入阻抗均呈感性,实现了所有开关管的ZVS开通。此外,由于增益固定,在负载功率变化时变换器的移相角几乎不发生变化,验证了电压增益与负载功率的解耦特性。

图14 正向工作稳态波形Fig.14 Waveform of forward mode operation

图14(c)和图14(d)分别展示了在额定功率下G=1.21和G=0.82变换器的工作波形。可以看出,变换器的移相角随着增益的增大而增大,验证了电压增益关于移相角的特性。同时,在增益变化后,谐振腔电压、电流的相角也发生了变化,但仍然维持了感性特性,保证了增益变化时原副边所有开关管的ZVS开通,同时也维持了较高的功率因数和较低的环流能量,验证了载频积参数优化设计的效果。

图15(a)～图15(d)展示了变换器反向工况的稳态工作波形。与正向工作相比,反向工作的副边全桥电压相位超前于原边全桥输出电压,实现了功率的反向传输。由于励磁电感较大,原边、副边的谐振电流与正向工作相比波形较为类似,且都维持了感性的输入阻抗,实现了所有开关管的ZVS和较低的环流能量。

图15 反向工作稳态波形Fig.15 Waveform of backward mode operation

图16展示了双向满载加换的副边输出电流Ibat的波形。从实验结果可以看出,变换器实现了双向工作模式的快速切换,正向至反向满载和反向至正向满载的切换时间分别为2.36 ms和2.66 ms,且由于双向切换无需改变控制策略,切换过程平滑无冲击。

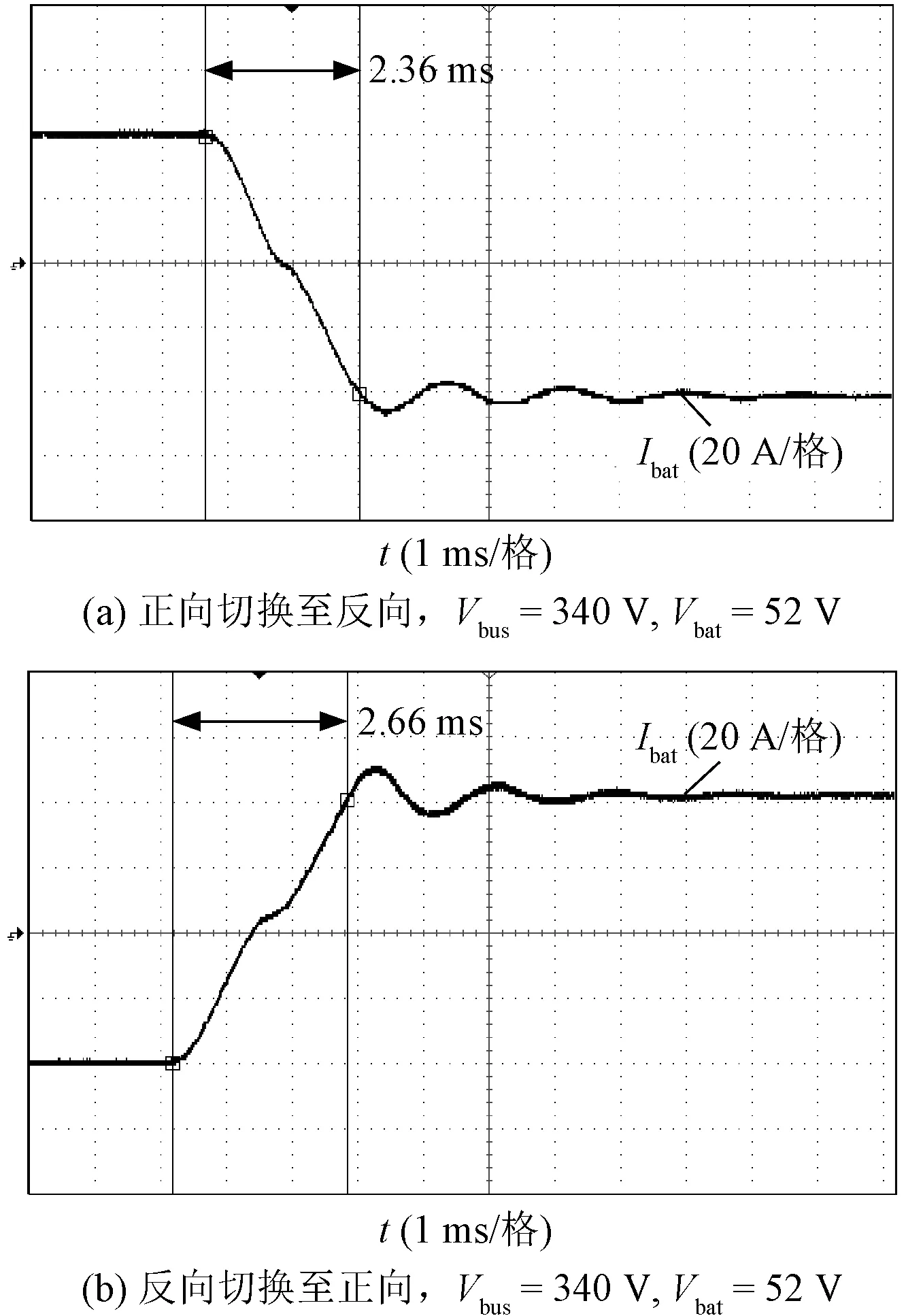
图16 双向满载-满载切换副边电流瞬态波形Fig.16 Waveform of forward and backward mode transition

图17、图18展示了变换器实测效率曲线。变换器在额定电压条件下正向、反向的满载效率分别可以达到97.38%和96.97%。当变换器的电压增益变大时,谐振腔品质因数降低,导致导通损耗提升,变换器效率η下降。而当输出功率减小,变换器开关频率提升,损耗占比提高,也会导致效率的下降。若采用等效导通电阻更低的开关管和电感、变压器,效率可实现进一步提升。

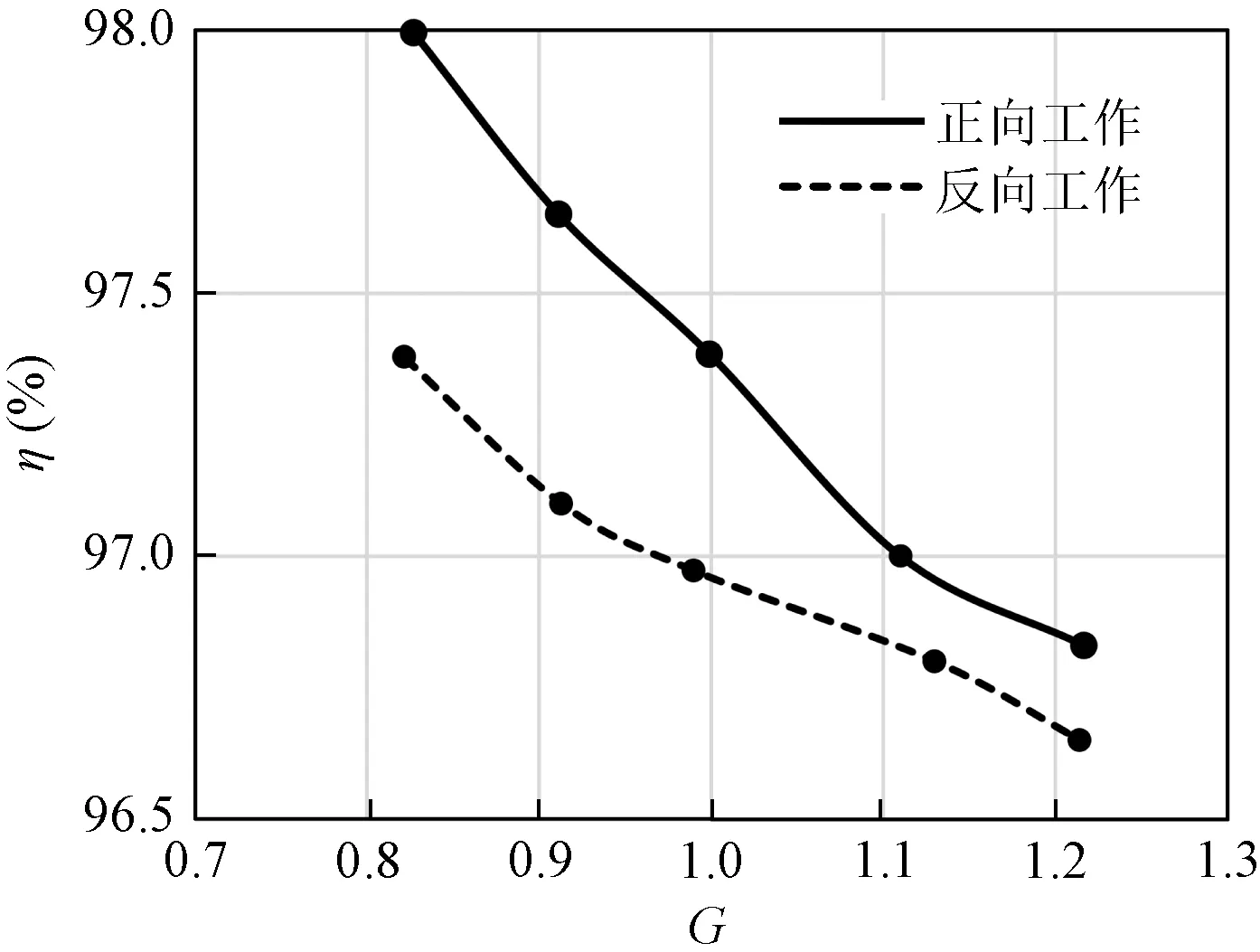
图17 变换器效率曲线,Po=2 kWFig.17 Efficiency curve of proposed converter, Po=2 kW

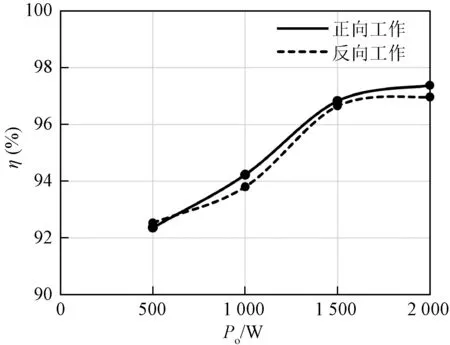
图18 变换器效率曲线,G=1.0Fig.18 Efficiency curve of proposed converter, G=1.0

6 结论

本文提出了一种双向串联谐振变换器固定载频积-移相控制策略,实现了变换器双向电压增益范围的拓宽,维持了所有开关管的ZVS,并且优化了环流特性,提高了变换器的效率,样机正向和反向工作效率分别可达97.38%和96.97%。此外,所提控制策略可以实现双向工作模式自动切换,双向满载切换时间均小于3 ms,过程快速平滑,适合需要宽增益范围、高效率性能和快速充放电切换的储能系统应用场景。