量子元胞自动机三输入标准函数的优化设计
2023-10-30解光军张永强
张 辉, 解光军, 张永强
(合肥工业大学 微电子学院,安徽 合肥 230601)
0 引 言
尽管互补金属氧化物半导体(complementary metal-oxide-semiconductor,CMOS)的特征尺寸一直在缩小,但芯片集成密度的增加遇到了新的挑战,其中重要的影响因素是漏电功耗和隧道效应[1-3]。针对这一问题,研究人员一直在寻找可以替代CMOS的新器件。量子元胞自动机(quantum cellular automata,QCA)由于其特征尺寸小、超低功耗和高工作频率,成为有力的候选者。QCA电路由规则排列的QCA元胞组成, 每个QCA元胞由4个量子点和2个额外的自由电子组成。4个量子点位于一个假想的正方形的四角,电子可以在正方形中相邻的量子点之间隧穿。由于库仑力的排斥,电子很容易占据2个对角量子点,以这种方式可形成2个稳态,分别代表二进制逻辑0和1。同时,随着QCA电路设计系统的发展,导线交叉成为不可低估的问题,它不仅会消耗额外的资源还会增加QCA电路的复杂性[4]。
近年来,很多研究者已经不满足于只使用择多门和反相器来设计QCA电路,越来越多结构简单、功能多样的逻辑门相继被提出,包括两输入XOR、XNOR、三输入异或门(XOR3)、多路复用器(Multiplexer,MUX)等,利用这些门设计的电路可能带来一些显著的优势,如使用XOR3和择多门实现全加器[5]、使用MUX构建的RAM单元[6]、使用XOR设计奇偶发生器[7]。这些新提出的电路结构不仅比只使用择多门和反相器设计的电路更简单,而且电路结构的逻辑更加直观易懂。本文尝试使用上述多种逻辑门来重新设计三输入标准函数,以达到优化电路的目的。
1 QCA基本概念
1.1 QCA时钟
QCA时钟包括切换、保持、释放和松弛4个阶段,以控制元胞之间的数据流动、驱动单元和提供功率增益[8]。4个连续的时钟(clk0、clk1、clk2、clk3)为一个周期,相邻时钟之间的相位差为90°,元胞间的数据在4个时钟间循环传输[9]。
QCA电路共有3种交叉方式,分为共面交叉和异面交叉,其中共面交叉分为基于旋转元胞和基于QCA时钟2种交叉方式。QCA电路中的数据只能在同一时钟或相邻时钟内传输信息,不能在不相邻时钟之间传输信息。因此,当clk0和clk2的传输线或clk1和clk3的传输线交叉时,信息是独立的,不会相互干扰,基于QCA时钟的导线交叉如图1所示。
1.2 择多门和反相器
择多门是QCA电路中的一种基础逻辑门,包括3个输入(A、B、C)信号和1个输出信号F。择多门的QCA电路如图2所示,逻辑表达式为:

图2 QCA电路的基本逻辑门
F=AB+AC+BC
(1)
当择多门的1个输入被置为“0”或“1”时,可以得到1个对应的与门和或门。
反向器本质上是一个非门,在QCA电路中通过与门、或门和非门可以完成大部分电路的设计。
1.3 XOR、XNOR、XOR3和2-1 MUX
以往的研究者在设计三输入标准函数时大多只使用三输入择多门和反相器,随着QCA电路的发展,已经有研究人员使用XOR3设计三输入标准函数。本文在此基础上,不仅使用择多门和XOR3,更是加入了两输入XOR门、XNOR门和2-1 MUX,这使得所提出的电路结构更加简洁和直观。QCA电路中的2-1 MUX和XOR3如图3所示。图3中,输入B为选择端,2-1 MUX逻辑表达式为:

图3 QCA电路中的2-1 MUX和XOR3
(2)
XOR3的逻辑表达式为:
F=A⨁B⨁C
(3)
QCA电路的两输入XOR和XNOR如图4所示。
2 三输入标准函数

1) 1个点。F1=ABC。
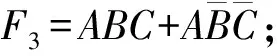
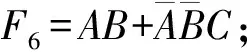
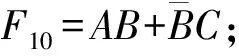


图5 立方体表示的三输入标准函数
(4)

A⨁B⨁C
(5)
3 13种标准函数的优化
简化后的13种标准函数的QCA电路如图6所示,具体的优化过程如下。
标准函数8:该函数不需要逻辑门,只需直接将输入输出相连即可。
标准函数1、2、5、9:这4个函数在本文中采用以往的设计,使用则多门来实现的方法,并没有优化的空间。
标准函数3、10、12、13:这4个函数通过使用新的逻辑门,使得电路结构相对以往只使用则多门和反相器所设计的电路,带结构上更加简单。
标准函数3的化简结果为式(6),通过使用XOR,简化了电路结构。
(6)
从标准函数10的表达式可以看出,只需要一个2-1MUX即可实现函数功能。同理,标准函数12也只需要一个XNOR,标准函数13使用一个XOR3即可完成函数功能。
标准函数4、6、7、11:这4个标准函数无法直观得到简化后的方程,本文的主要工作也是对这4个函数进行优化。
标准函数4优化后的表达式为:
(A⊙B)(B⊙C)
(7)
标准函数6优化后的表达式为:
(A⊙B)(B+C)
(8)
标准函数7优化后的表示式为:
(A+B)(A⨁B⨁C)
(9)
标准函数11优化后的表达式为:
(A+C)⊙B
(10)
4 仿真与分析
标准函数4、6、7、11的仿真结果如图7所示,通过仿真波形可以看出所设计QCA电路的正确性。其余的标准函数由于逻辑相对简单,仿真结果不再展示。

图7 部分标准函数的仿真结果
本文所设计的13种标准函数的相关参数见表1所列。

表1 13种标准函数的参数
表1包含了每个标准函数简化后的表达式,需要的元胞数量、占用的电路面积和延迟周期。本文设计的13种标准函数与之前设计的参数对比见表2所列。

表2 标准函数的参数比较
通过比较,本文的设计与以往最好的设计相比, 在元胞的总数量上优化了18.4%,在总的面积上优化了15.4%,在总的延迟方面优化了21.2%。并且本文设计的13种标准函数实现了导线的零交叉,这是以往的设计所没有实现的。
5 结 论
本文在前期研究的基础上,将多种新颖的逻辑门应用到13种标准函数的设计中。结果表明,新设计的标准函数QCA电路不仅各方面参数都有所提升,还实现了无导线交叉。下一步计划将这13种标准函数应用到更多、更复杂的电路设计当中。
