徐州市大沙河河道治理工程边坡稳定性分析

2023-10-30刘攀郭连峰纪凤杰王朝黄伟

珠江水运 2023年19期

◎ 刘攀郭连峰纪凤杰王朝黄伟

1.徐州市水利建筑设计研究院有限公司；2.盐城市水利勘测设计研究院有限公司

黄泛区形成的宽浅漫滩河流，河道两岸大多由黄河冲积的粉砂构成，地势高亢，土地瘠薄，河床因自然冲积形成，宽浅弯曲，两岸堤身单薄，且残缺不全，汛期洪水行洪不畅，经常漫溢成灾[1]。平时河床无水时，飞砂弥漫，一遇来水又极易冲蚀，造成严重水土流失和淤积河湖。河道淤积影响排涝、行洪需要进行清淤疏浚，但是在清淤过程中会影响河道边坡的稳定性。前人对一般边坡稳定性研究进行了充分研究[2,3]，但是针对黄泛区的河道岸坡研究较少，本文以黄泛区大沙河为研究对象，对河道治理工程边坡的稳定性进行分析与评价，同时为同类型的研究提供一定的参考。

1.工程概况

本次治理大沙河长32.6k m，河道底宽5 0 ～1 9 0 m，河底高程34.0m～30.0m，边坡1:3～1:4，现状滩面高程39.8～35.0m，宽约50～200m，李庄闸下入湖口处，局部相对较窄，甚至无滩面。两岸堤防基本连续，堤防一般高3～5m，堤顶高程43.0～40.0m，堤顶宽度2～5m，边坡1:3。根据现场勘查，堤身无裂缝、塌陷、跌窝等险情不良工程现象，但沿线堤防主要存在堤防沿线建筑物及穿堤道路位置多存在堤防缺口等问题。

2.堤防岸坡设计

2.1 堤型的确定

本次治理河道中心线基本沿原河口中心线走向，向两侧开挖，开挖河道中心线与原河道中心线基本一致或与原河道中心线基本保持平行[4]。针对微弯段进行适当切角抹弯。为了减少工程量，弯道段基本维持现状弯道半径，不作裁弯取直。

河道堤线的布置应根据河流走势，以河道洪水流向为主，尽可能兼顾原有河道和河岸线的弯曲形态，保留原有弯直河道，在原有河槽基础上固定凹岸，并充分利用原存河岸及河道两侧人工建筑物等特点，实现上下游平顺衔接，以确保分洪安全和河势稳定[5]。

根据该河道堤防的特点、堤址地质条件、复堤土料、工程结构及填筑方式，确定设计堤型为均质土堤，复堤土料为河道开挖土方，堤顶宽度为10m，迎水坡为1:4、背水坡为1:4。

2.2 河道边坡高程计算

根据《堤防工程设计规范》（GB50286-2013），堤防高程按设计洪水位加堤身超高确定，堤身超高计算如下：

式中：Y为堤身超高/m；e为设计风壅水面高度/m；R为设计波浪爬高/m；A为安全加高/m，本文治理河道属于3级堤防，所以取A=0.7m。

在确定江河等内陆水域堤防高程时，非常有必要考虑风壅水高度。在有限风区下的风壅水面高度可以按以下公式进行计算：

式中：V为设计风速，大沙河以东南风为主导风向，风向与波浪近似认为同一方向，按照计算波浪的风速20.0m/s确定；K为综合摩阻系数，取3.6×10-6；F为风区长度，计算点风区长度为600m；β为计算风向与堤岸轴线法线的夹角，取β=45°。河道20年一遇设计水位至设计滩面的平均水深为2m左右，经计算得到e=0.02。

根据《堤防工程设计规范》（GB50286-2013）。在风的直接作用下，正向来的波在单一斜坡上的波浪爬高的计算公式如下：

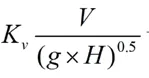
根据风壅水面高度和波浪爬高计算，堤防超高Y=0.02+0.62+0.7=1.34m，为了安全保留，取Y=1.5m。

3.河道边坡稳定性计算

3.1 渗流稳定计算

水在土体内渗透会引起土体内部应力状态的改变，从而引起土体内部原有的稳定条件发生变化，造成渗透破坏，同时土体渗透性的强弱，对土体的固结、强度发展及工程施工都有很大的影响。根据Darcy定律和渗流连续方程，对于饱和—非饱和土体中的渗流，连续方程如式（4）所示。

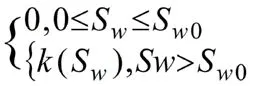
选取河道深度相对较大、地质复杂断面桩号5+050左岸、20+560左岸、29+200右岸、54+100左岸和57+500右岸作为典型断面进行渗透计算作为典型断面进行渗流计算，该断面各土层的渗透系数和相关地质参数详见地质勘查报告，这里不再赘述。

场地内第①层砂壤土夹粉砂渗透变形破坏类型为流土型，建议允许水力比降为0.30，通过计算河道边坡渗透稳定计算来判定岸坡是否发生破坏，计算结果如表1所示。

表1 河道边坡渗流稳定计算结果

3.2 边坡抗滑稳定验算

河道边坡分析施工期和行洪稳定渗流期临水侧堤坡的稳定性，采用瑞典圆弧条分法计算抗滑安全系数。其基本原理是：当土体发生破坏时，土中应力条件比较复杂，滑面上各点的抗剪强度分布同该点法向压力有关且是不均匀的。将滑移体进行垂直条分，忽略土条两侧条间力，假设土体内的圆弧破坏面的土体均绕一个圆心转动，当其滑动力矩大于抗滑力矩时，则边坡不稳，反之，边坡稳定性良好，瑞典条分法计算公式见式（5）。

式中：FS为安全系数；MR为滑移面上土条抗滑力矩之和；MT为滑移面上土条抗滑动力之和；Wi为第i块土条的质量；αi为第i块土条剪切面与水平面的夹角，φi为第i块土条滑动面的内摩擦角；ci为第i块土条粘聚力；li为第i块土条滑弧弧长。

本工程堤防边坡抗滑稳定性，按照规范计算施工期和设计洪水位下稳定渗流期两种工况下的边坡稳定性。在施工期，由于疏浚河道治理工程的开展，河底淤泥被清除，河岸边坡渗流场和应力场发生变化，坡体内将受到高剪切力和有效应力改变而出现滑坡的危险，并且这种可能出现的滑坡模式为典型的牵引式发展模式。行洪稳定渗流期，河道水位上升引起边坡内外水头差进而产生由坡内向坡外的渗流力来抑制边坡塑性区发展，水位上升初期能提升边坡稳定性，但随着水位趋于稳定，水位荷载的影响会导致滑移面向深处发展。本研究以断面桩号5+050左岸、20+560左岸、29+200右岸、54+100左岸和57+500右岸作为典型断面分析两种工况下的边坡稳定性，计算方式如图1、图2所示。计算结果如表2所示。

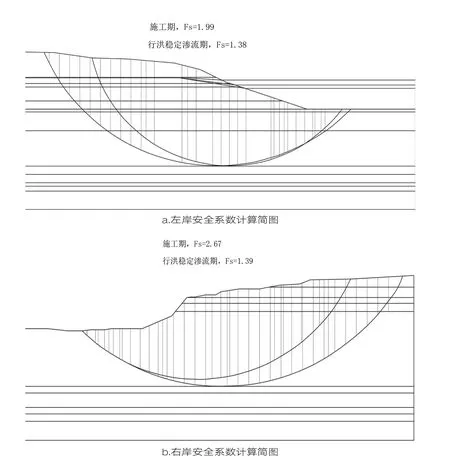
图1 边坡稳定性计算简图

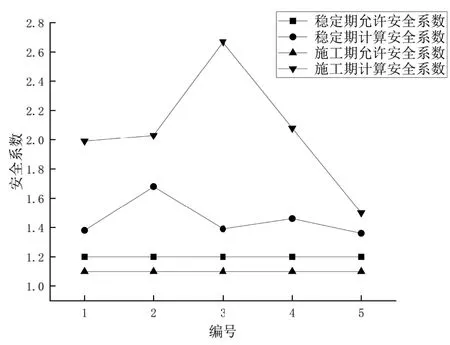
图2 边坡安全系数计算图

表2 边坡稳定性计算值

根据规范施工期的边坡安全系数最小值不能低于1.1，设计洪水位稳定渗流期的最小安全系数不能低于1.2，本研究工程根据瑞典圆弧法求得的安全系数趋于保守，但是计算值均满足要求，5个型断面的计算结果，安全系数最小的57+500右岸断面达1.5，远大于1.1。而稳定渗流期断面计算值最小为1.36，大于规范要求1.2，所以采用1：4坡比进行放坡处理和河道疏浚，河岸边坡的稳定性可得到保证。