面向二维移动机器人的路径规划算法综述

王 旭，朱其新，朱永红

1.苏州科技大学 电子与信息工程学院，江苏 苏州 215009

2.苏州科技大学 机械工程学院，江苏 苏州 215009

3.江苏省建筑智慧节能重点实验室，江苏 苏州 215009

4.苏州市共融机器人技术重点实验室，江苏 苏州 215009

5.景德镇陶瓷大学 机电工程学院，江西 景德镇 333001

机器人起源于20 世纪，由Fryer[1]和Carrera[2]在Vaucanson 和Jaquet 构造的类人机器人基础上做的研究。在工业革命结束时，机器人技术的进步促进了不同科学领域的发展，并创造了大批新设备以应用于不同领域之中，如建筑、军事、航空、运输等。机器人是由图1中的几个系统组成的，本文主要研究其控制系统中的路径规划技术。

图1 机器人的六大系统Fig.1 Six systems of robot

移动机器人通常应用于各种复杂的环境中，图2展示了四种场景下的移动机器人。在各个领域都有特定功能的机器人来为人类服务[3-4]，以完成各种任务[5]，包括探索未知的环境、搜索被困的受害者和携带重要材料等。在紧急和危险的场景中，移动机器人甚至可能是不可替代的[6]。然而，自主移动机器人的路径规划问题是当前难以解决的问题之一[3]。路径规划的目的是以最优的方式生成从起点到目标点可行的安全路径，避免自主移动机器人运动过程中可能发生的所有碰撞[7-8]。路径规划在静态地图环境中，一般在机器人进行移动之前就需要找到整个解决方案。与之不同的是，对于动态以及局部已知的环境，通常需要实时规划，并且需要更多的计划更新时间。移动机器人路径规划的主要问题一般是计算的复杂性、路径最优值的存在和整体适应性[4]。在二维移动机器人路径规划算法领域，大部分研究的目的在于找到最优解，但是随着生产技术的发展，最优路径已经不能满足需求。所以，在最优路径、收敛速度、平滑性、搜索速度等条件中进行统筹兼顾的改进是此领域内的最大任务和难点，也是研究的大势所趋的方向。

图2 各个领域的移动机器人Fig.2 Mobile robots in various fields

1 路径规划研究现状

路径规划是机器人学的基本问题之一[9-10]，也是研究最多的问题。目前，移动机器人路径规划领域的研究者们已经开发了许多技术，是当今研究的热点[11]。早期开发的确定性规划技术表明，即使对于简单的系统，它的计算要求也很高[12]。确切的路线图方法是早期路径规划的主要方法，如可见性图[13]、Voronoi图[14]、Delaunay三角图[15]和自适应路线图[16]，这些方法试图捕捉机器人搜索空间的连接性。而诸如Dijkstra 和A*等搜索算法被用来在连通性图中寻找最优解，D*则是针对动态图的。图搜索方法的使用涉及到工作空间的离散化，其性能在高维度上有所下降。有效的离散化可以以牺牲完整性为代价，而高分辨率的离散化在计算上是昂贵的。新型计算方法的出现激发了它们在路径规划中的应用。模糊逻辑控制[17-18]、神经网络[19]、遗传算法[20-21]、蚁群优化[22]和模拟退火[13]等方法都被应用于机器人路径规划。

二十一世纪以来，随着人工智能、传感器、网络和通信技术的快速发展，研究者们开始重视机器人的智能化[23]。在执行任务时，机器人需要使用路径规划技术对环境进行建模并定位其位置，控制运动，检测障碍物并避开障碍物。从起点到目标点的安全路径规划（通过检测和避开障碍物）是移动机器人的最基本的功能。因此，作为移动机器人研究的重要组成部分，路径规划技术将直接影响移动机器人完成任务的效率。

本文通过将路径规划算法划分为全局和局部两部分，注重对启发式路径规划算法进行梳理归纳和全面评述。对Dijkstra 算法、A*算法、RRT 算法、遗传算法、人工势场法、模拟退火算法、D*算法、蚁群算法、模糊推理法、强化学习法进行了深入分析。引用了领域内最新的文章，结合对各个算法的改进策略，对改进后的算法，在优势、局限性和适用场景三个方面进行比较。

2 基于先验信息的全局路径规划

全局路径规划一般属于离线（静态）的规划，移动机器人需要事先掌握地图所有的环境信息，综合先验完全信息来进行路径规划。在这种问题中，障碍物的位置一般是固定的。应用于此类问题的算法有：Dijkstra算法、A*算法、RRT算法、遗传算法等。

2.1 Dijkstra算法

1956 年，由Dijkstra 首次发现迪杰斯特拉算法[24]。Dijkstra 算法作为典型的求解最短路径的算法，经常被用于计算移动机器人在运动过程中单个节点到目标节点的最短路径[25]。其主要特点是以源节点为中心向外，通过迭代来选择下一个节点进行层层扩展，为了确保每一次迭代行进的路程是最短，该算法每次迭代时选择当前节点最近的子节点作为下一个节点[26]。同时在每一次迭代过程中，都要对源节点到所有遍历经过的节点之间的最短路径进行更新，最终得到最短路径。

在几十年的发展中，Dijkstra 算法显示出强悍的竞争力。因为实用性较高，该算法已经被多数研究者应用于实际程序中，例如谷歌地图[27]将此算法应用于自动驾驶导航之中。张瑜等[28]将Dijkstra的算法结合到一个动态窗口中，并对DWA中速度采样空间进行约束优化，用作未知环境中的路径规划，解决了清洗机器人加速过大导致的偏移量误差大的问题。韦荣杰等[29]深入研究了一种基于控制的移动机器人避障路径规划设计系统，并且做到了不需要繁重的计算量和不用占用较高的内存。Alshammrei 等[30]对Dijkstra 算法进行了改进，有效地解决包括障碍物在内的环境中的最优路径规划，但是路线的平滑度和连续性较一般。Durakli 等在文献[31]中的研究，结构更加简单，不需要添加任何中间节点，通过引入贝塞尔曲线修剪路径，使得路径更加平滑。此外，这种改进算法可以在动态环境中运行并检测到移动的障碍物，实时地更新路径。

为了进一步提高Dijkstra算法的性能，文献[32]采用Dijkstra 算法和蚁群算法混合并引入随机节点选择机制，文献[33]采用遗传算法优化Dijkstra算法的最短路径和投递顺序。这两种方法分别可以使其具有更好的全局搜索能力和更短的路径长度，但同时也增加了算法的复杂度和路径的复杂度。姜辰凯等[34]针对智能仓储中的路径规划问题将Dijkstra算法优化，进行时间窗排布，提出了一种路径长度更短，转弯角度更小的改进算法。此外，该算法还被广泛用于疏散线路规划[35]、铁路线路及船舶航线规划、物流调度等领域。改进Dijkstra 算法的文献对比如表1所示。

表1 Dijkstra算法改进分析Table 1 Improvement analysis of Dijkstra algorithm

总的来说，Dijkstra 由于其算法结构简单，收敛性好，所以在最优路径问题和疏散问题中的应用较广。从所引用的文献中可以发现，因为需要遍历更多的节点，导致计算量庞大，算法复杂度高，还会占用更大的内存，所以效率不高。

2.2 A*算法

A*搜索算法最早由斯坦福教授Nilsson 等[36]所发明。此算法基于Dijkstra 算法进行了深入研究，针对单个目标做了优化，算法的宗旨在于优先考虑似乎更接近目标的路径。A*算法与其他路径规划算法的最大区别在于启发式函数的组成[37]。启发式函数引导A*算法搜索最短路径，传统A*算法的启发式函数一般使用曼哈顿距离[38]、欧几里德距离[39]和切比雪夫[40（]对角线距离）。

Wang 等[41]提出了一种改进A*算法的路径规划方法，通过对启发式函数进行加权来提高计算效率，缩短处理时间，有效地解决了旅行商问题中的道路成本，但还存在着路径过长等局限性。Erke 等[42]提出了一种通过全局规划生成的准则，以开发启发式函数和变步长A*算法。与现有技术相比，所提的改进算法具有更好的鲁棒性和稳定性。熊旭等[43]应用了基于A*算法生成路径并使用贝塞尔曲线进行平滑处理，通过解决A*算法没有考虑车辆轮廓和缺乏速度规划的问题，保证了车辆的稳定性，同时也提高了A*算法在自动驾驶车辆规划中的适用性。郑涛等[44]在A*算法的代价函数中加入了角度评价代价函数，并利用跳点搜索的特性来提高搜索速度。

为了解决传统算法所存在的节点冗余问题，张燕等[45]介绍了路径二次规划的关键点选择策略，该策略删除了冗余的转弯节点和无效节点。付丽霞等[46]研究了不同障碍物尺度下网格路径规划的A*算法。同时，引入了改进的A*算法来优化关键点并简化关键点的路径。宋芮等[47]提出了一种改进算法，以解决传统A*算法受地图分辨率约束的问题。Wang等[48]使用开始目标代价函数对目标序列进行排序，并将改进的A*算法和动态窗口法相结合应用于多目标点规划。表2 是近几年部分改进策略的对比分析。

表2 A*算法改进分析Table 2 Improvement analysis of A* algorithm

可以看到A*算法作为经典的启发式算法，其计算效率较高，被广泛用于函数优化问题和设计优化问题。同时由于其启发式函数的鲁棒性较好，在最新的研究中通常被用于和其他算法的融合，进一步提高了算法性能。

2.3 快速随机搜索树算法（RRT）

快速随机搜索树（RRT）算法[49]是可以通过搜索可行路径步骤在所有引用的应用范围上应用于路径规划的几种技术之一。RRT 算法允许通过有效探索具有凸和非凸障碍的多维搜索空间来规划完整和非完整系统的路径。其操作包括从待规划路径的初始位置（根节点）扩展树形数据结构[50]，直到其一个树枝到达目标位置（最后一个叶节点）。

目前，基于RRT的算法已经被广泛地用于机器人路径规划[51]中。其中，对采样方式的改进是研究的热门。李柄辉等[52]提出了一种自适应双向搜索改进算法，可以很好地处理狭窄通道环境，同时保留RRT算法在其他环境中规划路径的能力。所提出的规划器被证明能够适应各种环境，并且可以在短时间内完成路径规划。康金谷等[53]提出了一种基于三角不等式的RRT-Connect 算法，利用三角不等式原理解决了RRT-Connect算法的寻优问题。所提出的算法在相似的样本数量和计划时间中显示出比RRT-Connect 算法更短的路径。Jeong 等[54]和廖兵等[55]同样引用了三角重新布线的思想，前者扩大了可能的父顶点集，并且使算法具有更好的初始解和收敛性，后者在加快收敛速度的同时显著降低了算法的成本。

Wang 等[56]将采样点进行聚类，随后在每个中心生成一棵树，最后使用强化学习来扩展这些树。Lai等[57-58]通过多个本地树来调整全局搜索状态。文献[58]还提出了使用贝叶斯估计来调整采样方向，来增强算法在复杂困难环境中的处理能力。这些改进算法通常根据空间信息计算并选择合适的树扩展方向并且具有很高的计算复杂度。此外，RRT 算法在自动泊车，自动驾驶以及物体跟踪行业有着广泛的应用。

从表3 中不难发现，最近的研究已经基本解决了RRT算法在狭窄通道中找不到解的问题，但是面对复杂环境时，其计算数据量大的局限性是有待克服的。

表3 RRT算法改进分析Table 3 Improvement analysis of RRT algorithm

2.4 遗传算法（GA）

遗传算法是由John H.Holland教授在著作《自然与人工系统中的适应》中提出的一种相对完整的理论和方法。此算法向达尔文的进化论学习，通过模拟自然进化的过程来构建人工系统的模型。GA利用计算机科学和自然生物遗传学来解决复杂的问题，主要涉及编码、初始化种群、适应度函数及值的计算、选择操作、交叉操作、突变操作。图3是遗传算法的简单流程。

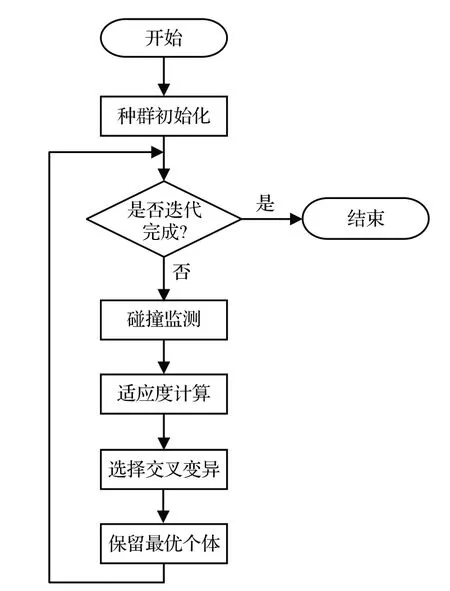
图3 遗传算法流程图Fig.3 Genetic algorithm flow chart

遗传算法具有简单、通用性强、鲁棒性强，适合并行处理的特点。作为启发式优化算法的典型代表，GA 的搜索策略和优化不依赖于问题的梯度信息。GA易于通过编程实现，并且该算法对优化问题的约束很少，可以轻松地使用它来修改现有的元启发式优化算法，以实现更好的性能。因此，GA 因其强大的全局优化能力和高效的并行性而在路径规划中得到广泛的应用[59]。

张昭君等[60]为了解决传统遗传算法随机初始化所导致可行个体的概率低和过早收敛问题，对初始化种群进行了改进，提出了一种具有混合初始化方法的新型遗传算法。该方法可以生成更好的初始种群同时通过删除和反向操作来提高算法的性能。同样在针对初始化种群的改进中，Lee 等[61]提出一种基于有向无环图的方法来提高算法性能；郝坤等[62]提出了基于多种群迁移的方法，将初始种群进行了连接，使离散路径连接到连续路径；李凯荣等[63]提出了随机搜索法和升序法相结合产生初始种群的方法来提升路径规划效率。而在适应度函数的改进方面，张铮等[64]提出一个改进的适应度函数，优化了自适应交叉变异操作，通过平衡阈值优化其性能来应用于动态环境规划；Lamin 等[65]提出了一种适合于遗传算法的适应度函数，通过减少其路径中的转弯次数以达到目标。遗传算子优化也是遗传算法的一个改进方向。张琼冰等[66]设计了一种新的交叉机制，该机制带有可变长度的交叉算子，成功提高了遗传算法的收敛速度；为了处理运动目标的问题，Patle 等[67]在此基础上提出了基于矩阵二进制编码的遗传算法（MGA），用于单机器人和多机器人系统的复杂环境中。在这种方法中，机器人可以很容易地跟踪移动障碍物和移动目标，并在短时间内到达目的地；Doostie 等[68]提出一种新的自适应遗传算法，采用A*算法寻找中间节点来拟合可行曲线，最后再引入邻域遗传算子。对于染色体长度的改进，倪建军等[69]提出了另一种新型遗传算法。在他们的方法中，染色体的长度被修改以获得最佳输出。GA方法对环境（已知和未知）做出了有效的反应；因此，它被用于水下机器人[70]和空中机器人[71]的三维路径规划问题，以及仿人机器人[72]的二维路径规划。表4 是遗传算法部分改进策略的对比分析。

表4 遗传算法改进分析Table 4 Improvement analysis of genetic algorithm

遗传算法虽然具有较强的路径搜索能力和较高的效率，在函数优化问题中展现出较强的竞争力，但其需要具体的经验，所以在面对未知环境时效果一般。

3 基于传感器信息的局部路径规划

局部路径规划一般属于在线（动态）的规划，移动机器人的内部传感器必须实时收集环境地图信息，确定地图和障碍的分布情况，从而选择从当前节点到目标节点的最佳路径。应用于此类问题的算法有：人工势场法、模拟退火算法、D*算法、蚁群算法、模糊推理法、强化学习法等。

3.1 人工势场法（APF）

1985 年，Khatib[73]提出了用于移动机器人导航的APF方法。根据他的观点，目标和障碍物就像带电的表面，总电势在机器人上产生了假想力。如图4所示，这个假想力将机器人吸引向目标，并使其远离障碍物。在这里，机器人沿着负的梯度，避开障碍物，到达目标点。人工势场算法结构简单，能够满足实时控制的要求。因此，该算法在处理动态避障路径规划方面还具有显著优势[74]。

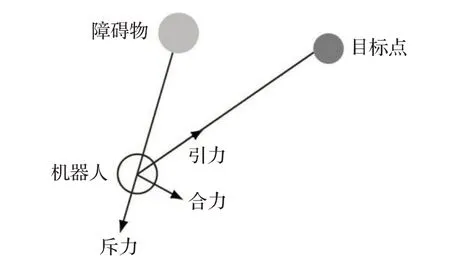
图4 人工势场法原理Fig.4 Principle of artificial potential field method

朱其丹等[75]在2006 年提出了一种无局部极小值的势场函数构造，能够针对特定环境而合理地逃逸局部极小值，从根本上解决了局部极小值问题。为了改进对环境的高要求，2017年，Abdalla等[76]提出了一种将人工势场法与模糊控制逻辑相结合的思想，放弃了具有局部最小问题的初始路径，直到传感器确认不存在碰撞风险为止。张成[77]将改进的人工势场方法与混沌优化算法相结合，解决了移动机器人在未知复杂环境中的摆动问题。王宏等[78]采用模型预测控制算法进行路径规划，将障碍物和潜在碰撞严重程度的人工电位场添加到控制目标中。王鹏伟等[79]提出了一种基于改进人工势场算法的避障设计。对人工势场方法进行了改进，重建了障碍物的排斥场范围，最后生成无碰撞路径。姚庆峰等[80]将人工势场方法改进为一种黑洞势场和强化学习相结合的方法，解决了局部稳定点的问题。林泽南等[81]基于APF方法提出了一种新的排斥场。将全局路径的长度和平滑度作为粒子群优化（PSO）的适应度函数，以获得APF中的障碍物影响范围、引力系数和排斥系数。Duhe等[82]提出了排斥场的四种替代公式：校正多项式、切向和径向分量、泊松势和伪分数势，有效地减少了移动机器人靠近障碍物时出现的振荡。

从表5中可以发现，人工势场法是局部路径规划中实用性较高的算法，在未知的环境中具有较强的避障能力。最近的研究通常是将人工势场算法和其他算法进行融合改进，在解决运动规划和避障问题中具有较好的鲁棒性。但是在规划时间和路径的最优问题方面，还需要进一步的研究改进。

表5 人工势场法改进分析Table 5 Improvement analysis of artificial potential field method

3.2 D＊算法

D*算法是基于A*算法的动态化改进，也是一种探路算法。它对路径的未被探索的部分进行假设，并基于这些假设找到从当前坐标到目标坐标的最短路径。随后机器人沿着这条路径移动，当它注意到新的障碍物信息时，它会把这些信息添加到地图上。在到达目标坐标之前，或在确定目标坐标无法到达之前，重复这一次过程。在穿越未知的地形时，往往会遇到新的障碍，因此，重新规划的过程需要更加快速。启发式搜索算法利用从以往问题中获得的经验，加速对现有问题的搜索，从而加快搜索类似问题的序列。

Stentz[83]最早在1995 年提出D*算法以用于火星探测器的动态避障。Drake 等[84]设计一种新的路径规划器，旨在追求移动目标。此规划器使用D*作为其初始路径查找的基础，然后从其搜索树中获取数据，以便在目标移动时快速重新规划路径。通过在搜索树中存储部分解路径，以加快当前搜索速度，而不会失去最优性保证。但是，所有这些算法都优化了一个目标：最小化沿计划路径的边缘成本值之和。但是在复杂未知的动态环境中，大尺寸区域处理始终是弱点，特别是在基于D*的路径规划中存在不必要的动态区域[85]。

在最新的研究中，许新宁等[86]通过自动分割聚类地图的方法，使用障碍物位置的信息来自动计算。俞建华等[87]针对位置环境的路径规划问题，将D*进行了改进，引入Dubins 算法进行局部路径平滑处理。孙兵等[88]在原有成本函数的基础上增加了障碍物成本项和转向角成本项作为约束条件，从而保证了导航的安全。任忠强等[89]提出一种在多目标增量搜索算法的基础上引入了MOPBD*的次优变体的改进策略，实现了比现有的多目标路径规划增量方法快一个数量级的优势。李孟泽等[90]设计了基于分散式边缘计算的系统架构，做到了可以实时更新地图信息，改进任务路径来进行重新规划。

表6是上述文献的改进分析对比。总的来说，D*算法虽然计算量大，路径不平滑，但是在处理动态障碍问题下，具有较强的可靠性，经常被用于未知环境的动态规划问题。

表6 D*算法改进分析Table 6 Improvement analysis of D* algorithm

3.3 模拟退火算法（SA）

模拟退火算法（simulated annealing，SA）最早是由Metropolis 提出的基于蒙特卡罗（Monte Carlo）思想设计的。1983 年，Kirkpatrick 等[91]将退火思想加入到优化领域，常用于在较大的解空间中搜索近似全局最优解的优化算法。

SA作为一种优化技术，可以处理具有非线性，不连续性和随机性程度的成本函数。它还可以处理强加给这些成本函数的任意边界条件和约束。Tavares 等[92]提出了路径的三种情况：折线、贝塞尔曲线、样条插值曲线。并且在所提出的SA 算法中，每次迭代时评估每个连续参数的灵敏度，增加接受的解的数量。每个参数的敏感性与它在下一个候选项的定义中的概率分布相关联。Ganeshmurthy 等[93]提出了一种将基于启发式的方法组合到基于模拟退火算法的方法中，用于动态机器人路径规划，通过组合启发式方法对运行时和离线路径规划进行了改进。孙琦等[94]通过启发式遗传算法降低模型在初始搜索路径中的随机性，然后结合Beam 搜索方法减少搜索所占用的空间和时间。苗辉等[95]开发了一种增强的SA 方法，该方法将两个额外的数学运算符和初始路径选择启发式方法集成到标准SA 中，用于移动机器人的动态路径规划。它显著提高了SA 的计算性能，同时提供了最佳的机器人路径解决方案，从而使其实时和在线应用成为可能。张琦等[96]将模拟退火（SA）和蚁群优化（ACO）算法相结合提出一种新的路径规划方法SAACO，用于解决未知环境下的移动机器人路径规划问题。翟龙镇等[97]将模拟退火和遗传算法结合，并且设计了自适应因子，避免搜索过程陷入局部最优解的同时，维持了种群的多样性。表7是改进模拟退火算法的分析对比。

表7 模拟退火算法改进分析Table 7 Improvement analysis of simulated annealing algorithm

3.4 模糊推理法

Zadeh 于1965 年最早提出模糊集的概念。在之后的研究中，Cordón等[98]用模糊逻辑算法表示从状态空间到控制空间的非线性映射。在路径规划中，先由模糊推理处理从传感器检测到的地图和障碍物信息，其次根据定义的模糊规则来进行模糊推理和决策。推理的结果被去模糊化以控制移动机器人的运动。对于采用模糊逻辑算法的避障[99]，通常将机器人与周围障碍物之间的感觉信息作为模糊控制器的输入，并为机器人输出新的移动指令。图5是模糊推理的流程。

图5 模糊推理过程Fig.5 Fuzzy reasoning process

为了更好地适应动态环境，宋琦等[100]将改进的蚁群算法与模糊逻辑方法整合到模糊逻辑蚁群优化（FLACO）中，提高了求解精度，节约了运算成本。Mirza[101]将模糊逻辑与神经网络结合，使它们在动态环境中具有强大的处理和适应能力。王宁等[102]和Lee[103]在解决水中航行器路径规划问题时，将人工势场法和模糊逻辑结合，克服了全局路径规划的缺点，有效的避免与障碍物发生碰撞。孙冰等[104]利用粒子群优化算法对模糊逻辑的隶属函数值进行优化，解决了路径规划中模糊逻辑的边界设计严重依赖专家经验的问题。Gharajeh 等[105]提出了一种基于自适应神经模糊推理系统，使移动机器人能够进行自主无碰撞，有效地找到不同场景下通过障碍物的无碰撞路径。王京华等[106]提出一种空间取点的优化方法，结合了Dijkstra 算法的原理。与图搜索算法相比，该算法大大减少了规划时间，提供了更灵活的转弯角度。与采样算法相比，该算法可以更好地考虑机器人的尺寸以及速度和转弯角度之间的关系，同时估计每一步的运动状态。表8是近几年对模糊算法进行改进的对比。

表8 模糊算法改进分析Table 8 Improvement analysis of fuzzy algorithm

3.5 蚁群算法（ACO）

蚁群算法（ant colony algorithm，ACO）是由意大利学者Dorigo[107]在1992年所提出。该算法是模仿蚂蚁寻找食物来源的行为[108]而衍生出的元启发式算法。蚁群算法因其并行处理、分布式计算和较强的鲁棒性，近年来被广泛应用到移动机器人路径规划领域[109]。图6 是蚁群优化原理的仿生示意图。

图6 蚁群寻找食物源Fig.6 Ant colony searching for food source

作为智能优化算法[110]的典型，蚁群算法在路径规划领域彰显了极强的竞争力。Utkarsh等[111]在网格地图中结合了移动机器人的定向运动和矢量运动，提出了一种快速的蚁群算法。王丽娜等[112]提出了一种改进的蚁群算法。通过引入Floyd 算法来生成引导路径，并增加引导路径上的信息素含量。通过初始信息素的差异，引导蚁群快速找到目标节点。其次，应用回退策略，减少因落入陷阱而死亡的蚂蚁数量，提高蚂蚁找到目标节点的概率。罗强等[113]提出一种改进的蚁群优化算法，构建分配不等的初始信息素和采用伪随机状态转换规则选择路径，解决了蚁群算法局部最优、收敛速度慢、搜索效率低的问题。Akka等[114]为了避免蚁群算法容易陷入局部最优解的缺陷，对信息素矩阵更新方法进行了优化。Uriol 等[115]分析并调整了ACO 算法的参数并且证明了ACO 算法在复杂环境下移动机器人路径规划的适用性。改进蚁群算法路径平滑度的方案也是研究的热门。戴晓林等[116]引入A*算法的求值函数和弯曲抑制算子，提高蚁群算法的启发式信息，加快收敛速度，增加全局路径的平滑度。杨辉等[117]提出了一种高效的双层蚁群优化算法，由两个独立连续运行的蚁群算法组成。首先，提出一种并行精英蚁群优化方法[118]，在复杂地图中生成初始无碰撞路径，其次应用一种称为转折点优化算法的路径改进算法，在长度、平滑度和安全性方面对初始路径进行优化。表9是改进蚁群算法的文献分析。

表9 蚁群算法改进分析Table 9 Improvement analysis of ant colony algorithm algorithm

3.6 强化学习法

随着智能科学的发展和人工智能的蓬勃发展，人工智能路径规划技术迅速成为专家学者研究的重点，而现有的一些路径规划算法采用许多静态策略，并且每个策略都与一个独立的环境实例进行长时间的交互，没有提出环境建模方法的判断。强化学习因为其无需建立路径规划问题的数学模型和环境图的特点，逐渐被用于协作解决避障、路径规划等问题。图7是强化学习的基本框架。

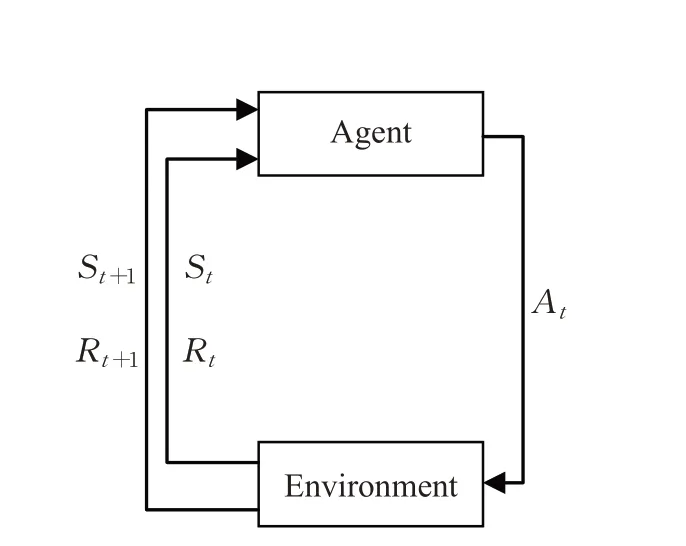
图7 强化学习的基本框架Fig.7 Basic framework of reinforcement learning

在求解路径规划问题的强化学习算法中，Q-learning算法是一种比较常用的与环境交互的学习方法。它是一种无模型的典型的强化学习方法[119-120]。这种方法不需要完整的环境知识。使机器人能够从环境中学习适当的行为，并在机器人路径规划中取得了良好的效果。Q-learning通过连续估计状态值函数和优化Q函数获得最优策略。Q-learning在一定程度上不同于普通的时差方法（TD）。它采用状态-动作对的Q(s,a)函数进行迭代计算。在智能体的学习过程中，需要检查相应行为是否合理，以确保最终结果收敛。

Bae等[121]将Q-learning和卷积神经网络（CNN）相结合，使移动机器人可以在各种环境中灵活高效地移动。Maw 等[122]提出了一种混合路径规划算法，该算法利用深度强化学习进行局部规划，使目标能够实时避免碰撞。ZENG等[123]将Q-learning算法应用于动态环境下的移动机器人导航，控制q值表大小，提高导航算法的速度。Low 等[124]引入部分引导Q-learning 的概念，初始化Q 表，加速Q 学习的收敛。Q-learning 算法也可用于求解基于网格图的路径规划问题。2010年，Bonny等[125]提出了一种扩展的Q-learning算法，通过引入标志变量，加快了Q函数的收敛速度，提高了算法的效率。

在近几年最新的研究中，Abdi 等[126]开发了一种结合计算机视觉、Q 学习和神经网络的新路径规划方法。Sahu等人[127]提出了一种创新的方法来解决移动机器人对在已知静态和复杂环境下的路径规划和同步问题，该问题解决了移动机器人从预定的起始位置到预设的目标位置的混合算法的设计，结合了改进Q-learning 的优点和粒子群优化[128]的特点（PSO）。Kim 等[129]利用Qlearning 对探索策略进行了调整，实现了实时路径规划。郭晓伟等[130]提出了一种改进的Q 学习算法来解决数字孪生装配系统中的移动机器人路径规划。

此外，Sarsa 算法是一种基于Q 学习算法的模型无关的强化学习方法。在移动机器人路径规划领域，Sarsa算法也可以与其他方法相结合。Asghari[131]等将Sarsa算法与遗传算法（GA）相结合来进行科学的调度分配。

表10 是强化学习算法改进策略的分析对比，作为智能优化算法的代表，强化学习算法体现了较强的实用性和适应性。对强化学习算法的改进可以在很多方向，总的来说，强化学习具有收敛快、时间短、路径优等优点，仍存在计算复杂的局限性。表11 是上述所有算法的对比。

表10 强化学习法改进分析Table 10 Improvement analysis of reinforcement learning

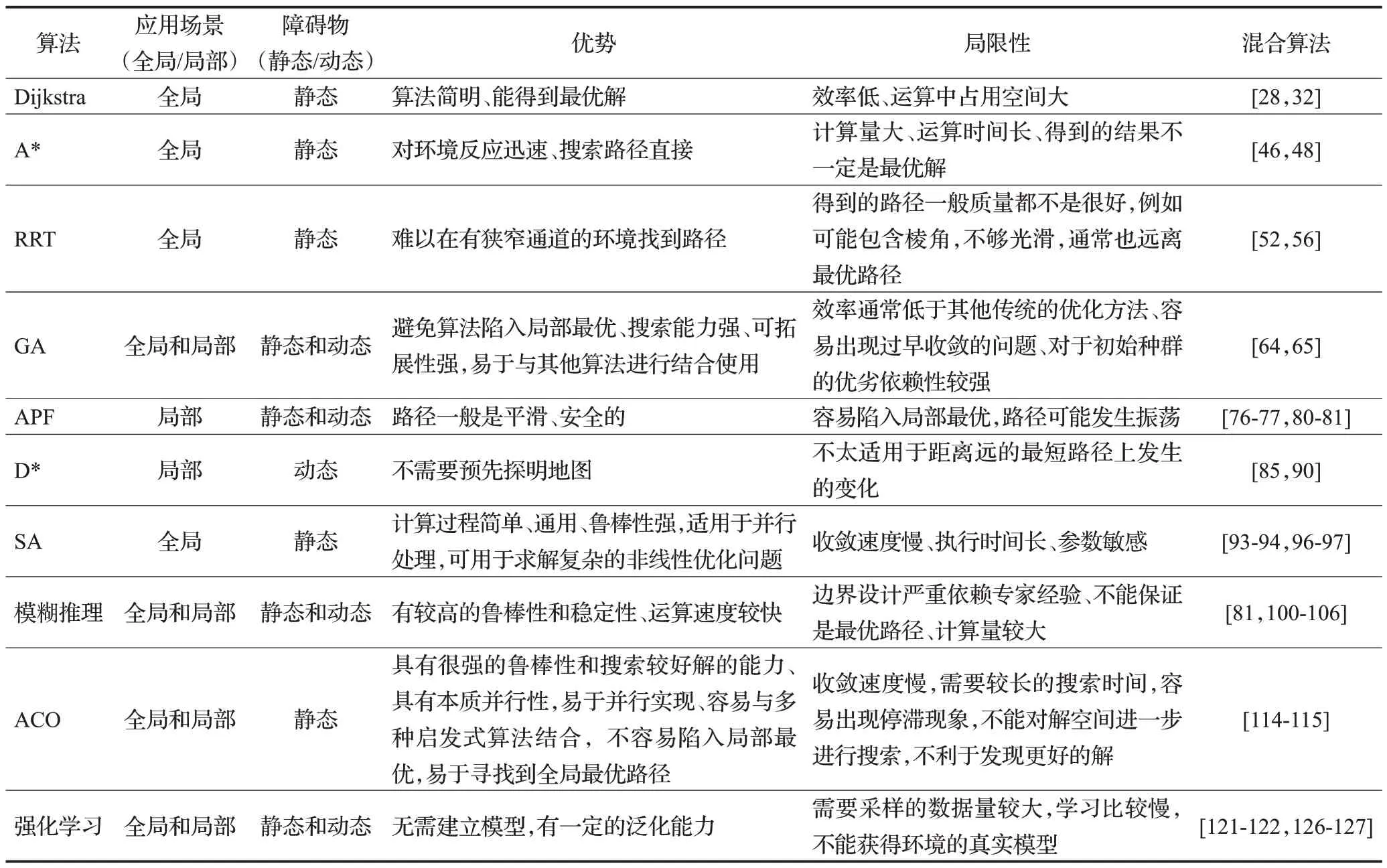
表11 所有算法的对比Table 11 Comparison of all algorithms

4 结束语

4.1 总结

本文将路径规划算法简单地分为两大类——全局和局部，综述了移动机器人路径规划技术的研究进展。此分类没有明确的界限，很多算法对于两种路径规划都适用。为了获得最优路径，针对不同的需求选择不同的路径规划算法尤为重要。文章针对不同算法进行了讨论和研究。其中，Dijkstra算法结构简单，但需要遍历更多的节点，因此效率不高。A*算法的关键是建立一个评估函数，以确保最短路径搜索始终沿着目标方向，这比Dijkstra算法的效率更高。适用于求解静态环境下的最短路径。RRT 算法适用于高维空间和复杂约束条件下的路径规划，路径生成的可行性可以满足要求。但是由于其随机采样的特性，往往规划时间较长。GA 因其在合适的参数下具有较强的路径搜索能力和较高的效率而被广泛应用，但参数的选择主要取决于经验，这对求解结果有很大影响。好的路径规划技术不仅可以节省大量时间，还可以减少人力和生产资源的投入。人工势场算法（APF）结构简单，能够满足实时控制的要求。因此，该算法在处理动态避障路径规划方面还具有显著优势。D*算法与A*相反，A*算法从起点到目标点进行搜索，而D*是从目标点向起点进行搜索进行反向传播，反向搜索。模拟退火算法（SA）作为一种优化技术，可以处理具有非线性、不连续性和随机性程度的成本函数。常用于在较大的解空间中搜索近似全局最优解的优化算法。模糊控制算法对于不确定性、随机性比较强的环境处理能力非常出众。能够适应多障碍复杂的环境，且可以安全避障，避障路径较为平滑。但是其对模糊控制器的专家经验要求较高。蚁群算法（ACO）具有并行处理、分布式计算和较强的鲁棒性，但是容易陷入局部最优，并且收敛速度慢和面对复杂环境搜索效率低。而强化学习算法的优势在于不需要完整的环境信息，能够让机器人从环境中学习适当的行为。但是一般来说，其计算复杂度较高，训练时间较长。

此外，与静态环境相比，基于动态环境发表的研究论文很少。而在动态环境中，针对移动目标问题的机器人路径规划研究较少，针对移动障碍问题的机器人路径规划研究较少。到目前为止，大多数论文只展示了模拟分析，关于实时应用的论文要少得多。与单一移动机器人系统相比，关于多个移动机器人系统导航的论文较少。与独立算法相比，关于混合算法的论文要少得多。

随着生产力的发展，路径规划技术也会逐渐变得高效和智能，在各个领域得到应用，与人们的生活息息相关。

4.2 发展趋势

随着计算机、传感器技术飞速发展，路径规划技术日新月异。在具体的路径规划算法中，都各自存在着优势和局限性。在今后的研究中，还需不断地跟进这些理论和实践。根据现在的发展状况，未来还可以在以下几个方面进行关注：

（1）新的混合方法

应用新开发的混合算法就是将路径规划的不同算法取长补短，进行有效结合。将路径规划的算法进行合理的结合能做到提高效率。很多方法如强化学习法[132]和模糊推理法[133]已经被应用到路径规划问题中。例如人工势场法和强化学习法的混合[134]可以有效地避免碰撞，使机器人快速、安全地到达目标点。将模糊算法和Dijkstra 算法混合[106]，可以再找到最优且平滑的路径。类似的这些混合式算法具有很大的发展前景。

（2）基础算法的改进

在现实场景中，路径规划过程都会面对许多挑战，尤其是例如收敛慢、计算量大的局限性，从而导致路径质量差、路径振荡等问题。而群体优化、蚁群优化、退火算法等受自然启发的方法可以为路径规划注入智能。需要新的仿真方法来集成动态环境中的机器人行为。此外，在机器人系统中，应该研究具有单位负载可达性约束的路径规划方法。因此在具体思想上进行改进，可以有效地提升算法的效率，解决路径规划中的问题。

（3）复杂环境的路径规划

移动机器人路径规划大多数解决了地面二维环境下智能机器人的路径规划研究，例如扫地机器人、服务机器人、安防巡检机器人等；而面向水下[135]和空中机器人的三维路径规划研究就相对较少。例如在水下机器人领域，许多特定的算法被提出用来解决水下环境的路径导航规划[136-137]，相比于二维模型更加复杂，需要考虑的影响因素也随之增加。

随着移动机器人技术的发展，路径规划的研究也将逐渐深入到复杂高维的地形环境中。此时就需要新的决策模型，机器人将在复杂环境中发挥至关重要的作用，需要新的方法来支持关于如何在复杂地图系统中规划和优化路径的决策。高维和复杂环境中移动机器人的路径规划是未来的一条必不可少的研究方向。

（4）多机器人路径规划

需要新的方法来进行多机器人路径规划，因为移动机器人正在进入新的环境并提供更多的服务。需要包括动态环境的不确定性（如交通、变化的行进路径和距离、区域内的变化的服务点和不同的服务活动）的方法来确定多机器人的协同。此外，需要找到多机器人的最佳比率的方法。仿真建模结合大数据、机器学习和预测分析可以支持这一点。此外，排队、流动和交通理论可以帮助分析整体避障，作为评估性能改善或降低的一个因素。在多机器人领域，多无人机编队路径规划[138]也是研究的热门方向，该研究不仅需要考虑多机器人，更需要考虑三维环境的避障问题。也是今后研究的重难点。