一种融合近似马尔科夫毯的随机森林优化算法

罗计根，熊玲珠，杜建强，聂 斌，熊旺平，李郅琴

1.江西中医药大学 计算机学院，南昌 330004

2.江西师范大学 信息化办公室，南昌 330022

随机森林（random forest，RF）[1]是集成分类模型，通过多棵决策树共同投票使模型具有高稳定性，同时也因其强大的分类能力使得它在各类数据挖掘比赛中脱颖而出，成为各家竞相追捧的算法之一。在恶意软件检测[2]、情境感知推荐[3]、疾病诊断[4]中有广泛的应用。

RF算法具有高准确率、泛化性强等诸多优势，但也存在不足。在遇到高维数据的时候，因其特征随机抽取机制，导致抽取的特征和类别变量相关性差，此外，随机抽取的自变量可能存在高度冗余，直接影响随机森林随机特征子集的质量，导致随机森林的收敛性减弱，降低随机森林模型的准确度、泛化能力及性能。因此，随机抽取的特征子集优劣是保证RF高准确率的前提。针对数据维度高，特征间高度冗余给随机森林模型带来的准确率不高的问题，本文提出一种融合近似马尔科夫毯的随机森林优化算法。

1 相关研究

针对随机森林模型随机抽取特征时所造成的自变量间存在相关性和冗余性等问题，Wu 等人[5]指出RF 算法，在特征子集选择时，会有大量不相关的特征进入特征子空间，从而影响分类器性能，提出一种分层采样特征子集空间的RF改进算法，分层采样的RF方法可以获得更高的分类正确率；姚登举[6]针对临床高维数据和特征间高度相关性等问题，提出在Filter 式特征选择基础上构建RF，先用RF 算法变量重要性对特征排序，然后通过迭代实验确定特征选择的阈值，选择特征重要性较大的特征构成RF的特征子集；针对高维特征冗余问题，姚登举等人还提出一种基于RF和序列联合搜索策略的Wrapper式特征选择算法，该算法利用RF善于从具有小边际效应和复杂相互作用的特征中识别主要相关特征的能力，以RF变量重要性分数作为特征重要性度量，采用序列后向和序列前向相结合的序列联合特征搜索策略选择特征子集，以特征子集上分类器的分类正确率评价特征子集的质量，最后选择分类正确率最高的特征子集作为最优特征子集；冯盼峰等人[7]提出两阶段逐步变量选择的随机森林算法，第一阶段提出变量重要性排序，目的是进一步提高重要变量与无关或者冗余变量的区分度，第二阶段完成随机森林的构建。

此外Amaratunga 等人[8]提出一种特殊RF 算法，该方法加权随机采样和特征排序方法提高RF 的分类性能，在10组真实的基因表达数据集上的实验表明，特殊RF 方法的分类性能优于基本的RF 方法；Svetnik 等人[9]通过交叉验证的方法计算数据每个特征的重要性评分并排序，重复20 次选取前50%的特征建立RF 模型；Genuer 等人[10]提出“两步法”构建RF 模型，第一步对特征降序排列，初步剔除不重要特征，第二步选择降序排列前K个变量，建立RF 算法，最终选择袋外数据验证误差最小的模型；同样Díaz-Uriarte 等人[11]提出建立RF判别模型，该方法通过计算特征重要性评分，不断剔除20%的变量，对剩余的特征建立RF判别模型，最后选择所含变量相对最少，分类精度最高的RF 模型。通过以上研究看出，现阶段对于高维样本构建RF 模型存在的特征相关性较差且存在冗余的问题，大部分研究集中剔除重要性偏低的属性，但会造成构建RF时，变量随机抽样存在多样性不高的情况，导致RF 的泛化能力不强的问题。

基于上述问题，本文在建立RF 算法随机抽取特征的多样性的基础上，消除特征相关和冗余特征的干扰，提出一种融合近似马尔科夫毯的随机森林优化算法AMBRF（random forest model combining with approximate Markov blanket），利用近似马尔科夫毯对原始特征构建相似特征组，得到不同的特征组合，决策树节点分裂前按照比例从每个相似特征组随机抽取一定比例的特征，得到最佳特征子集，完成决策树的构建，重复上述过程多次，达到随机森林规模，再根据改进的OOB测试方法得到最终模型评价结果。

2 随机森林

随机森林（RF）是一种经典的集成分类模算法，由多棵决策树（decision tree，DT）构成。RF对数据采取有放回随机抽样方法产生训练样本，假设数据集D的样本量为M，采用Bootstrap 有放回抽样时，单个样本被抽中的概率为1/M，通过抽取M次之后，单个样本没有被抽取到的概率为(1-1/M)M。只要样本量M足够大，数据集D会留下37%的样本未被抽中，这部分称为袋外数据（out of bag，OOB），用于模型评估。然后，训练样本采用随机抽样的方法抽取特征子集，特征抽取个数一般为,n为数据集D的特征个数。构建完多棵决策树后形成随机森林，通过对单个样本结果投票的方式得到测试样本的最终结果。随机森林算法的伪代码如下所示。

算法1随机森林（RF）算法

3 近似马尔科夫毯

针对RF 算法在高维数据集上表现出的不足，特征选择是有效解决办法之一。特征可以分为无关特征、弱相关且冗余、弱相关非冗余、强相关特四种[12]。好的特征选择方法则需要去无关、弱相关且冗余，保留弱相关非冗余、强相关特征。就近似马尔科夫毯[13（]approximate Markov blanket，AMB）方法给出如下定义：

设特征集合F、特征fi(fi∈F)、特征子集Mi⊂F(Mi≠fi)，分类的类别标签为C，概率为P。

定义1（强相关特征）特征fi是强相关特征时候，当且仅当[13]：

强相关特征是构建随机森林模型必不可少的，否则将影响数据分布。

定义2（弱相关特征）特征fi是弱相关特征时，当且仅当[14]：

定义3（无关特征）特征fi是无关特征当且仅当[14]：

最优特征子集不能包含无关特征。

定义4（马尔科夫毯）特征子集Mi是fi的马尔科夫毯[15]当且仅当在给定Mi条件下面特征fi和FMi-{fi}独立，即：

如果特征子集Mi是特征fi的马尔科夫毯，则fi一个特征即可表达特征子集Mi的全部信息，也包括特征子集Mi对类别C的表达，即当fi存在的时候，形成的Mi对分类没有贡献能力，可以选择丢弃，视Mi为fi的冗余特征，强相关特征是不存在马尔科夫毯。

定义5（近似马尔科夫毯）特征fi是特征fj的近似马尔科夫毯[16]的条件为：

其中，表达式J(fi,C)表示特征fi和类别C的相关性，J(fi,fj)表示fi和fj的相关性，本文中使用J(·)选择最大信息系数[17（]maximal information coefficient，MIC）计算，如公式（1）所示：

其中，D={(f1i,f2i),i=1,2,…,n} 是有序对集合，X表示将f1的值域划为X段，Y表示将f2的值域划分为Y段，XY ＜B(n)表示网格数目不大于B(n)，分子I*(D,X,Y)表示不同X×Y网格划分下的互信息最大值，分母ln(min(X,Y))表示将不同划分下最大互信息归一化的值。MIC(D)∈[0,1]，越接近1 表示两者相关性越高，反之相关性越低。

定义6（相似特征）特征fj是fi特征的相似特征[18]的条件是：fi是fj的近似马尔科夫毯。

fi和fj拥有相似的信息，都是对类别标签的同一部分信息进行表达。

定义7（相似特征组）相似特征组是近似马尔科夫毯fi和fj的所有相似特征的集合。

为了使得RF算法在随机抽取到的特征与类别C具有相关性且满足RF算法特征多样性的要求，利用AMB构造相似特征组。算法伪代码如下所示。

算法2基于近似马尔科夫毯的相似特征组聚类算法

4 融合近似马尔科夫毯的随机森林模型

RF 算法强大的分类能力离不开两个随机，随机之一即为特征随机抽取，RF在处理高维样本时，极有可能抽到大部分特征都是无关特征或者弱相关冗余特征，将造成RF算法精度降低，泛化能力减小。AMB算法可有效地将相关特征聚类，形成相似特征组，即在相似特征组中，随意抽取一定比例特征fi可代表该整组特征的全部信息，也可以包含对分类标签C的表达。融合近似马尔科夫毯的随机森林模型先利用AMB算法构造相似特征组G={G1,G2,…,Gp}，再根据特征比例从每组特征Gi随机抽取特征构造RF算法单棵决策树的划分属性。该模型构造流程如图1所示。

图1融合近似马尔科夫毯的随机森林模型（AMBRF）流程图，输入样本的特征维度是n，根据文献[19]，单个决策树分裂属性个数定为，由AMB 算法得到p相似特征组，其中相似特征组Gi包含xi个特征，则按照比例应从该相似特征组Gi中随机抽取个属性，按照同样的思想从其他相似特征组中抽取部分属性，构建单棵决策树。重复上述过程多次，直到满足随机森林规模后停止构树。融合近似马尔科夫毯的随机森林（AMBRF）算法伪代码如下所示。

算法3融合近似马尔科夫毯的随机森林算法

当样本数量m足够大的时候，理想情况下总会留下约37%的样本抽不到而成为OOB 数据，但是现实中样本有限，如果以OOB数据作为测试样本，存在测试样本不足的情况。因此对随机森林的精确测试上，改变传统OOB 测试的方法，提出样本单棵决策树轮空测试法进行实验验证。具体思想为：遍历所有样本，取到样本i之后，遍历RF中所有决策树，如果样本i不作为第j棵决策树的训练样本，则进行测试，得到该样本的预测标签，直到所有决策树预测完之后，投票表决样本i的类别标签，直至所有样本验证完成结束算法。

假设训练集样本个数为m，构建为k棵CART决策树，特征数为n,原始随机森林的时间复杂度为O(kmn(logm)2)[20]。本文提出的AMBRF算法共分成两部分：构建近似马尔科夫毯相似特征组和建立随机森林模型。对于第一部分，其时间主要花在计算两个特征之间的相关性MIC值，时间复杂度为O(m2.4)[21]，因此本部分的时间复杂度为O(nm2.4)，第二部分为随机森林构建，设此阶段需要从p个相似特征组中抽取部分特征，时间复杂度为O(kpmn(logm)2)，综上可知，本文提出AMBRF算法的时间复杂度为两部分之和，即O(nm2.4+kpmn(logm)2)。

5 实验结果及分析

5.1 实验数据

为了客观且全面地验证本文提出的融合近似马尔科夫毯的随机森林模型（AMBRF）的优势，分析AMBRF在不同特征维度的数据集适应性，选取UCI上12 组不同维度的数据集，表1为12组数据集的基本信息。

表1 UCI数据集Table 1 UCIdata set

5.2 评价指标

本文提供的模型评价指标有准确率（Accuracy）、精确率（Precision）、召回率（Recall）、F 值，依据表2 所示的混淆矩阵，可以得到这些评价指标的计算公式：

表2 混淆矩阵Table 2 Confusion matrix

为全面评价本文提出的AMBRF算法，从近似马尔科夫毯构建相似特征组时间、特征相关性的误差平方和、AMBRF 和其他分类算法各类评价指标等角度分析本文实验。

5.3 实验结果及分析

本实验设备采用Intel®CoreTMi7-10510U CPU @2.30 GHz，RAM 16.0 GB，64 位Windows10 操作系统，对以上12组实验数据，共设置3组对比实验，就以上4个评价指标进行对比分析。

实验一为构建基于近似马尔科夫毯的相似特征组所耗时间和均方根误差RMSE分析，实验结果见表3所示。

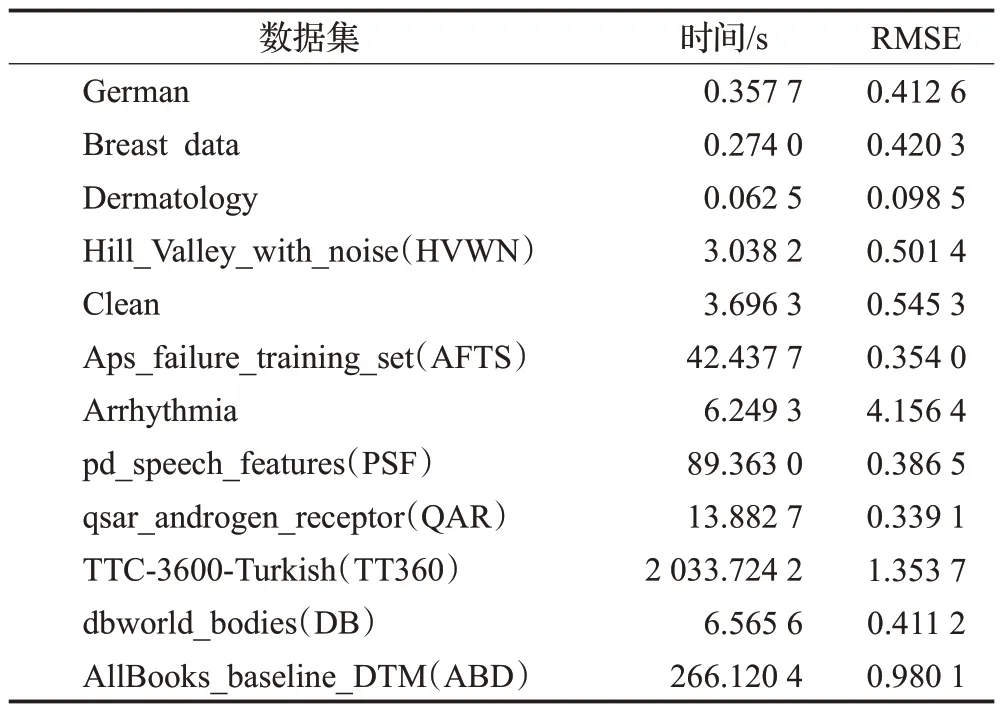
表3 构建基于AMB的相似特征组所耗时间和RMSE分析Table 3 Time and RMSE analysis of building AMB based feature similarity groups

由表3 的实验结果可知，RMSE 在各组数据上均保持在较低的水平，表明构建基于AMB 的相似特征组和因变量的相关性较大，能很好地反映各个相似特征组对因变量的表达具有较高的全面性。

结合表1的数据信息内容和表3的实验数据可以看出，构建基于AMB 的相似特征组所耗时间跟样本数量和特征数量存在明显的关系，TT3600 数据集的样本量达到3 600条，特征数量达4 813个，是12个数据集中规模最大，因此在构建该数据集的相似特征组所耗时间为2 033.724 2 s。AFTS数据的样本量虽然达到60 000条，但是因为其特征个数只有170个，因此所构建的相似特征组就少，耗费时间较少，只要42.437 7 s。

实验二为RF和AMBRF以及文献[22]利用Fisher系数对特征排序，再按组随机抽取特征的FisherRF三组算法的各种评价指标对比实验，表4即对比实验的结果。

表4 RF和AMBRF算法的准确性对比实验Table 4 Accuracy comparison test of RF and AMBRF algorithms

为了直观地展示三个算法在12 组数据中的效果，绘制如图2所示的柱状图。

图2 各组数据集对比实验柱状图Fig.2 Comparison test histogram for each data set

根据表4和图2所示，RF和FisherRF、AMBRF在各组数据上的对比实验结果可以看出，AMBRF 在高维数据中各项评价指标上均有明显的提升，具体分析如下：

（1）在German、breast_data、dermatology、HVWN 四组低维数据集上，AMBRF算法各项指标均不如传统RF和文献方法FisherRF，但是三种算法在综合指标F 值上相差不大，甚至接近。因为四组数据的维度相对较低，均在100 维以下，特征之间的冗余度不高，特征之间却存在不相关性，所以FisherRF 更加适宜于这种情况，由实验结果也可反映出这种问题。而AMBRF 算法在构建基于AMB 的相似特征组时，由于需要从每个特征组合中随机抽取一定比例的特征个数，这将导致构建每棵树的特征多样性减少，使得AMBRF算法的决策树多样性减弱，导致整个模型的效果偏低。

（2）对于Clean、AFTS、Arrhythmia、PSF 数据中，特征维度在100到1 000之间，这四组数据中，本文提出的AMBRF 和文献FisherRF 各有所长。在Clean、AFTS 这两组数据中，AMBRF 的各项评价指标高于FisherRF 算法；在Arrhythmia、PSF 这两组数据中，FisherRF 的各项评价指标高于AMBRF算法；为了验证在特征维度适中情况下，AMBRF 和FisherRF 算法的优劣性，设置AMB构建相似组对比实验，根据相似组个数、每个相似组的特征个数等角度解释造成上述现象的原因。

如表5 所示，通过查看每个相似特征组的特征个数，以及每个数据集构建的相似组个数可知，Clean数据集的每个相似组中均有多个属性，特征间的冗余性较大，同理AFTS数据集的每个相似组也存在这种特征之间冗余性较大的情况。但在Arrhythmia、PSF 两组数据上，构建的相似组更多，存在多个相似组只有1 个特征的情况（Arrhythmia数据集构建了18个特征组均只含有1个特征，PSF数据集构建了6个特征组均只含有1个特征，而Clean和AFTS两组数据集都只存在1个相似组含有1个特征，相似组内特征越少冗余性越低），根据算法3可知，从这些相似特征组中抽取的特征子集较为单一，多样性不高。相比于Clean和AFTS数据集，Arrhythmia、PSF 数据集特征维度较高，但是特征间的冗余性不大。综上分析，AMBRF 更加适用于存在大量冗余特征的数据集，对特征存在高度冗余的数据集有更好的效果，也可反映出文献算法FisherRF 可以解决特征无关特征对随机森林构建的干扰，对特征冗余性较高的数据集效果不明显。

表5 AMB构建相似组对比实验详情Table 5 Details of comparative experiment of similar groups constructed by AMB

（3）在剩下的4 组数据中，ABD 数据的特征个数达到8 266 维，其余三组数据QAR、TT3600、DB 也都超过1 000维，此时改进算法AMBRF的效果明显优于FisherRF和传统RF。在数据集QAR 上，改进算法AMBRF 的综合评价指标F 值为0.826 0，传统RF 的F 值为0.665 2，FisherRF 的F 值0.815 3，均有所提升；在数据集TT3600上，AMBRF 的综合评价指标F 值为0.708 5，传统RF 的F 值只有0.295 8，FisherRF 的F 值仅为0.390 2。在这组数据集上，AMBRF相较其他算法提升幅度达到31%；在数据集DB 上，改进算法AMBRF 的综合评价指标F 值为0.938 5，传统RF 的F 值为0.760 1，FisherRF 的F 值为0.845 6，AMBRF 相较其他算法提升幅度达到9%；数据集ABD 上，改进算法AMBRF 的综合评价指标F 值为0.739 3，传统RF 的F 值只有0.359 7，FisherRF 的F 值为0.550 8，AMBRF 相较其他算法提升幅度达到19%。通过上述分析知道，AMBRF 算法在TT3600、ABD 两组数据集上表现异常突出，究其数据特点可知，这两组数据均为文本分类任务构建的词袋模型，特征维度较高且稀疏，存在大量的冗余特征，因此通过随机抽取相似特征组中特征可以有效避免传统RF随机抽取特征形成冗余特征子集。

综上所述，本文提出的AMBRF算法相比于其他两种算法具有更好的实验效果，尤其是对高维数据，或者是存在高度冗余特征的数据中具有明显的优势。

实验三为RF、FisherRF和AMBRF三组算法随机森林构建时间对比实验（不包括相似特征组构建时间），表6展示三个算法对比实验的结果。

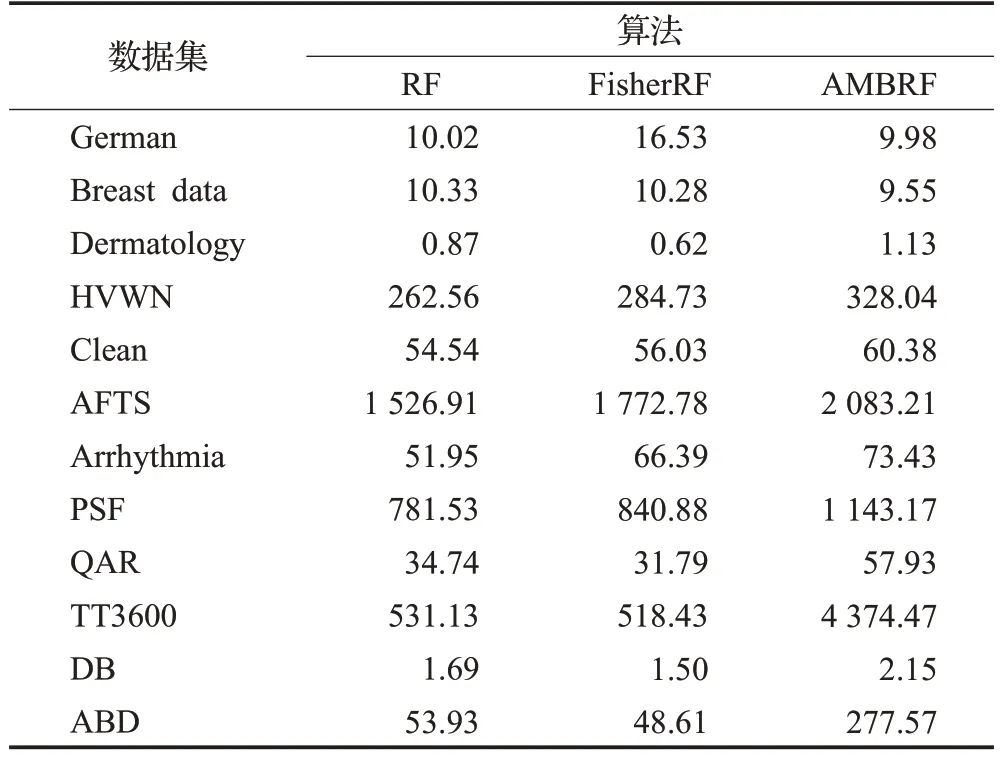
表6 构建随机森林的时间对比实验Table 6 Time comparison test of constructing random forest 单位：s

由表6 可知，当特征维度比较低时，RF、FisherRF、AMBRF 三种算法在构建随机森林消耗时间更加接近。特征维度较高时，RF 和FisherRF 在构建森林时所耗时间整体上低于改进算法AMBRF 构建森林的时间。这是因为使用AMBRF构建随机森林的时候，要求先构建相似特征组，构建单棵决策树的时候需要遍历所有的相似组特征，按比例从其中抽取部分特征，合成最优特征子集，因此构建100 棵树时，需要重复上述循环100 次，导致改进算法AMBRF 在建立随机森林时耗费的时间比其他两种算法更长。由AMBRF 的时间复杂度O(nm2.4+kpmn(logm)2)可知，耗时的长短主要由样本数量m决定，当样本量较大时，构建随机森林消耗时间更长，由TT3600 数据集的时间对比实验可以明显看出，AMBRF构建随机森林时间为4 374.47 s，是其他两种算法的8 倍，从实验角度验证本文分析的AMBRF 算法时间复杂度的正确性。

6 总结

针对特征的相关和冗余，影响随机森林（RF）随机抽取特征的质量等问题。本文提出一种融合近似马尔科夫毯（AMB）的随机森林算法（AMBRF），该算法先利用AMB 构建多个相似特征组；再从每个相似组中按照比例抽取特征形成单棵决策树的最佳特征子集，重复上述过程多次。该算法利用AMB消除特征间的相关性和冗余性，提高随机抽取特征的质量。通过大量验证性实验得出本文提出的改进算法AMBRF优于传统RF算法及FisherRF算法，对高维样本和具有冗余特征的样本更加切实可行。但是，对于特征数较少的数据集会增加各决策树之间的相关性，使决策树不具备多样性，效果不佳；AMBRF 构建随机森林的复杂度明显高于其他两种算法，使得运行时间较大；在今后的工作中，将重点考虑这两个问题。