多维Star-QAM星座优化的SCMA码本

张 丽

（西华大学理学院，成都 610039）

0 引言

随着物联网（IoT）和大规模机式通信（mMTC）设备［1］应用的快速扩展，支持依赖于第四代（4G）长期演进（LTE）［2］继承的物理层解决方案的通信设备具有挑战性。由于第5 代（5G）和第6 代（6G）通信中频谱稀少且拥挤，正交多址（OMA）可能不适用于物联网应用的要求。为了实现更高层次的连通性和频谱效率［3］，非正交多址技术（NOMA）被认为是一种很有前途的技术。因此，提出了非正交多址技术之一的稀疏码多址（SCMA）［4］。

与通过预先分配的资源元素（REs）重复传输特定星座的低密度签名（LDS）方案相比，SCMA方案将信息位映射到在预先分配的REs［5］上的多维星座，以最大限度地提高码字对的最小欧氏距离。因此，SCMA 具有更好的符号映射多样性增益［6］。同时，受益于组合调制和扩展过程［7］，SCMA以更高的系统复杂度为代价，获得了比其他的CD-NOMA 技术更好的误差性能，因此SCMA码本的设计尤为重要。

如今，码本的设计仍然是一个开放性的问题，目前已经有多种次优码本的设计，但是并未有最优的码本。Liu 等［8］提出了一种将上行无线通信的稀疏码多交调幅（QAM）划分为多个子集，实现优化后的稀疏码多址（SCMA）码本的优化设计。Mheich 等［9］使用黄金角调制（GAM）点来构造上行和下行稀疏码多址（SCMA）系统的码本，在下行链路中，使用GAM 的点集为SCMA码本构建一个多维母星座，而在上行链路中，GAM 的点集被直接映射到用户码本。Zhang等［10］提出了一种构造下行稀疏码多址（SCMA）系统码本的方法，每个子信道的码本都是基于最常用的QAM 调制的，同时用低误差概率准则来衡量信道在高斯信道和瑞利衰落信道中的SCMA码本性能。Li 等［11］提出了一种新的 SCMA 码本，它展示了不同用户之间的功率不平衡的下行传输，基于Star-QAM 母星座结构，并借助遗传算法，对所提出的码本的最小欧氏距离（MED）和最小乘积距离（MPD）进行了优化。Yu 等［12］提出了一种基于星形正交振幅调制（Star-QAM）信号星座的SCMA码本设计方法。基于四环Star-QAM信号星座的MC 设计方案，验证当内半径之比为0.63且内外半径之比为1/3时，码本性能最优。

本文在四环Star-QAM 信号星座上，再增加了一组内外圆环，同时将三组内外半径比设置为1/3，外部半径加入旋转参数，三组内半径为尺寸优化参数，利用多目标粒子群优化算法（MOPSO）［13］，最大化最小欧氏距离（MED）和最小乘积距离（MPD），从而求解出相关参数构造用户码本。仿真结果表明该码本较之前码本相比误码率得到一定控制。

1 SCMA系统介绍与码本设计

1.1 SSCCMMAA系统介绍

考虑一个下行链路SCMA 系统，其中基站发射机同时与共享K个资源节点的J个用户进行通信，定义系统的过载因子λ=(JK) ＞ 1。不同于低密度签名（LDS），映射器和扩展程序在SCMA 中被合并在一起，一个SCMA 编码器直接将输入的log2M位比特流映射到一个大小为M的K维复数星座X，然后叠加J个用户的码字进行传输。在接收端接收到的信号向量y=(y1,y2,…,yK)T可以表示为

其中：h=(h1,h2,…,hK)T表示发射机到用户的信道向量，且满足hk～CN(0,1)，diag(.)表示对角化向量，xj=(x1,j,x2,j,…,xK,j)T表示从码本Xj中选择的用户j的K维复数码字，其中1 ≤j≤J。n=(n1,n2,…,nK)T表示均值为零和方差为δ2IK加性高斯白噪声（AWGN）向量［14］。

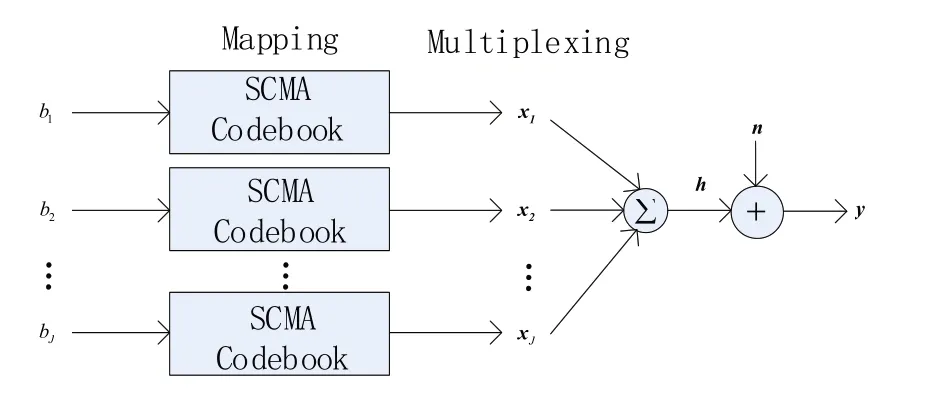
图1 SCMA下行链路模型图

1.2 码本设计

在SCMA 信号的发送端，SCMA 编码器执行将q=log2M编码位的信息映射为大小为M的K维复数码本，该定义为

其中：b表示输入信道编码比特，x∈X⊂Ck是一个K维复数码字的稀疏向量，其中||X||=M。

本文通过直接构造子星座来获得SCMA 用户码本，具体步骤如下：

（1）构造子星座S1,S2,S3,大小均为1 ×M；

（2）根据因子图矩阵FK×J将S1,S2,S3分配到因子图矩阵的非零元素位置，将大小与子星座相同的零向量分配到因子图的零元素位置，从而获得用户码本。

1.3 最小欧氏距离和最小乘积距离

在SCMA 系统中，J个用户的码本在K个资源块上同时传输形成叠加码字，构成有MJ个叠加码字的叠加星座V。最小欧氏距离Emin是MJ个叠加码字之间MJ(MJ-1)种距离中的最小值，它是高斯信道下误码率性能的关键指标，可表示为

其中第n个叠加码字x(n)表示为

在瑞利衰落信道下，最小乘积距离Pmin是主要的性能指标。计算包含所有J个用户码本的Pmin如下：

2 下行瑞利衰落信道下SCMA 的码本设计及优化

2.1 SSCCMMAA码本设计

在本文中，首先参照文献［12］中的结论，将三组内外环半径比值设置为13，构造三个子向量a1=(-3*R1,-R1,R1,3*R1)，a2=(-3*R2,-R2,R2,3*R2)，a3=(-3,-1,1,3)。其次对三个子向量的外环引入旋转参数，增加自由度，三个子向量表示为A1=(-3*R1*b0,-R1,3*R1*b0)，A2=(-3*R2*b0,-R2,R2,3*R2*b0)，A3=(-3*b0,-1,1,3*b0)，其 中b0=ei*2*π*α。再 对A1,A2,A3各自进行整体的旋转操作形成三个子星座S1=b1*A1，S2=b2*A2，S3=b3*A3，其 中b1=最后，根据因子图矩阵F确定非零向量和零向量的位置，根据签名矩阵S确定三个子星座的分配，本文的因子图矩阵F、签名矩阵S和文献［11］中的因子图矩阵、签名矩阵相同。为了降低码本的平均峰值功率比（PAPR），对用户码本按照文献［15］的规则进行交织操作。本文的资源块数量为4，用户数量为6，用户码本大小为4 × 4，则用户1的码本可表示为

类似地，我们能获得其余的用户码本。

2.2 下行瑞利衰落信道下码本优化

在下行瑞利衰落信道下，以最大化最小欧氏距离Emin和最小乘积距离Pmin为优化目标，优化函数如下：

最终根据多目标的粒子群优化算法得出结果，如图2所示。

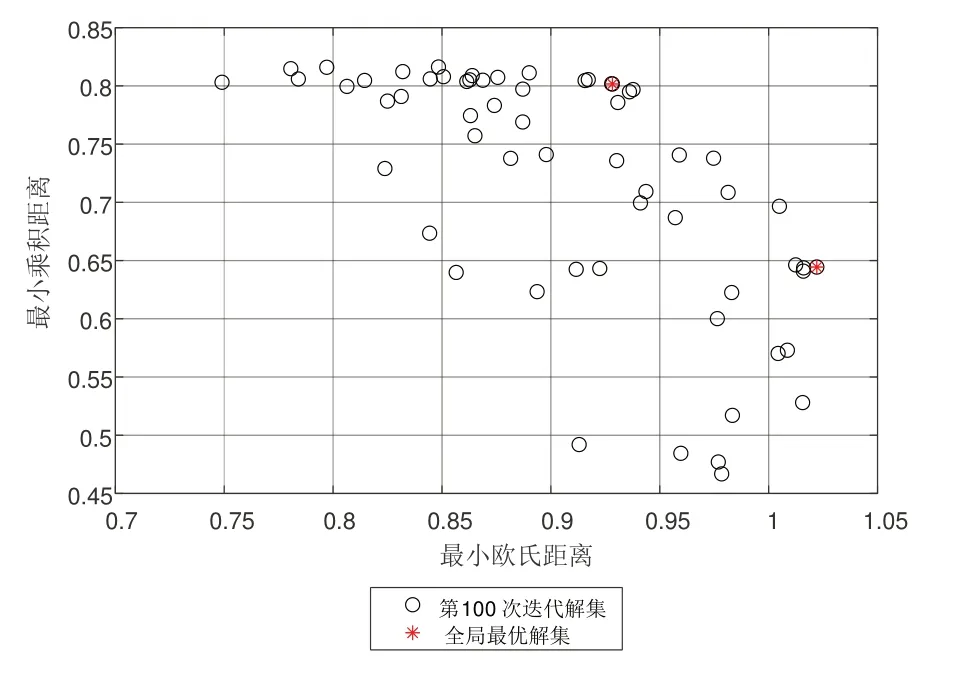
图2 下行瑞利信道下粒子群算法优化图

通过图2 可知，经过100 次迭代之后，精英库中有两组帕累托（Pareto）解［13］。这两组解则构成全局最优解集，最优解有相应的目标函数值。

3 仿真结果

本文对多维星形正交振幅调制星座优化的SCMA 码本进行参数优化，将其命名为Prop 码本。将 Prop 码本与 Star-QAM 码本［12］、DEMC 码本［16］进行比较，为了便于比较，将三种码本的平均能量都定为1，具体情况见表1。考虑多维圆环半径设计标准，Pareto 解2 的半径参数太过于接近，不符合设计要求，因此舍去，最终选取 Pareto 解 1（R1=1.35,R2=1.50,θ1=0.30,θ2=0.58,θ3=0.85,α=0.03）作为目标解。

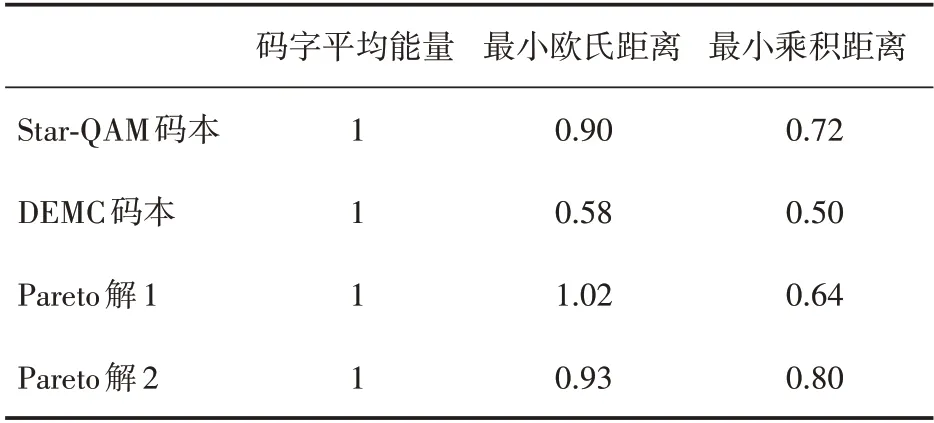
表1 不同码本比较

在高斯信道和下行瑞利衰落信道下，对Prop 码本与 Star-QAM 码本、DEMC 码本进行BER 性能优劣比较，相关的仿真参数见表2。根据图3 的仿真结果所示，在高斯信道下，当BER=1e-4 时，Prop码本相比 Star-QAM码本有1 db 性能增益，相比于DEMC 码本有3 db 性能增益。在下行瑞利衰落信道下，当BER=1e-3 时，Prop 码本相比 Star-QAM 码本、DEMC码本分别有0.5 db和5 db的性能增益。

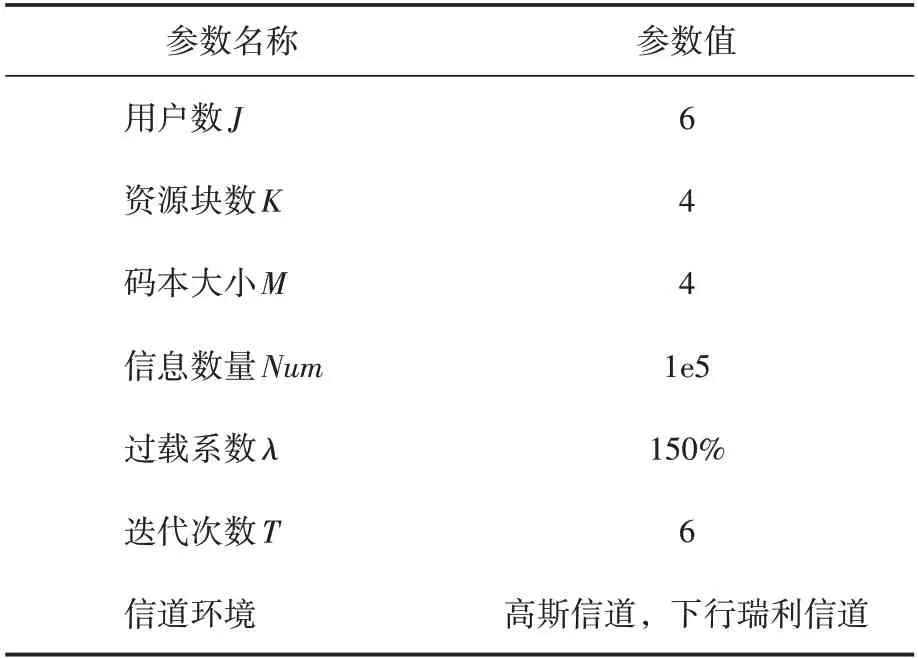
表2 码本仿真参数

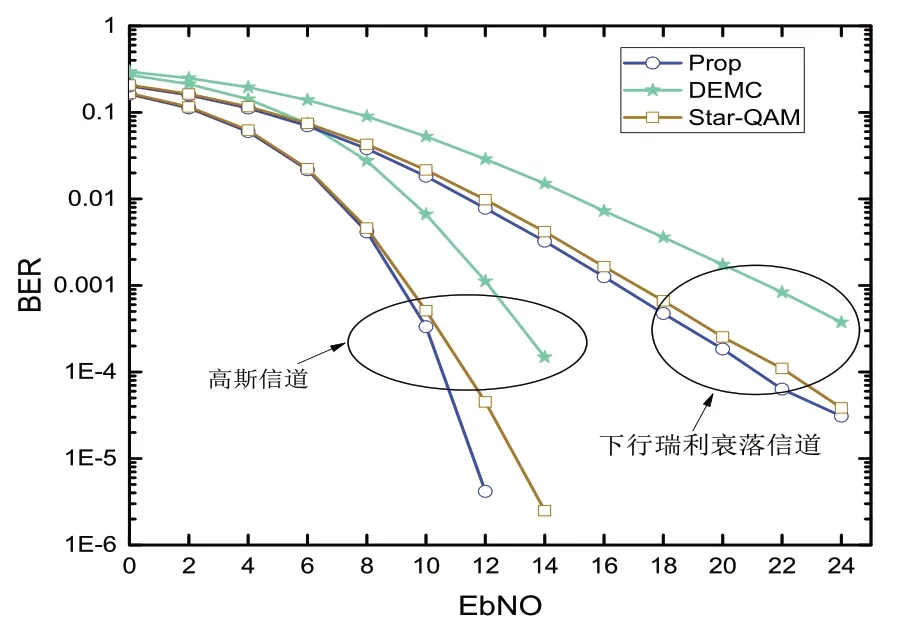
图3 码本误码率比较

4 结语

本文提出的多维Star-QAM 星座SCMA 码本设计，通过引入新的半径参数、外环旋转算子参数以及子向量的旋转算子参数，增加自由度。再以最大化最小欧式距离和最小乘积距离为目标函数，在多目标粒子群优化算法的帮助下，找出符合要求的目标解，从而求出用户码本。仿真结果显示，本文构造的码本在误码率性能上相比之前的码本有所提高。