神经网络技术在电气自动化设备故障诊断中的应用

芦小雨 程 刚

（中国电建集团河南省电力勘测设计院有限公司，河南 郑州 450000）

1 神经网络技术原理

神经网络的基本原理就是将多个不同神经元的计算机单位层级进行连接权重的相互连接，进而构建信息处理数学模型。神经网络内部包括一个输入层、多个隐藏层和一个输出层组成，输入层接收外部指令信息，输出层产生最终的预测结果或输出，隐藏层位于2 层之间，每个隐藏层内包括多个神经元。通过前向传播手段将上、下神经元进行连接，神经网络中处理信息随层次依次向下层传递，再采用激活函数来确定神经元的输出。但是学习连接权重与信息处理传递流程相反，通过反向传播手段将输出层信息传播到隐藏层和输入层，训练和调节连接权重，基于损失函数来度量预测结果与真实标签之间的误差，最后根据梯度更新连接权重，起到降低误差的作用。另外，神经网络可以有效识别输入数据的特性，进而完成数据分类、预测等任务[1]。神经网络结构示意图如图1所示。

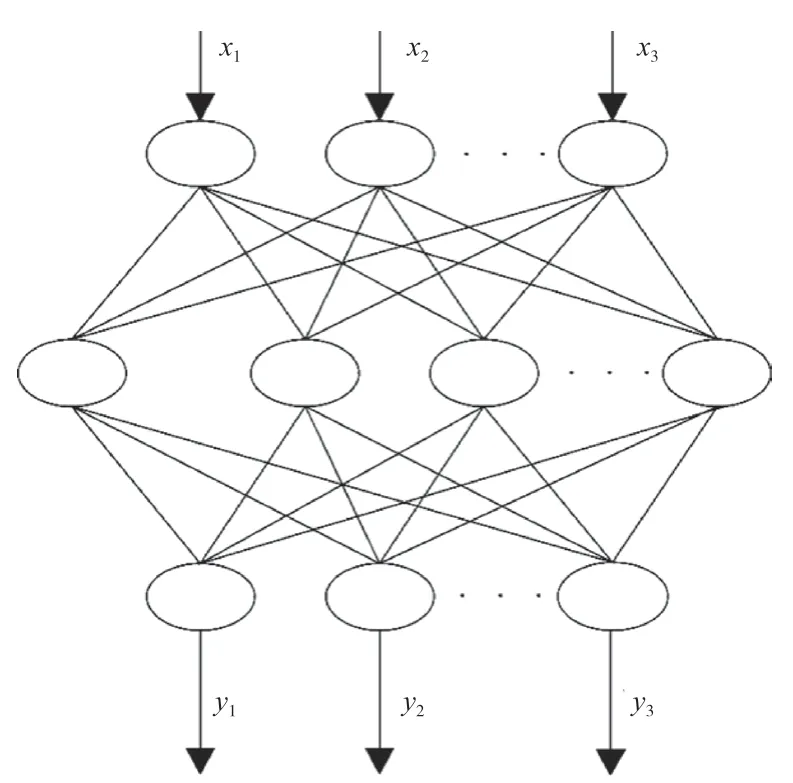
图1 神经网络结构示意图

神经网络应用主要包括前向计算、平均误差计算及误差反向传递3 个部分，具体内容如下。

1.1 前向计算

进行前向计算时，先在神经网络内输入选定的采样点数据，并将采样点负载端输出的原始数据On视为各输入层节点的输出点，其表达式如公式（1）所示。输出层输入则用Im表示，其表达式如公式（2）所示。隐层输入用Ij表示，其表达式如公式（3）所示。

式中：On为输出层第n个节点输出；Xn为输入层第n个节点输出；n、N代表各输出点；Im为输出层输入；Vi，j为自隐层至输出层的连接权重；j为隐层输入；H为函数系数；Ij为隐层输入；Wi，j为自输入层至隐层的连接权重；an、aj为相应的阈值。

通过上述公式可融合得出相应节点输出的非线性函数。

1.2 计算平均误差

计算平均误差时，常用E表示和计算所有样本的平均误差，如公式（4）所示。

式中：E为训练结束判断参数；k为训练样本；N为训练样本个数；M为输出神经元的个数；Ek为第k个训练样本的平均误差；ekm为第k个样本的输出神经元m的误差。

1.3 误差反向传递

误差反向传递是利用网络中权系数与输入训练样本次数之间的密切关系，对网络中的权系数进行反向调整的过程。具体计算时，先通过公式（5）对输出层与隐层之间的权系数进行表达及计算，再通过公式（6）对输入层与隐层之间的权系数进行表达及计算。

式中：Vj，n为输出层与隐层之间的权系数；On为输出层第n个节点输出量；Wi，j为自输入层至隐层的权重系数；i、k为函数计算系数；η为数值增益系数，取值为0～1；δ为惯性系数，取值为0～1。

可根据实际需要，利用数值增益系数η和惯性系数δ调整学习收敛速度。最后结合计算分析结果，构建电气自动化设备的神经网络模型，判断设备是否存在故障[2]。

2 神经网络在电气自动化中的应用优势

2.1 便于调节参数

传统设备参数调节均是通过技术人员的认识及经验来完成的。而应用神经网络技术则可实现对数据的自动学习及特征提取，无须人工参与，可较好降低因人为因素引起的参数调整错误，进而根据实际需要高效、精确地调节相关参数。

2.2 误差小

应用神经网络算法对电气自动化设备故障进行诊断，可不受其他因素影响且设置的参数会始终保持不变，不易发生实际数值与理论数值相差过大的情况，因此诊断误差小。

3 实例分析

为研究神经网络的故障诊断效果，该文以S7-315/10 型变压器为例进行分析。该变压器为三相铜芯10kV 变压器，容量为315kVA。为判断该变压器故障情况、并解决传统故障判别方法精度不高以及对技术人员经验依赖大等问题，首先采用色谱分析法对变压器油气进行分析，以判断变压器实际故障情况，其次重点采用神经网络技术对气体种类、浓度与故障之间的关系进行研究及确定。

3.1 色谱分析

油气色谱分析法的变压器故障诊断

变压器油在变压器中起到绝缘、散热和消弧作用，其故障特征气体种类一般由H2、CH4、C2H6、C2H4、C2H2组成。该文实例分析的大型变压器油中所含气体极限情况见表1。

表1 该变压器油中所含气体极限参数表

故障检测工作原理：当变压器出现设备故障时，表1 中变压器油中的气体会发生不同浓度的变化。这些气体有些是自然存在于油中的，有些是变压器发生故障时机械刺激或放电产生的。利用油气色谱分析法对比变压器中产生的气体含量，就可以实现变压器运行故障的自动检测。其中油气色谱分析法的三类比值法使用最常见，见表2。

表2 油气色谱分析三比值法参数表

造成变压器故障的常见因素有超压及超流、绕组短路、冷却不足、绝缘损坏以及温度过高等，其变压器油的过热、挥发和氧化是工作过程的基本反应。在变压器的实际工作过程中，通常使用的故障检测方法有以下2 种：1）通过专业仪器检测变压器的运行电压、电流、温度、压力和油量等数据，分析变压器的具体故障原因。2）通过使用气相色谱仪手段，对变压器油中的气体进行成分检测及比例分析。

该变压器通过气相色谱仪对变压器的气体进行实际检测和数据分析，并利用模糊神经网络作为智能技术支持，判断出变压器油中气体比例与变压器故障两者之间的关系，利用计算机设定严谨的变压器故障编码，然后从输入端进入神经网络系统中进行机器学习，以此形成更智能的自动化变压器故障检测系统。

3.2 基于神经网络的故障智能诊断过程

根据气相色谱分析的相关参数构建故障诊断模型，并利用神经网络对数据进行训练，以此来达到高效、精准诊断变压器故障的目的。

3.2.1 构建变压器故障智能诊断模型

构建变压器故障检测模型是实现智能诊断设备故障的先决条件，通过电气工程中的专业设备模式识别电流的频率、最大值、最小值和流向等数据变化情况，并标识电气工程中设备运行故障信号的特征表现。然后根据这些特征表现构建智能的电气自动化故障检测模型，如图2所示。另外，一般电气工程中设备规模大且结构复杂，会伴有多种不同的特征表现，因此电气自动化故障检测必须有统一化的处理方式，并对不同的特征表现均有对应的监测模块[3]。

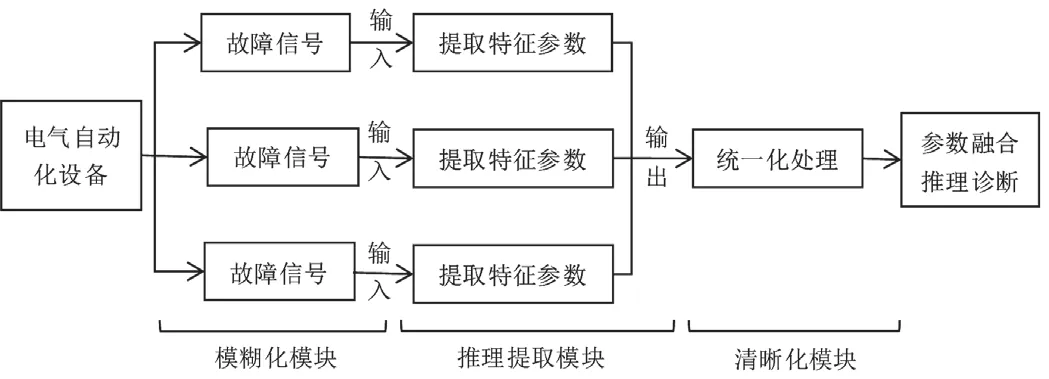
图2 变压器故障检测模型流程图

3.2.2 神经网络识别离散层故障信号

创建电气自动化故障检测模型后，要利用神经网络算法识别电气工程设备运行的离散层故障信息。由于电气工程中设备运行故障信号具有多样性，单一的故障信号不能诊断出设备运行的具体故障原因，因此需要技术人员将电气工程中的设备运行故障信号进行统一化处理，从多样性的故障信号转化为一致性的离散层故障信号。然后将转化后的离散层故障信号进行学习训练，并分析优化离散层故障信号有效值，获取故障信号之间的特征表现关系[4]，如公式（7）所示。

式中：υ为离散层故障信号有效值；xi为电气工程中设备运行故障的线路流经特征（i为实数）；N为电气工程中设备运行故障信号数量（N为实数极值）。

从公式（7）中可得出离散型设备运行故障信号有效值，然后根据电气工程中设备运行故障的流经强度算法，获取故障信号之间的特征表现关系[5]，如公式（8）所示。

式中：p为电气工程中设备运行故障电流极值；Nj是电气设备运行强度故障点的极值特征；xi为电气工程中设备运行故障的线路流经特征（i为实数）。

公式（8）中对xi进行了绝对值处理，故而可以避免设备运行故障时电流的流经方向问题。

3.2.3 变压器行故障检测的定位

根据上述神经网络识别的离散层故障信号以及变压器运行故障检测的定位技术，对变压器运行故障进行智能自动化诊断、预测和分析，主要包括以下3 点：1）要利用获得的变压器运行故障模式，识别分析出每个故障信号的目标值。2）使用神经网络技术优先选择隐藏层的神经元数目和激活函数，作为整个故障检测系统的控制中心。3）采用计算机神经网络算法计算变压器运行的故障幅值，最后分析电气设备运行的自我诊断数据，如公式（9）所示。

式中：s为电气设备的故障幅值；H为初始布拉格波长漂移量；i为光线有效弹光灵敏度；p为光纤有效弹光系数；h为初始布拉格波长；ah为波长应变量；bh为波长频率；ω为波长谐振矢量；υ为离散型故障信号的有效值。

通过公式（9）不仅可获得变压器运行故障信息的统一化控制结果，还可去掉变压器运行故障的不显著信号参数，并增强故障信号参数的稳定性。这样既可保证变压器自我诊断的一致性，也可采用神经网络算法完成对变压器运行故障的自动化检测和分析[6]。

3.3 故障诊断分析

3.3.1 输入模糊规则

因为利用气相色谱分析法对变压器油气分析获得的含量数据差异较大，无法直接输入神经网络，即使进行过优化处理，也还是存在较大差异。因此在数据输入神经网络训练之前采用隶属函数对数据进行优化，以缩小数据差异，并控制数据限值在0～1，使三比值样本转化为适合神经网络的数据形式。这样既能提高数据的可训练性，也能增强神经网络的容错能力，保证诊断结果的准确性。该文研究中应用的隶属函数如公式（10）～公式（12）所示。

式中：X1、X2、X3为变压器油气含量分析数据优化函数值；U1、U2、U3为变压器油气含量实际分析值。

3.3.2 输出转换规则

如果第n个输出的第j个值比其他数值大得比较多，则将该值视作相应故障类型的输出解。如果输出的值中存在2 个最大值或者几个最大值，并且最大值相差较小，而其他输出值偏小，则说明这几个故障发生概率比较大。实际诊断中，将输出值大于0.55 的统一记作1，表示已发生该故障，其他小于0.55的值记作0，表示未发生此故障。

3.3.3 样本训练

选取110 组实测数据中的15 组典型样本，利用神经网络对选取的样本进行模糊处理及训练，将学习率Ir设定为0.3，隐层节点数S1为12，输出节点设有8 个，误差精度取0.1。样本经神经网络模糊处理及训练后形成相应的“权”矩阵，然后统计并记录变压器的故障数据。

3.3.4 诊断结果

通过神经网络完成样本训练后，先自检，再跟实际数据做对比分析，最后诊断出变压器的具体故障情况。具体结果见表3。

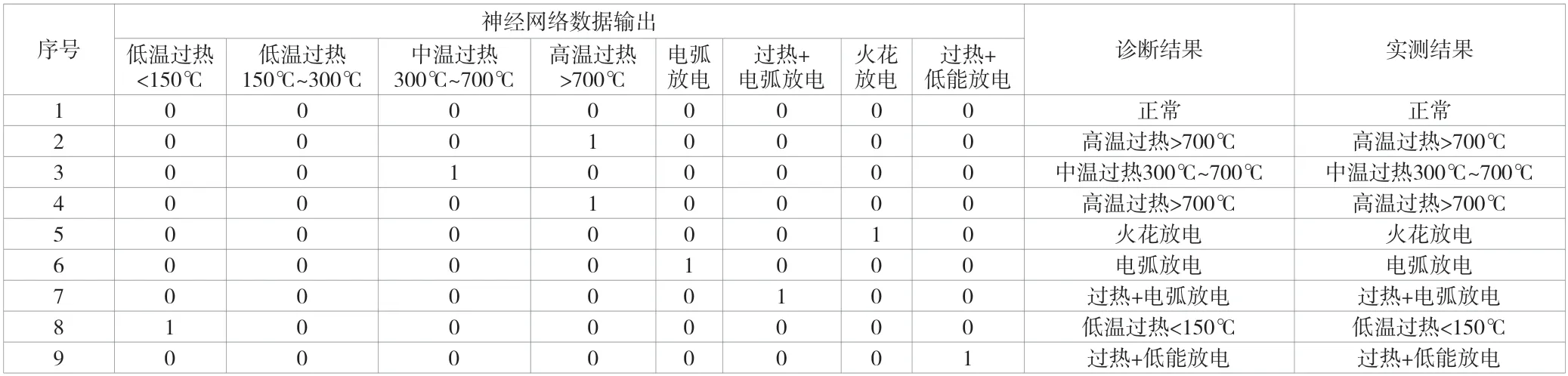
表3 基于神经网络的变压器诊断结果

从表3 可以看出，利用神经网络对变压器故障进行诊断，最终的结果和实际开箱检测结果是一样的，说明该文利用神经网络对变压器故障进行诊断达到了预期效果。

4 总结

综上所述，该文通过实例证明了神经网络技术在电气自动化设备故障诊断中具有良好的效果，不仅诊断结果准确，还不易受其他因素影响，诊断效率也比较高，可有效解决依赖技术人员经验及其他系统信息等问题，并且可通过准确描述故障情况来确定故障位置，可为电气自动化设备稳定性运行提供保障。