强场原子电离响应时间的研究进展*
2023-10-30车佳殷陈超李卫艳李维陈彦军
车佳殷 陈超 李卫艳 李维 陈彦军
1) (河北地质大学数理学院,河北省光电信息与地球探测技术重点实验室,石家庄 050031)
2) (陕西师范大学物理学与信息技术学院,西安 710119)
3) (邢台学院物理与电子工程学院,邢台 054001)
4) (中国空间技术研究院,北京空间机电研究所,北京 100094)
1 引言
阿秒光学是近二十年来伴随着超强超短激光脉冲技术的快速发展而兴起的一门学科,其研究在阿秒尺度测量和操控物质内部电子运动的手段和理论,为人类认识微观世界提供了崭新工具.超强超短激光脉冲与物质相互作用[1,2]会产生丰富的超快物理现象,如阈上电离[3−6]、高次谐波辐射[7−10]和非次序双电离[11−13]等.人们进一步把这些现象用于超快探测[14,15],发展了可用于研究隧穿时间的阿秒钟技术[16]、可用于监测散射电子运动轨道的高次谐波光谱技术[17]以及可用于探测电子Wigner时间延迟的阿秒条纹相机技术[18]、RABBITT 方法[19,20]等.虽然阿秒测量取得了一系列令人鼓舞的发现和成果,但仍处于发展的初始阶段[21],存在一系列亟需解决的问题.目前阿秒测量遇到的关键问题主要分为以下三个方面.
1)理论上,量子力学中没有时间算符,对时间的“测量”是量子力学的基本问题[22−24].这就使得即使对于简单的系统,对新的阿秒测量结果的解释也很复杂,引出了许多概念和理论上的问题,诸如哪些时间信息可以获取,哪些过程可以操控,短期动力学如何决定更复杂系统的电子特性等.其中一个基本的概念问题是在光电效应过程中,电子吸收一个光子是否需要时间,或者从量子角度说,电子波函数是否对光吸收事件存在响应时间,从而导致电离时间延迟.对于单光子电离(一类弱场诱导的光电效应),阿秒条纹实验测量到了Ne 原子价电子和内层电子的相对电离时间延迟,并指出这一延迟对应Wigner 时间延迟[23].但相关实验也引出了许多问题: 首先,实验测量到的条纹移动无严格理论将其与Wigner 时间延迟对应[24];其次,Wigner 时间延迟对应与电子自由运动情况相比下电子波包的额外量子相位偏移,而不是吸收光子的实际时间[25];最后,实验得到的只是相对延迟,而不是绝对延迟.对于强场隧穿电离(一种强场诱导的光电效应),阿秒钟实验测量到了He 原子隧穿电离时间延迟的上限为几十个阿秒[25],但也引出了许多问题: 首先,对另外原子的一些实验给出了不同的结果,即不存在隧穿时间延迟[26,27];其次,没有严格的理论来建立实验观测量(即光电子动量分布(photoelectron momentum distribution,PMD)偏移角)与隧穿时间延迟的映射关系[27];最后,没有统一的理论可以定量描述针对不同原子分子和不同激光参数测量到的偏转角[25−30].
2)实验上,目前的超快测量技术无法直接实现对过程的阿秒分辨,而需要通过理论模型从实验观测量反演时间信息.超快探测实验观测光与物质相互作用结束后系统的频域信息,比如光电子谱、光辐射谱(谐波谱)或光吸收谱,然后通过建立的理论模型从这些谱中反演电子运动的阿秒时间信息,进而实现阿秒分辨测量[16,17].因此,理论模型在目前的阿秒探测方案中具有关键作用,理论模型的精确性将决定反演信息的精确性[31],进而直接影响对实验结果的解释或者对所测量过程的描述.上面讨论的阿秒条纹实验和阿秒钟实验目前存在的问题,很大程度上也源于没有精确统一的理论模型描述相关过程,进而也无法建立观测量和时间之间的精确唯一的映射.
3)研究对象上,目前的阿秒探测主要集中在原子,对于分布更广泛、结构更丰富的分子的探测亟需深入.分子特别是极性分子[32,33],由于具有更多的自由度,其在强激光场中会呈现许多新的效应,例如两中心干涉[34]、准直和取向[35,36]、固有偶极子[37]和核的振动[38]等.对于复杂的分子,例如陀螺分子,还具有不同的构型.在关于分子的阿秒探测中,需要充分考虑上述分子特有的效应,发展适合的理论模型以描述、寻找适合的特征量以表征、构建适合的探测方案以测量上述效应.上述效应本身除了可作为阿秒探测的“对象”,还能作为有效手段去获取系统结构或动力学信息.
理论模型在阿秒测量实验中起到了关键的作用.目前人们常用的模型包括半经典模型[3,9]和量子[5,6]的强场近似模型.这些模型通过电子轨道概念(包括长轨道和短轨道)描述电子的运动,即针对每一个频域观测量,比如光电子动量或谐波能量,在时域上都有确定的电离时间(以及返回时间)与之对应,因此在拟观测过程的频域和时域之间建立起了联系[31].根据这些电子轨道,即可通过频域观测量反演系统时间信息.通常的强场理论模型未考虑库仑效应,而相关研究已表明[39,40]该效应对系统的光电子能谱[41]、动量谱[42]和角分布[16]等都具有重要影响.近些年来,已经发展了包含库仑效应的针对强场电离的半经典或量子理论模型[39,42].这些模型对于理解电子在激光场和库仑场共同作用下的超快动力学起到了重要作用.然而由于强场电离过程涉及库仑-电子-外场三体之间复杂的相互作用,对此过程中库仑效应的解析描述一直是理论的难点,不同的近似处理会给出观测量和时间之间不同的映射.
关于上述问题,本文提出了针对原子强场电离的响应时间理论[43],响应时间对应于可测量的库仑-电子-外场三体强相互作用时间,可在量子和经典边界处确定.从系统对称性出发,引入位力定理和冲量定理便可得到由系统基本参数决定的响应时间公式,进而得到时间和观测量之间的简单映射.该理论能定量重现近年来系列阿秒钟实验曲线,为相关实验现象提供了统一的理论框架.
2 理论方法
接下来详细介绍强场响应时间理论模型,该模型基于强场近似(SFA)[5],但进一步考虑了库仑效应[39,42,44].响应时间理论模型考虑母核附近电子感受到的主要库仑效应,假设在隧穿出口电子处于一个过渡态(高里德伯态),该状态同时具有束缚态和连续态的性质.隧穿电子从该过渡态转变为电离态需要一段有限的时间(响应时间).这个时间又可以表征为库仑诱导的电离时间延迟,结合位力定理和冲量定理,给出了该延迟时间的解析表达,并进一步建立了实验观测量与电离时间之间清晰的映射关系.该映射关系为人们定量研究强场光电效应响应时间提供了一个简单的工具.
2.1 不包含库仑的动量-时间映射关系
结合强场近似(SFA)鞍点理论[5,6],对强场电离事件起到主要贡献的是一系列特定的电子轨道,这些轨道对应的光电子动量p满足以下鞍点方程:
其中A(t) 是电场E(t) 的矢势.时间ts=t0+itx是复数,实部t0又可以理解为隧穿出射时间.当不考虑库仑效应的时候,隧穿出射时间t0就对应于电子的电离时间.取(1)式中电离能Ip=0,可以得到Simple-Man (SM)模型的动量时间映射关系:
对于真实的原子情况Ip≠0,可以给出SFA关于动量时间的映射关系:
其中,v(t0)=p+A(t0) 是隧穿出点位置r0≡r(t0)=处电子的初速度[45].该速度反映了电子隧穿的基本量子效应.对应于电子轨道 (p,t0) 的复振幅表示为c(p,t0)≡c(p,ts)~e-b,其中b是准经典作用量Ip}dt′的虚部[5].
2.2 包含库仑的动量-时间映射关系
阿秒钟实验巧妙地运用椭圆偏振激光场中PMD 的偏转角作为特征量来提取电子隧穿时间信息[16,25,26,29,30].椭圆偏振激光场具有以下形式:
其中,
EL对应于脉冲峰值强度I的最大激光振幅.ε是椭偏率,ω是激光频率,f(t) 是包络函数.可以通过对比理论和实验得到的椭偏场中的PMD 偏转角及相关动量来检验理论模型的准确性.
强椭圆偏振激光场作用下电子的隧穿位置可粗略估计为r0≈Ip/E0.对于实验中通常用到的激光参数(如He 原子在强度I=5×1014W·cm-2、椭偏率ε=0.87 的激光场中),电子的隧穿出点距离母核中心约10 a.u..在这个位置,哈密顿量H0=p2/2+V(r)的一系列高能束缚态占有较大的概率.因此假设对于一个真实的原子,在隧穿出点r(t0)附近,具有动量p的隧穿电子波包是由一系列H0的高能束缚态构成的.换言之,在t0时刻隧穿电子处于一个准束缚态,其中|n〉是H0的本征态.这个准束缚态近似满足位力定理,即.实际上,
其中,非对角项对于平均势能的贡献为
实际计算中,不同非对角项之间相互抵消,而且一个非对角项的振幅绝对值一般情况下小于对应的对角项.所以,〈V(r)/2〉n≠m的振幅通常小于〈V(r)/2〉,后者既包含了对角项又包含了非对角项的贡献.
根据前面的介绍,准束缚态还具有连续态的性质.接下来延续SFA 的观点,认为电子在t0时刻隧穿出垒,可以将其视为一个自由粒子.进一步假设考虑库仑效应的时候,可以将束缚电子波包当作一个具有库仑诱导速度vi的准粒子进行处理.库仑诱导速度vi满足vi=-|vi|r0/r0,其中,且
这里,nf=2,3 是单电子系统的自由度.隧穿出点处库仑诱导速度vi与激光场诱导的初速度v(t0) 方向相反.再根据SM 图像[9],准自由粒子在t0时刻沿着总电场E(t) 的方向发生隧穿之后,具有一个激光诱导的初速度v(t0) 和一个库仑诱导的初速度vi,满足下面的映射关系:
其中,p′是库仑修正的隧穿电子漂移动量,速度vi描述了隧穿过程中电子靠近核感受到的库仑势的影响.另外,研究表明相比于SFA,强场电离过程中的库仑效应表现为一个电离时间延迟[31].考虑该延迟效应,假设从t0时刻到ti=t0+τ时刻关系式-A(ti)≃vi-A(t0) 成立.进一步可以得到:
结合(4)式和(5)式可以知道,与速度vi相关的库仑效应在电离时间ti和隧穿时间t0之间诱导产生了一个延迟τ.在时间ti之后,隧穿电子自由,且初速度满足v(ti)≡v(t0),电子仅在激光场的作用下运动,可以忽略库仑效应的影响.
结合上面的讨论,延迟τ可以被进一步理解为强场光电效应中原子内部电子对光的可观测响应时间.具体来说,由于库仑势的存在,电子在时间t0到达隧穿出点并未立即自由.在激光场的作用下,电子波包需要一段有限的响应时间(对应延迟τ)从一个同时具有束缚态和连续态性质的准束缚态演变为无库仑的电离态.在实际处理中,时间t0之前的隧穿过程通过SFA 鞍点理论进行描述,隧穿不需要时间;电离时间ti之后,可以忽略库仑效应;因此,延迟τ(响应时间)包含了电子、核以及光子三体强相互作用所有的可观测时间.
2.3 包含库仑的角度-时间映射关系
在阿秒钟实验中,PMD 偏转角通常是针对具有最大振幅的最可几轨道(MPR)定义的.MPR对应特定的电子轨道 (p,t0),其中t0是椭偏光主场的峰值时刻|Ex(t0)|=E0.而且对于MPR,沿着主场方向的初速度vx(t0)=0,沿着副场方向的初速度vy(t0) 由于非绝热效应不为零[28].结合(5)式可以得到MPR 动量分布偏转角的表达式:
该式建立了动量分布偏转角θ与电离时间ti=t0+τ之间的映射关系.通过该映射,若已知实验或TDSE 偏转角,就可以进一步得到时间延迟τ.当Keldysh参数远小于1的时候[1],考虑到|vy(t0)/Ay(t0)|≪1,有p′ ≈-A(ti).这里相当于将延迟τ引入到了SM 模型映射关系p=-A(t0)中.进一步得到MPR 光电子动量分布偏转角的绝热版本表达:
2.4 响应时间
接下来给出MPR 响应时间的解析表达式.根据上述推导,-A(ti)≃vi-A(t0),以及|vi|=,结合冲量定理,可以得到
对应于MPR 的响应时间可以表示为
在求解(1)式鞍点方程的过程中忽略Ey(t) 的影响,可以得到隧穿出点位置r(t0) 的近似表达式以及y(t0)≈0.考虑单活性电子近似,对于类氢原子库仑势满足V(r)=-Z/r,Z是有效电荷.可以进一步得到延迟(响应时间)的解析表达式:
对于三维情况,(9)式中电荷量可取为Z=;对于二维情况,电荷量可以选择为模拟中使用的数值.(9)式表明,延迟τ随着激光振幅E0以及激光波长λ的增加(对应于激光频率ω的减小)而减小.而且可以判断二维情况下(nf=2)的延迟要大于三维情况(nf=3).当Keldysh 参数γ ≪1时,进一步得到x(t0)≈(Ip/E0)(1-γ2/4),延迟可进一步表示为.
需要注意的是(8)式仅适用于长程库仑势,对于短范围势(例如Yukawa 势)情况,在隧穿位置处库仑势近似为零,因此(8)式预言此时的响应时间为零,这也与我们相关的TDSE 模拟结果一致.对于具有短程势的1 价负离子体系的电离过程,上述预言需要相关实验的进一步检验.另外,在求解鞍点方程的过程中忽略Ey(t) 的影响,可得到沿着副场方向电子的初速度
将TRCM 理论得到的时间延迟τ以及初速度vy(t0)代入(6)式,可以解析计算光电子动量分布的偏转角.
2.5 TRCM 模型
(8)式是针对强椭圆偏振激光场中的MPR 讨论的.可以将其推广至任意SFA 电子轨道(p,t0)以及不同形式的激光场,表达式为
其中,|E(t0)|是t0时刻的激光场振幅.对于椭圆偏振激光
一旦得到了延迟τ,结合(5)式p′=v(t0)-A(ti=t0+τ),v(t0)=p+A(t0) 就可以得到库仑修正之后的动量.假设库仑修正的电子轨道 (p′,ti) 对应的振幅c(p′,ti) 等于对应的SFA 电子轨道 (p,t0) 的振幅c(p,t0)~e-b.其 中b >0 是准经典作用量的虚部[5],就可以直接得到考虑库仑修正的光电子动量分布,不需要再求解包含电场力和库仑力的牛顿方程.借助响应时间的概念,强场隧穿电离可以被分为3 个基本过程,即隧穿(tunneling)、响应(response)和经典运动(classic Motion),如图1(a)中(I)—(III)所示,这3 个过程可以分别通过鞍点理论、半经典以及经典理论进行描述,并由此建立了TRCM 理论模型.图1(a)中,电子在激光主场峰值时刻t0隧穿出垒(满足px ≡px(t0)=0),受到库仑作用电子并未立即自由,从时间t0到电离时间ti有一段延迟τ=ti-t0.这个延迟反映了强场隧穿电离过程中电子对光的响应时间,可通过(8)式和(9)式进行量化.凭借TRCM 模型,可以直接通过图1(c)中不包含库仑效应的SFA 动量分布,得到图1(d)中考虑库仑修正的动量分布,而且图1(d)的偏转角结果与图1(b)中数值实验(TDSE)的结果定量一致.
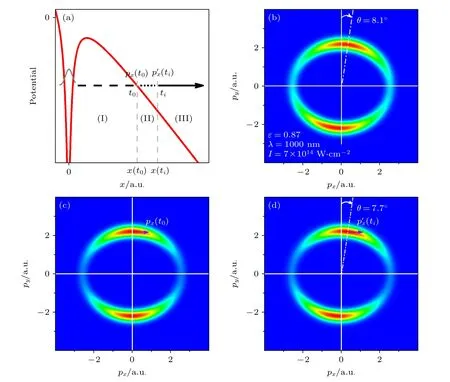
图1 强场隧穿电离过程示意图及光电子动量分布结果比较[43] (a) 强场隧穿电离示意图,电子在 t0 时刻隧穿出垒,对应隧穿过程(I);响应过程(II)发生在 t0 — ti 之间;ti 时刻之后,电子电离并做经典运动,对应过程(III).(b) TDSE 光电子动量分布,激光参数以及偏转角大小如图所示;(c) SFA 光电子动量分布;(d) TRCM 光电子动量分布,偏转角θ=7.7°.图(c),(d)的激光参数与图(b) TDSE 一致,且图(d)中TRCM 参数选择nf=2Fig.1.Sketch of strong field tunneling ionization process and comparison of PMD results[43].(a) Sketch of strong field tunneling ionization,electron exits the barrier at the peak time t0 of the laser field,in (I) process,the response process (II) occurs between the exit time t0 and the ionization time ti ;after time ti,the electron makes a classical motion,corresponding to the process (III).(b) PMD result of TDSE,laser parameters and offset angle are as shown;(c) PMD result of SFA;(d) PMD result of TRCM and the offset angle is also shown.Panels (c) and (d) use the same laser parameters as panel (b) TDSE,and the parameter nf=2 is selected in TRCM.
2.6 适用性分析
首先,TRCM 模型假设在电离时间ti之后,库仑效应对于隧穿电子动力学的影响可以忽略.因此,该模型没有考虑电子随后可能发生的库仑再散射(结合)效应.尤其是当使用椭偏率较小的椭偏光作用于原子分子的时候,直接电离的电子可能会与再散射电子发生干涉效应从而影响到PMD可观测量.近期相关研究借助TRCM 理论模型,系统地对比分析了激光椭偏率对于阿秒钟PMD偏转角等可观测量的影响,结果指出在椭偏率0.45—1.0 范围内,TRCM 模型能够对实验结果给出较好的定量预言[46].
另外有一点需要说明的是,在理论部分提到库仑诱导速度vi和平均动能的关系的时候引入了参量nf.对引入该参数的物理依据做如下陈述: 根据量子力学基本规律,束缚波函数的对称性反映了系统库仑对称性的基本要求.响应时间理论假设电子在隧穿出点处于一个准束缚态,其波函数具有类似S 态的对称分布(动能沿着电子运动的自由度平均分配),且系统的平均动能与平均势能近似满足位力定理,即nf表示系统的自由度.隧穿出点原子的电子波函数的类S 态对称分布由其库仑对称性决定.电子要发生隧穿电离,从束缚态变为连续态,就要打破这种内在库仑对称性的要求,最直接的方式就是从外场中获得-|vi|的冲量沿着隧穿方向(电子运动的一个自由度方向)破坏库仑对称性.简单来讲,库仑对称性决定隧穿出点(准)束缚波函数对称性,束缚波函数对称性决定动能依据nf平均分配.
3 响应时间理论模型的应用
响应时间理论模型(TRCM)可应用于不同靶材及不同形式的激光场,为定量解释和预言阿秒超快物理现象提供了一个简单的工具.接下来详细介绍该模型的相关具体应用.
首先,TRCM 理论模型不仅可以定量地重现系列阿秒钟实验曲线,还能对这些实验给出一致的物理解释[43].例如在图2 和图3 所展示的实验研究中,对于H 原子的实验偏移角的解释[26,27]是不存在隧穿时间延迟,而关于He 和Ar 的实验偏转角的解释[28,29]则是存在有限的隧穿时间延迟.这些关于相似实验现象的不同解释源于对实验结果的分析中采用了不同的理论模型.这些理论模型均通过实验的观测量来反演时间,且被应用于解释特定实验结果.与上述模型方案处理不同,响应时间理论模型首先根据激光和原子参数计算响应时间,然后根据响应时间得到实验观测量.结合图2 和图3 可以看到,针对不同气体靶或激光参数TRCM理论预言的光电子动量分布偏转角以及电离时间延迟,与实验结果均符合得很好.TRCM 理论模型统一解释了这些不同实验中观测到的偏转角,即这些偏转角均起源于强场电离过程中电子对光的响应,其大小反映了响应过程的时间尺度.
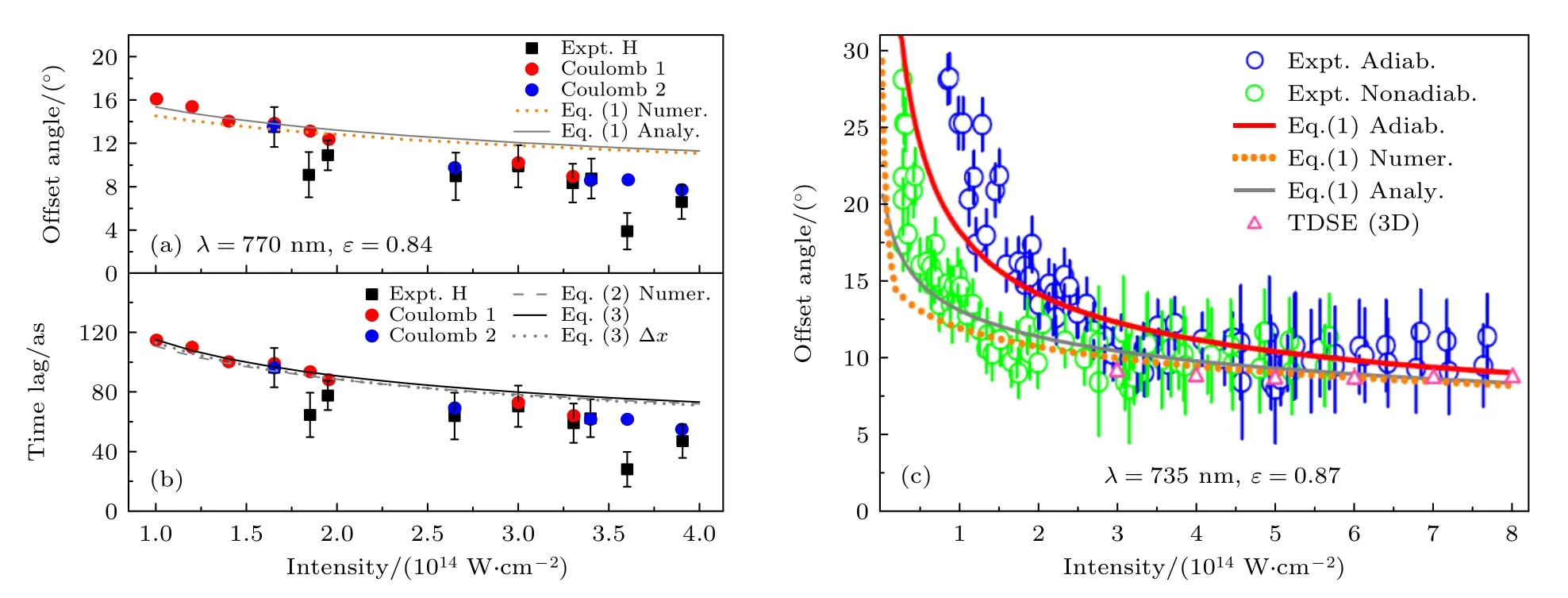
图2 响应时间理论应用于H (a),(b)和He (c) [43].图中的实、虚线是响应时间理论预言的结果,点和圈是实验或TDSE 的结果.需要强调,图中的Eq.(1)— Eq.(3)依次对应于本文(6)式、(8)式、(9)式.(a) 响应时间理论计算所得偏转角与文献[26]实验(Exp.H)和TDSE 结果(Coulomb 1 和Coulomb 2)的比较.(b) 响应时间理论计算所得延迟时间与文献[26]实验(Exp.H)和TDSE 结果(Coulomb 1 和Coulomb 2)的比较.(c) 响应时间理论计算得到的偏转角(包含绝热版本)与文献[28]中的实验(Exp.)以及三维TDSE 结果的比较Fig.2.Application of response time theory to H (a),(b) and He (c) [43].Real and dashed lines are the predicted results of response time theory,while the points and circles are the results of experiments or TDSE.It should be emphasized that Eq.(1)−Eq.(3) in these figures,corresponding to the Eq.(6),Eq.(8),Eq.(9) introduced in the theoretical section: (a) Comparison of the offset angles calculated by response time theory with the experimental (Exp.H) and TDSE (Coulomb 1 and Coulomb 2) results in Ref.[26];(b) comparison of lag time calculated by response time theory with experimental (Exp.H) and TDSE (Coulomb 1 and Coulomb 2)results in Ref.[26];(c) comparison of the offset angles calculated by response time theory with the experiment (Exp.) in Ref.[28]and our three-dimensional TDSE results.

图3 响应时间理论应用于其他气体靶[43].图中的灰实线和橙色点线是TRCM 理论给出的偏转角结果;蓝色点为实验以及TDSE 的结果;Eq.(1)对应于理论部分介绍的(6)式 (a) 与实验He 结果(Exp.He) [29]比较;(b) 与实验Ar 结果(Exp.Ar) [29]比较;(c) 与实验H2 结果(Exp.H2) [30]比较;(d) 与H 的TDSE 结果(TDSE H) [27]比较.在所有情况中,TRCM 理论均很好地预言了实验的偏转角Fig.3.Application of response time theory to other gas targets[43].Gray solid lines and orange dotted lines are the offset angle results of TRCM theory,while the blue dots represent the results of experimental and TDSE;Eq.(1) in these figures,corresponding to the Eq.(6) introduced in the theoretical section: (a) Comparison between theoretical angles with the He experimental results (Exp.He) [29];(b) comparison between theoretical angles with the Ar experimental results (Exp.Ar) [29];(c) comparison between theoretical angles with the H2 experimental results (Exp.H2) [30];(d) comparison between theoretical angles with the TDSE results (TDSE H) of H [27].In all cases,the TRCM theory predicts the offset angle of the experiment well.
其次,TRCM 理论模型可以用来得到阿秒钟实验观测量的标度律公式[46].在实验研究过程中,精确地标定激光强度是困难的,系统的研究激光椭偏率对阿秒钟实验观测量的影响,将会为实验结果的场强依赖规律提供有益的补充[28].通过比较激光椭偏率对动量分布偏转角及相关动量的影响,结果显示,随着椭偏率的增大动量分布偏转角减小,而沿着偏振主轴方向的动量变化缓慢,沿着偏振副轴方向的动量增加明显.这些现象均与实验结果保持一致,如图4 所示.借助TRCM 理论模型,得到了阿秒钟实验偏转角及相关动量对椭偏率依赖的标度律公式,而且进一步给出了编码在该偏转角中的库仑诱导电离时间延迟(响应时间)对激光椭偏率的依赖关系.标度律的提出有望为人们更好地理解阿秒钟在不同条件下的适用性及可行性提供系统的理论参考.
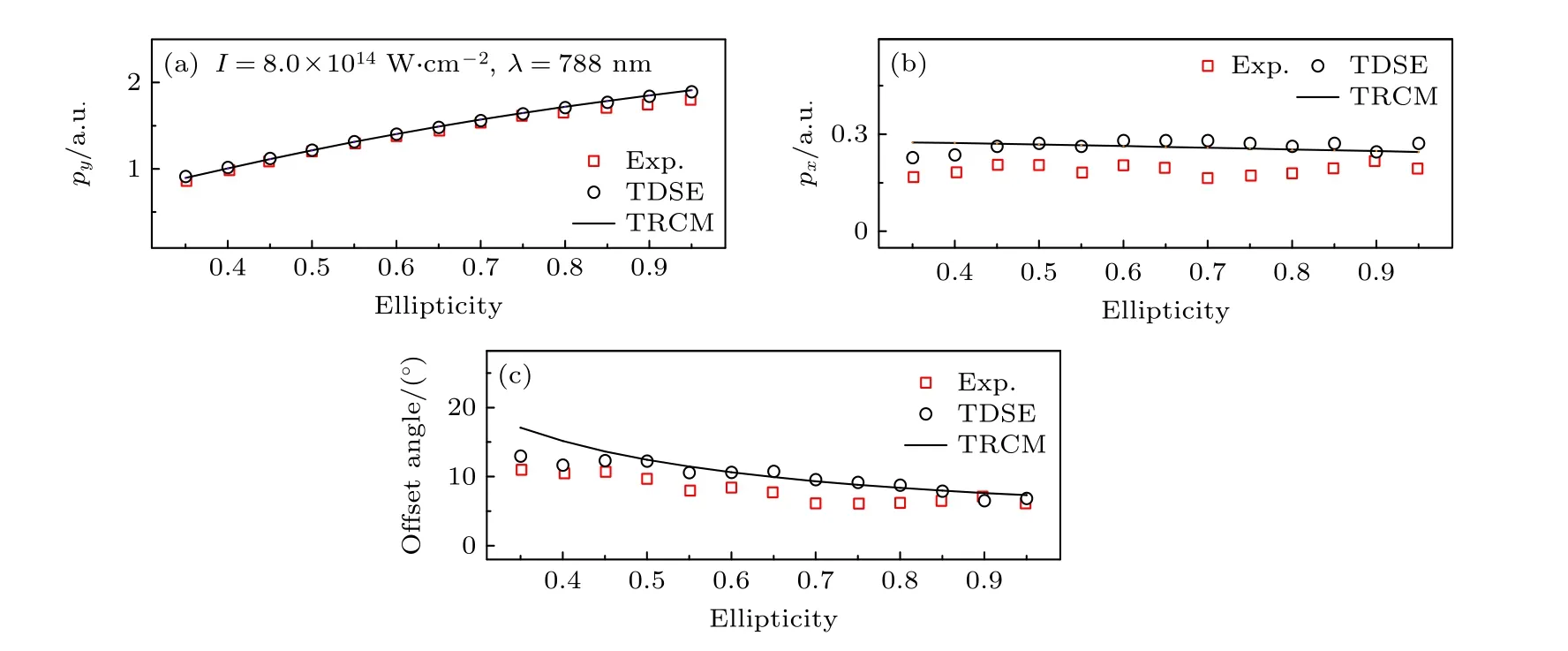
图4 应用响应时间理论得到阿秒钟椭偏依赖的标度律关系[46].实线是TRCM 理论模型的结果,空心符号分别是TDSE 和实验[47]的结果 (a),(b) 动量分布最亮点(最可几轨道)对应沿着激光偏振主轴方向 px 和副轴方向 py 的动量比较;(c) 动量分布偏转角结果的比较Fig.4.Applying response time theory to obtain the scaling law for the ellipticity dependence of the observable in attoclocks[46].The solid line is the result of the TRCM,while the hollow symbol are the results of TDSE and experimental[47],respectively:(a),(b) Comparison of the momentum along the laser polarization main axis px and the minor axis py corresponding to the brightest point (most probable route) of the PMD;(c) comparison of the results of PMD offset angles.
TRCM 理论模型还可以应用于不同形式的激光场,例如正交双色激光场[48],得到的原子光电子动量分布如图5 所示.可以看到,动量分布呈现出了明显的上下不对称蝴蝶结构.这种不对称结构在SFA 的结果中消失,在TRCM 和考虑库仑修正的强场近似(MSFA)结果中重现.进一步研究比较发现,TDSE 光电子动量分布呈现出了两个特征结构,一个矩形结构可以形象地理解为“蝴蝶的身体”,还有一个肩状结构.正交双色激光场中这两个典型结构的位置依赖于激光参数.借助TRCM模型分析可以知道这两个结构起源于原子内部电子对于正交双光诱导光辐射过程的阿秒响应.我们还给出了可以定量计算这两个结构位置的数学表达式(即矩形边界、肩结构E0和E1分别是正交双色激光场主场和副场的振幅,τ为响应时间),凭借该表达式可以建立基于正交双光精准操控电子出射的高分辨双光阿秒计时仪.

图5 响应时间理论应用于正交双色激光场[48] (a) TDSE 动量分布结果;(b) 响应时间理论(TRCM)结果;(c) 库仑修正的强场近似(MSFA)结果;(d) 强场近似(SFA)结果.图中水平白线展示TRCM 预言肩结构对应位置数值,垂直双白线中间部分是矩形结构,水平红色箭头指示矩形结构的宽度.可以看到TRCM 肩结构及矩形结构的位置与TDSE 的结果定量上一致Fig.5.Application of response time theory to orthogonal two-color (OTC) laser field[48]: (a) PMD of TDSE;(b) PMD of TRCM;(c) PMD of Coulomb-modified strong field approximation (MSFA);(d) PMD of SFA.The horizontal white line in each figure displays the shoulder position values predicted by TRCM,the middle part of the vertical double white lines is a rectangular structure,and the horizontal red arrow indicates the width of the rectangular structure.It can be seen that the positions of the TRCM shoulder and rectangular structure are quantitatively consistent with the results of TDSE.
TRCM 理论模型还可以被进一步推广到分子体系[49].通过数值模拟发现对称分子相较于同样电离能的原子,光电子动量分布偏转角会大2°—3°.随着分子的核间距增大,二者之间的角度差进一步增大.通过在原子TRCM 理论模型基础之上进一步考虑分子库仑势的双中心特性,发展了适用于分子体系的响应时间理论. 分子TRCM 理论不仅定量的再现了TDSE 的结果, 而且揭示了相同电离能条件下, 分子内部电子对于强场诱导电离事件的响应显著区别于原子. 详细来说, 相同激光作用下, 分子双中心形成的势垒相较于原子更低更窄, 分子相较于原子的隧穿出点位置更靠近于系统质心; 相同电离能下, 分子的库仑有效电荷量更大.这些因素一致贡献于分子内部电子隧穿之后相较于原子会感受到更强的库仑效应, 从而导致分子体系具有更大的电离时间延迟, 对应于更大的动量分布偏转角. 结果表明, 分子在强场隧穿电离过程中的响应时间比原子长10—20 as 以上, 如图6 所示.

图6 响应时间理论应用于分子体系[49] (a)相同激光参数下对称分子离子 和同样电离能的模型原子势函数曲线比较, 插图是放大隧穿出点位置处两者的区别; (b)—(j) 不同激光参数条件下TDSE 及TRCM 理论给出的 和原子动量分布偏转角、电离时间延迟的比较Fig. 6. Application of response time theory to molecular system[49]: (a) Comparison of potential function curves of symmetric molecular ion and model atom with the same ionization energy under the same laser parameters, the inset magnifies the difference at the tunneling exit; (b)−(j) comparison of and model atom PMD offset angles and ionization time lags given by TDSE and TRCM under different laser parameters.
相较于原子和对称分子,极性分子由于具有固有偶极,其在强激光场中的动力学包含隧穿、激发和Stark 效应等基本量子过程,且电子相对于不同核的运动形成了鲜明的参照.这为研究响应时间提供了一个理想的平台,既方便于研究这些基本过程与响应时间之间的内在联系,又可以检验强场理论的适用性.最近关于极性分子强场电离的研究结果展示,线偏振单色激光场中极性分子HeH+光电子动量分布呈现了显著的左右不对称性[50].进一步分析表明该不对称性源于极性分子库仑和固有偶极之间复杂的相互作用,其中库仑诱导的电离时间延迟(响应时间)具有基本作用.利用这一与响应时间紧密相关的光电子动量分布的不对称性,可以在亚周期内探测极性分子的电离动力学.例如,利用正交双色激光场中极性分子动量分布各象限权重的不对称性,可以探测极性分子在亚周期内的激发态动力学[51];利用椭圆偏振激光场中极性分子动量分布上下偏移角的不对称性,可以分辨极性分子在亚周期内的固有偶极效应[52],如图7 所示.

图7 响应时间理论应用于极性分子体系[52].(a)—(c)不同方案得到的极性分子HeH+光电子动量分布结果比较 (a) TDSE;(b) MSFA-PD;(c) MSFA.(d) TRCM 理论模型偏转角公式的绝热版本给出的角度-时间对应曲线,脉冲前后半个周期极性分子的偏转角相差2°—3°.(e)—(j) 不同激光参数下脉冲前后半个周期极性分子电离时间延迟(响应时间)及差值的比较.前后半个周期响应时间展示了10—20 as 的差异θ=arctan[Ax(t)/Ay(t)]Fig.7.Application of response time theory to polar molecular system [52].(a)−(c) Comparison of PMD results of polar molecules HeH+obtained from different methods: (a) TDSE;(b) MSFA-PD;(c) MSFA.(d) Corresponding curve of offset angle and time given by the adiabatic version of the TRCM model,the offset angle of polar molecules in the first and second half laser cycle differs by 2°−3°.(e)−(j) Comparison of the ionization time lag (response time) and lag difference of polar molecules in the first and second half laser cycle under different laser parameters.The time lag of polar molecules in the first and second half laser cycle differs by 10−20 as.θ=arctan[Ax(t)/Ay(t)]
4 讨论与总结
对近年来激光诱导原子分子光电效应中相关阿秒测量研究进行简单的讨论和总结.在一般的阿秒钟实验中[25],光电子动量分布偏转角θ被认为是由两部分构成: 第1 部分θdelay认为是与隧穿时间延迟τ相关的偏转,满足θdelay≈ωτ;第2 部分θref认为是隧穿电子远离母核过程中库仑效应诱导的偏转.实验上最先测量得到θ,然后通过半经典模拟得到θref(半经典模拟中认为不包含隧穿时间延迟,因此模拟得到的偏转角就是θref),最后从θ中减去θref就得到θdelay.如前所述,根据上述方案针对不同原子的实验得到了不同的结果,潜在的原因之一可能是在半经典模拟中,总要选择模型势来近似模拟靶原子在激光场中动力学,而选择不同的模型势可能导致计算出的θref存在一些差异.
通过TDSE 和包含库仑效应的强场近似研究了正交极化双色场中原子的电离[31].在研究中同时计算瞬时电离产量和光电子动量分布.瞬时电离产量通过从整个含时波函数中实时减去能量较低的束缚态成分而得到,因为能量较低的束缚态波函数主要分布在核附近,因此得到的瞬时电离产量可以近似认为反映了隧穿出点附近的连续态实时布局数,即电子在隧穿出点附近的实时电离行为,这时电离的电子还未远离核.计算得到的TDSE 瞬时电离速率(瞬时电离产量关于时间的导数)最大值对应时刻ti相较于外场峰值时刻t0存在百阿秒的偏移τ,即ti=t0+τ.在将瞬时电离产量和TDSE动量分布结果进行比较的过程中,进一步发现光电子动量p′和电离时间ti近似满足关系式p′ ≈-A(ti)((5)式的绝热版本,见关于(7)式的讨论).该式意味着包含库仑诱导的电离时间延迟τ的实际电离时间ti和包含库仑效应的实际光电子动量p′仍然存在一一对应关系,库仑对光电子动量的影响基本由库仑诱导的电离时间延迟决定.将关系式p′ ≈-A(ti)应用于椭圆偏振激光场[52],这就意味着光电子动量分布的整个偏转角θ均是由库仑诱导电离时间延迟τ导致的(见(7)式).TDSE 模拟中瞬时电离产量和光电子动量分布的紧密对应为强场电离中充分的时间延迟物理图像的建立提供了直接依据.关系式p′ ≈-A(ti) 包含的时间延迟物理图像可理解如下: 隧穿电子在母核附近相较于远离母核会感受到更强的库仑效应.库仑效应对于隧穿电子的主要影响(即电子感受到的关键库仑作用)发生在电子隧穿通过被外场压弯的势垒过程中.可以想象,库仑力将阻碍电子立即脱离母核发生电离,使得隧穿电子的电离时间从无库仑时候的t0延迟到了考虑库仑时候的ti=t0+τ,之后的库仑效应可以忽略.因此电子在隧穿电离过程中感受到的库仑效应等效于延迟电离,即电离时间从无库仑时候的t0变为包含库仑效应时候的ti.使用上述延迟概念,研究发现可以清晰地解释很多复杂的强场物理现象[50−53],因此可认为这个延迟τ反映了一个基本的物理时间,即强场电离中原子内部电子对光的响应时间;从量子力学角度来看,该延迟反映的是电子波包对于强场电离的响应时间.
基于TDSE 的结果,进一步提出了响应时间理论模型(TRCM 模型)来定量描述时间延迟τ[43].TRCM 模型将该延迟描述为可以在量子与经典边界处明确定义并测量的库仑-电子-外场三体强相互作用时间.该模型的主要观点可以简述为: 当电子在外场峰值时刻t0到达隧穿出点r(t0) (一般大约距离母核10 a.u.)并不是立即自由,隧穿电子仍然处于一个准束缚态(一个由无场哈密顿量H0系列高能束缚态构成的波包),该状态近似满足位力定理.该状态可以被进一步当做一个具有库仑势诱导速度vi的准粒子进行处理.速度vi的方向指向母核,与t0时刻电子出射位置矢量方向相反.根据冲量定理,电子需要从外电场中获得|vi|=E0τ的冲量来抵消掉隧穿出点处库仑诱导的速度.当时间大于ti=t0+τ之后,库仑效应的影响可以忽略,电子自由.根据上面的分析,可得到时间延迟τ,即响应时间的解析表达式,即(8)式.
在关于弱场光电离时域性质的阿秒测量中,还经常会用到Wigner 时间延迟的概念[54].Wigner时间延迟被定义为出射电子波函数的相移关于能量的导数.这一定义最早是针对电子在库仑场中的散射提出,后来人们将这一概念应用于光电离[23].Wigner 时间延迟意图描述电子在库仑场中运动的时候和其自由运动的时候时域性质的区别.值得注意的是在传统的量子力学中,电子在库仑场中的散射是定态问题(自由电子穿过势垒时候的透射和反射也是定态问题),而对于定态问题时间和坐标可分离变量,一般不讨论其时域性质,Wigner 时间延迟的提出可理解为对传统量子力学的扩展.
与前述中通过(8)式在隧穿出点处定义的响应时间相比,Wigner 时间延迟是一个思想量,其只能从测量得到的Wigner 相位中推导出来,而(8)式中仅包含基本的激光和原子的参数(参照(9)式),在知道这些基本参数情况下,可直接计算得到响应时间.此外,Wigner 时间延迟针对电子和核之间的两体相互作用提出,与系统吸收光子的实际时间无关[25];而(8)式定义的响应时间针对激光-电子-核之间的三体强相互作用提出,刻画了系统吸收光子的时间.再者,Wigner 时间延迟描述电子在库仑场中运动时库仑场对其运动的加速或者迟滞作用这一经典图像,而(8)式定义的响应时间包含电子在隧穿出点处从束缚态演化到连续态这一半经典的图像.
总之,目前针对光与物质相互作用的阿秒测量在理论上遇到了很多困难,对许多实验结果的解释存在很大争议,甚至得到了相反的结论,这些困难既有概念上的也有方法上的.概念上因为量子力学没有时间算符,定义量子系统的时间存在严峻挑战;方法上因为需要处理库仑-电子-外场三体相互作用,对其中复杂库仑效应的精确理论描述存在巨大挑战.强场原子电离响应时间理论方法的提出:1)在概念上,把光电效应中电子对光的响应时间明确定义为有经典对应的库仑-电子-外场三体强相互作用时间;2)在方法上,从系统对称性出发,通过引入位力定理和冲量定理在量子和经典的边界处理复杂的库仑效应;3)在应用上,该理论可定量重现近年来系列阿秒钟实验曲线,为不同实验提供了简单统一的物理图像.此外,该理论可被应用于不同形式的激光场(例如正交双色激光场)以量化动量分布的特征结构.再者,应用该理论得到了阿秒钟实验观测量的标度律公式,为更好理解阿秒钟在不同条件下的适用性及可行性提供系统的理论参考.最后,将该理论推广至分子体系,清晰地阐明了分子与原子系统阿秒钟动量分布偏转角差异的起源;并利用与响应时间密切相关的极性分子动量分布上下偏角的不对称性,分辨了极性分子亚周期内的固有偶极效应.响应时间理论模型展现了广泛的适用性和广阔的应用前景,有望成为阿秒测量中简洁精确的一般理论工具.
5 展 望
响应时间理论模型为研究量子经典边界处光电效应的响应时间问题提供了一个新视角.理论预言与实验结果的一致性支持了量子隧穿是瞬时的,而从量子过渡到经典的半经典过程需要一段有限的响应时间的论点.对响应过程的研究进一步指出量子转变为经典存在一个窄的时空边界,对应时间尺度大约100 as,空间尺度大约0.3 a.u.[43].从物理上来讲,光电效应通常涉及到电子从一个量子行为占主导的束缚态转变为一个经典行为主导的自由态.可以进一步设想对于弱光或者有关单光子跃迁中的光电效应如何定义量子与经典的边界并测量响应时间,是一个值得深入思考的问题.
另外,库仑导致的电离时间延迟(即电子的响应时间)对高次谐波辐射电子轨道的时域性质也具有重要影响[31],会导致谐波辐射电子轨道的出阱时间提前60 as,使其更靠近外场的峰值,进而导致短轨道(对应漂移时间更短的轨道)对谐波辐射的贡献增强了1 个数量级,且再散射电子的返回时间(对应谐波辐射时间)相应提前了30 as[53].这些影响本质上也是源于强场电离过程中电子波函数对于光场的响应,从而显著改变了电子轨道的时频性质.然而,到目前为止还没有理论能定量且高效描述这些影响.在强场隧穿电离响应时间理论的基础上进一步考虑再结合(散射)效应,从而将该理论推广至描述高次谐波辐射以及高阶阈上电离是接下来迫切需要展开的工作.此外,上述响应时间对电子轨道的重要影响也对高次谐波光谱学实验[17]提出了重要建议,即以往人们以不包含库仑效应的电子轨道为理论基础来设计“再散射电子轨道”重构方案,那么如果使用考虑库仑修正的电子轨道(包含响应时间)为基础,重构的结果将会如何? 此外,相关实验只是重构出了相对的电离和返回时间,对于绝对电离时间(与隧穿时间相关)和返回时间(对应谐波辐射时间)的重构将会更具有实际意义.再者,相较于原子和对称分子,极性分子高次谐波的辐射包含了更复杂的效应,如多中心干涉、核的振动拉伸以及奇偶谐波辐射等等.如何利用高次谐波光谱实现绝对时间的重构? 如何利用高次谐波实现分子再散射轨道的阿秒探测? 都是亟待解决的科学问题.
值得注意的是,强激光场作用下极性分子由于固有偶极的存在,在脉冲的前后半个周期将发生不对称电离现象[50,51].这一现象的产生是由于固有偶极导致的能级Stark 移动,使得电子在单个脉冲亚周期更倾向于从被缀饰向上的能级发生电离.一个有趣的想法就是,如果将极性分子发生不对称电离的相邻亚周期的电离净产量作为电流指标,那么就可以用极性分子作为一个最小尺度的“微观二极管”来研究阿秒响应的开关器件.这也符合当前晶体二极管(可将其称为经典二极管)在两极间加上正向电压时,二极管导通,加上反向电压时,二极管截止的特性.现如今计算机主板上的晶体二极管具有整流、检波、调频调制等重要作用,晶体二极管的开关时间,即晶体二极管对电信号的响应时间,是其性能的一个重要指标,通常为0.1—1.0 ns,这一时间很大程度上决定了计算机的工作速度.激光场作用下的极性分子通过隧穿电离发射电子,按照TRCM 理论,隧穿几乎是瞬时,仅在隧穿出点,电子从隧穿态过渡到电离态需要百阿秒的时间,根据这一机制,通过寻找适合的材质(例如二维材料),有望设计出巧妙利用隧穿效应的具有飞秒乃至亚飞秒响应时间的半经典二极管,而我们提出的TRCM 响应时间理论可为半经典二极管的设计提供简洁的理论工具.可以设想,如果用这种半经典二极管替换目前广泛使用的经典二极管,将会促进一种新型的“半经典计算机”的诞生.这种计算机一方面从计算效率和信息转换速度上相较于传统的电子计算机有飞跃式的提升;另一方面相较于全量子计算机,这种半经典计算机的可操作性更强、更易普及.
