低惯性与高惯性活性粒子混合体系中的相分离现象*
2023-10-30王晶焦阳田文得陈康
王晶 焦阳 田文得 陈康
(苏州大学物理科学与技术学院,软凝聚态物理及交叉研究中心,苏州 215006)
1 引言
活性物质[1−3]是一类可以从周围环境中获取能量来实现自主运动的物质.它们可以展现出独特的非平衡现象[4−10],例如巨大的密度涨落、动态斑图、相分离、涡旋等,因而在科学界备受关注.多数活性物质体系[11],如细菌、细胞、微泳体(microswimmer)、自驱动胶体粒子等,都处于高黏度的环境中,受到的流体阻力远大于粒子的惯性作用,研究者们大多采用过阻尼的模型来进行描述,如过阻尼的活性布朗粒子(active Brownian particles,ABP)模型[12−14].近年来,越来越多的研究者们开始关注惯性对活性物质运动的影响[15].这类物质处于低黏度的环境中,如振动的机器人[16]、Runner、飞行的昆虫以及微型飞行器.它们可以用欠阻尼的郎之万动力学模型来描述,也称为活性惯性粒子(active inertial particles,AIP)模型[17].
已有的研究结果表明,在一定的密度下,AIP系统中也可以发生相分离[17−20].但是,与ABP 系统相比,AIP 系统中惯性粒子之间具有强烈的碰撞反弹效应,不利于粒子的聚集[18−20],从而抑制相分离的发生.Dai 等[17]研究发现,惯性的存在导致体系中的团簇比较稀疏,并且在活性惯性团簇态和均匀无规则流体态之间存在一个较大的过渡区域,在该区域,粒子的局部密度很高,但没有形成六角密排.此外,在上述活性惯性粒子的体系中,尽管粒子的形状是各向同性的,但在相分离的稳态和均匀无规流体态之间依然出现了有趣的振荡行为,这一现象说明在活性团簇的内部存在动量转移的现象,这是惯性所诱导的集体运动.另外,Mandal 等[21]研究了ABP 系统和AIP 系统中粒子的热力学温度.在ABP 系统中,粒子的热力学温度没有明显的差别,但是在AIP 系统,活性团簇区域与均匀无规流体区域的粒子具有明显的热力学温差.这是由于在高密度的团簇区域,惯性粒子之间存在强烈的弹性碰撞,导致粒子将永远不会拥有沿其取向的速度;而在低密度的流体区域,粒子之间的碰撞较少,粒子可以持续加速,直到它们几乎都达到自身的驱动速度va.因此,就粒子的动力学温度而言,团簇区是“冷”的,流体区是“热”的.
在现实情况下,活性物质的生存环境比较复杂[22−26],许多体系中物质的种类并不是单一的,而是由多种成分混合而成.少数关于活性物质混合体系的研究表明,体系的成分及其比例会对相分离产生影响.在活性与非活性粒子的混合体系[27]中,研究者们发现,这种混合体系不利于活性诱导的相分离现象的产生,体系中形成的团簇在边缘是活性的,内部是非活性的.与单一体系相比,团簇的分裂与融合比较频繁.在低活性与高活性粒子混合体系的模拟[28]研究中,当两种粒子的活性差较大时,在致密的团簇内部可以观察到高速区域和低速区域.与高速粒子和低速粒子的单一体系相比,高速粒子进入致密相受到抑制,而低速粒子进入致密相得到促进,随着低速粒子活性的增加,这些影响逐渐减弱.在活性粒子和非活性棒状粒子混合体系的模拟[29]研究中,研究者们发现该体系中也可以发生相分离,但是由于棒状粒子的形状各向异性,导致体系的相分离能力较弱,形成的团簇比较稀疏.受上述研究的启发,构建了一个二元混合体系,该体系由低惯性和高惯性的两种活性粒子组成.感兴趣的是,与单一的低惯性活性粒子体系或高惯性活性粒子体系相比,混合体系中的相分离现象是更容易发生还是会被抑制? 这一研究将为我们在复杂环境下调控活性物质的集体行为提供基础[30,31].
本文通过郎之万动力学模拟,首先研究了单个活性惯性粒子的运动行为(补充材料1 (online)).结果表明,单粒子的运动行为由粒子运动的惯性特征时间(τI=m/ζ)和活性力的弛豫时间(1/Dr)共同决定.然后研究了低惯性和高惯性活性粒子混合体系中的相分离现象.研究发现,与单一组分的低惯性粒子体系或高惯性粒子体系相比,中等密度的混合体系有利于相分离现象的发生,而高密度的混合体系不利于相分离的发生.此外,在混合体系中,两种粒子的比例对体系的相分离程度起着至关重要的影响.在大量低惯性粒子与少量高惯性粒子组成的混合体系中,由于受到高惯性粒子的撞击,低惯性粒子的速度增大,这有利于相分离现象的产生.但是随着高惯性粒子比例的增大,高惯性粒子与高惯性粒子之间的弹性碰撞占据主导地位,这种激烈的碰撞会抑制相分离现象.
2 体系与模型
通过郎之万动力学模拟研究了二元混合体系中的相分离现象.二元混合体系由N1个低惯性粒子和N2个高惯性粒子组成,体系中的总粒子数为N,N=N1+N2.两种粒子的直径均为σ(图1(b)).所有粒子之间的相互作用遵循纯排斥的Weeks-Chandler-Anderson (WCA) 势,其表达式为
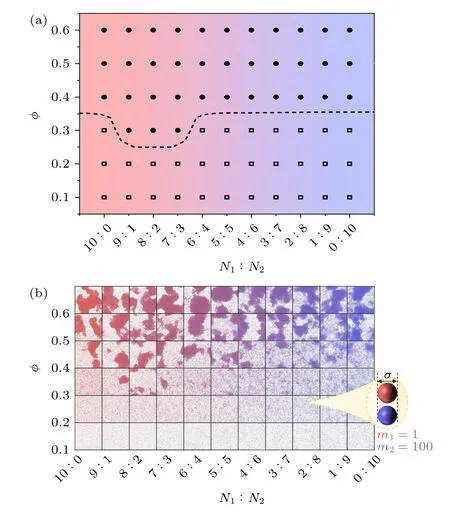
图1 (a)模拟相图,黑色空心正方形代表均匀无规流体相,黑色实心圆形代表均匀无规流体与团簇的共存相,黑色虚线表示两相的相边界,背景颜色代表混合体系中的粒子组分比(颜色与模拟相图相对应);(b)快照相图,粒子的颜色代表其质量(红色粒子为低惯性粒子,蓝色粒子为高惯性粒子)Fig.1.(a) Simulated phase diagram,the black hollow square represents the homogeneous random fluid phase,the black solid circle represents the coexisting phase of the homogeneous random fluid and the cluster,the black dashed line represents the phase boundary of the two phases,which is divided according to the local density distribution,the background color represents the particle composition ratio in the mixing system,and the color is corresponding to the simulated phase diagram;(b) phase diagram of snapshoots,the color of particles represents their mass,the red particles are low inertia particles,and the blue particles are high inertia particles.
其中ε为相互作用强度,r为两粒子之间的距离,rc=21/6σ为相互作用势的截断距离.粒子的运动遵循郎之万动力学方程,表达式为
其中ri和Ui分 别是第i个粒子的位置矢量和总势能.ζ为平动摩擦系数,kBT为标度温度.所有粒子自驱动力(活性力)的大小均相同,为Fa.粒子自驱动速度的大小也相同,为va=Fa/ζ.但自驱动速度的方向是独立的,第i个粒子的自驱动方向为uˆi=(cosθi,sinθi),其中θi为粒子取向与x轴之间的夹角.自驱动方向变化的快慢由旋转扩散系数Dr所决定,1/Dr代表粒子定向驱动的持久时间.ηi(t)和ξi(t) 为单位方差的高斯白噪声.方程(2)描述了粒子在平动自由度上的运动,方程(3)描述了粒子自驱动方向的耦合旋转动力学.
本文使用约化单位,以m1,σ和ε作为质量、长度和能量的基本单位.因此,时间单位为τ=,速度单位为σ/τ,力的单位为ε/σ.在模拟中,设置ζ=10,Fa=10,kBT=1,Dr=0.001.低惯性粒子的质量为m1,高惯性粒子的质量为m2=100(m2=100m1).粒子的质量决定粒子运动的惯性特征时间τI=m/ζ和惯性特征长度lI=τIva.模拟盒子采用周期性的边界条件,其大小为LxLy=200σ×200σ.体系中粒子的面密度为ϕ=Nπσ2/(4LxLy).
3 结果与讨论
3.1 相图与机制
研究不同组分比例(N1:N2)下,低惯性和高惯性活性粒子混合体系中的相分离现象.图1(a)中的相边界是依据粒子局部密度和格点局部密度判断的(具体内容见3.2 节).在低密度(ϕ=0.1)的情况下,单一组分的低惯性粒子体系(N1:N2=10:0)、高惯性粒子体系(N1:N2=0:10)以及两种粒子组成的混合体系均呈现均匀无规流体态(图1).在中等密度(ϕ=0.3)下,单一组分的体系呈现均匀无规流体态;然而,在大量低惯性粒子和少量高惯性粒子组成的混合体系中却出现了明显的相分离现象,这说明该组分比例有利于粒子的聚集.在高密度(ϕ≥0.4)的情况下,单一组分的体系和混合体系中都可以产生宏观相分离现象.
为了探究相分离现象发生的物理机制,通过最简单的粒子对碰撞模型研究了活性惯性粒子间的碰撞(补充材料2−4 (online)).当两个低惯性粒子发生碰撞(图2(a))后,粒子会在排斥力的作用下分开一定的距离,但不会立即远离,粒子相互远离所用的时间由活性力的弛豫时间(1/Dr)决定.如果在此时间内,有其他粒子靠近、并包围粒子对,则这些粒子就会在该位置形成聚集.当两个高惯性粒子发生碰撞(图2(c))后,由于强烈的弹性碰撞,粒子对迅速分离,较难形成聚集.当低惯性粒子与高惯性粒子发生碰撞(图2(b))后,低惯性粒子由于受到强烈的撞击,迅速改变运动方向,而高惯性粒子的运动方向几乎保持不变.
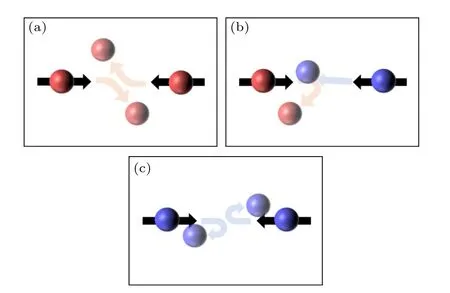
图2 粒子碰撞示意图.红色球表示质量为 m1 的低惯性粒子,蓝色球表示质量为 m2 的高惯性粒子,深色球表示碰撞前的粒子,浅色球表示碰撞后的粒子,黑色箭头表示碰撞前粒子的运动轨迹,浅红色箭头表示碰撞后低惯性粒子的运动轨迹,浅蓝色箭头表示碰撞后高惯性粒子的运动轨迹Fig.2.Schematic diagram of collisions between particles,the red spheres represent low inertia particles with m1,the blue spheres represent high inertial particles with m2,the dark spheres represent the particles before the collision,the light spheres represent the particles after the collision,the black arrows represent the trajectory of the particles before the collision,the light red arrows represent the trajectory of the low inertia particles after the collision,the light blue arrows represent the trajectory of the highly inertial particles after the collision.

图3 (a),(b)分别为图(c)中团簇内外所选区域的沃罗诺伊图(红色粒子为低惯性粒子,蓝色粒子为高惯性粒子);(c)模拟快照(N1 :N2=8:2,ϕ=0.6);(d)图(c)所对应的粒子沃罗诺伊单元的面积 Sn ;(e) 图(c)所对应的格点局部密度 ϕ(i,j),图中颜色代表格点 (i,j)的密度Fig.3.(a),(b) Voronoi diagrams of cluster region and gas region in panel (c),respectively (Red particles are the low inertia particle,and the blue particles are the high inertia particle);(c) simulation snapshot (N1 :N2=8:2,ϕ=0.6);(d) area Sn of the Voronoi unit of the particle corresponding to panel (c);(e) lattice local density ϕ(i,j) corresponding to panel (c);the color in the figure represents the density of the lattice (i,j).
在低惯性粒子与高惯性粒子组成的混合体系中,这3 种碰撞都会发生.并且,随着粒子组分比例(N1:N2)的变化,这3 种碰撞发生的概率也会随之变化.中等密度(ϕ=0.3)下,在大量低惯性粒子和少量高惯性粒子组成的混合体系中,高惯性粒子与低惯性粒子之间的碰撞会使得低惯性粒子的速度增大,从而导致低惯性粒子与低惯性粒子的碰撞概率增大,有利于粒子的聚集,促进相分离现象的产生.而在少量低惯性粒子和大量高惯性粒子组成的混合体系中,高惯性粒子间强烈的弹性碰撞占主导地位,使得高惯性粒子的速度较低,难以诱导低惯性粒子产生聚集.在高密度(ϕ=0.6)的混合体系中,低惯性粒子的减少与高惯性粒子的增加(N1:N2减小)依然不利于相分离现象的发生(图5(b)).
3.2 结 构
体系中是否发生相分离是根据粒子局部密度分布P(ϕn) 和格点局部密度分布P(ϕ(i,j)) 判断的.首先计算粒子的局部密度分布P(ϕn),计算方法如下.根据二维平面上粒子的位置得到沃罗诺伊图(Voronoi diagram),图中包含多个沃罗诺伊单元,每个单元中仅包含一个粒子,并且该单元内任意一点到该粒子的距离比到其他粒子的距离都要近.另外,在划分沃罗诺伊单元之前,需要将模拟区域内边界附近的粒子(粒子距离模拟平面边界的垂直距离Ladd≤10)复制到模拟区域的外侧,使得模拟区域内边界附近粒子的沃罗诺伊单元满足周期性边界条件.Sn表示第n个粒子所在沃罗诺伊单元的面积.ϕn表示第n个粒子的粒子局部密度,表达式为
在中等密度(ϕ=0.3)下,单一组分的低惯性粒子体系和高惯性粒子体系的粒子局部密度分布P(ϕn)均呈现单峰状(图4(a)),表明体系处于均匀无规流体态.然而,在N1:N2=9:1 和N1:N2=8:2 的混合体系中,粒子局部密度分布P(ϕn) 呈现双峰状,表明体系处于均匀无规流体与团簇的共存态.这说明,与单一组分的体系相比,中等密度的混合体系有利于相分离现象的发生.并且,P(ϕn)第1 个峰(代表低密度的气态区域)的峰值较高,第2 个峰(代表高密度的团簇区域)的峰值较低.这表明在发生相分离的混合体系中,少量粒子形成聚集,而大量粒子仍然处于气态区.在高密度(ϕ=0.6)的情况下,与低惯性或高惯性的体系相比,混合体系中P(ϕn) 的第2 个峰值较低(图4(b)),这说明高密度的混合体系会抑制相分离现象的发生.
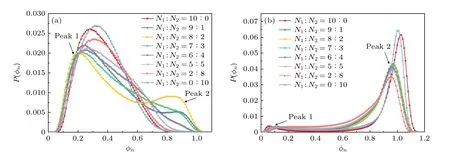
图4 中等密度和高密度体系中的粒子局部密度分布 P(ϕn),Peak 1,Peak 2 分别表示混合体系(N1 :N2=8:2)中粒子局部密度分布 P(ϕn) 的第1 个峰和第2 个峰 (a) ϕ=0.3;(b) ϕ=0.6Fig.4.Local density distribution P(ϕn) of particles in the system with medium density (a) and high density (b).Peak 1 and Peak 2 represent the first and second peaks of local density distribution P(ϕn) of particles in the mixed system of N1 :N2=8:2,respectively: (a) ϕ=0.3;(b) ϕ=0.6.
在中等密度(ϕ=0.3)的体系中,粒子局部密度分布P(ϕn) 可以很好地反映体系的相分离程度.但是,在高密度(ϕ=0.6)的体系中,由于气态区域的粒子数量稀少,P(ϕn) 的第一个峰较低,导致P(ϕn) 较难全面反映粒子比例(N1:N2)的变化对相分离的影响.所以,进一步计算了格点局部密度分布P(ϕ(i,j)).该分布是在沃罗诺伊图的基础上,将二维模拟平面划分为 1σ×1σ的格点单元.格点(i,j)的密度为
其中,wn为格点 (i,j) 与沃罗诺伊单元相交区域的面积.因此,P(ϕ(i,j)) 代表空间权重的密度分布,而P(ϕn) 代表粒子权重的密度分布.在中等密度(ϕ=0.3)、N1:N2=8:2 的混合体系中,与粒子局部密度分布P(ϕn)类似,格点局部密度分布P(ϕ(i,j))也呈现双峰状(图5(a)),但其第2 个峰的峰值较低,表明体系中形成的团簇较小.在高密度(ϕ=0.6)的体系中,格点局部密度分布P(ϕ(i,j))呈现双峰状(图5(b)),双峰分别代表局部密度低的气态区域和局部密度高的团簇区域(图3(e)).与单一组分的体系相比,混合体系中P(ϕ(i,j)) 的双峰由两侧向中间位置移动,这说明混合体系不利于相分离现象的发生.

图5 中等密度和高密度体系中的格点局部密度分布 (a) ϕ=0.3;(b) ϕ=0.6Fig.5.Local density distribution of lattices in the system with medium density and high density: (a) ϕ=0.3;(b) ϕ=0.6.
由沃罗诺伊图可知,在高密度的团簇内部,粒子沃罗诺伊单元的面积很小(图3(a)),且形状为规则的正六边形,表明团簇内部粒子有序排列.然而,在低密度的气态区域,粒子沃罗诺伊单元的面积很大(图3(b)),且形状不规则,表明气态区域的粒子无规排列.根据这一特点,计算了近邻粒子数分布P(bn).bn为第n个粒子所在沃罗诺伊单元的顶点个数,也称为近邻粒子数.由近邻粒子数分布P(bn)可知,在中等密度(ϕ=0.3)下,近邻粒子数为bn=6的粒子比略高于bn=5和bn=7 的粒子(图6(a)).这表明,在中等密度下,体系中形成的团簇较小,缺陷较多.并且,与单一组分的体系相比,在大量低惯性粒子与少量高惯性粒子组成的混合体系中团簇内部粒子的排列更加密集.这说明,中等密度下,少量高惯性粒子的存在可以诱导低惯性粒子产生聚集,进而发生相分离.在高密度(ϕ=0.6)下,体系中都可以发生相分离,形成致密的大团簇.然而,与单一组分的体系相比,混合体系不利于相分离现象的发生(图6(b)).这是因为,在高密度下,混合体系的团簇内部,高惯性粒子与低惯性粒子之间的碰撞较为频繁,使得团簇容易分裂,从而抑制相分离现象的发生.

图6 中等密度和高密度体系中的近邻粒子数分布 (a) ϕ=0.3;(b) ϕ=0.6Fig.6.Neighbor particle population distribution in the system with medium density and high density: (a) ϕ=0.3;(b) ϕ=0.6.
局部密度分布和近邻粒子数分布一致表明,大量低惯性粒子和少量高惯性粒子组成的混合体系有利于相分离现象的产生,而少量低惯性粒子和大量高惯性粒子组成的混合体系则不利于相分离现象的产生.为了明确这一现象产生的原因,分别计算了混合体系中两种粒子的局部密度分布P(ϕn)、粒子局部密度分布的平均值以及近邻粒子类型之比.的表达式为
在ϕ=0.3,N1:N2=8:2 的混合体系中,两种粒子的P(ϕn) 均呈现双峰状,并且,与高惯性粒子相比,低惯性粒子第2 个峰的峰值较高(图7(a)).这说明,在该混合体系中低惯性粒子更容易形成聚集.随着高惯性粒子比例的增多,两种粒子的P(ϕn)均呈现单峰状(图7(b)),说明体系为低密度的均匀无规流体态.在高密度(ϕ=0.6)的混合体系中,两种粒子的P(ϕn) 均呈现双峰状,随着高惯性粒子比例的增多,第2 个峰的峰值向左移动,粒子局部密度的平均值减小(图7(d)).这说明高惯性粒子的增多不利于相分离的形成.这是因为高惯性粒子的增加使得体系中粒子的碰撞更加激烈,团簇的分裂与融合更加频繁(补充材料5 (online)).

图7 中等密度和高密度的体系中,两种粒子的粒子局部密度分布 P(ϕn) 及粒子局部密度的平均值 .红色表示低惯性粒子;蓝色表示高惯性粒子;黄色表示体系中的所有粒子 (a),(c) ϕ=0.3;(b),(d) ϕ=0.6Fig.7.Local density distribution P(ϕn) and the average of the local density of the particles with different inertias in the system with medium density and high density.Red represents low inertial particles;the blue represents high inertial particles;the yellow represents all particles in the system: (a),(c) ϕ=0.3;(b),(d) ϕ=0.6.
如前所述,在混合体系中,两种粒子的粒子局部密度分布P(ϕn) 和粒子局部密度分布的平均值表现出了明显的差异.因此,进一步研究了两种粒子近邻粒子类型的差异.近邻粒子的判断依据为: 两粒子的沃罗诺伊单元共用同一条边.如图8所示,n1,N1表示编号为n1的低惯性粒子周围出现低惯性粒子(N1),即同类粒子近邻;n1,N2则表示编号为n1的低惯性粒子周围出现高惯性粒子(N2),即异类粒子近邻.同理,n2,N1表示异类粒子近 邻,n2,N2表示同类粒子近邻.在中等密度(ϕ=0.3)下,与混合体系中的粒子组分比例相比,在大量低惯性粒子与少量高惯性粒子组成的混合体系中,高惯性粒子周围出现同类粒子的概率较高,而低惯性粒子周围出现异类粒子的概率较高(图8(a)).这是因为,在这些混合体系中高惯性粒子的比例较低,扩散能力较强,并且高惯性粒子与低惯性粒子之间的碰撞使得低惯性粒子速度增加,有利于相分离现象的产生.然而,在高密度(ϕ=0.6)下,两种粒子周围出现同类粒子或异类粒子的概率等于体系中两种粒子的比例,即两种粒子均匀混合(图8(b)).这说明密度的增大使得高惯性粒子的扩散能力减弱,难以诱导低惯性粒子形成聚集.
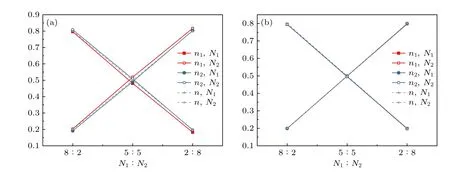
图8 中等密度和高密度的体系中,粒子的近邻粒子类型之比,纵轴表示粒子周围出现同类(或异类)粒子的概率p.红色实心正方形表示低惯性粒子附近出现低惯性粒子的概率,红色空心正方形表示低惯性粒子附近出现高惯性粒子的概率;蓝色实心圆形表示高惯性粒子附近出现低惯性粒子的概率,蓝色空心圆形表示高惯性粒子附近出现高惯性粒子的概率;灰色实心三角形和空心三角形分别表示体系中低惯性粒子和高惯性粒子占总粒子数的比值 (a) ϕ=0.3;(b) ϕ=0.6Fig.8.Ratio of the particle’s nearest neighbor particle types in the system with medium density and high density,and the vertical axis shows the probability p of similar (or dissimilar) particles occurring around the particle.Red solid square indicates the probability of low inertial particles near the low inertial particles,and the red hollow square indicates the probability of high inertial particles near the low inertial particles.Blue solid circle indicates the probability of low inertial particles near high inertial particles,and blue hollow circle indicates the probability of high inertial particles near high inertial particles.Gray solid and hollow triangle represent the ratio of low and high inertial particles to the total number of particles in the system,respectively: (a) ϕ=0.3;(b) ϕ=0.6.
为了量化相分离体系中团簇的大小,计算了团簇尺寸分布P(n) 和平均畴尺寸ℜ.畴尺寸的表达式为
其中S(k) 为静态结构因子,
k=(kx,ky) 为波矢量,其分向量为:kx=mΔkx,ky=mΔky,m,n=0,±1,±2,±3,···(m和n不同时为0).对于周期性边界的二维平面(Lx=200,Ly=200)上的模拟,波矢量的增量可以设置为 Δkx=2π/Lx,Δky=2π/Ly,波矢量在kcut=(π,π) 处截断.在团簇尺寸分布P(n) 的计算中,团簇的判断依据为:当两个粒子之间的距离小于截断距离时,判定两粒子归属于同一团簇.我们发现,团簇的尺寸分布P(n) 可以很好地用指数截断n0的密率分布[32,33]来描述:p(n)/p(1)=.
如图9(a)所示,在ϕ=0.3,N1:N2=8:2 的混合体系中,δ ≈3,团簇的尺寸达到最大,平均畴尺寸也达到最大(图9(c)),这与前文的计算结果相吻合.在高密度(ϕ=0.6)的情况下,P(n) 第2 个峰的峰值都比较高,表明体系中均可形成大团簇(图9(b)).然而,随着高惯性粒子比例的增大,平均畴尺寸ℜ减小.这说明高惯性粒子的增加会引起体系中更加强烈的弹性碰撞,使得大团簇比较稀疏,平均畴尺寸较小.
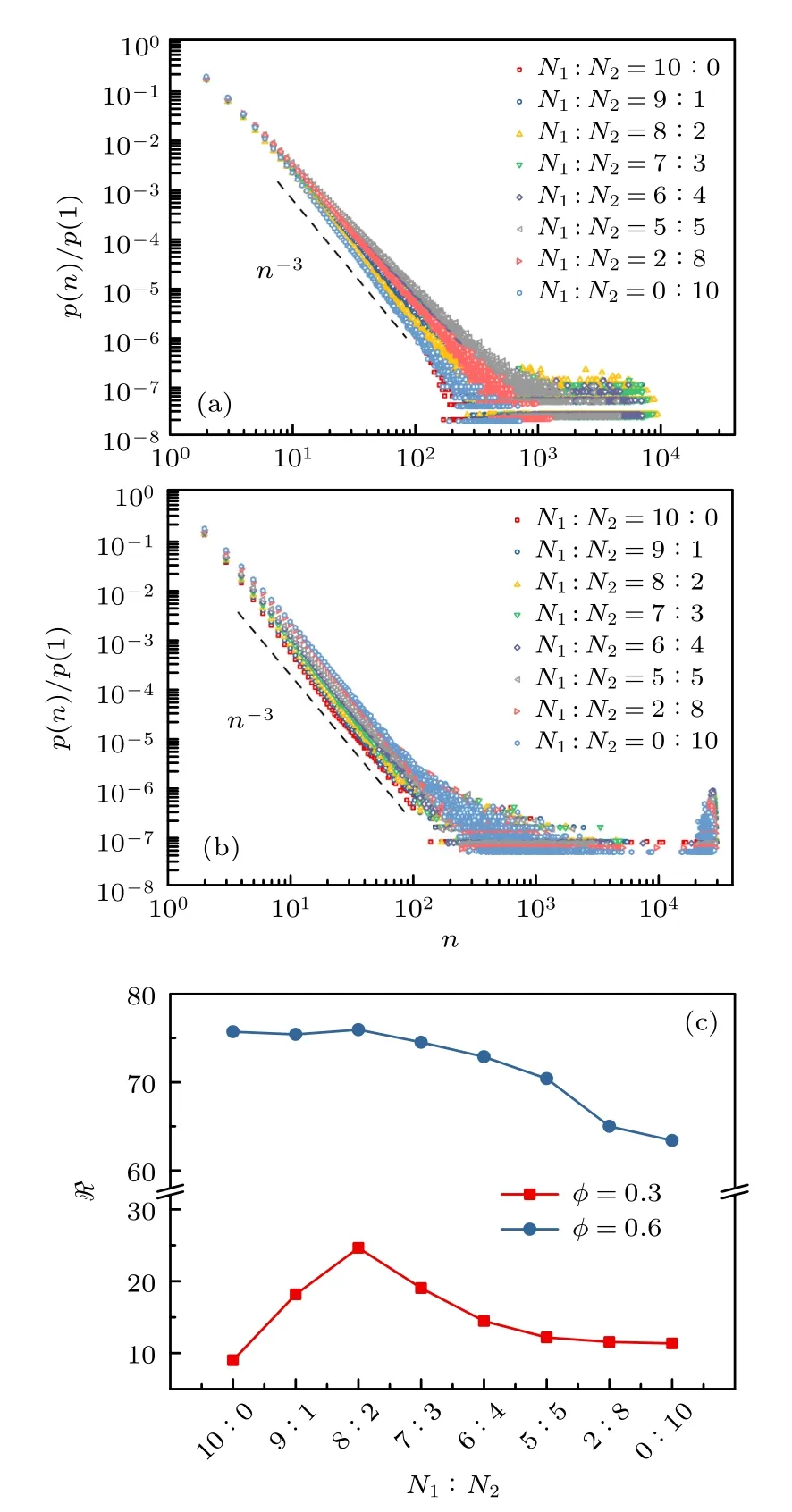
图9 中等密度(a)和高密度(b)的体系中,团簇的尺寸分布 P(n) ;(c)平均畴尺寸ℜFig.9.Size distribution P(n) of clusters in the system with medium density (a) and high density (b);(c) average domain size ℜ.
为了解混合体系中两种粒子在团簇区域和气态区域的分布情况,计算了两区域中的粒子类型之比.团簇(cluster)区域和气态(gas)区域的判断依据为: 对于编号为i的粒子,若i粒子所属团簇中的粒子个数大于1000,则i粒子位于cluster 区域;否则,i粒子位于gas 区域.nc表示cluster 区域中的粒子个数,ng表示gas 区域中的粒子个数(ng=N -nc).如图10 所示,在中等密度(ϕ=0.3)和高密度(ϕ=0.6)下,与混合体系中的粒子比例相比,在cluster 区域两种粒子的比例(n1/nc:n2/nc)较高;而在gas 区域两种粒子的比例(n1/ng:n2/ng)较低.这说明在高密度的cluster 区域,低惯性粒子较多;而在低密度的gas 区域,高惯性粒子较多.并且,随着高惯性粒子的增加,这种现象更加明显.这说明在混合体系中,少量高惯性粒子的存在,会使得低惯性粒子的速度增大,有利于低惯性粒子与同类粒子发生碰撞,从而形成聚集.但是,当高惯性粒子的数量较多时,高惯性粒子与同类粒子之间的弹性碰撞占主导地位,不利于形成团簇.总之,在大量低惯性粒子和少量高惯性粒子组成的混合体系中,少量高惯性粒子的存在有利于相分离现象的发生;而在少量低惯性粒子和大量高惯性粒子组成的混合体系中,高惯性粒子间的弹性碰撞会抑制相分离现象的形成.

图10 中等密度和高密度的体系中,cluster 区域和gas 区域中的粒子类型之比(红色代表cluster 区域,蓝色代表gas 区域,灰色代表整个混合体系) (a) ϕ=0.3;(b) ϕ=0.6Fig.10.Ratio of particle types in the cluster and gas regions in the system with medium density and high density(The red represents the cluster region,blue represents the gas region,and gray represents the whole mixed system):(a) ϕ=0.3;(b) ϕ=0.6.
3.3 动力学
综上所述,在低惯性和高惯性活性粒子的混合体系中,粒子组分比对体系的相分离程度起着至关重要的影响.在中等密度下,大量低惯性粒子和少量高惯性粒子组成的混合体系中,少量高惯性粒子的存在有利于低惯性粒子的聚集,从而发生形成相分离;然而,当高惯性粒子的比例增大后,相分离会被破坏.为进一步了解混合体系中相分离现象产生和破坏的原因,计算了粒子的平均热力学温度,该温度通过粒子的平均动能来定义,(v为粒子瞬时速度的大小).低惯性粒子在cluster 区域和gas 区域中的平均热力学温度分别为
高惯性粒子在cluster 区域和gas 区域中的平均热力学温度分别为
如图11(b)所示,在中等密度(ϕ=0.3)下,与单一组分的低惯性粒子体系相比,在大量低惯性粒子和少量高惯性粒子组成的混合体系中,gas 区域低惯性粒子的平均热力学温度较高.这说明,高惯性粒子的存在使得低惯性粒子的速度增加,热力学温度升高,进而导致低惯性粒子与低惯性粒子的碰撞概率增加,有利于形成聚集.随着低惯性粒子的减少和高惯性粒子的增加,在cluster 区域出现了明显的高温区域和低温区域(图11(a)),并且团簇会在高温区域发生分裂(补充材料6 (online)),这一现象与单一组分的高惯性粒子体系类似.这说明,在少量低惯性粒子和大量高惯性粒子组成的混合体系中,高惯性粒子与高惯性粒子之间的弹性碰撞占据主导地位,导致团簇极其不稳定,容易在局部温度较高的区域发生分裂.在高密度(ϕ=0.6)下,随着粒子组分比的减小,低惯性粒子在gas 区域的速度不断减小.这说明在高密度的混合体系中,高惯性粒子的碰撞较为激烈,难以诱导低惯性粒子产生聚集,不利于相分离现象的发生.

图11 (a)热力学温度相图,粒子颜色代表其热力学温度Teff ;(b),(c) cluster 区域和gas区域中粒子的平均热力学温度,低惯性粒子的热力学温度参照左侧刻度线,高惯性粒子的热力学温度参照右侧刻度线Fig.11.(a) Thermodynamic temperature phase diagram,in which the color of particle represents its thermodynamic temperature Teff ;(b),(c) the mean thermodynamic temperatures of the particles in the cluster and gas regions,in panels (b) and (c),the thermodynamic temperature of low inertia particles is based on the left scale line,and the thermodynamic temperature of high inertia particles is based on the right scale line.
4 结果与讨论
通过郎之万动力学模拟研究了低惯性活性粒子与高惯性活性粒子组成的混合体系中的相分离现象.研究发现,混合体系的相分离程度与粒子比例和系统密度ϕ有关.在中等密度(ϕ=0.3)下,与单一组分的体系相比,混合体系有利于相分离现象的发生.特别是,在大量低惯性粒子与少量高惯性粒子的混合体系中发生了明显的相分离现象,形成了较大的团簇.在团簇(cluster)区域,两种粒子的比例(n1/nc:n2/nc)高于混合体系的比例,而在低密度的气态(gas)区域,两种粒子的比例(n1/ng:n2/ng)低于混合体系的比例.这是因为,在这种混合体系中,高惯性粒子的比例较低,高惯性粒子与同类粒子之间的碰撞较少,粒子速度较大,扩散能力较强;与此同时,高惯性粒子与低惯性粒子之间的碰撞使得低惯性粒子的速度增加,有利于低惯性粒子与同类粒子形成聚集.而当高惯性粒子的比例增加后,高惯性粒子与同类粒子之间的弹性碰撞增多,难以诱导少量低惯性粒子发生聚集.在高密度(ϕ=0.6)下,与单一组分的体系相比,混合体系不利于相分离现象的发生,体系中的团簇较为稀疏.并且,随着混合体系中粒子比例的减少,惯性粒子之间的弹性碰撞更加激烈,使得团簇的分裂与融合变得更加频繁.
关于活性惯性粒子的已有研究表明,惯性的增大不利于相分离现象的发生.然而,本文研究发现,在中等密度的混合体系中,少量高惯性粒子的存在有利于相分离现象的发生.这说明活性惯性粒子的混合体系可以产生新颖的动力学现象,并且该模拟研究在实验中可以利用3D 打印的微型振动机器人实现.在本研究中,只改变了体系密度和两种惯性粒子的组分比例.除此之外,体系中还有一些值得探索的物理参数,例如,两种粒子活性力的相对大小、粒子质量的相对大小等.在后续的研究工作中,我们将调控这些参数,对活性惯性粒子的混合体系进行更加深入的探究.总之,对活性物质混合体系的研究不仅有助于我们理解同一环境中多种活性物质的集体行为,也有望被应用于新型材料的设计与控制.
