4K大冷量GM型脉冲管制冷机*
2023-10-30刘旭明潘长钊张宇廖奕郭伟杰俞大鹏
刘旭明 潘长钊† 张宇 廖奕 郭伟杰 俞大鹏
1) (南方科技大学量子科学与工程研究院,深圳 518055)
2) (深圳国际量子研究院,深圳 518048)
1 引言
液氦温区GM 型制冷机是一种可以在4 K 提供数百毫瓦或更高制冷量的机械制冷技术,广泛用于凝聚态物理、量子计算、低温科学仪器、超导及军工等领域[1-3].相较于GM 制冷机,GM 型脉冲管制冷机由于冷指完全无运动部件,具有低振动、长寿命和高可靠性等突出优点,正在逐步取代GM 制冷机,成为在液氦温区实际应用最广泛的商用制冷机,且其在一些对振动要求极为严苛的场合具有重要而不可替代的应用.
GM 型脉冲管制冷机于1963 年由Gifford 和Longsworth[4]首次提出,但由于脉冲管制冷机的最低温度与当时的GM 制冷机相比没有优势,且制冷效率极低,在此后的20 多年里并没有引起足够的关注和重视[5].直到20 世纪90 年代,随着低温高比热磁性蓄冷材料的发展应用以及脉冲管调相机构的不断革新,GM 型脉冲管制冷机开始获得液氦温度,并在液氦温区不断突破其制冷性能[6-9].值得一提的是,Chen 等[10-12]在国内率先开展了液氦温区GM 型脉冲管制冷机的研究,他们在研究过程中相继提出了“第二小孔”和“双小孔”的调相机构,这些机构也起到了引入DC 直流的作用.Cheng 等[13,14]也曾开展过两级气耦合GM 型脉冲管制冷机的研究,但最终仅获得了8.9 K 的最低温度.进入21 世纪,液氦温区GM 型脉冲管制冷机研究主要集中在“如何获取更低的制冷温度”[15]、“如何实现更大的制冷量”[16,17],以及“如何实现更轻量化的装置”[18,19]这3 个方向发展.目前,美国Cryomech 公司和日本Sumitomo 公司已经推出了一系列GM 型脉冲管制冷机型号产品,功耗通常在6.5—13.7 kW 之间,最低温度在2.8 K 附近,可在4.2 K 提供0.5—2.7 W 不等的制冷量[20,21].
截至目前,商用液氦温区GM 型脉冲管制冷机的制冷量已经与GM 制冷机性能相当,但其最低温度和制冷效率仍低于GM 制冷机[20,21].对于往复交流振荡的回热式制冷系统,工质气体质量流与压力波之间存在的相位差极大地影响系统的制冷性能.相比GM 制冷机依靠电机驱动排出器实现任意所需的相位调节,GM 型脉冲管制冷机使用“双向进气+小孔气库”或“四阀”等调相机构以被动改变系统热端工质气体阻抗的方式,来间接实现系统冷端工质气体的相位调节.因此,脉冲管制冷机调相机构的高效调节是保证制冷机能够获得液氦温度和有效提高制冷性能的关键[8].
先前有关GM 型脉冲管制冷机调相机构的研究,大多集中在制冷机获得液氦温度之后单个调相元件对低温级制冷性能的影响方面[22-27].而目前传统液氦温区GM 型脉冲管制冷机用来调节相位的阻力元件至少有4 个,并且系统由于采用两级气耦合的结构形式,制冷机预冷级和低温级必须在同一工况下运行,两级之间存在着复杂的耦合影响,调节时往往牵一发而动全身[28].实验过程中可能要花费大量时间,并且很难找到所有元件对应的最佳开度以使制冷机获得液氦温区温度.综上,目前液氦温区GM 型脉冲管制冷机研究,未见对制冷机获取液氦温度的调节优化过程、以及多个调相元件之间的相互耦合影响展开深入研究.
针对上述问题,本文基于Sage 软件设计并构建了双向进气型气耦合两级GM 脉冲管制冷机整机仿真模型,计算了一、二级小孔和一、二级双向分别对两级制冷温度的影响,分析了4 个调相元件各自之间的相互耦合影响,给出制冷机获取液氦温区温度的调节优化过程.在此基础上,成功研制制冷机实验样机.该研究有助于打破国外技术封锁,为凝聚态物理、材料、医学等前沿基础科学研究提供重要支撑.
2 理论模型及系统结构
2.1 理论模型
本文数值计算主要基于Sage 软件.针对气体工质,从积分形式的N-S 方程出发,Sage 通过三大守恒方程交替连接各个模块化部件,即可实现对回热式制冷系统的整机模拟和仿真[29].
连续性方程:
动量方程:
能量方程:
式中,ρ和u分别为工质气体的密度(kg/m3)和速度(m/s);A为流通截面积(m2);P为压力(Pa);F为黏性压力梯度项;e为比总自由能;Qw为单位轴向距离热流量(W);q为轴向瞬态热流密度(W/m2).其中,
式中,dh为水力直径(m),K为当地损失系数,L为总长度(m),k为工质气体的热导率(W/(m·K));SX为湿周(m);Tw和T分别表示固体壁面和气体的平均温度(K).对于不同部件,Sage 采用不同的经验公式来计算(4)式—(6)式中所涉及的流动阻力系数f、努塞尔数Nu和轴向热导率优化算子Nk等.
基于制冷机真实结构构建理论模型,依次设定系统的初始条件、节点参数和几何参数,Sage 进行迭代计算收敛后即可得到各个离散节点的计算结果,比如温度、压力、质量流等瞬时值.因为在GM循环中,内部压力波已经偏离热声学中正弦波的特性,上述波动值在Sage 中可通过傅里叶级数的形式表达如下.
温度、压力和质量流的表达式分别为
这里,T0,P0和分别为系统的平均温度(K)、平均压力(Pa)和DC 直流量(kg/s);Tn,Pn和分别为温度(K)、压力(Pa)和质量流的第n阶幅值(kg/s);αT,n,αp,n和分别为温度、压力和质量流的第n阶相位(rad).最高阶N值与系统的时间节点有关.
对上述数据进行处理,即可得到系统任意位置所需的物理量.
式中,ε为回热器的填充孔隙率;kg和ks分别表示工质气体和蓄冷材料的热导率(W/(m·K)).
2.2 制冷机结构
图1 为本文所研制的GM 型脉冲管制冷机的基本结构.其中,0 表示压力波发生系统,01 为压缩机,02 为旋转阀;1 表示脉冲管预冷级(第1 级)制冷系统,11 为预冷级回热器热端换热器,12 为预冷级回热器,13 为预冷级回热器冷端换热器,14 为预冷级脉冲管冷端导流器,15 为预冷级脉冲管,16 为预冷级脉冲管热端导流器,17 为预冷级气库,18 为预冷级双向进气,19 为预冷级小孔阀.2 表示脉冲管低温级(第2 级)制冷系统,21 为低温级回热器热端换热器,22 为低温级回热器,23 为低温级回热器冷端换热器,24 为低温级脉冲管冷端导流器,25 为低温级脉冲管,26 为低温级脉冲管热端导流器,27 为低温级气库,28 为低温级双向进气,29 为低温级小孔阀.
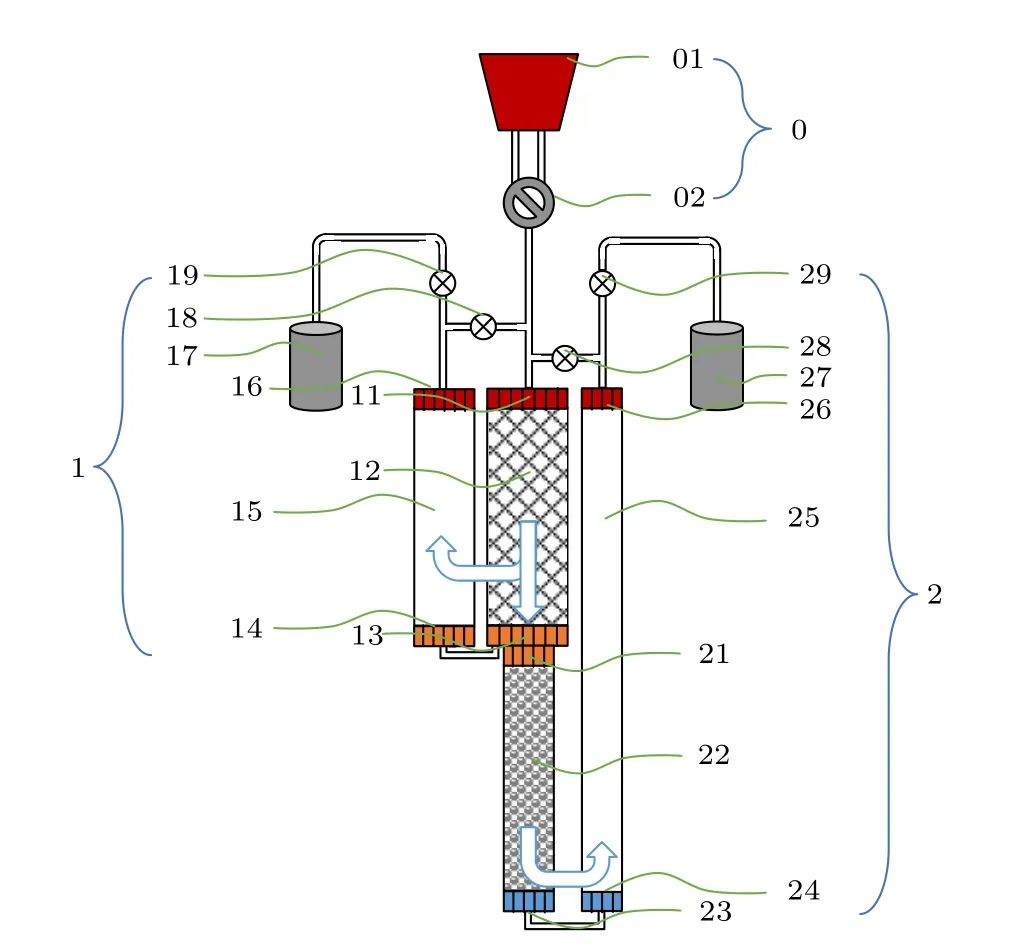
图1 双向进气型气耦合两级GM 脉冲管制冷机结构示意图Fig.1.Schematic of the two-stage gas-coupled double-inlet GM type pulse tube cryocooler.
本文制冷机主要采用“双向进气+小孔气库”的气耦合两级制冷流程,即从压缩机输送来的工质气体被分成3 部分,一部分直接流向第1 级回热器,另外两部分依次流向第1 级和第2 级双向进气.流向第1 级回热器的工质气体再被分成两部分,一部分经过第1 级脉冲管流向脉管热端完成基本的热力学循环,另一部分直接流向第2 级回热器,再经过第2 级脉冲管最终流向脉管热端.表1为本文所研制的4 K 大冷量GM 型脉冲管制冷机的详细结构参数.

表1 4 K GM 型脉冲管制冷机主要结构参数Table 1.Main structural parameters of the 4 K GM-type pulse tube cryocooler.
3 数值计算及分析
图2 为预冷级和低温级小孔阀开度分别对两级制冷温度的影响曲线.从图2(a)可以看出,制冷机调相机构均关闭状态下,也即此时制冷机相当于基本型脉冲管,模型的最低温度仅有大约100 K.首先开启一级小孔,一级和二级制冷温度迅速降低.当一级小孔开度增至0.785 mm2,模型获得30 K 左右的最低温度,此时一级的制冷温度接近40 K.继续增大一级小孔开度,一级和二级制冷温度均开始升高.保证一级小孔在最佳开度附近,逐渐开启二级小孔.从图2(b)可以看出,随着二级小孔开度的增大,二级制冷温度先降低后升高,而一级制冷温度逐渐升高.当二级小孔开度为0.385 mm2时,模型最低温度降低至13 K 附近,此时一级的制冷温度为55 K.
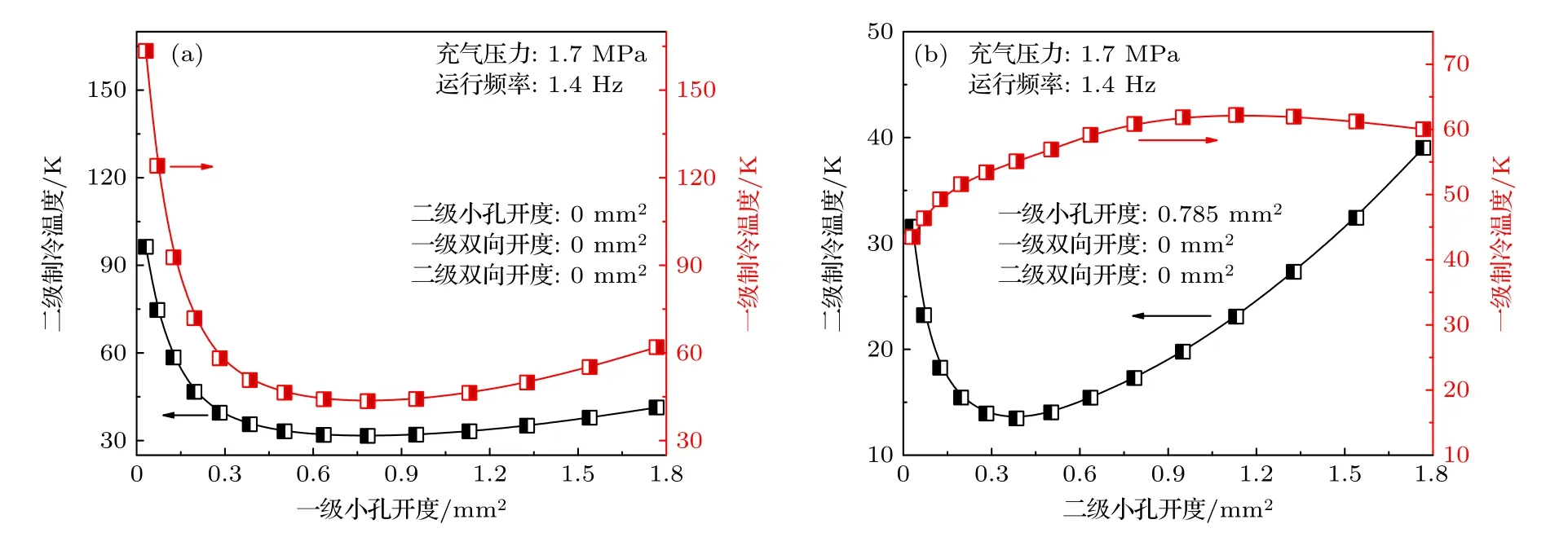
图2 一、二级小孔分别对一级和二级制冷温度的影响Fig.2.Dependence of the cooling temperatures of the two stages on the openings of the first-stage and the second-stage orifice valves.
图3 为预冷级和低温级双向进气阀开度分别对两级制冷温度的影响曲线.从图3(a)可以看出,同时保证一级小孔和二级小孔为最佳开度,逐渐开启一级双向,一级和二级制冷温度均先小幅降低后迅速升高,可见一级双向对降低最低温度影响甚微.保证一级小孔、二级小孔和一级双向为最佳开度,最后开启二级双向.从图3(b)可以看出,一级和二级制冷温度均先逐渐降低后再升高.当二级双向开度在1.131 mm2附近时,模型获得5.2 K 左右的最低温度,此时一级的制冷温度约为40 K.

图3 一、二级双向分别对一级和二级制冷温度的影响Fig.3.Dependence of the cooling temperatures of the two stages on the openings of the first-stage and the second-stage doubleinlet valves.
图4 为低温级双向进气阀中的直流量对两级制冷温度的影响曲线,负值表示直流方向从脉管热端指向冷端.从图4 可以看出,系统存在一定范围的负向直流可以进一步降低一级和二级的制冷温度.具体而言,所有阀门开度设定为最佳值,当二级双向中存在-0.005 g/s 的直流时,模型的最低温度可以从无直流时的5.2 K 进一步降低至2.7 K,此时的一级温度也可进一步降低至39 K.需要特别指出,这种直流只存在于具有双向进气等结构的流动回路系统中,由二阶压力梯度(时均压差)造成,在回路上处处相等,一定负向直流会改变制冷机沿程的温度分布,提高脉管的膨胀效率,减小冷端损失,这些均有利于提高系统的制冷性能[9,30].随着二级双向负向直流的进一步增大,计算模型已不再收敛.

图4 二级双向DC 直流对一级和二级制冷温度的影响Fig.4.Dependence of the cooling temperatures of the two stages on the DC flow rates caused by the second-stage double-inlet valve.
4 实验结果与讨论
基于上述理论模型和数值计算结果,设计并搭建了整套实验系统,如图5 所示,主要包括脉冲管制冷系统、压力波发生系统、充气及纯化系统、水冷系统、真空绝热系统以及数据采集系统等(图中只列出了部分).其中,压缩机采用Cryomech 公司的CPA1110 商业压缩机,充气压力为1.7 MPa,稳定后压比达到2.4.一级温度通过Lakeshore 公司生产的二极管温度计DT670-CU 进行测量,二级温度通过Lakeshore 公司标定过的CX-1030-CU-HT-1.4L 温度计进行测量,不确定度为5 mK.测量的温度通过Lakeshore 336 测量仪进行采集.压力通过昆仑海岸公司生产的型号为JYB-KO-HVG的压变式压力传感器进行测量,量程为0—4 MPa,准确度等级为0.5.测量的压力通过NI9203 板卡进行采集.制冷量通过热平衡法进行测量,所用直流电源型号为KEITHLEY 2220G,电压输出范围在0—30 V 之间,测量精度为1 mW.

图5 实验系统实物照片Fig.5.Photo of the experimental system with the cryocooler prototype.
图6 为本文所研制制冷机的降温测试曲线.可以看出,实验样机在1.7 MPa 充气压力和1.4 Hz工作频率的运行工况下,整个降温过程中二级冷头降温速度始终快于一级冷头.在开机1 h 后,二级冷头的制冷温度即可降低至20 K 以下,此时一级冷头的制冷温度为125 K.在开机大约3 h 后,二级冷头的制冷温度稳定在3.1 K,此时一级的制冷温度接近45 K.二级冷头降温速度快于一级冷头,表明制冷机目前一、二级气量分布不合理,仍存在较大的优化空间.一级制冷温度较高,可能原因是一级冷头质量较大,热量交换不充分,冷头测量温度远高于内部气体温度.图7 为所研制制冷机在不同温度的制冷量测试曲线,该制冷机可以在4.2 K 提供大约0.8 W 制冷量.
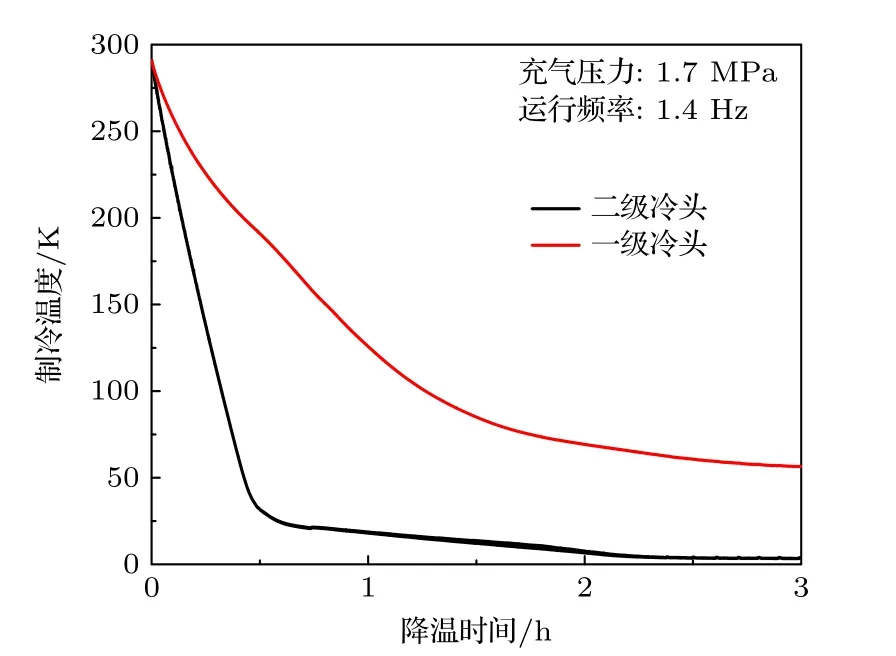
图6 制冷机样机典型降温曲线Fig.6.Time-dependent temperature distributions of the cryocooler prototype.

图7 制冷机样机不同温度下的典型制冷量Fig.7.Tested cooling power of the cryocooler prototype at different temperatures.
图8 为所研制制冷机在不同位置的压力数据测试曲线.从图8 可以看出,系统虽然仍具有波动的特性,但也偏离了正弦波的特征,同时压力波也不近似于方波.具体而言,回热器入口高压达到2.1 MPa,低压达到1.0 MPa,压差达到1.1 MPa,压比达到2.1.两级气库入口压力均在1.53 MPa附近小幅波动,系统平均压力低于充气压力是因为此时制冷机稳定工作在4 K.
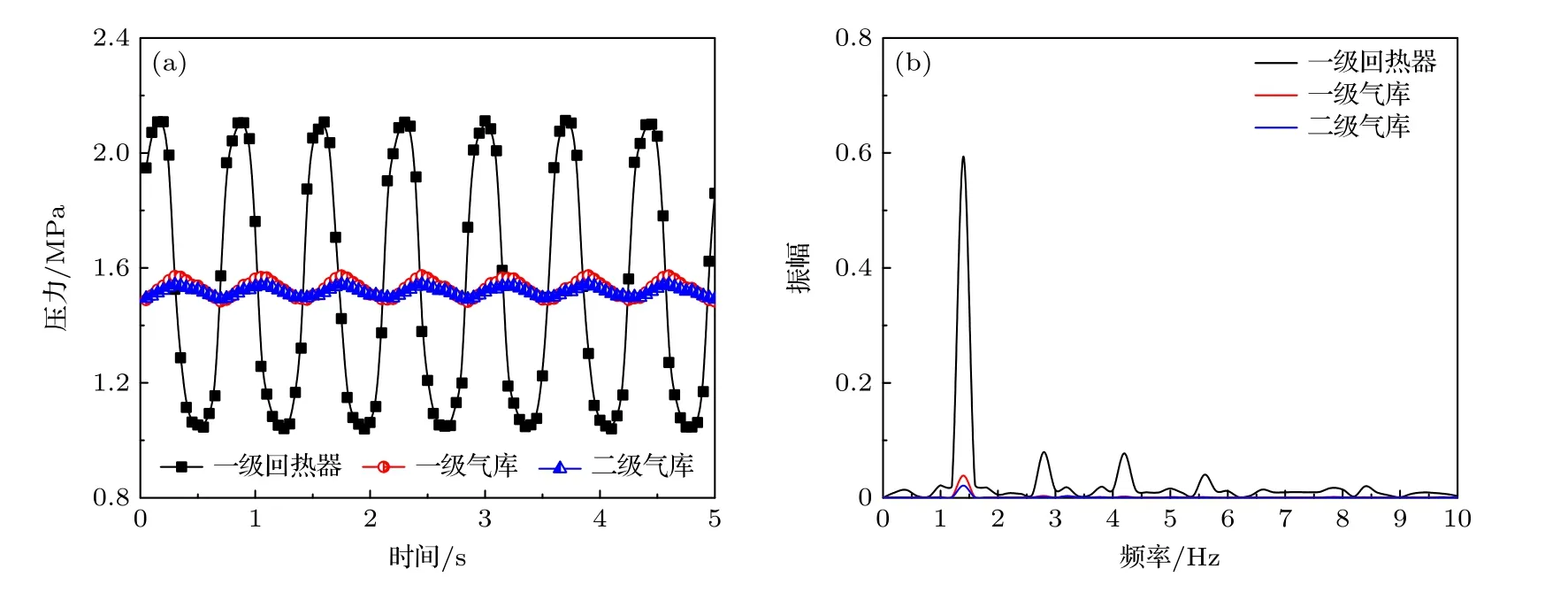
图8 制冷机样机不同位置压力波动 (a)实时数据;(b)傅里叶分析Fig.8.Tested pressure oscillation of the cryocooler prototype at different positions: (a) Real-time data;(b) Fourier analysis.
图9 为实验过程中相位调节和直流调节对制冷机样机性能的影响.一、二级小孔阀和一、二级双向阀采用自主设计的针阀,并与系统热端耦合在一起.实验中定量测量双向进气直流比较困难,为了定性控制直流方向,在回热器入口和气库入口之间增加了一条回路,通过使用单向阀、针阀组合来额外引入固定流向的直流(已有实验验证了该方案对直流控制的可行性[8,10,31]).此外,实验过程中还同时监测一、二级回热器和一、二级脉冲管中间位置的温度变化,以此来辅助判断制冷机调节对系统内部造成的影响.如图9(b)所示,二级回热器中间温度对相位调节反应较为敏感,实验过程中调节4 个阀门开度需要保证此温度稳定在46 K 以下,二级冷头即可获取4.2 K 以下的制冷温度;二级脉冲管中间温度对直流方向调节反应敏感,当制冷机中存在大小和方向合适的直流,此温度几乎不变且稳定在31 K 附近,此时二级冷头获得3.1 K 的最低温度.一旦引入反方向直流,二级脉冲管中间温度将有可能升高至100 K 以上,此时制冷机已无法获取液氦温区温度(图9(b)未显示).
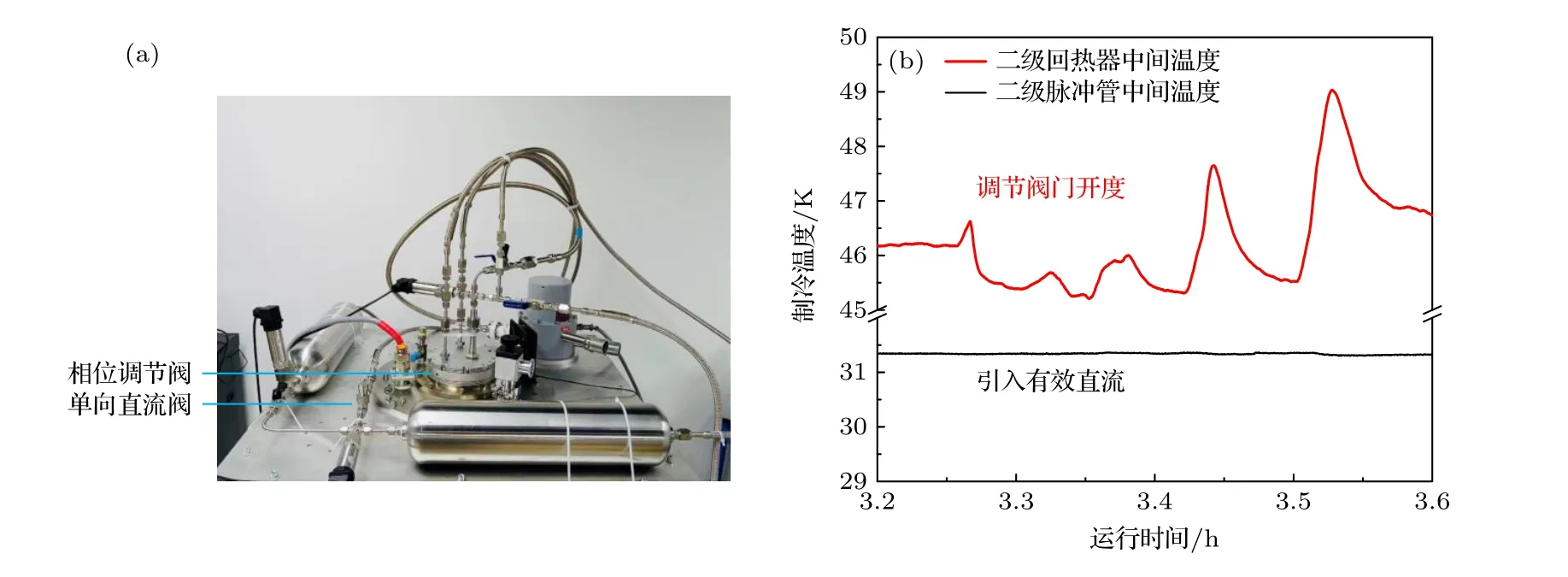
图9 制冷机样机相位调节和直流调节的影响 (a)实物照片;(b)温度波动Fig.9.Effects of phase shifting and DC flow on the cryocooler prototype: (a) Physical photo;(b) temperature fluctuation.
表2 对比了本文所研制制冷机与国际主流产品在液氦温区的性能.目前该制冷机最低温度已经接近国外同类水平,但降温时间和4.2 K 制冷量仍与国外存在一定差距.分析以上实验数据可能的原因主要有一级冷头降温过慢(一级冷头质量达到了3.4 kg)、温度过高和回热器入口压比较小,因此后续的性能优化实验主要集中在一级冷端换热器的结构设计与优化、压缩机与制冷机的阻抗匹配特性研究以及系统两级气量分配特性研究等方面.
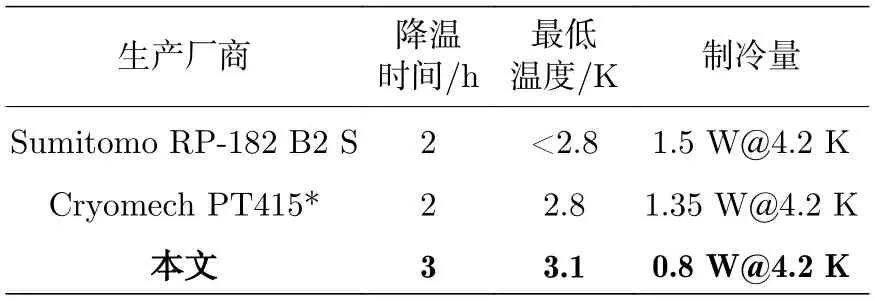
表2 与其他同类主流制冷机产品比较Table 2.Comparison with mainstream products of 4 K GM-type pulse tube cryocoolers.
5 结论
针对液氦温区GM 型脉冲管制冷机进行研究,构建了气耦合两级制冷机系统整机仿真模型,计算了预冷级和低温级调相机构分别对制冷机两级制冷性能的影响,分析了两级多个调相机构相互之间的耦合影响,研究了制冷机获取液氦温区温度的调节优化过程,并且研制了制冷机样机.相关结论如下:
1)制冷机两级调相机构均关闭状态下,模型最低温度仅有约100 K.依次优化一级小孔、二级小孔、一级双向和二级双向,模型最低温度可降低至2.7 K;
2)一级小孔、二级小孔和二级双向对降低低温级制冷温度作用明显,一级双向对降低低温级制冷温度影响甚微;
3)一级小孔和二级双向对降低预冷级制冷温度作用明显,一级双向对降低预冷级制冷温度影响甚微,二级小孔会恶化预冷级制冷温度;
4)研制的实验样机获得了3.1 K 的最低温度,在4.2 K 能够提供0.8 W 制冷量,或在8 K 提供5 W 制冷量,是目前国内公开报道的两级气耦合阀分离型GM 脉冲管制冷机的最好结果.
本文研制的原理样机制冷性能与国外主流产品还存在一定差距,未来计划从一级冷端换热器的结构设计以及压缩机与制冷机的阻抗匹配两方面进行改进以提高其制冷性能,进一步使用国产压缩机,并对制冷机内部的气耦合特性展开深入分析和研究.
感谢南方科技大学量子科学与工程研究院郑攀博士的讨论.
